基于模糊系统的散斑噪声滤波器
王 强,张合新,孟 飞,熊 鹏
基于模糊系统的散斑噪声滤波器
王 强,张合新,孟 飞,熊 鹏
(第二炮兵工程大学控制工程系,陕西 西安, 710025)
为了能有效滤除散斑噪声,提出了一种以模糊系统为基础的散斑噪声滤波器。这种滤波器包括了一个模糊推理系统,一个边缘检测和膨胀模块和一个图像合成器。模糊推理系统包括5个输入和1个输出,负责对散斑噪声图像进行滤波处理,其参数通过克隆选择优化算法训练优化得到。边缘检测和膨胀模块用于区分图像的边缘区域和光滑区域,图像合成器则是根据边缘检测和膨胀模块获取的信息分区域对滤波输出图像进行合成。文中将该方法与其他几种常用的散斑噪声滤除方法进行了比较,实验结果表明,与其他方法相比该方法可以显着减少图像的散斑噪声,同时保留边缘、细节等有价值的信息。
散斑噪声滤波器;模糊系统;图像处理
0 引言
成像系统在获取图像过程中会受各种干扰因素的影响,噪声则是最常见的干扰因素。在信号和图像处理领域有很多噪声模型以及不同噪声对于图像质量的影响分析。其中有一种是散斑噪声模型,这是一种乘性噪声。在这种模型中,图像质量被降低是因为图像中得到的像素值被乘以了噪声分量。合成孔径雷达,超声波、激光等成像系统都会受到散斑噪声的影响。在这些系统中,散斑噪声的产生是物体表面反射信号干涉产生的结果。在最后得到的图像中几乎所有的像素都会受到该噪声的影响,最终导致的结果便是图像中产生整块的斑纹以致于降低了图像的信噪比和分辨率。一些常用的散斑噪声滤波器的目的在于滤除噪声的同时不丢失有用的信息,保留边缘等的有价值的细节。
在此之前,已经有很多用于散斑噪声滤除的方法已经被提出。其中基于图像的局部统计滤波的Lee方法,基于同态映射的同态滤波,小波软阀值算法和基于数学形态的多方向形态滤波及其它们的改进型是最常见的方法[1]。在噪声图像中,细节或边缘与噪声之间的区别并不明显。这种信息的不确定性和不完整性给滤波操作带来了困难,而模糊理论正好能适应这些非确定性,因此在图像滤波过程中应用模糊理论可以取得较好的噪声去除效果[2]。近年来一些以模糊逻辑为基础的方法被提出用于噪声滤除。例如:F. Russo等提出了FF方法,将模糊系统理论应用于图像滤波。罗海驰等提出了一种基于自适应神经模糊推理系统[3]用于滤除椒盐脉冲噪声。而本文提出了一种以模糊推理系统为基础的散斑噪声滤波器。实验结果表明,本文所提出的滤波器能有效滤除散斑噪声,而且能够很好保护边缘、细节等信息。
1 散斑噪声基本性质及常用滤除方法
1.1 散斑噪声基本性质
为了能够更好地去除散斑噪声,首先对散斑噪声的性质进行分析研究。散斑噪声可以近似为一种乘性噪声,具有负指数分布特性[4]。可以用如下的噪声模型来近似表示:
=0×sn(1)
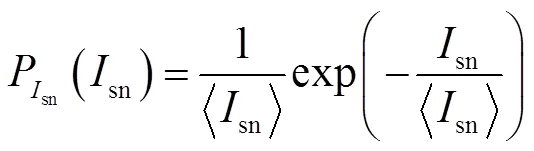
式中:为接收到的信号强度,通过图像中的像素灰度值来体现;0是理想无噪声信号强度,它反映的是目标的真实信息;sn是散斑作用系数;áñ表示求平均值。
1.2 常用的散斑噪声去除方法
1.2.1 同态滤波
在前文中提到,散斑噪声是一种乘性的非线性噪声,乘性噪声存在的一个问题就是它与信号的相倚性比较强,而同态变换可以使被乘性噪声污染的信号实现信噪分离,使乘性噪声转变成为加性噪声,削弱噪声与信号的相倚性[5]。同态滤波方法就是首先对信号进行同态变换,然后用一种合适的线性滤波器抑制噪声,最后进行逆变换,恢复信号。由于在进行滤波的时候采用的是一种线性滤波器,势必会造成图像边缘和细节上的模糊和缺失。
1.2.2 局部统计滤波
局部统计滤波算法由Lee J. S.提出所以这算法又叫Lee滤波器[6]。Lee滤波器假定像素的采样均值和变差等于其邻域的局部均值和变差,并且将图像的强度函数用泰勒展开,取其一阶使其线性化,然后根据最小平方误差估计在被散斑噪声污染信号中获得逼近信号。它的实质就是用一个线性函数来逼近一个非线性函数,用这种方法处理后肯定会造成图像边缘的模糊。
Lee滤波算法可以用下式来表示:
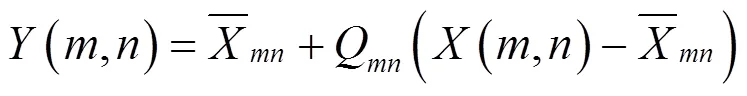
式中:(,)是滤波器逼近的结果;(,)是含噪图像信号。
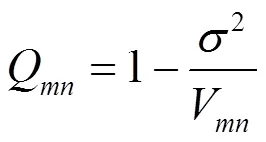
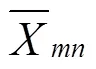
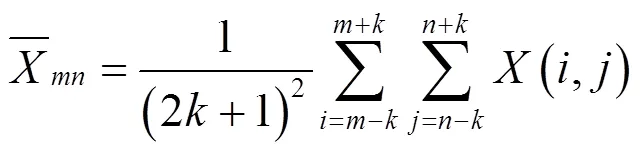
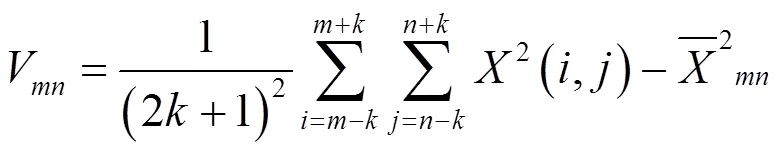
1.2.3 小波阈值算法
小波变换是继傅里叶分析之后另一种有效信号分析工具,它的实质在于减小以至于完全剔除由噪声产生的系数,同时最大限度地保留有效信号产生的系数,再由处理后的小波系数重构原信号,获得原信号的最佳估计。小波阈值算法主要分为以下3步[7]:
①应用Mallat算法对信号进行分解:选择合适的基小波,并确定尺度,然后进行小波分解。
②阈值法修正小波系数:对每一尺度选择适当的阈值,并按一定的策略,对其尺度Mallat算法对信号的分解的系数进行
③信号重建:通过小波逆变换,利用原信号尺度的近似和经阈值处理后的小波系数重建原信号。
2 模糊推理系统
在本文所提出的方法中使用的模糊推理系统是一个5输入单输出的一阶Sugeno模糊模型,对于它的输入选择了广义钟型隶属函数,输出则选用了线性函数。这个模糊推理系统包含了10条规则,其模糊规则集如下:
① if (1Î11)&(2Î12)&(3Î13)&(4Î14)
&(5Î15)
then1=111+122+133+144+155+16
② if (1Î21)&(2Î22)&(3Î23)&(4Î24)
&(5Î25)
then1=211+222+233+244+255+26
③ if (1Î31)&(2Î32)&(3Î33)&(4Î34)
&(5Î35)
then1=311+322+333+344+355+36
……
⑩ if (1Î101)&(2Î102)&(3Î103)&(4Î104) &(5Î105) then1=1011+1022+1033+1044+1055+106(7)
式中:X是模糊系统的输入;Q表示系统根据第条规则得到的输出;d,是结论参数;M,表示第个输入的第个隶属函数。对于输入X,定义的广义钟型隶属函数描述如下:
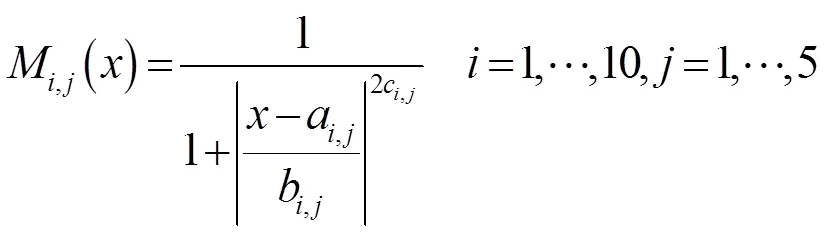
式中:a,,b,,c,为前提参数,它们和d,一起确定隶属函数的形状,这些参数在训练过程中不断优化,关于训练过程这将在后面进行说明。
模糊推理系统的输出等于各Q的加权平均:
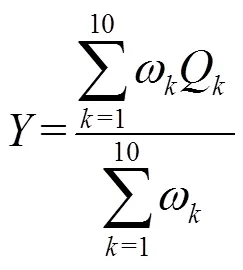
式中:加权系数表示第条规则的激励强度,的计算方法如下:

3 克隆选择优化算法
克隆选择优化算法(Clonal selection optima- zation algorithm,CSOA)的思想灵感来自于人类免疫系统的克隆选择原理,它能够在寻求全局最优解的过程中避免陷入局部最优的求解,在求解具有多模态性质或时变性质的优化问题中能够很好的体现CSOA的这一优势[8]。因此,CSOA正被广泛的应用于工程实践中。CSOA的原理程序框图如图1所示。
初始种群随机产生,待求解的问题由抗原表示,可行的解由抗体表示。在算法中根据抗体和抗原的亲和度对抗体进行排序,然后根据亲和度不同按不同比例进行克隆。克隆数量的计算方法如下:
C=round(/) (11)
式中:是克隆系数;是可行解的排序号。从式(1)中可以看出克隆的数量与亲和度有关,亲和度越高复制数量越多,反之则越少。于此相反的是:当抗体的亲和度较高时抗体的变异就小,当抗体的亲和度较小时,抗体的变异就大。最终这些抗体将被重新评估与抗原的亲和度,最合适的抗体将出现在下一代群体中。这个循环直到达到终止条件时才会停止。
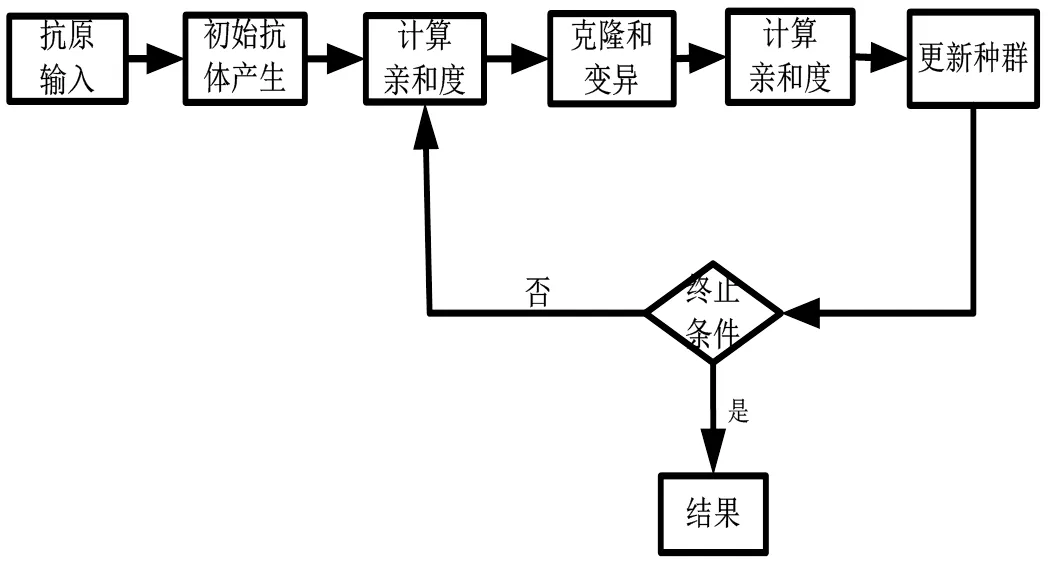
图1 CSOA原理程序框图
4 模糊滤波器
前文中所提到的模糊推理系统通常作为像小波变换这种以模糊逻辑为基础方法的一部分出现。在这些方法中模糊推理系统通常被用于系数的调整与优化。但是单独一个模糊推理系统也可以用于数字图像的噪声滤波只要为它提供训练所需的图像。在模糊推理系统参数被准确找到的前提下,一旦模糊推理系统通过训练,只要一个简单优化算法就可以使系统输出的图像与没有噪声影响的图像几乎没有什么差别。然而模糊推理系统的参数确定十分困难,在许多情况中,在有一些微小误差的情况下也是能得到很不错的去噪效果的。
4.1 模糊推理系统的训练
模糊推理系统输入与输出之间的关系由用于输入的隶属函数决定。在系统的训练阶段,通过所提供的训练数据可以训练得到决定模糊规则的隶属函数的系数。本文模糊滤波器中的模糊系统的参数则通过CSOA进行优化。训练的步骤如图2所示,当训练完成时输出的图像无限趋近于原始的无噪图像。
本文所提出模糊滤波器使用的模糊推理系统有5个输入和1个输出。模糊规则库包含了10条规则,对于模糊系统规则库的数量可以进行试探性的实验,它可以是大于或小于10。实验结果表明,增加规则的数量可以略微提高所提出的模糊滤波器的性能,但同时也增加了训练的时间以及该系统的复杂性。因此,在决定规则的数量时应尽量平衡系统性能和系统的复杂性之间的关系。
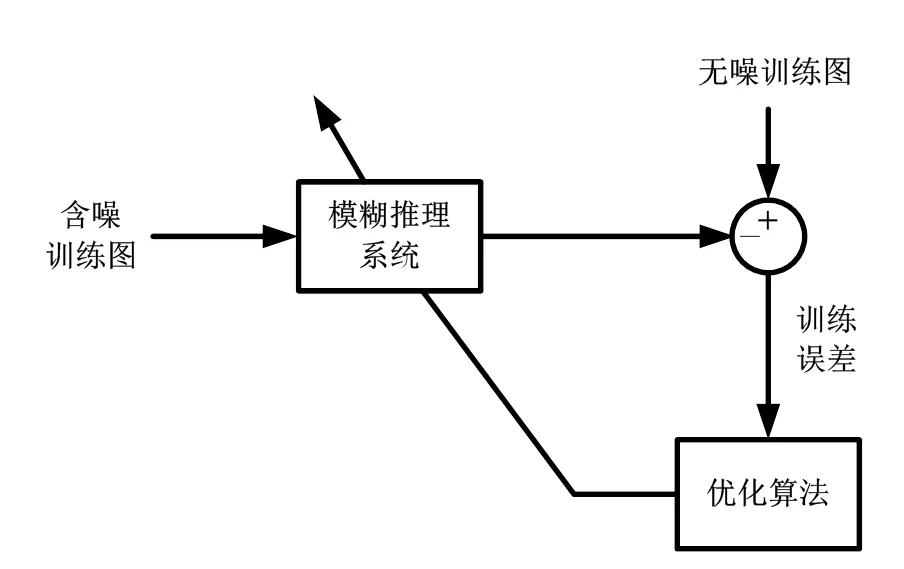
图2 模糊系统训练
当前以模糊滤波器为基础的方法已经成功地应用于数字图像的脉冲噪声的去除。脉冲噪声通常只会将整幅图像中的某些像素的像素值变为0或255,但是散斑噪声却能影响图像中某个区域内的所有像素。因此,合适训练图像对于构造一个用于散斑噪声滤除的模糊滤波器具有非常重要的作用。训练图像必须同时包含含有不同灰度值的光滑的区域和边缘区域。因此,训练图像可以通过在各种人造的无噪声图像上添加散斑噪声来获得,当模糊系统通过这些图像训练后,它就可以用于各种散斑图像的滤波。
图3(a)和3(b)所示的图像就是在计算机中生成的用于训练的图像。图3(a)是一幅无噪训练图,尺寸是120×120像素,其中的每个小方块大小是8×8像素,每个小方块中的像素值都相同随机均与分布于0和255之间。含噪训练图3(b)则是在无噪图像上添加了方差为0.04的散斑噪声后得到的。噪声方差值对于模糊系统的训练不是十分关键,但是根据以往的实验经验可知,当输入的含噪图像的噪声方差接近于训练图像的噪声方差时才能得到最优的滤波结果。在通常情况下不可能知道要处理图像的噪声方差,所以训练图像的方差大小的选取全凭经验,不能选太大或太小[9-11]。

图3 训练图
在使用训练图像对系统进行训练的时候选择了一种特定的邻域。这种特定的像素邻域在滤波窗口中的形式如图4(a)中所示,它的应用方法则表示在图4(b)中。其中TN作为模糊系统的输入从含噪训练图像中获取,系统输出用TO表示。在邻域的选择上不止本文中所示的这一种方法,但是实验结果表明:使用本文的邻域选取方法是本文滤波器能达到最好的效果。

图4 滤波窗口及其应用
4.2 本文滤波器
作为一种噪声滤波器,在使用的过程中最容易出现的问题就是滤波造成图像的边缘模糊。在滤波处理中光滑区域受的影响往往较小,然而在边缘和细节处有可能会产生信息丢失或者边缘畸变,最终导致的结果就是图像的理解性变差和解释性变得复杂[12-13]。如果要想获得好的滤波效果,那么滤波器就必须对边缘和细节信息十分敏感。
本文所提出的滤波器的结构如图5所示。在通常情况下,通过训练的模糊滤波器可以满足对散斑噪声的滤波需求,但是为了提高滤波器的性能,模糊系统采用了一种级联方式。这样处理的结果是:光滑区域更加平滑,但是与此同时细节和边缘区域也被平滑处理了。为了避免边缘平滑的发生,在滤波器中加了一个边缘检测和膨胀模块,该模块中获取到的信息将用于最后的图像复原。
4.2.1 边缘检测与膨胀模块
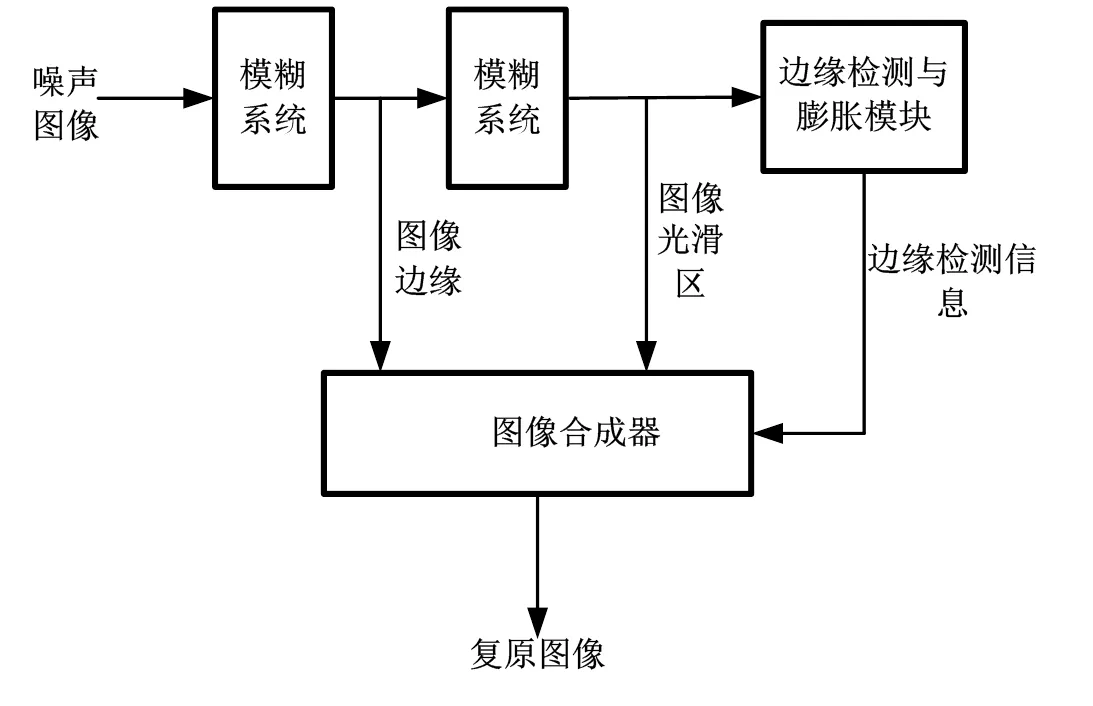
图5 本文模糊滤波器
在数字图像中通过边缘算子可以很容易地检测出一幅图像的边缘区域,但是在一幅被噪声污染的图像中就不是那么容易了,因为噪声会在图像中产生一些伪边缘[14-15]。在本文滤波器中,在图像进入边缘检测与膨胀模块之前已经滤除了散斑噪声的影响,所以只要一些简单的边缘检测算子就可以很容易地检测出图像的边缘。在这里选用Sobel算子作为边缘检测算子。
图像的膨胀处理是为了检测出图像的边缘附近的区域,而且在本文方法中要对边缘图像要进行两次的膨胀处理,并在边缘附近标记出3×3像素大小的膨胀区。经过这样处理后图像整体被分成了3个部分:边缘区域、边缘过渡区、光滑区。
4.2.2 图像合成器
图像的边缘及其膨胀处理后的信息将用于图像的复原。图像的边缘区域的像素值由第一次滤波输出图来确定,而边缘过渡区的像素值则用两次滤波后的输出图来确定。在膨胀区之外的光滑区像素值则通过计算两张滤波处理后的输出图的均值来确定。从像素值的计算方法上来看,一次滤波输出的对第一次膨胀区域贡献更大,两次滤波的对输出对第二次膨胀区域贡献更大。实验结果表明通过这样处理模糊滤波器的性能能有很大提升。
5 实验结果及分析
为了验证本文中所提出的模糊滤波器的性能,采用一些常用的、人为加入散斑噪声的标准数字图像作为测试对象。在测试中选用了3张不同的图像(Lena,Bridge,Boats),每张图像中又加入了均值为零但是方差不同的3种散斑噪声。
为了验证该滤波器的性能将它与现在国内外使用效果较好的滤波方法进行对比,包括了最小均方误差Lee滤波器(Minimum mean squared error Lee filter,Lee MMSEF),Frost滤波器(Frost filter,FROSTF),ADF滤波器(Anisotropic diffusion filter,ADF),SRADF滤波器(Anisotropic diffusion speckle noise removal filter,SRADF),图像平滑Lee滤波器(Image smoothing Lee filter,Lee ISF),中值滤波器(Median filter,MEDF)和均值滤波器(Mean filter,MF)。而比较的标准主要是噪声的滤除效果,和滤波器对边缘及细节处的保护能力。滤波器对噪声的滤除效果肉眼可以很明显得看出来。至于边缘和细节保护能力选用均方误差(Mean Squared Error,MSE)作为评价参数[16]。
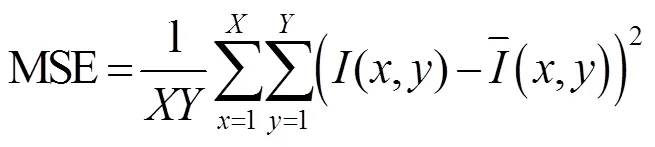
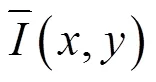
图6中(a)~(j)分别是标准图、噪声方差为0.04的未经处理的图、均值滤波图、中值滤波图、Lee MMSEF滤波图、FROSTF滤波图、ADF滤波图、SRADF滤波图、Lee ISF滤波图和本文方法滤波图。首先我们从散斑噪声滤除效果上将本文方法与其他方法来进行对比分析。从以上几张图中可以看到图(c)、(d)、(f)、(g)中还明显存在散斑噪声,说明均值滤波、中值滤波、FROSTF滤波、ADF滤波这几种方法对散斑噪声的滤除能力较弱,从功能上来说就不能满足实际应用的需要。在考虑了滤波效果之后要对剩下的几种滤波器在边缘和细节的保护能力上来进行对比分析。其中,图(h)的边缘和细节非常模糊,而且在处理完之后整幅图像颜色偏暗。图(i)的整体效果还可以,但是与图(j)相比,在人物的面部细节上与帽子的轮廓上它的模糊感觉更加明显。相比之下图(e)和图(j)的效果最好,也就是说在处理方差为0.04的散斑噪声时Lee MMSEF滤波器和本文提出的滤波器效果最好。
为了更加直接地说明各个滤波器对图像边缘及细节的保护能力,同时也为了试验这些滤波器对图像噪声是不是具有选择性,本文对选用的3张标准图片分别加入了标准差为0.01,0.04和0.07的散斑噪声,然后计算每种滤波器对这9张图处理后的MSE值,最后利用这些数据分析各个滤波器的性能。结果如表1和表2所示。

从表1和表2中可以看出本文提出的滤波器在边缘和细节的保护上相比于其他几种滤波器做得更好。在上文中提到当散斑噪声方差为0.04的时Lee MMSEF滤波器和本文提出的滤波器效果都比较好,但是从表中数据可以看到当方差为0.01和0.07时Lee MMSEF滤波器的性能就明显不如本文算法了,这说明了本文提出的滤波器对噪声没有选择性。综上所述,从对噪声滤除的效果和边缘、细节信息保护这两方面来看本文提出的滤波器的性能更加全面、稳定。
6 结束语
本文提出了一种以模糊系统为基础的散斑噪声滤波器。该滤波器首先通过模糊推理系统实现对含噪图像的去噪处理,然后用边缘检测和膨胀模块区分图像的边缘和平滑区,最后根据区分的不同区域在图像合成器中采用不同的方法实现图像合成、复原。其中的模糊推理系统的参数通过人工构造的计算机图像进行训练,克隆选择算法优化得到。由实验结果可知,与其他滤波器相比该滤波器在有效滤除散斑噪声的同时可以很好地保护图像的边缘、细节等重要敏感信息。
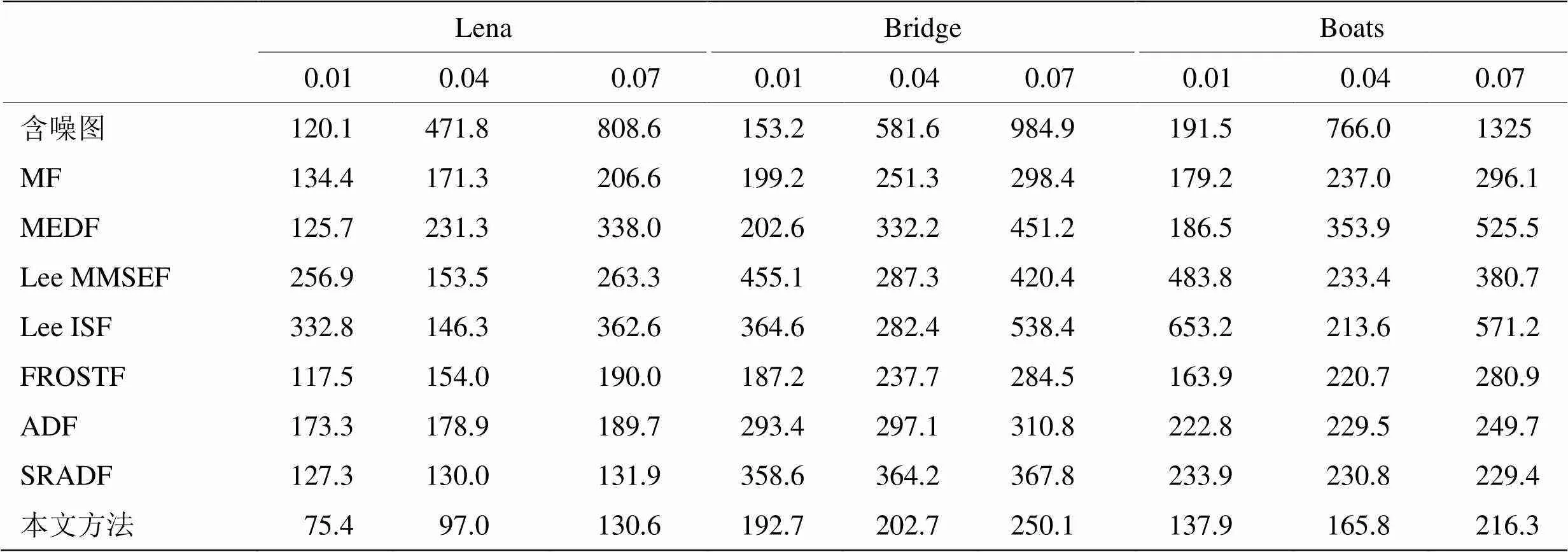
表1 Lena、Bridge和 Boats滤波处理后的MSE值
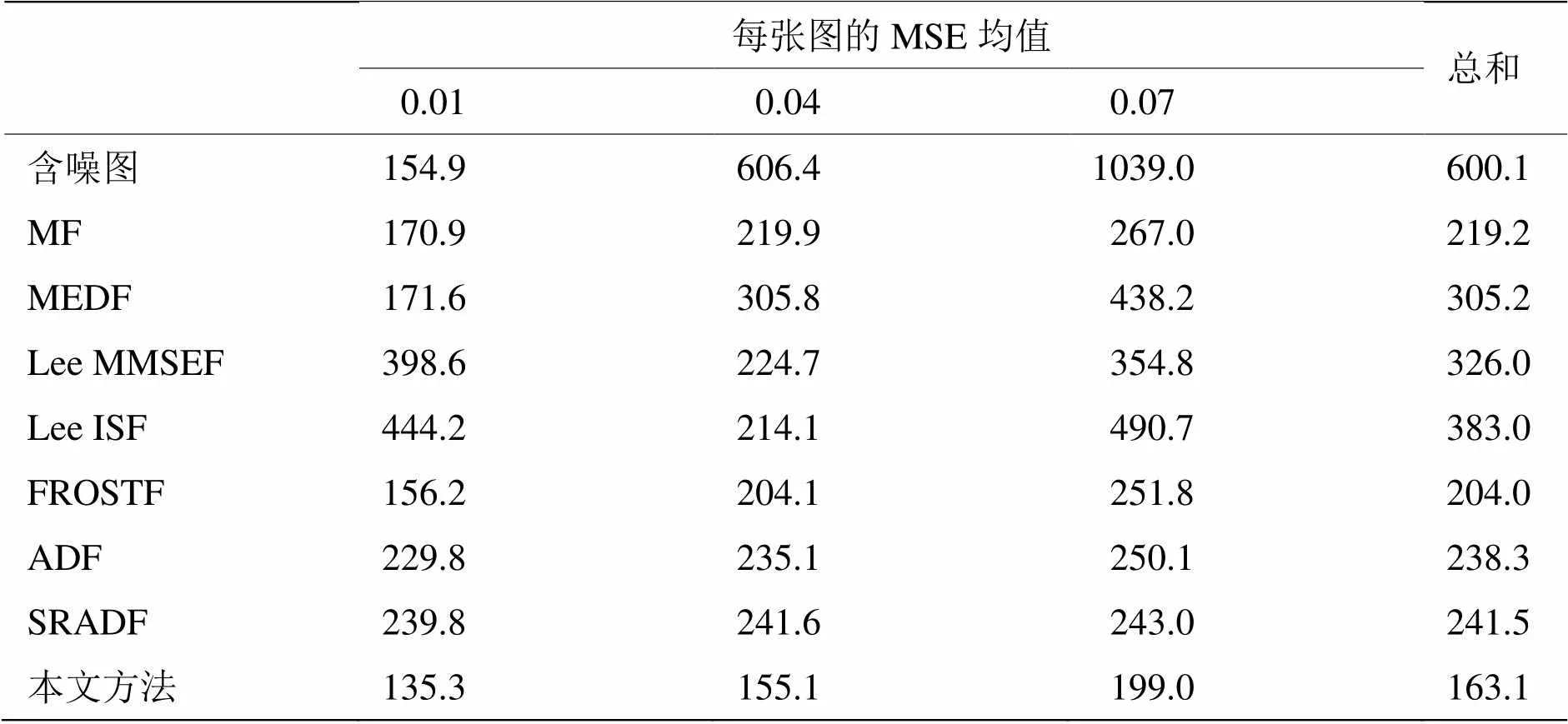
表2 滤波输出图的MSE均值
[1] 蒋立辉, 赵春晖, 王骐. 散斑噪声抑制算法比较研究[J]. 激光与红外, 2002, 32(6): 431-434.
JIANG Lihui, ZHAO Chunhui, WANG Qi . Study and comparison of speckle noise suppressing algorithms[J]., 2002, 32(6): 431-434.
[2] 朱立新, 杨扩, 秦加合. 一种新的基于自适应神经网络模糊推理系统的图像滤波器[J]. 计算机科学, 2014, 41(6): 211-214.
ZHU Lixin, YANG Kuo, QIN Jiahe. New noise digital images filter based on adaptive neuro-fuzzy nnference System[J]., 2014, 41(6): 211-214.
[3] 罗海驰, 李岳阳, 孙俊. 一种基于自适应神经模糊推理系统的图像滤波方法[J]. 计算机科学, 2013, 40(7): 302-306.
LUO Haichi, LI Yueyang, SUN Jun. Filtering method for images based on adaptive neuro-fuzzy inference system[J]., 2013, 40(7): 302-306.
[4] 李晓峰, 徐军, 罗积军, 等. 激光主动成像图像噪声分析与抑制[J]. 红外与激光工程, 2011, 40(2): 332-337.
LI Xiaofeng, XU Jun, LUO Jijun, et al. Noise analyzing and denoising of intensity image for laser active imaging system[J]., 2011, 40(2): 332-337.
[5] LEE J S, WEN J H, AINSWORTH T L, et al. Improved sigma filter for speckle filtering of SAR imagery[J]., 2009, 47(4): 202-213.
[6] PUVANATHASAN P, BIZHEVA K. Interval type-II fuzzy anisotropic diffusion algorithm for speckle noise reduction inoptical coherence tomography[J]., 2009, 17(5): 733-746.
[7] ZHANG Y, CHENG H D, TIAN J, et al. Fractional subpixel diffusion and fuzzy logic approach for ultrasound speckle reduction[J]., 2010, 43(2): 2962-2970.
[8] 唐正, 胡珉. 空间自适应免疫克隆选择优化算法[J]. 计算机应用, 2009, 29(2): 561-564.
TANG Zheng, HU Min. Space self-adaptive inmune clonal selection optimization algorithm[J]., 2009, 29(2): 561-564.
[9] YUKSEL M E, BASTURK A.Application of type-2 fuzzy logic filtering to reduce noise in color images[J].2012, 56(7): 25-35.
[10] AMIRMAZLAGHANI M, AMINDAVAR H. A novel sparse method for despeckling SAR images[J].2012,50(4):5024-5032.
[11] HAJIABOLI M R. An anisotropic fourth-order diffusion filter for image noise removal[J].2011,92(8): 177-191.
[12] 王灿进, 孙涛, 陈娟. 基于像素点分类的激光主动成像混合滤波[J]. 中国激光, 2014, 41(3): 1-7.
WANG Canjin, SUN Tao, CHEN Juan. Hybrid filter based on pixel classification for laser active imaging[J]., 2014, 41(3): 1-7.
[13] ELAMVAZUTHI I, ZAIN M L B M, BEGAM K M. Despeckling of ultrasound images of bone fracture using multiplefiltering algorithms[J].2013,57(6): 152-168.
[14] HUANG B, BU P, WANG X, et al. Speckle reduction in parallel optical coherence tomography by spatialcompounding[J].2013,45(2): 69-73.
[15] ORTIZ S H C, CHIU T,FOX M D. Ultrasound image enhancement: a review2012, 25(3): 419-428.
[16] 韩红光. NSCT域红外图像改进非局部均值滤波算法[J]. 红外技术, 2015, 37(1) :34-38.
HAN Hong-guang. Improved non-local means infrared image filtering algorithm based on NSCT[J]., 2015, 37(2): 34-38.
A Novel Fuzzy Filter for Speckle Noise Removal
WANG Qiang,ZHANG Hexin,MENG Fei,XIONG Peng
(Department of Automation, The Second Artillery Engineering University, Xi¢an 710025, China)
In this paper, a novel fuzzy system-based filter for speckle noise removal is proposed. The proposed filter consists of a fuzzy inference system, an edge detection and dilation unit, and an image combiner. The fuzzy inference system includes 5 inputs and 1 output, and it is responsible for filtering the speckle noisy image. The edge detection and dilation unit is used for classifying the uniform areas and edge areas. The image combiner unites the output images according to the information coming from the edge detection and dilation unit. The training phase of the fuzzy inference system is implemented by using the clonal selection optimization algorithm with appropriate training data. The performance of the proposed method is compared with popular speckle noise removal filters available in the literature by performing extensive simulations. The experimental results show that the proposed method can significantly reduce the speckle noise from digital images while preserving edges, and valuable details.
speckle noise filtering,fuzzy inference system,image processing
TN751
A
1001-8891(2016)05-0415-07
2015-12-28;
2016-02-29.
王强(1993-),男,硕士研究生,主要从事激光主动成像及目标识别方向研究。E-mail:15158001096@163.com。
国家自然科学基金(61203189)。

