关于Hermite矩阵Schur补的迹的几个不等式



关于Hermite矩阵Schur补的迹的几个不等式

引文格式： 解运运,段复建.关于Hermite矩阵Schur补的迹的几个不等式[J].桂林电子科技大学学报，2016,36(1):79-82.

解运运，段复建

(桂林电子科技大学 数学与计算科学学院，广西 桂林541004)

摘要：利用Schur补的理论知识和Hermite矩阵的迹的不等式，研究了Hermite矩阵Schur补的迹的不等式的遗传性质，得到了Hermite矩阵Schur补的迹的Minkowski不等式、Holder不等式以及其他形式的不等式，并给出了理论证明，为处理大规模的矩阵计算提供了理论支撑。

关键词：Schur补；Hermite矩阵；矩阵的迹

Schur补的概念[1]的提出大大地推动了数学领域的发展，大量工程问题可以归结为大规模的矩阵计算问题，而矩阵的Schur补是处理大规模矩阵计算的有效工具，在数值计算、矩阵理论、线性方程组求解、控制理论、统计分析等领域中有着重要的应用[2-7]。由于Hermite矩阵是一类特殊矩阵，它的迹作为矩阵的一个重要的数字特征也受到广泛的关注，文献[8-9]介绍了(半)正定Hermite矩阵的迹的几类不等式，但对于Hermite矩阵Schur补的迹的遗传性质的研究较少。为此，研究不同条件下Hermite矩阵Schur补的迹，得到了Hermite矩阵Schur补的迹的Minkowski不等式、Holder不等式等其他形式的不等式，并给出了理论证明，为求解大型Hermite矩阵计算提供了理论依据。

1基础知识

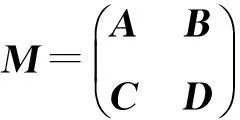
M/B=C-DB-1A；

M/C=B-AC-1D；

M/D=A-BD-1C。

定义2设A∈Cn×n，若AH=A，则称A为Hermite矩阵，记为H(n)。

引理1[8]设A、B分别为n×m和m×n矩阵，则tr(AB)=tr(BA)。

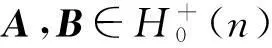
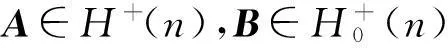
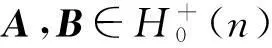
当B=μA，μ>0时等号成立。

当B=μA，μ>0时等号成立。

2主要结论及其证明

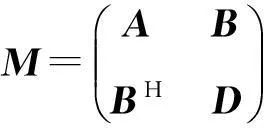
证明由题意知

根据Schur补的定义得

M/A=D-BHA-1B=D+BHB，

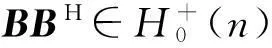
当且仅当D=μBHB，μ>0时等号成立。

证明由Schur补的定义得

M/A=D-BHA-1B，

tr(M/A)=tr(D-BHA-1B)，

由引理1和矩阵的迹的线性性质可知，

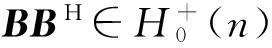
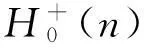
证明由Schur补的定义得：

M/A=D-BHA-1B，

tr(M/A)=tr(D-BHA-1B)。

由BHA-1∈Cm×n、B∈Cn×m、引理1和矩阵的迹的线性性质可知，

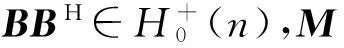
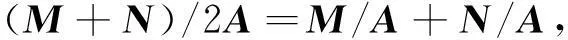
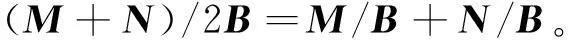
若将M、N推广到Hermite矩阵，结合定理2和定理3，可得2个Hermite矩阵和的Schur补的迹的不等式。

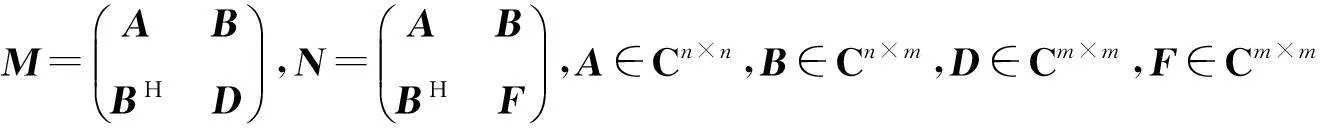
证明由定理2可知，

由(M+N)/2A=M/A+N/A得：

同理可得：

证明由Schur补的定义可知，

M/A=D-BHA-1B，

tr(M/A)=tr(D-BHA-1B)。

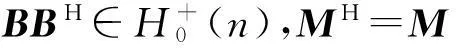
当D=0时，可得Hermite矩阵Schur补的迹的Holder不等式：

3结束语

在Schur补的理论基础上，通过对二阶分块Hermite矩阵的迹的研究，得到Hermite矩阵Schur补的迹的遗传性质，即Hermite矩阵Schur补的迹的Minkowski不等式和Holder不等式以及其他几种形式的不等式，这些不等式反映了Hermite矩阵Schur补的迹与原Hermite矩阵各子阵的迹的关系，可通过求解二阶分块Hermite矩阵的子阵的迹来判断Hermite矩阵Schur补的迹的上下界。

参考文献:

[1]SCHURJ.ÜberPotenzreihen,dieimInnerndesEinheitskreisesbeschränktsind[J].JournalfürdieReineundAngewandteMathematik,1917,147:205-232.

[2]PETRACG,ANITESCUM.ApreconditioningtechniqueforSchurcomplementsystemsarisinginstochasticoptimization[J].ComputationalOptimizationandApplications,2012,52(2):315-344.

[3]BARTLETTRA,BIEGLERLT.QPSchur:adual,active-set,Schur-complementmethodforlarge-scaleandstructuredconvexquadraticprogramming[J].OptimizationandEngineering,2006,7(1):5-32.

[4]GRIFFINGAR,LYNCHBR,STONEEA.AneigenvectorinterlacingpropertyofgraphsthatarisefromtreesbySchurcomplementationoftheLaplacian[J].LinearAlgebraanditsApplications,2013,438(3):1078-1094.

[5]GOWDAMS,SZNAJDERR.Schurcomplement,SchurdeterminantalandHaynsworthinertiaformulasinEuclideanJordanalgebras[J].LinearAlgebraanditsApplications,2010,432(6):1553-1559.

[6]JBILOUK,MESSAOUDIA,TABAK.SomeSchurcomplementidentitiesandapplicationstomatrixextrapolationmethods[J].LinearAlgebraanditsApplications,2004,392(15):195-210.

[7]LIUJianzhou,HUANGZejun,ZHANGJuan.ThedominantdegreeanddisctheoremfortheSchurcomplementofmatrix[J].AppliedMathematicsandComputation,2010,215(12):4055-4066.

[8]CHENHongqing.Severalinequalitiesofmatrixtraces[J].ChineseQuarterlyJournalofMathematics,1995,10(2):9-10.

[9]冯天祥.Hermite矩阵迹的几个重要不等式[J],数学杂志,2009,28(3):92-95.

[10]狄勇婧,段复建.矩阵和的Schur补的性质[J].桂林电子科技大学学报,2012,32(6):490-492.

编辑：曹寿平

Several inequalities about the trace of Schur complement of Hermite matrix

XIE Yunyun， DUAN Fujian

(School of Mathematics and Computational Science, Guilin University of Electronic Technology, Guilin 541004, China)

Abstract：By using the theoretical knowledge of Schur complement and the inequalities about the trace of Hermite matrix, the genetic properties of the inequalities about the trace of Schur complement of Hermite matrix are investigated. Minkowski inequality, Holder inequality and other inequalities about the trace of Schur complement of Hermite matrix are obtained and proved in the theory. They provide the theoretical support for dealing with the large-scale matrix calculation.

Key words：Schur complement; Hermite matrix; matrix trace

中图分类号：O151.21

文献标志码：A

文章编号：1673-808X(2016)01-0079-04

基金项目：国家自然科学基金(11461015)通信作者： 段复建(1965-)，女，黑龙江黑河人，教授，博士，研究方向为数值代数与最优化理论。E-mail:duanfj@guet.edu.cn

收稿日期：2015-07-08