一种改进阈值函数的EMD-CIIT语音去噪算法
一种改进阈值函数的EMD-CIIT语音去噪算法
引文格式: 钟金良,景新幸,杨海燕.一种改进阈值函数的EMD-CIIT语音去噪算法[J].桂林电子科技大学学报,2016,36(1):9-13.
钟金良,景新幸,杨海燕
(桂林电子科技大学 信息与通信学院,广西 桂林541004)
摘要:为了克服基于传统经验模态分解语音去噪算法在阈值去噪时阈值函数处理不平滑的缺点,对EMD-CIIT(EMD重复间隔阈值)语音去噪方法的阈值函数进行改进,并在Matlab平台搭建的语音识别系统进行仿真实验。实验结果表明,改进阈值函数的EMD-CIIT去噪算法具有较高的识别率及良好的鲁棒性。
关键词:语音去噪;EMD;改进阈值
语音信号是一种非线性、非平稳的信号。历年来,学者们一直致力于研究语音去噪的算法。基于谱减法的语音去噪方法假设语音信号短时平稳,其在实际应用中有一定的局限性[1]。1995年,Donoho在小波变换的基础上提出阈值去噪的方法[2],但基函数一经选定,整个分解和重构过程都已确定,无法再更改。文献[3-4]提出经验模态分解(empirical mode decomposition,简称EMD)算法。传统EMD算法将信号分解为一系列固有模态函数(intrinsic mode function,简称IMF)分量和一个残余分量,分解的各个IMF分量突出了数据的局部特征,残余分量则体现了信号变化趋势。受小波阈值去噪方法的启发,文献[5]提出了EMD重复间隔阈值(EMD clear iterative interval thresholding,简称EMD-CIIT)语音去噪算法,但其在间隔阈值上未考虑阈值选取的问题。为此,本研究对阈值函数进行改进,提出一种改进的EMD-CIIT语音去噪算法。
1经验模态分解原理
EMD算法是一种先进的信号处理方法,能有效处理非平稳、非线性的信号。分解的固有模态分量必须满足2个条件:1)零点数和极点数必须相等或至多相差1个;2)极大值和极小值组成的上下包络线关于时间轴局部对称,即上下包络均值为0。具体步骤为:假设原始信号为s(t),找出s(t)的所有极大值和极小值;依据极大值和极小值构造上下包络线;计算均值m11(t),求差值h11(t)=s(t)-m11(t);用h11(t)替换原始s(t);若h1,k-1与h1,k之间的差值小于设定值,则认为h1,k是一个IMF分量,记c1(t)=h1,k,r1(t)=s(t)-c1(t);再令s(t)=rn(t),直到rn(t)为常量或一个单调函数时,EMD分解结束,即得到原信号s(t)的分解式为
(1)
(2)
认为满足零均值的条件。其中ε为筛分门限,取值为0.2~0.3。
2基于EMD的去噪方法
对实测信号进行EMD分解,得到一系列IMF分量。对分解的IMF分量进行EMD直接阈值去噪(EMD direct-thresholding,简称EMD-DT),此方法的去噪思想类似于小波阈值去噪。EMD-DT方法的硬阈值函数为:
(3)
软阈值函数为:
(4)
其中Ti为i层IMF所用的阈值。为克服EMD-DT去噪不佳的缺点,利用Kopsinis等[5]提出的间隔阈值(EMD-IT)方法去噪。EMD-IT方法的硬阈值函数为:
(5)
软阈值函数为:
(6)

2专用式建筑学专业教室是通过一个单独的空间作为主要个体的教学空间类型,具有安静、封闭的空间特点,为学生进行独立的学习和思考提供了很好的空间。
(7)

3改进的阈值函数
由式(5)、(6)可知,当阈值大于极值点值,相当于在原来子波上与加权系数相乘[6]。用式(6)处理,发现其有间断现象,为使处理平滑,受文献[7]启发,提出一种改进的阈值函数。设计阈值函数为:
(8)

(9)
3.1改进阈值函数的奇偶性
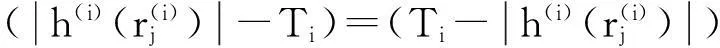
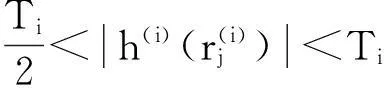
(11)

(12)
可见,改进的阈值函数为奇函数,函数关于原点对称,因此,只需分析阈值函数为正数的部分,另一部分可根据奇偶对称性得出。
3.2改进阈值函数的单调性
对函数F进行一阶求导,得
(13)
其中,α的取值范围为(0,1],又因j恒大于1,则1-j<0,可得一阶导数在整个区间上恒为正数,故改进后的阈值函数在区间上单调递增。
3.3改进阈值函数的连续性
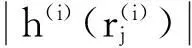
(14)

(15)

(16)
可见,改进的函数在阈值Ti处是连续的。

(17)

(18)
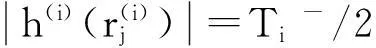
(19)
可见,改进的阈值函数在Ti/2同样也是连续不间断的。
分解得到的EMD分量为7层(j=7)时,调节系数α=0.88,改进的加权函数和软、硬阈值加权函数的函数图形如图1所示。

图1 不同阈值对比Fig.1 The comparison of different thresholds
改进的阈值函数克服了硬阈值函数在间断点处不连续性及软阈值函数存在的恒定偏差问题。当子波极值大于阈值时,改进的阈值函数逐渐逼近硬阈值函数,而不像硬阈值函数不作改变。通过引入IMF分解层数j来减小加权子波与原始子波之间的偏差,使重构后得到的信号更加逼近原始信号。引入调节系数α目的是为了保证连续性,在实际应用中可根据具体情况,在(0,1]选取合适的α来提高硬阈值函数的逼近速度。
4改进阈值函数的EMD-CIIT语音去噪
当噪声较严重时,直接对第一个IMF分量进行多次随机改变,然后进行EMD-IT语音去噪,这种方法叫做重复间隔阈值语音去噪(EMD-IIT)。但当噪声较小时,直接对第一个IMF分量进行随机改变,会导致有用信号也包含在第一个IMF分量中,有用信号被一起滤除[9],改进阈值函数的EMD-CIIT语音去噪算法则可克服这一缺陷。算法步骤为:
1)对带噪语音进行EMD分解,获得IMF分量ci(t),i=1,2,…,L;对ci(t)进行传统的直接阈值去噪(EMD-DT),得到去噪后的IMF分量ci(t)。

步骤1)是利用小波阈值去噪的方法来处理带噪信号[10],然而,小波阈值去噪时,需要准确选取小波基函数。为此,利用EMD-DT进行噪声估计,由于IMF分量的第一个分量大部分由噪声构成[11],对其进行EMD-DT后可得到较好的噪声估计。
5仿真及结果分析
为了验证改进的EMD-CIIT算法的有效性和优越性,利用改进的EMD-CIIT算法处理不同信噪比的带噪语音信号。分别对未改进的EMD分解进行EMD-IIT语音去噪、改进算法的EMD-IT语音去噪、传统的EMD语音去噪和所提出的方法进行实验仿真。实验所用的语音信号来自NOIZEUS语料库,其采样频率为8 kHz,量化为16 bit。通过采集实际车载环境中的噪声,根据不同的信噪比(5、0、-5 dB)进行仿真实验,改进的EMD-CIIT算法去噪效果对比如图2所示。

图2 去噪效果对比Fig.2 The comparison of denoising effect
由图2可知,在不同信噪比下,特别是在信噪比为-5 dB时,改进的EMD-CIIT算法也有较强的语音还原能力。为了验证处理后的语音信号在语音识别系统的识别率,对“开窗”、“关窗”、“开灯”、“关灯”进行训练,分别设为[R0,R1,R2,R3],并对这些语音信号进行加噪,然后进行降噪处理,作为测试模板,最终识别结果为[T0,T1,T2,T3],其在Matlab界面显示如图3所示。
在不同信噪比下,分别对含噪声语音信号采用不处理、传统EMD多尺度法语音去噪、EMD-IT语音去噪、EMD-CIIT语音去噪、改进EMD-CIIT语音去噪进行处理,并分别计算出系统在不同情况下的识别率。计算识别率的公式为:
图3 识别过程Fig.3 Recognition process
其中:C为语音识别系统的识别率;N为语音库总的词汇数;H为正确识别的次数。不同算法的识别率对比如表1所示。从表1可看出,不同算法都可在语音识别系统上进行识别,但不同信噪比下识别率差距很大。经语音去噪处理后的语音识别率都有不同程度的提升,在信噪比较低的情况下,未处理的语音识别系统的识别率很低,传统的降噪算法对系统的识别率有所提高,但不很明显,改进的算法在提高语音识别系统的识别率上效果显著,即使在信噪比较低的情况下也有较大提高。

表1 不同算法的识别率
6结束语
为了克服传统基于经验模态分解语音去噪算法在阈值去噪时阈值函数处理不平滑的缺点,提出了一种改进阈值函数的EMD-CIIT算法,该算法可应用于语音识别系统中。较于其他传统算法,改进阈值函数的EMD-CIIT算法大大提高了语音识别系统的识别率。但本算法未考虑EMD在分解过程中产生的端点效应以及模态混迭的问题,这会使EMD分解过程中产生虚假分量,有待今后研究中加以改进。
参考文献:
[1]刘志坤,唐小明,朱洪伟.基于改进谱减法的语音增强研究[J].计算机仿真,2009.26(6):363-366.
[2]DONOHO D L.De-noising by soft-thresholding[J].IEEE Transactions on Information Theory,1995,41(3):613-627.
[3]HUANG N E,SHEN Z.The empirical mode decomposition and the Hilbert spectrum for nonlinear and non-tationary time series analysis[J].Proceedings of the Royal Society of London A,1998,454(1971):903-995.
[4]WU Z,HUANG N E.A study of the characteristics of white using the empirical mode decomposition method[J].Proceedings of the Royal Society of London A,2004,460:1597-1611.
[5]KOPSINIS Y,MCLAUGHLIN S.Development of EMD-based denoising methods inspired by wavelet thresholding[J].IEEE Transactions on Signal Processing,2009,57(4):1351-1362.
[6]李洋,景新幸,杨海燕.基于改进小波阈值和EMD的语音去噪方法[J].计算机工程与设计,2014,35(7):2462-2466.
[7]戴亮.非平稳噪声环境下的语音增强算法研究[D].长沙:中南大学,2012:31-36
[8]张雄伟,陈亮,杨吉斌. 现代语音处理技术及应用[M].北京:机械工业出版社,2003:111-124
[9]MANUEL B V,WENG B W,BARNER k E.ECG signal denoising and baseline wander correction based on the empirical mode decomposition[J].Computers in Biology and Medicine,2008,38(1):1-13.
[10]BOUDRAA A O,CEXUS J C.EMD-based signal filtering[J].IEEE Transactions on Instrumentation and Measurement,2007,56(6):2196-2202.
[11]曲从善,路廷镇,谭营.一种改进型经验模态分解及其在信号消噪中的应用[J].自动化学报,2010,36(1):67-73.
编辑:黎仁惠
An improved threshold function EMD-CIIT speech denoising algorithm
ZHONG Jinliang, JING Xinxing, YANG Haiyan
(School of Information and Communication Engineering, Guilin University of Electronic Technology, Guilin 541004, China)
Abstract:The threshold process of speech denoising method based on empirical mode decomposition is not smooth, so the threshold function of EMD-CIIT (EMD clear iterative interval thresholding) speech denoising algorithm is improved. A speech recognition system is built by Matlab simulation platform. The experimental results show that compared with other algorithms, there are higher recognition rate and good robustness in the improved threshold EMD-CIIT algorithm.
Key words:speech denoising; EMD; improved threshold
中图分类号:TN929.5
文献标志码:A
文章编号:1673-808X(2016)01-0009-05
通信作者:景新幸(1960-),男,湖北武汉人,教授,博士,研究方向为语音信号处理、非线性电路、集成电路设计。E-mail:jingxinxing@guet.edu.cn
基金项目:广西自然科学基金(2012GXNSFAA053221)
收稿日期:2015-03-23

