一种基于区域收缩的分布式声源定位方法
一种基于区域收缩的分布式声源定位方法
引文格式: 周利,刘庆华.一种基于区域收缩的分布式声源定位方法[J].桂林电子科技大学学报,2016,36(1):1-4.
周利,刘庆华
(桂林电子科技大学 信息与通信学院,广西 桂林541004)
摘要:为了提高分布式声源定位方法的定位精度,降低计算复杂度,提出一种基于区域收缩的分布式声源定位方法。该方法采用多个线性子阵列组成分布式定位阵列组,各线性子阵列根据时延定位法,分别估计声源的位置,并根据声源位置的估计值确定初始矩形搜索区域,结合极大可控响应功率,进行区域收缩获得声源的位置。仿真结果表明,该方法定位精度高,计算复杂度低。
关键词:分布式声源定位;区域收缩;搜索区域
分布式传感器声源定位技术广泛应用于视频会议、智能机器人等领域[1-2]。由于低成本、低功耗,该技术逐渐推广至人机接口、声源监控、智能家居等领域[3-4]。但是,分布式声源定位系统在节点计算能力、通信范围和能量存储等方面受限,且通常被安置于无人看守的恶劣环境中。因此,实现高精度定位、降低定位方法的计算复杂度具有重要的意义。
近年来,很多应用于分布式传感器网络的定位方法被提出。在含有混响条件的被动声源传感器定位系统中,可控响应功率-相位变换(steered response power with phase transform,简称SRP-PHAT)声源定位方法[5]具有较强的鲁棒性。其基本原理为:假设声源位置点,计算所有声源传感器之间接收信号的SRP值之和,然后在指定空间中搜索SRP值最大的点确定为声源的估计位置。该方法对布阵没有特定的要求,适用于分布式传感器阵列。但SRP-PHAT定位方法对整个视场空间进行搜索定位时计算量大,使得定位系统的能耗过大,不具实时性。为此,研究人员提出了多种改进的方法[6-7]。文献[8]提出了加权SRP-PHAT方法,该方法在SRP-PHAT方法的基础上,每个传感器的接收信号乘以权值,需要测量声源的指向性函数,给实际布阵带来很大困难。文献[9]利用混响效应来提高定位精度,但需要知道假设的声源位置点与阵元间冲激响应的先验知识。
为了在分布式定位系统中进行灵活布阵,减小定位方法的计算量,结合可控响应功率-相位变换声源定位方法,提出了一种基于区域收缩的分布式声源定位方法。
1信号模型与声源初步定位
1.1信号模型与时延求解
静态各向同性的近场声源信号s(n)在均匀、无损介质中传播,线性阵列中第i个全方位声传感器节点接收到的信号为:
(1)
其中:c为信号的传播速度;ri为传感器节点i与声源间的欧氏距离;ni为加性背景噪声。则阵列中节点i、j接收的信号的互相关函数ρij(τ)为:
(2)
假设各个传感器接收的信号之间、信号与噪声之间均不相关,得
(3)
对于宽带声源信号,当τ=0时,其自相关函数ρ(τ)取得最大值。因此,搜索互相关函数ρij(τ)的最大值,得到2个传感器节点间的时延为:
(4)
1.2单阵列初步定位模型
图1为单阵列初步定位模型,(xi,yi)为第i个传感器节点的位置,ri为声源(x0,y0)与节点i之间的欧氏距离。根据传感器节点间的时延tij,利用几何法[10]初步估计声源的位置参数。假设相邻传感器节点间的距离为l,则声源的位置参数为:
(5)
(6)
2初始搜索区域的确定方法
区域搜索定位算法对整个视场搜索定位的计算量很大[11-12],且容易陷入局部最优,无法得到全局最优解。为了减小搜索定位的计算量,采用多个线性传感器子阵列组成分布式传感器定位网络,对声源目标进行组合定位,分布式网络定位模型如图2所示。假设在整个定位视场中随机布设M个线性子阵列,子阵列的位置由其中心节点坐标以及子阵列相对于整个视场的参考方向的旋转角度α所确定。首先,各个子阵列并行对声源进行初始定位,得到声源的位置(xi,yi),i=1,2,…,M,在图2中采用星号*表示。其次,对于M个可能的声源位置,采用矩形包围,作为初始搜索区域,矩形的边界矩阵为B0=[xminxmaxyminymax]。
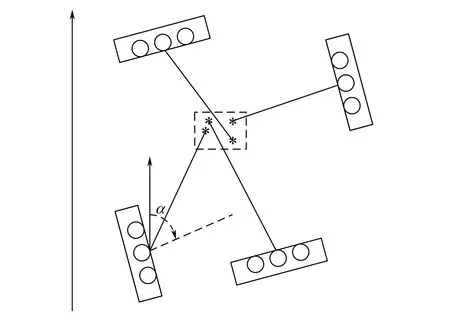
图2 分布式网络定位模型Fig.2 Distributed network location model
3利用区域收缩对声源定位
在混响环境下,采用可控响应功率-相位变换方法对声源进行定位。可控响应功率E(r)为r方向在理论时延下广义互相关-相位变换(GCC-PHAT)函数值的累积,其是视场空间向量r的实值函数,E(r)最大值对应的点为声源的估计位置。考虑M个传感器阵列的2个传感器节点,它们接收到的信号分别为si(n)和sj(n),假设信号从视场中点r*到达2个传感器节点的时间分别为τ(r*,i)和τ(r*,j),则信号到达2个传感器的时延τ=τ(r*,i)-τ(r*,j),传感器节点i、j的SRP值为:
(7)
其中:S(k)为信号s(n)的谱函数;S*(k)为S(k)的共轭函数;L为每帧数据的长度。则阵列中所有的传感器节点在点r*的SRP值为:
(8)
区域收缩法的基本思想为:在特定区域中随机撒下一些点,求解其E(r),然后根据E(r)进行筛选,重新确定搜索区域,通过迭代使搜索区域不断减小,直到确定声源位置。
在使用区域收缩法对声源进行定位时,搜索区域经常发生改变。令Ji(s)为第i次迭代需要重新产生随机点个数,Ni(s)为第i次收缩后筛选出的随机点个数。SRP-PHAT方法在20~25m2区域选取Ni(s)=100,Ji(s)=3000,并不适用于搜索区域改变的情况。基于区域收缩的分布式声源定位方法结合文献[13]的测试结果,并考虑定位精度对参数进行修正,
(9)
(10)
其中:s为搜索区域的面积,单位为m2;[·]表示取整数计算。
4仿真实验与分析
4.1收缩定位仿真
采用采样频率为8kHz的采集器采集的声音信号作为声源的原始信号,在视场为6m×4m的二维平面进行仿真实验。假设声源位置坐标为(3,2),采用4个线性子阵列组成分布式网络对声源进行定位,4个线性传感器子阵列的中心节点坐标分别为(1,0)、(5,0)、(5,4)、(2,4)。子阵列定位与区域收缩定位结果如图3所示。从图3可看出,采用单个线性传感器子阵列对声源进行定位时,存在较大的定位误差,但确定初始矩形搜索区域,结合区域收缩法对声源定位,其定位效果较好。
以采集器采集的声音信号作为声源的原始信号,在视场为3m×3m的区域进行仿真试验,假设声源的真实位置为(2.5,2.5)。声源信号二维能量分布及收缩定位过程如图4所示。从图4可看出,SRP值在整个感应区域分布,采用随机区域收缩法逐步迭代,最终得到声源的位置。
4.2定位性能
基于区域收缩的分布式声源定位方法的定位性能采用均方根误差(RMSE)进行评估,均方根误差为:
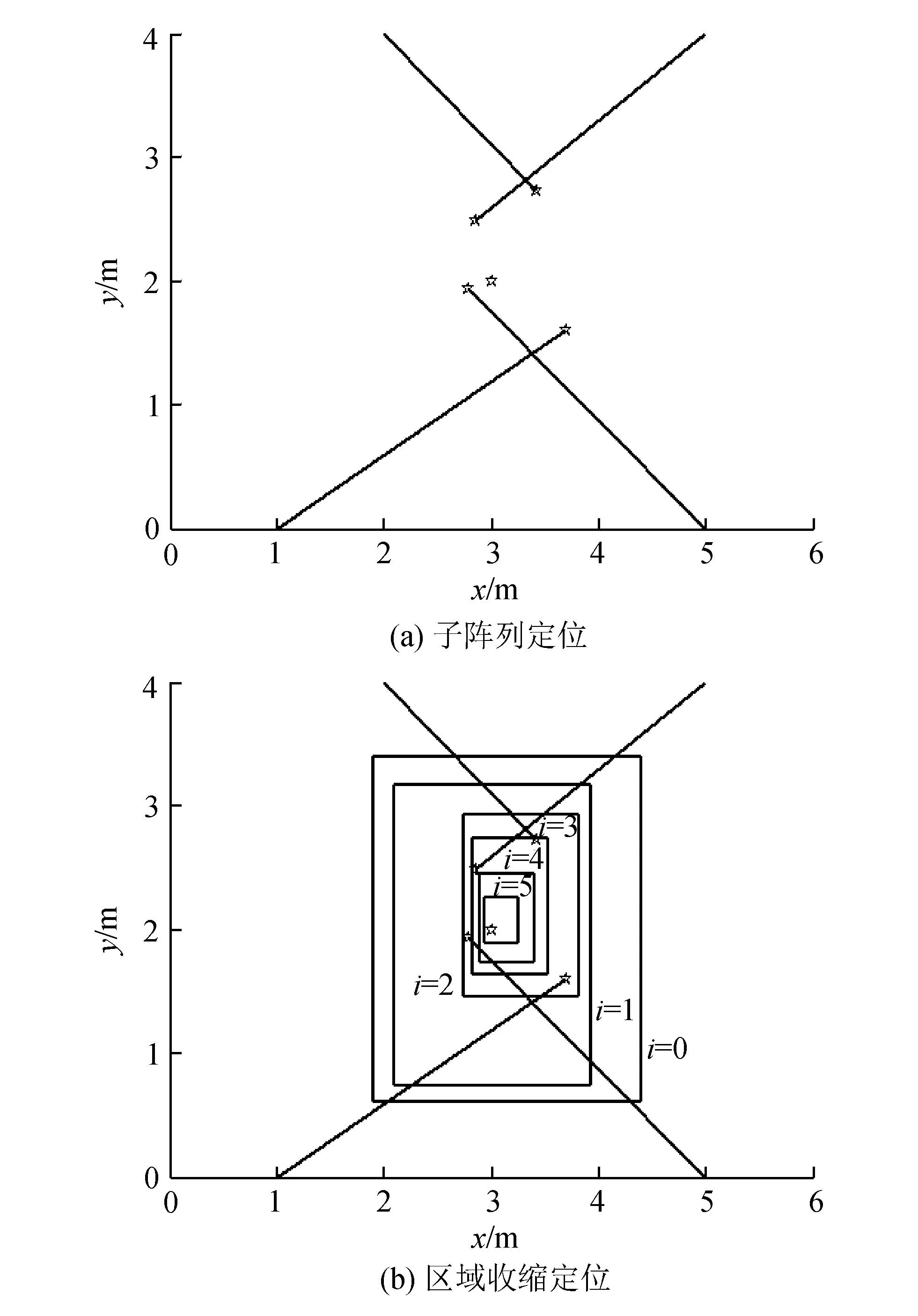
图3 子阵列定位与区域收缩定位Fig.3 Location of sub-arrays and regional contraction
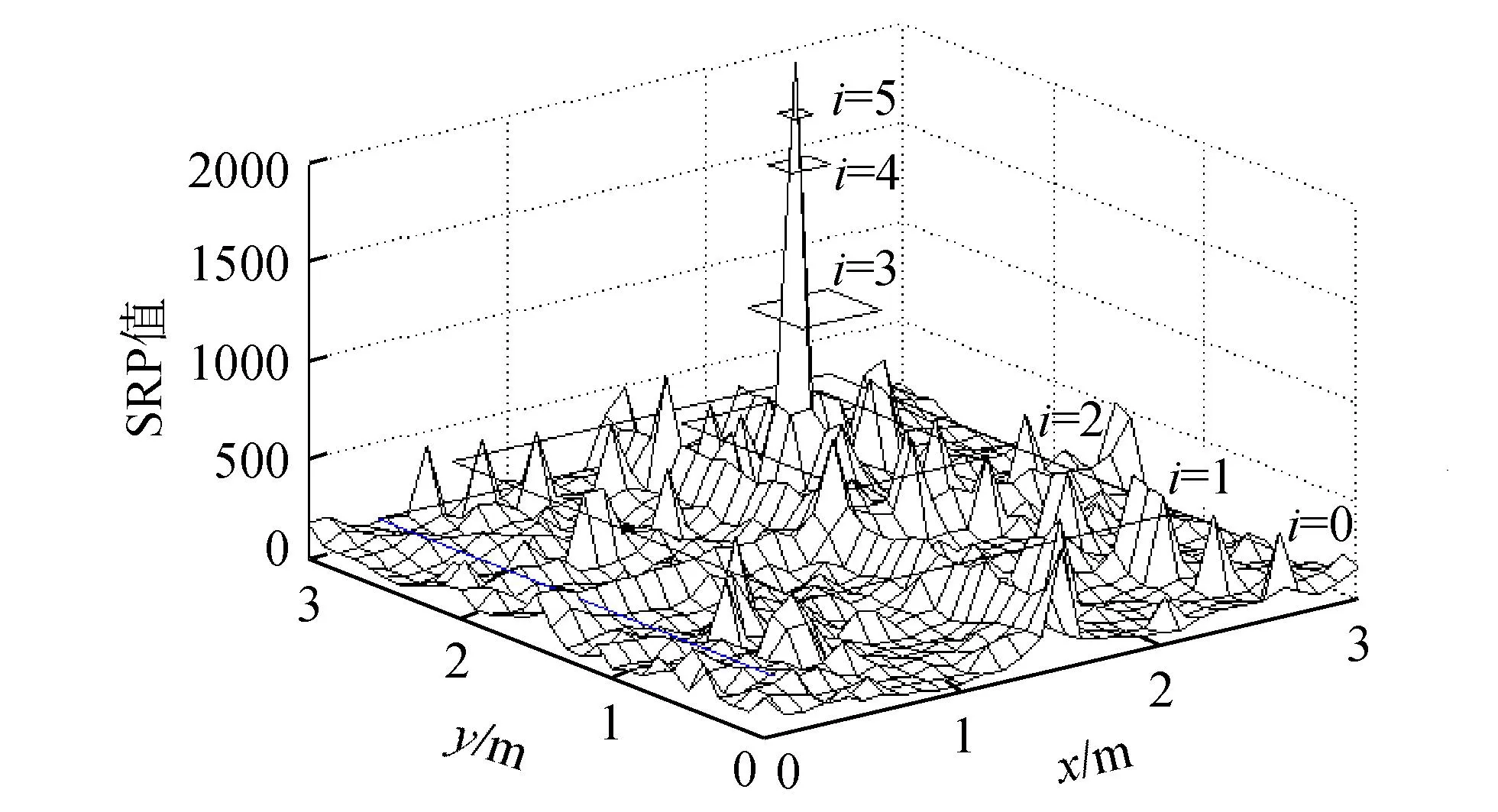
图4 二维能量分布及收缩定位过程Fig.4 Two-dimmensional energy distributionand contraction positioning process
(11)
其中:ρ0为声源的真实位置;ρk为第k次实验的声源位置估计;K=100,即进行100次蒙特卡罗独立实验。在不同迭代次数下,RMSE与信噪比的关系如图5所示。从图5可看出,随着信噪比的增大,定位精度提高,当信噪比大于20dB时,定位误差约为0.5m。基于区域收缩的分布式声源定位方法能够比较准确地估计声源的位置。
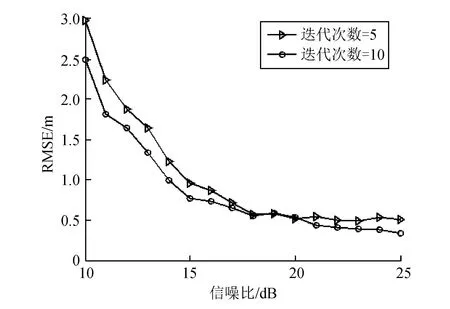
图5 RMSE与信噪比的关系Fig.5 The relationship between RESE and SNR
5结束语
利用线性传感器阵列,提出了一种基于区域收缩的分布式声源定位方法,该方法采用线性子阵列进行初始定位并确定初始矩形搜索区域,然后结合区域收缩法对声源进行定位。仿真实验表明,该方法对声源的定位精度较高。
参考文献:
[1]AVOKHA,ABUTALEBIHR.Speechenhancementusinglinearlyconstrainedadaptiveconstantdirectivitybeam-formers[J].AppliedAcoustics,2010,71(3):262-268.
[2]MARKOVICI,PETROVICI.SpeakerlocalizationandtrackingwithamicrophonearrayonamobilerobotusingvonMisesdistributionandparticlefiltering[J].RoboticsandAutonomousSystems,2010,58(11):1185-1196.
[3]李伟红,汤海兵,龚卫国.公共场所异常声源定位中时延估计方法研究[J].仪器仪表学报,2012,33(4):750-756.
[4]KESHAVARZA,AARABIP.Soundlocalization-basednavigationaluserinterfaces[C]//Proceedingofthe8thIEEEInternationalSymposiumonMultimedia,2006:728-733.
[5]FALLONMF,GODSILLSJ.Acousticsourcelocalizationandtrackingofatime-varyingnumberofspeakers[J].IEEETransactionsonAudio,Speech,andLanguageProcessing,2012,20(4):1409-1415.
[6]ZHANGCha,FLORENCIOLD.Maximumlikelihoodsoundsourcelocalizationandbeamformingfordirectionalmicrophonearraysindistributedmeetings[J].IEEETransactionsonMultimedia,2008,10(3):538-548.
[7]COBOSM,MARTIA,LOPEZJJ.AmodifiedSRP-PHATfunctionalforrobustreal-timesoundsourcelocalizationwithscalablespatialsampling[J].IEEESignalProcessingLetters,2011,18(1):71-74.
[8]MUNGAMURUB,AARABIP.Enhancedsoundlocalization[J].IEEETransactionsonSystems,Man,andCyberneticsPartB:Cybernetics,2004,34(3):1526-1540.
[9]SVAIZERP,BRUTTIA,OMOLOGOM.Useofreflectedwavefrontsforacousticsourcelocalizationwithalinearray[C]//JointWorkshoponHands-freeSpeechCommunicationandMicrophoneArrays,2011:165-169.
[10]CHOUDHARYH,BAHLR,KUMARA.PassiveacousticlocalizationusingblindGauss-Markovestimatewithspectralestimationateachsensor[J].IETRadar,Sonar&Navigation,2013,7(7):800-807.
[11]CANCLINIA,ANTONACCIF,SARTIA,etal.Acousticsorcelocalizationwithdistributedasynchronousmicrophonenetworks[J].IEEETransactionsonAudio,SpeechandLanguageProcessing,2013,21(2):439-443.
[12]ASTAPOVS,PREDENJS,BERDNIKOVAJ.Simplifiedacousticlocalizationbylineararraysforwirelesssensornetworks[C]//18thIEEEInternationalConferenceonDigitalSignalProcessing,2013:1-6.
[13]DOH,SILVERMANHF,YUYing.Areal-timeSRP-PHATsourcelocationimplementationusingstochasticregioncontractiononalarge-aperturemicrophonearray[C]//IEEEInternationalConferenceonAcoustics,SpeechandSignalProcessing,2007:121-124.
编辑:曹寿平
A distributed acoustic localization method based on regional contraction
ZHOU Li, LIU Qinghua
(School of Information and Communication Engineering, Guilin University of Electronic Technology, Guilin 541004, China)
Abstract:In order to improve localization accuracy and reduce the computational complexity of distributed acoustic source localization method, a distributed acoustic source localization based on region contraction is proposed. Multiple linear sub-arrays are used to combine distributed localization arrays, the possible positions of the acoustic sources are preliminary estimated by time delay localization method in linear sub-arrays. Then the initial searching region is determined based on the possible positions. Finally combining with the great controlled response power value, the position of the acoustic source is obtained by the region contraction. The simulation results show that the localization accuracy of the proposed method is high, and the computational complexity is low.
Key words:distributed acoustic source localization; region contraction; searching region
中图分类号:TN911.7
文献标志码:A
文章编号:1673-808X(2016)01-0001-04
通信作者:刘庆华(1974-),女,四川南江人,副教授,博士,研究方向为阵列信号处理与噪声控制。E-mail:qhliu@guet.edu.cn
基金项目:国家自然科学基金(61461012);广西无线宽带通信与信号处理重点实验室主任基金(GXKL0614106);桂林电子科技大学研究生教育创新计划(GDYCSZ201455)
收稿日期:2015-07-08

