一种基于交错格分块的迭代重建算法*
王雪娇, 邱 钧, 刘 畅
(北京信息科技大学 应用数学研究所, 北京 100101)
一种基于交错格分块的迭代重建算法*
王雪娇, 邱钧, 刘畅
(北京信息科技大学 应用数学研究所, 北京 100101)
摘要:交错格采样是二维平行束扫描模式下的一种非传统采样形式, 该采样形式下的投影数据带宽与传统采样的投影数据带宽相近. 引入交错格采样的思想, 对二维平行束扫描模式下传统采样的投影数据进行归组分块, 块内数据具有交错格采样数据的特点, 也具有交错格采样数据的频谱特征, 保留了所有投影数据完整的频谱信息, 一定程度上改善了迭代过程中的误差分配. 由此对块迭代算法进行改进, 形成交错格块迭代算法. 实验结果表明, 在相同迭代次数下, 较之ART图像重建算法, 交错格块迭代算法能有效抑制误差, 提高成像精度.
关键词:图像重建; 投影数据频谱分析; 交错格采样方法; 交错格分块; 块迭代
0引言
在代数迭代图像重建算法中, 块迭代是重要的方法之一, 块迭代格式依赖于对投影数据的归组分块[1-4]. 本文引入A. Faridani给出的交错格采样形式下的理论方法[5-7], 用于对投影数据的归组分块. 该分块方法使得块内的投影数据在频谱上具有优良的特征, 从频谱分析的角度为块迭代校正方法提供一个新的思路[8-10].
在A. Faridani给出的关于平行束采样的理论中, 传统的采样被称为标准格采样, 一种依赖于角度步进调整平行采样步进的采样被称为交错格采样, 本文后续论述中称具有这两种采样形式的投影数据分别为标准格数据和交错格数据. 本文对传统二维平行束采样的投影数据的分块中引入交错格采样的思想, 使得标准的二维平行束采样数据的分块具有交错格数据的特点, 具有交错格数据较为优良的频谱特征. 数据块保留了投影数据所有的频点信息, 利于调整迭代过程中对误差的分配, 并保证成像精度. 基于交错格数据分块的迭代算法, 在对投影数据的分块方法中考虑数据块的频谱特征, 有助于提高成像精度.
1投影数据的标准格采样和交错格采样
标准格采样和交错格采样是二维平行束扫描模式下两种采集方式, 标准格和交错格的定义如下:
定义 1L为一个采样格,
当N=0时, 采样格L为标准格, 记为
当N=P/2时, 采样格L为交错格, 记为
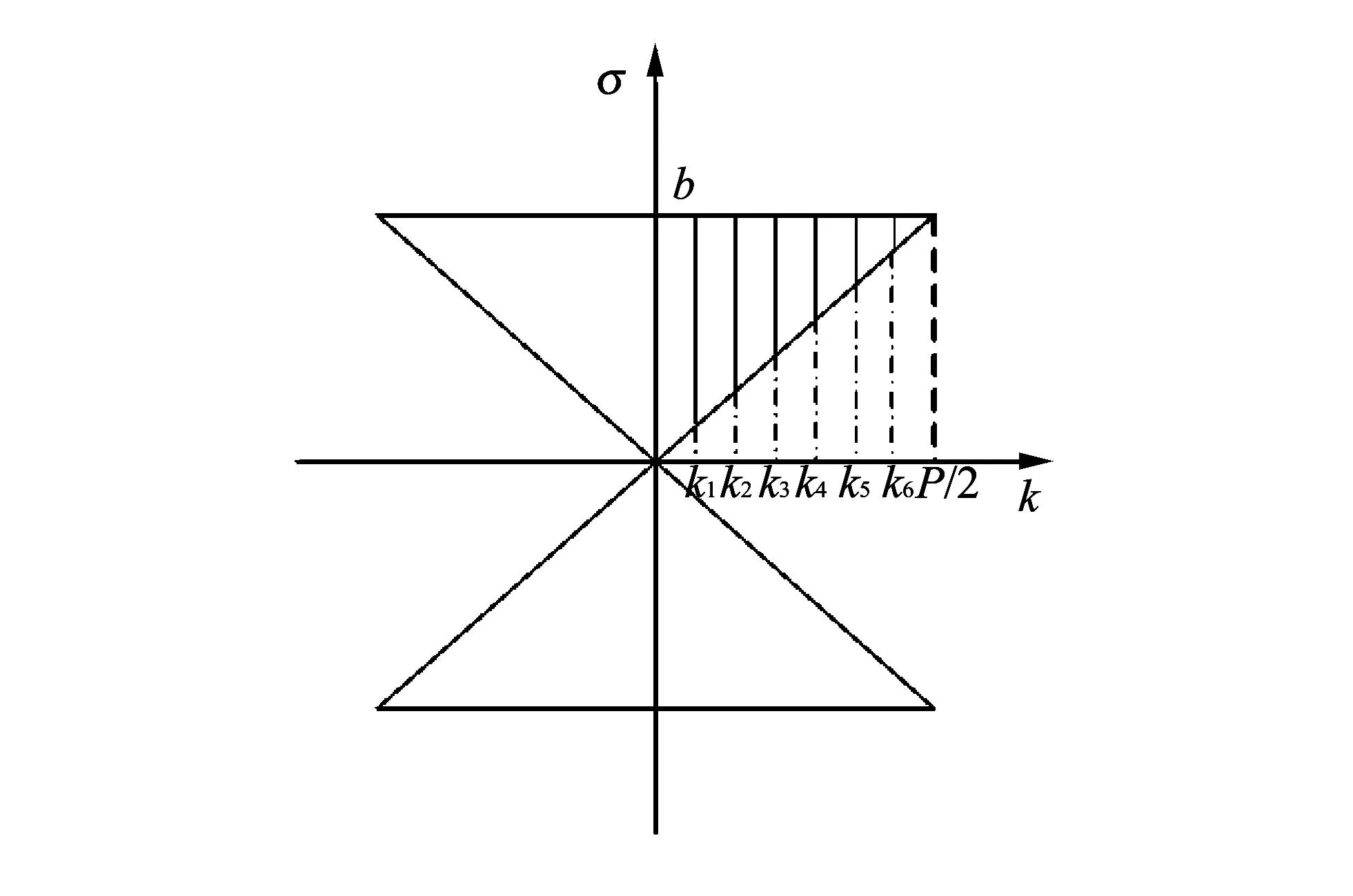
式中:d为扫描射线间隔;m为射线标号;p为采样方向标号;N决定采样方式.d>0,m=0,1,2,…,p=0,…,P-1,N,P均为正数, 且0≤N 当交错格扫描射线间隔为d, 标准格扫描射线间隔为2d, 且二者采样方向数相同时, 标准格数据可以分成两个交错格数据. 2投影数据的频谱分析 本节引入连续投影数据的频谱分析, 分析标准格数据和交错格数据的频谱特点. 2.1连续投影数据的频谱 对连续投影进行二维傅里叶变换, 如式(1)所示 (1) 式中:φ∈T;xr∈R;k∈Z;σ∈R. Frank Natterer[11]结合前人工作, 定义连续投影的频谱集中区域为bow-tie, 安全参数(safety parameter)v∈(0,1), 为简化图形格式以及获得更理想的情况, 设v=0.99, 此时bow-tie的形状如图 1 所示. 图 1 bow-tie示意图(v=0.99)Fig.1 Bow-tie diagrammatic sketch (v=0.99) 2.2离散投影数据的频谱 采样格L定义了对连续投影数据的采样方式, 代表离散投影数据的空域特性, 集合L中的元素代表离散投影数据在φ和xr组成的二维坐标下的位置. 由于实际采集到的投影数据为离散的, 其频谱为连续投影数据频谱的周期性延拓. 连续投影数据频谱的形状为bow-tie, 为明确不同采样格下的投影数据频谱如何进行二维周期性延拓, 给出倒晶格的定义如下 定义 2L⊥(d,N,P为采样格L(d,N,P)的倒晶格, 假设标准格数据射线间隔为d1, 射线的采样方向数为P, 角度采样间隔为2π/P. 当N=0时, 标准格的倒晶格为 即当h1取1,h2取所有整数时, bow-tie的排列在k=P的位置沿纵向展开, 同理, 当h1取其他整数n,h2取遍所有整数时, bow-tie的排列即在k=nP的位置沿纵向展开. 当h1取遍所有整数,h2同时分别取遍所有整数时, 标准格数据频谱如图 2 所示. 图 2 标准格数据频谱(v=0.99)Fig.2 Spectrum of standard lattice data (v=0.99) 假设交错格数据的射线间隔为d2=2d1, 射线的采样方向数为P. 交错格采样过程中, 每旋转一个角度, 射线位置平行移动d1. 当N=P/2时, 交错格的倒晶格为 即当h1取0,h2取所有整数时, bow-tie的排列如图 3 所示, 同理, 图 4 为当h1取n,h2取所有整数时, bow-tie的排列示意图. 图 3 h1取0, h2取所有整数时的bow-tie排列示意图Fig.3 Bow-tie diagrammatic sketch forh1 taking 0, h2 taking all integers 由上述分析, 交错格数据的频谱如图 5 所示. 交错格数据的频谱带宽b′与标准格数据频谱带宽b相近, 保证了投影数据所有频谱信息的完整性, 由交错格数据进行图像重建, 理论上能够获得与标准格数据进行重建相近的分辨率. 同时, 投影数据分成的具有交错格数据特点的块可以在迭代过程中用于误差校正, 有效地利用这一思路, 建立优化的校正过程, 可以提高成像精度. 图 4 h1取n, h2取所有整数时的bow-tie排列示意图 Fig.4 The bow-tie diagrammatic sketch forh1 taking n, h2 taking all integers 图 5 交错数据频谱(v=0.99)Fig.5 Spectrum of interlaced latice data (v=0.99) 3基于交错格数据的块迭代算法 本节将标准的二维平行束扫描的投影数据分成两个不同的交错格数据块, 进行块迭代重建[12-13], 该方法能够提高成像精度. 3.1基于交错格数据的分块方法 3.2基于交错格数据的块迭代算法 基于交错格数据对投影数据进行分块的交错格块迭代步骤如下: 2) 由数据块G1中第1根射线开始进行第1次迭代, 将X(0)代入式(2)中进行迭代, 得结果X(1); 以X(1)作为初始值, 对数据块G2中的第2根射线进行第2次迭代; 3) 第i次迭代时, 若i≤P·M/2, 则选择数据块G1中的第i根射线进行迭代, 若i>P·M/2, 则选择数据块G2中的第(i-P·M/2)根射线进行迭代; 4) 第(P·M)次后停止一轮迭代. 迭代过程中块内数据采用逐线迭代, 权重依次分配, 一次迭代结束, 一个数据块的迭代结果作为另一个数据块的初始值进入下一次迭代, 依次循环此过程. 两个数据块每一次的迭代结果相互参照、 校正, 有助于减少误差累积, 提高成像精度. 由此, 本文设计了经过修正的基于逐线校正方式的迭代格式[14]如下 (2) 式中:αn为松弛因子;ai为第i条射线的加权系数;yi为第i条射线的投影值. 基于交错格数据的特点对投影数据分块, 分成的两个数据块的频谱信息完整, 由其中一个块重建图像能够保证成像精度. 由此对投影数据进行块迭代算法的调整, 很好地改善了迭代中的误差分配, 一定程度上提高了重建结果的成像精度. 4数据实验 4.1模拟数据的数值实验 本节选择ART算法和交错格块迭代算法对两组模拟数据进行实验验证. 两组模拟数据的角度采样数为576, 平行线采样数为721, 重建图像采用的分辨率为600×600. 以下给出两组测试图像的原图, 分别采用ART算法和交错格块迭代算法迭代1轮, 3轮, 5轮, 显示重建图像, 并给出结果和原图第300行的像素曲线, 如图6~图10所示. 误差分析表 1, 表 2 采用归一化均方距离判断d和归一化平均绝对值距离判断r来评价ART算法与交错格块迭代算法的重建图像质量. 图 6 两组原图及第300行所在位置Fig.6 Two original images and the position of the 300th row 迭代方法迭代次数归一化均方距离判断d归一化平均绝对距离判断r迭代时间/sART10.40480.529417.74130.33550.370930.38150.30040.287648.242交错格块迭代10.39990.395510.08530.24470.228629.53450.21190.183648.878 图 7 Sheep-logan图ART迭代不同轮次的重建结果Fig.7 Reconstruction results of ART under different numbers of iterations for sheep-logan image 图 8 Sheep-logan图交错格块迭代不同轮次的重建结果Fig.8 Reconstruction results of interlaced lattice block under different numbers of iterations for sheep-logan image 图 9 鹦鹉图ART迭代不同轮次的重建结果Fig.9 Reconstruction results of ART under different numbers of iterations for parrot image 图 10 鹦鹉图交错格块迭代不同轮次的重建结果Fig.10 Reconstruction results of interlaced lattice block under different numbers of iterations for parrot image 实验结果表明, 相同迭代次数下, 交错格块迭代算法重建后的图像误差相对更小, 重建后图像的质量也更好. 随着迭代次数的增加, 交错格块迭代算法重建的图像与原图像的差距不断减小, 对边缘的重建效果也明显好于ART算法, 由此表明交错格块迭代算法可以在一定程度上提高成像的精度. 表 2 鹦鹉图ART和交错格块迭代一定次数后的误差分析表 4.2实测数据的数值实验 本节采用标准二维平行束采样下的实测陶瓷叶片的数据重建图像, 采用ART和交错格块迭代算法迭代不同轮次, 比较重建图像的裂纹变化情况. 实测数据量为576×281, 重建采用的分辨率为256×256, 实测数据位图如图 11 所示. 重建结果如图 12 和图 13 所示. 图 12 和图 13 的像素曲线可以看出, 随迭代次数增加, 图像灰阶变化愈加明显, 细节愈加突出, 较ART算法, 交错格块迭代算法更能突出陶瓷细小裂纹特征, 一定程度上提高了成像精度. 图 11 实测投影数据位图Fig.11 Measured projection data bitmap 图 12 陶瓷叶片图ART迭代不同轮次的重建结果Fig.12 Reconstruction results of ART under different numbers of iterations for ceramic blade image 图 13 陶瓷叶片图交错格块迭代不同轮次的重建结果Fig.13 Reconstruction results of interlaced lattice block under different numbers of iterations for ceramic blade image 5结论 本文对标准二维平行束采样下的投影数据的分块中, 引入交错格采样方法的思路, 保持了必须依赖于角度步进的平行采样的可变步进调整, 得以通过将标准二维平行束采样下的投影数据按交错格采样的思想进行归组分块, 并保证块内数据频谱信息的完整性, 改善了迭代过程中的误差分配, 形成基于交错格数据分块的迭代算法. 数据实验表明该方法能有效提高重建图像的精度, 减小误差. 如何针对投影数据设计基于交错格数据频谱分析的更为合理有效的分块, 以进一步提高成像精度, 以及如何在保持现有成像精度的基础上, 用更少的数据进行迭代成像等等[15], 值得进一步研究, 这一研究有助于形成应用于实际的快速迭代算法. 参考文献: [1]张朋, 张兆田. 几种 CT 图像重建算法的研究和比较[J]. CT 理论与应用研究, 2001, 10(4): 4-9. Zhang Peng, Zhang Zhaotian. Research and comparison several CT reconstruction algorithmsv[J]. CT Theory and Applications , 2001, 10(4): 4-9.(in Chinese) [2]Jiang Ming, Wang Ge. Development of iterative algorithms for image reconstruction [J]. Journal of X-ray Science and Technology (Invited Review), 2002, 10: 77-86. [3]邱钧, 徐茂林. 由投影重建图像的对称块迭代算法[J]. 电子与信息学报, 2007, 29(10): 2293-2300. Qiu Jun, Xu Maolin. A method of symmetric block-iterative for image reconstruction[J]. Journal of Electronics & Information Technology, 2007, 29(10): 2293-2300.(in Chinese) [4]陈建林, 闫镔, 李磊, 等. CT 重建中投影矩阵模型研究综述[J]. CT 理论与应用研究, 2014, 23(2): 317-328. Chen Jianlin, Yan Bin, Li Lei, et al. Reviews of the model of projection matrix of CT reconstruction algorithm [J]. CT Theory and Applications, 2014, 23(2): 317-328. (in Chinese) [5]Faridani A. Inverse problems, tomography, and image processing: sampling in parallel-beam tomography[M]. US: Springer, 1998. [6]Faridani A. Reconstructing from efficiently sampled data in parallel-beam computed tomography[J]. Inverse problems and imaging, Pitman Research Notes in Mathematics Series, 1991, 245: 68-102. [7]Faridani A. Sampling, wavelets, and tomography: sampling theory and parallel-beam tomography[M]. Boston: Springer, 2004. [8]王小璞, 张朋, 李兴东. 一种块迭代的快速代数重建算法[J]. CT 理论与应用研究, 2000, 9(z1): 10-12. Wang Xiaopu, Zhang Peng, Li Xingdong. A fast ART algorithm based on block iteration[J]. CT Theory and Applications, 2000, 9(z1): 10-12.(in Chinese) [9]高雪妮, 玉振明, 张军, 等. 基于多级分块迭代法的不同聚焦图像融合[J]. 电子学报, 2011, 39(3): 690-694. Gao Xueni, Yu Zhenming, Zhang Jun, et al. Multi-focus image fusion based on multi-level and iterative method[J]. Acta Electronica Sinica, 2011, 39(3): 690-694. (in Chinese) [10]邱钧, 王亮. 由投影重建图像的对称网格迭代算法[J]. CT 理论与应用研究, 2007, 16(2): 20-30. Qiu Jun, Wang Liang. Symmetric mesh-iterative algorithms for image reconstruction[J]. CT Theory and Applications, 2007, 16(2): 20-30. (in Chinese) [11]Natterer F. The mathematics of computerized tomography [M]. New York: Wiley, 1986. [12]Jiang Ming, Wang Ge. Convergence studies on iterative algorithms for image reconstruction [J]. IEEE Transactions on Medical Imaging, 2003, 22(5): 569-579. [13]Qu Gangrong, Wang Caifang, Jiang Ming. Necessary and sufficient convergence conditions for algebraic image reconstruction algorithms[J]. IEEE Trans. image processing, 2009, 18(2): 435-440. [14]庄天戈. CT原理与算法[M]. 上海: 上海交通大学出版社, 1992. [15]邹晶, 孙艳勤, 张朋. 由少量投影数据快速重建图像的迭代算法[J]. 光学学报, 2009, 29(5): 1198-1204. Zou Jing, Sun Yanqin, Zhang Peng. A fast iterative image reconstruction algorithm from few-views projections data [J]. Acta Optica Sinica (SSIN), 2009, 29(5): 1198-1204. (in Chinese) A Block Iterative Reconstruction Algorithm Based on Interlaced Lattice WANG Xue-jiao, QIU Jun, LIU Chang (Institute of Applied Mathematics, Beijing Information Science & Technology University, Beijing 100101, China) Abstract:Interlaced lattice sampling is a kind of non-traditional sampling form of two-dimensional parallel beam scanning mode. The projection data bandwidth of interlaced lattice sampling is close as the traditional sampling. The idea of interlaced lattice sampling was introduced to block the traditional sampling projection data of two-dimensional parallel beam. The data of this block has the characteristics of interlaced lattice sampling data, and also has frequency spectrum characteristics of interlaced lattice sampling data. The data of this block reserves complete frequency spectrum information of all projection data, and it improves the distribution of the error during the iteration to some extent. Thus an interlaced lattice block iterative algorithm has formed to improve block iterative algorithm. The experimental results show that, under the same number of iterations, compared with ART image reconstruction algorithm, interlaced lattice block iterative algorithm can effectively restrain the error and improve the imaging accuracy. Key words:image reconstruction; spectrum analysis of projection data; interlaced lattice sampling method; interlaced lattice block; block iterative 中图分类号:TP391 文献标识码:A doi:10.3969/j.issn.1673-3193.2016.01.014 作者简介:王雪娇(1988-), 女, 硕士生, 主要从事图像重建的研究. 基金项目:国家自然科学基金项目 (61372150, 61271425) *收稿日期:2014-12-22 文章编号:1673-3193(2016)01-0067-09