基于边缘检测的位图矢量化的实现*

吴兴蛟　吴　晟

(昆明理工大学信息工程与自动化学院　昆明　650500)



基于边缘检测的位图矢量化的实现*

吴兴蛟吴晟

(昆明理工大学信息工程与自动化学院昆明650500)

摘要论文介绍的是基于边缘检测与特征点提取的位图矢量化方法。先将位图进行RGB—HSI变换,增强图像对比度并进行边缘降噪、平滑处理,而后对图片进行阈值化处理。运用Canny算子对阈值化图像进行边缘检测,并藉此提取边缘轮廓。获得边缘轮廓后对其进行特征点求取。得到特征点集合。存储集合并在此基础上借助Matlab编写曲线处理函数,使用最小二乘法对曲线进行局部试拟合,比对SSE,找出最小值并记住当前参数,确定拟合函数。通过对所有局部曲线自动拟合技术,生成一组多项式方程,实现位图的矢将其量化。最后得出一组图像曲线。论文借助边缘检测的技术实现了位图的矢量化。

关键词边缘检测; 曲线自动拟合; 矢量化; 特征点提取; Matlab; 多项式拟合; 最小二乘法

Bitmap Vector Quantization Based on Edge Detection

WU XingjiaoWU Sheng

(School of Information Engineering and Automation, Kunming University of Science and Technology, Kunming650500)

AbstractA bitmap vectorization methods that based on edge detection and feature point extraction is introduced in this article. Firstly, RGB-HSI transform is used to enhance the image contrast of the bitmap, to reduce the edge’s noise and smooth the edge, then applying the threshold to process the image. Using Canny operator to detect the edge of the threshold image, and to extract the edge contour. Striking the characteristic points of the edge contour, thus getting feature points set. Combining Matlab to write the curve processing function on the basis of the set storage, using the least square method to fit the curve and to compare the SSE. Then finding the minimum value and remembering the current parameters, and determining the fitting function. Through automatic fitting technique to assemble all local curves, thus generating a set of polynomial equations, then realizing the vector of bitmap and quantizing them. Finally, a set of image curves are obtained. In this paper, edge detection technology is used to achieve the vectorization of a bitmap.

Key Wordsedge detection, automatic fitting curve, vectorization, extracte of feature point, Matlab, polynomial fitting, the least square method

Class NumberTP391.41

1引言

图形(图像)通常以不同形式存储在计算机中,并用不同的方式加以描述。位图和矢量图是其中最常用的两种描述方式。位图采用像素点来描述图像。每个点用二进制数据来描述其颜色与亮度等信息,这些点是类似于点阵的离散点,多个像素的色彩组合形成位图。矢量图则是用一系列计算机指令来描述和记录图,图可以分解为一系列由点、线、面等组成的子图,矢量图所记录的是对象的几何形状、线条粗细和色彩等。图像形式可随坐标迁移[1]。

一般来说,对色彩要求较为严格、表现力要求较强、图层力求细腻、图像层次多、细节多的图多采用位图来描述。矢量图则多用在工程制图、标志、字体等这些构图较为简单且由规律的线条组成的图形描述。矢量图可以任意缩放,且其图形整体形状变化不大。而位图放大到一定程度后,就会产生模糊,甚至边缘出现锯齿。

矢量图从本质上是使用曲线方程对图形进行的精确描述,在以像素为基本显示单元的显示器或打印机上是无法直接表现的。只有通过栅格化将矢量图转换成以像素点阵来表示的信息,再加以显示或打印。在目前技术之下,对图像的栅格化已是较为完善的。但随着显示器分辨率的差距越来越大。以及大数据时代的到来。我们面临数据存储、显示的难题越来越大。一幅图,有无较好的可移植性是评判其优劣的标准之一。以保证图像在放大缩小的时候失真率较小。便有了位图的矢量化。将位图矢量化,该过程是一个离散数据连续化的过程。其间涉及对离散数据的拟合。位图矢量化的过程就是逆栅格化。

逆栅格化就是通过一系列采样、抽象,得到可以描绘一个图形的点线集合。然后通过合理的模型提取抽象出表达函数。

采样、抽象的过程具体来说就是数理统计的过程,一个对象是否能被统计是取决于样本处理的结果的,所以在取样之前,应该对样本进行处理。使其满足取样的最低需求。在此处,取的样本是要可以描绘图像边缘特征的部分,所以在取样之前,应该对其对比度进行处理。以便抽取对象轮廓。要进行曲线的拟合,就是要对边缘曲线进行特征点获取。然后对这些点进行曲线拟合。所以对于该问题可采用提取轮廓点、轮廓点矢量化的方法来完成位图矢量化。大致分四步完成:

1) 图像预处理;

2) 边缘检测;

3) 特征点提取;

4) 曲线拟合。

2图像预处理

对图像的预处理是为了平滑图像边缘、消除毛刺、消除干扰、提高图像的对比度,让其在边缘检测时能更加有效地提取出连续的边缘轮廓[2~3]。

2.1采用HSI空间处理原始RGB图像。

RGB和HSI模型是两种最常用的颜色模型。RGB模型基于三基色原理,面向硬件,便于颜色的采集和显示。HSI模型基于色调、饱和度和强度三种基本特征量来感知颜色,反映了人的视觉系统感知彩色的方式。而且HSI模型就是为了满足计算机数字化颜色管理的需要而提出的对上述颜色模型的高度抽象模拟的数学模型。且在基于颜色空间划分,RGB关联太大,每个通道都编入了亮度信息,容易受周围环境的影响而HSI空间就不会。HSI空间是从人的视觉系统出发,有较好抗干扰能力,有利于优化模型。所以适合选用HIS空间处理[4~5]。

位图RGB—HSI变换采用如下程序实现:

rgb=imread('图片名(图片路径)');

Info=imfinfo('./test.bmp')

rgb=im2double(rgb); %转换成双精度

r=rgb(:,:,1); %RGB图像中R分量

g=rgb(:,:,2); %RGB图像中G分量

b=rgb(:,:,3); %RGB图像中B分量

num=0.5*((r-g)+(r-b));

den=sqrt((r-g).^2+(r-b).*(g-b));

theta=acos(num./(den+eps));

H=theta;

H(b>g)=2*pi-H(b>g);

H=H/(2*pi);

num=min(min(r,g),b);

den=r+g+b;

S=1-3.*num./(den+eps);

H(S==0)=0;

I=(r+g+b)/3;

S=im2uint8(S);

H=im2uint8(H);

I=im2uint8(I);

2.2增大图像对比度

为了得到更易于提取边缘的图像,采用一些技术去改善图像的视觉效果,将图像转换成一种更适合于人或机器进行分析处理的形式。有选择地突出某些对人或机器分析有意义的信息,抑制无用信息,提高图像的使用价值。故而在此增加图像的对比度。采用式(1)实现:

imadjust(I,[low_in;high_in],[low_out;high_out])

(1)

2.3阈值化图像

图像阈值化,就是将灰度图像或者RGB彩色图像上的像素点的灰度值通过阈值规范化为0或1,也就是使整个图像呈现出明显的黑白对比效果。图像阈值化有利于统计的进一步处理,使数据量得到精简。对于简单图像的处理,采用全局阈值处理即可。采用式(2)实现:

BW=im2bw(I,level)

(2)

及此完成对于图像的初步处理。得到所需要的阈值化图像。

3边缘检测

对图像边缘轮廓的提取有许多的研究和方法[6],常用的图像的边缘提取的梯度算子分为一阶和二阶算子。

一阶:Roberts Cross算子,Prewitt算子,Sobel算子,Kirsch算子,罗盘算子;

二阶:Marr-Hildreth,zerocmss算子,Canny算子,Laplacian算子。

在此做出简要说明。

1) Soble:离散性差分算子,常运用计算图像亮度函数的梯度之近似值。使用此算子,将会产生对应的梯度矢量或其法矢量。

2) Prewitt:一阶微分算子,利用像素点四连通域的灰度差,利用极值检测边缘,去掉部分伪边缘,具有平滑噪声的作用。利用水平与垂直两个方向模板与图像进行邻域卷积完成边缘检测。

3) Roberts:利用局部差分算子寻找边缘的算子,边缘定位的精度较低。

4) Log:将高斯滤波和拉普拉斯检测算子结合在一起进行边缘检测的方法,图像先与高斯滤波器进行卷积,再进行拉普拉斯卷积变换,最后再进行过零判断。

5) Canny:首先使用高斯平滑函数平滑与消除噪声;运用一阶差分卷积模板进行边缘增强;进行非极大值抑制(NMS)。保留梯度方向上的最大值。

在对多种算子进行检验分析之后。得出如下结论:

1) Sobel算子适用于灰度渐变的图像处理,但缺点是对变化不大的部位处理效果不好以及边缘定位不准确;

2) Prewitt算子对灰度渐变的图像处理效果较好,但是提取的图像边缘的间断点较多;Log算子比前面几种方法要好,但是边缘的间断点也较多;

3) Roberts算子对具有陡峭的低噪声的图像处理效果较好,但是提取的边缘比较粗,因此对边缘的定位不是很准确;

4) Log方法先对原始图像进行平滑处理,极大程度地抑制了噪声干扰,但是处理之后仍发现存在对噪声敏感,噪声平滑能力与边缘定位能力相矛盾等缺点

5) Canny方法不容易受噪声干扰,能够检测到真正的弱边缘,原因是它使用两种不同的阈值分别检测强边缘和弱边缘,并且当弱边缘和强边缘相连时,可以将弱边缘包含在输出图像中。

故而本文最终采用Canny算子实现边缘提取[7]。

对图像进行预处理以后,利用Canny算子对其进行边缘检测,检测过程如下:

1) 用高斯滤波模板对原图像进行卷积以消除噪声;

2) 利用导数算子找到图像灰度沿着两个(x,y)方向的偏导数,并求出梯度的大小;

3) 利用2)的结果计算出梯度的方向;

4) 把边缘的梯度方向大致分四种:0°、45°、90°、135°方向。通过梯度的方向,找到这个像素梯度方向的邻接像素;

5) 遍历图像,若某个像素的灰度值与其梯度方向上前后两个像素的灰度值相比不是最大的,那么这个像素值为零,即不是边缘;

6) 使用累计直方图计算两个阈值,大于高阈值的一定是边缘,小于低阈值的一定不是边缘,介于之间的,看这个像素的邻接像素中有没有超过高阈值的边缘像素,如果有的话那么它就是边缘,否则它就不是边缘。

实现见式(3):

BW=edge(I,'canny',thresh)

(3)

根据所指定的敏感度阈值thresh,用Canny算子进行边缘检测,它忽略了所有小于阈值的边缘。当thresh为空时,自动选择阈值。

至此提取出边缘矩阵BW。

4特征点提取

特征点的提取是位图矢量化过程中重要的一步,该步骤主要是从检测出的边缘中提取出表示图像轮廓关键特征的点。轮廓特征点包括角点、切点和拐点,其中角点是目标轮廓线上曲率超过一定阈值的局部极大值点,切点是圆弧和直线的平滑过渡点,拐点是凹圆弧和凸圆弧的平滑过渡点。目前绝大多数的轮廓特征点提取方法都是利用相邻的一组轮廓点来计算轮廓线上各点的曲率或两近似直线段的夹角来判定轮廓特征点的,角点的曲率较大,比较容易提取。此处采用的Harris算法是稳定性和准确度都较高的基于灰度的角点检测算法[8]。

Harris算法提取特征点的具体步骤如下:

1) 使用高斯滤波与图像进行卷积,滤除噪声;

2) 使用37像素圆形模板依次遍历图像,求出各点梯度;

3) 对于每一像素点,计算其对应的二阶方阵;

4) 计算各像素点的响应;

5) 用非最大值抑制求得R(x,y)的局部最大值,则该局部最大值对应的像素点即为角点。

具体见以下程序

f=BW;

ori_im=double(f)/255; %unit8转化为64位双精度double64

fx = [-2 -1 0 1 2]; % x方向梯度算子(用于Harris角点提取算法)

Ix = filter2(fx,ori_im); % x方向滤波 善于使用filter

fy = [-2;-1;0;1;2]; % y方向梯度算子(用于Harris角点提取算法)

Iy = filter2(fy,ori_im); % y方向滤波

Ix2 = Ix.^2;

Iy2 = Iy.^2;

Ixy = Ix.*Iy;

clear Ix;

clear Iy; %消除变量

h= fspecial('gaussian',[10 10],2); % 产生10*10的高斯窗函数,sigma=2 标准偏差

Ix2 = filter2(h,Ix2);

Iy2 = filter2(h,Iy2);

Ixy = filter2(h,Ixy); %分别进行高斯滤波

height = size(ori_im,1);

width = size(ori_im,2);

result = zeros(height,width); % 纪录角点位置,角点处值为1 ,背景都是黑色的

R = zeros(height,width);

Rmax = 0; % 图像中最大的R值以便设置门限

for i = 1:height

for j = 1:width

M = [Ix2(i,j) Ixy(i,j);Ixy(i,j) Iy2(i,j)]; %2*2的矩阵

R(i,j) = det(M)-0.06*(trace(M))^2; % 计算R ,求得RMAX,看来是整体求得的,角点响应函数

if R(i,j) > Rmax

Rmax = R(i,j);

end;

end;

end;

cnt = 0; %记录点数的

for i = 2:height-1

for j = 2:width-1 % 进行非极大抑制,窗口3*3

if R(i,j) > 0.01*Rmax &&

R(i,j) > R(i-1,j-1) &&

R(i,j) > R(i-1,j) &&

R(i,j) > R(i-1,j+1) &&

R(i,j) > R(i,j-1) &&

R(i,j) > R(i,j+1) &&

R(i,j) > R(i+1,j-1) &&

R(i,j) > R(i+1,j) &&

R(i,j) > R(i+1,j+1)

result(i,j) = 1;

cnt = cnt+1;

end;

end;

end;

[posc, posr] = find(result == 1);

cnt; % 角点个数

figure;

imshow(ori_im*255) %和 X的效果是一样的

hold on;

plot(posr,posc,'g+');

5曲线拟合

最后进行的操作是曲线的拟合,在此我们采用的是曲线的自动拟合。设计思想是:在确定特征点数组之后,便对曲线进行动态分组—将相邻的几个点用最小二乘法进行试拟合[9],对比其和方差(SSE),找出最小的SSE和此时的分段数目。以及最佳的拟合系数。由于矢量图的构造一般由曲线或者直线等简单线段构造而成。所以拟用多项式来拟合目标曲线。而通过对不同曲线的SSE比较找出最佳拟合曲线[10]。实现细节是通过两个嵌套循环实现。

5.1SSE(和方差)

该统计参数计算的是拟合数据和原始数据对应点的误差的平方和,计算公式如式(4):

(4)

SSE越接近于0,说明模型选择和拟合越好,数据预测也越成功。

5.2多项式拟合

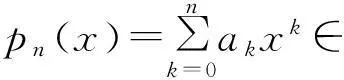
(5)

当拟合函数为多项式时,称为多项式拟合,满足式(1)的称为最小二乘拟合多项式。特别地,当n=1时,称为线性拟合或直线拟合。

显然

(6)

为a0,a1,…,an的多元函数,因此上述问题即为求I=I(a0,a1,…,an)的极值问题。由多元函数求极值的必要条件,得

(7)

即

(8)

5.3多项式拟合的一般方法

1) 由已知数据画出函数粗略的图形——散点图,确定拟合多项式的次数n;

3) 写出正规方程组,求出a0,a1,…,an;

在实际应用中,n

经过实验,发现当采用傅里叶函数和高斯函数对特征点进行曲线拟合时,剩余平方和较大(接近10的5次方左右),拟合曲线与散列点的对应较弱。故将原曲线进行区域化拟合,即将散列点分组拟合。

对于分组的点,可通过程序循环进行控制,截取3~8个不同组成形式的点,进行曲线试拟合,通过对拟合曲线中小于1的剩余平方和的统计,对比得出其剩余平方和在区间0~1的点数组合。

对于拟合阶次的选定同样通过循环,先将原边缘特征点集合分为N组,N是由点总数与点数组合相除。对多项式介词的选择根据点数组合求得。通过对不同系数的剩余平方和的比较,找出其中最小数标记出来,记为该区域曲线的最佳阶次。将最佳阶次代入到方程中,即得到最终的方程,

下面为实现代码见以下程序

for s=3:8

count(s)=oper(posr,posc,cnt,s)

end

fprintf('m是最大值,n是最大值的位置 ');

[m n]=max(count)

fprintf('对比后的拟合函数 ');

count=oper(posr,posc,cnt,n)

function countSSE=oper(xGet,yGet,totoal,pointGet)

%函数实现的功能是通过x和y向量组提供横纵坐标,然后通过坐标点总数,以及取点个数建立函数返回统计后剩余平方和小于1的函数

%countSSE=oper(xGet,yGet,totoal,pointGet)

xw=xGet;

yw=yGet;

cnt=totoal;

point=pointGet;

countSSE=0;

number=floor(cnt/point)%分段数

temp=cnt;

cnt=cnt-mod(temp,number)

for k=temp+1:1:cnt

xw(k)=0;

yw(k)=0;

end

for j=1:1:number

fprintf(1,'计算第%d段函数 ',j);

x=xw(((j-1)*(cnt/number)+1):((j)*(cnt/number)+1));

warning('off')

y=yw(((j-1)*(cnt/number)+1):((j)*(cnt/number)+1));

warning('off')

nx = length(x);

ny = length(y);

n = length(x);

if nx == ny

x1 = x(1); xn = x(n);

% n个数据可以拟合(n-1)阶多项式,高阶多项式多次求导,数值特性变差

%自动赋值m

for m=1:point

[p,S]=polyfit(x,y,m);

warning('off')

[yh,delta]=polyconf(p,x,S);

SSE(m)=sum((y-yh).^2);

end

[sd,m]=min(SSE);

fprintf('输出最适m=%d',m);

[p,S]=polyfit(x,y,m);

fprintf(' 输出多项式');

poly2sym(p)

disp ' 输出多项式的有关信息 S'

disp (S)

[yh,delta]=polyconf(p,x,S);

% 拟合效果和精度检验

SSE=sum((y-yh).^2);

if SSE<1

countSSE=countSSE+1;

end

RMSE = sqrt(SSE / (n - 2));

R_square = sum((yh-mean(y)).^2)/sum((y-mean(y)).^2);

fprintf (1,' 剩余平方和 SSE = %3.6f ',SSE)

fprintf (' ')

fprintf (1,' 标准误差 RMSE = %3.6f ',RMSE)

fprintf (' ')

fprintf (1,' 相关指数 R-square = %3.6f ',R_square)

fprintf (' ')

else

clear

zxecf

end

end

6结语

模型采用多项式拟合作为模型范式,采用SSE(剩余平方和)与零的趋近程度评价当前拟合与数据之间的关系。该模型先采用循环筛选取值间隔,然后在同理采用循环选择阶次,最后构造出函数。该模型自动化程度较高[11]。可运用于大部分图形转化。在对不同图形选取之时,只要改变选取图片路径,其余对于分组以及参数的选取都有程序自动计算得出。普适性较高。同时在对图像进行处理之前,先对其进行优化处理。从而保证了输出结果的准确性。

模型通过提取位图的函数特征。自动构造矢量图函数表达式。可为位图矢量化下一步研究提供一定助力。

参 考 文 献

[1] 卢迪,李大辉,吴海涛.计算机图形学原理及应用[M].北京:国防工业出版社,2009:1-125.

LU Di, LI Dahui, WU Haitao. Principles of computer graphics and applications[M]. Beijing: National Defense Industry Press,2009:1-125.

[2] 严素蓉,朱桂林,徐从富.一种位图矢量化新方法[J].计算机工程与应用,2005,14:85-87.

YAN Surong, ZHU Guilin, XU Congfu. A new method of vector quantization bitmap[J]. Computer Engineering and Application,2005,14:85-87.

[3] Rafael C. Gonzalez, Richard E. Woods, Steven L. Eddins.数字图像处理[M].北京:电子工业出版社,2005,9:224-272.

Rafael C. Gonzalez, Richard E. Woods, Steven L. Eddins. Digital image processing[M]. Beijing: Electronic Industry Publishing House,2005,9:224-272.

[4] 刘华波.RGB与HSI颜色模型的转换方法对比研究[EB/OL].北京:中国科技论文在线[2008-04-30]. http://www.paper.edu.cn/releasepaper/content/200804-1063.

LIU Huabo. The RGB and HSI color model conversion method of comparative study[EB/OL]. Beijing: China Science and Technology Papers Online[2008-04-30]. http://www.paper.edu.cn/releasepaper/content/200804-1063.

[5] 王胜正,施朝健.基于两种色彩空间的颜色选择方法[J].计算机应用与软件,2004,21(2):114-116.

WANG Shengzheng, SHI Chaojian. The color selection method based on two kinds of color space[J]. Journal of Computer Applications and Software,2004,21(2):114-116.

[6] 柏春岚.Matlab在图像边缘提取中的应用[J].计算机与网络,2009,14:224-225.

BAI Chunlan. Application of Matlab in image edge detection[J]. Computer and Network,2009,14:224-225.

[7] 贺囊,晏立.基于LOG和Canny算子的边缘检测算法[J].计算机工程,2011,37(3):210-212.

HE Nang, YAN Li. Edge detection algorithm based on the LOG and Canny operator[J]. Computer Engineering,2011,5(3):210-212.

[8] 王崴,唐一平,任娟莉,等.一种改进的Harris角点提取算法[J].光学精密工程,2008,10:6-8.

WANG Wai, TANG Yiping, REN Juanli, et al. An improved Harris corner extraction algorithm[J]. Optical Precision Engineering,2008,10:6-8.

[9] 陈光,任志良,孙海柱.最小二乘曲线拟合及MATLAB实现[J].兵工自动化,2005,3:25-27.

CHEN Guang, REN Zhiliang, SUN Haizhu. Least squares curve fitting and MATLAB[J]. These Automation,2005,3:25-27.

[10] 侯超钧,曾艳姗,吴东庆,等.全局连续的分段最小二乘曲线拟合方法[J].重庆师范大学学报(自然科学版),2011,28(6):44-48.

HOU Chaojun, ZENG Yanshan, WU Dongqing, et al. Global continuous piecewise least squares curve fitting method[J]. Journal of Chongqing Normal University(Natural Science Edition),2011,28(6):44-48.

[11] 姜启源,谢金星,叶俊.数学建模[M].北京:高等教育出版社,2011:1-473.

JIANG Qiyuan, XIE Jinxing, YE Jun. Mathematical modeling[M]. Higher Education Press,2011:1-473.

中图分类号TP391.41

DOI:10.3969/j.issn.1672-9722.2016.02.034

作者简介:吴兴蛟,男,硕士研究生,研究方向:软件工程、算法设计、程序设计。吴晟,男,教授,硕士生导师,研究方向:信息安全,算法研究等。

基金项目:昆明理工大学校级项目资助。

*收稿日期:2015年8月7日,修回日期:2015年9月20日