例说用“”模型解决排列组合问题

◇山东王世双(特级教师)

解一般的排列组合题,只要用好分类、分步计数原理,掌握常见题型的解法规律就能解决之．但是,有些较为复杂的排列组合题仅仅掌握这些知识还远远不够,必须转换思维模式,利用建模进行等价转化,把问题A转化为问题B,使A中的元素个数与B中的元素个数形成一一对应关系,从而数目相同,能使一些看似较难解决的计数问题迎刃而解.

例1数列{ak}共有11项,a1=0,a11=4且|ak+1-ak|=1,k=1,2,…,10.满足这种条件的不同数列的个数有多少?

从学生解答的情况看,很多学生试图一一列出后计算出来而陷入困境．原因是不能把问题进行建模后的等价转化．此题如果建模,把问题进行以下转化,将柳暗花明．

4=a11=(a11-a10)+(a10-a9)+

(a9-a8)+…+(a3-a2)+(a2-a1).

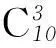
图1

例2如图1所示的5×6方格,从定点A到定点B的最短路线有多少条?

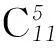
例3把10个相同的小球全部装入编号分别为1、2、3的3个盒子中,要求每个盒子中至少1个小球,则共有多少种不同的放法?

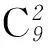
运用隔板法必须同时具备以下3个条件:1)所有元素必须相同； 2)所有元素必须分完； 3)每组至少有1个元素.

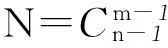
例4(例3变式)把10个相同的小球全部装入编号分别为1、2、3的3个盒子中,要求每个盒子中的小球数不小于其编号数,则共有多少种不同的方法?

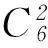
例5有3名男生、2名女生站成一排照相,其中3名男生顺序一定且2名女生的顺序一定,共有多少种排法?

例6一条街道上共有12盏路灯,为节约用电又不影响照明,决定每天晚上10点熄灭其中的4盏,并且不能熄灭相邻2盏，也不能熄灭两端的2盏,问不同熄灯方法有多少种?

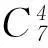
例7如图2中的A、B、C、D为某海域上的4个小岛,要建3座桥,将这4个小岛连接起来,则不同的建桥方案共有多少种?

如图3所示,构建三棱锥A-BCD,4个顶点表示小岛,6条棱表示连接任意小岛的桥梁.

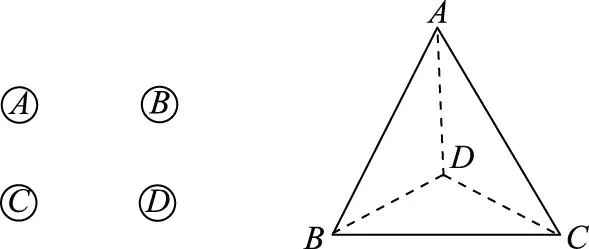
图2　　　　　　　图3

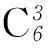
(作者单位：山东省淄博第五中学)