考虑射流掺气的改进冲刷模型

考虑射流掺气的改进冲刷模型

Rafael DuarteaLaboratory of Hydraulic Constructions (LCH), École polytechnique fédérale de Lausanne (EPFL), Lausanne CH-1015, Switzerland,*, António PinheirobCivil Engineering Research and Innovation for Sustainability (CERIS), Instituto Superior Técnico, Universidade de Lisboa, Lisbon 1049-001, Portugal, Anton J. SchleissaLaboratory of Hydraulic Constructions (LCH), École polytechnique fédérale de Lausanne (EPFL), Lausanne CH-1015, Switzerland

ar icle in fo

Article history:

Received 29 February 2016

Revised form 5 July 2016

Accepted 6 July 2016

Available online 19 September 2016

掺气

上举力

岩体冲刷

大坝安全

高速射流

岩块稳定性

冲刷评估

基于受高速射流冲击的水垫塘中掺气对岩块稳定性影响的系统试验研究，本文给出了一种基于物理特性冲刷模型的适应性研究成果。在综合冲刷模型中实现了对射流掺气模型的改进，使其得以再现有关冲刷形成的物理–机械过程，其中涉及三相，即水、岩体和空气。改进方法考虑了因挟带气泡引起的掺气射流动量减少以及射流扩散剪切层的能量消耗。岩块从岩体脱离取决于掺气的时均压强系数及修正的最大动力冲击系数的组合，对于深水垫塘中的高速射流，该系数为定值0.2。上述改进模型的模拟结果与卡里巴大坝冲坑原型观测结果吻合良好。

© 2016 THE AUTHORS. Published by Elsevier LTD on behalf of Chinese Academy of Engineering and Higher Education Press Limited Company. This is an open access article under the CC BY-NC-ND license

(http://creativecommons.org/licenses/by-nc-nd/4.0/).

1.引言

许多经验性工程方法可用来估算射流造成的下游河床冲刷。但是，此类经验方法往往只适用于具体工程，不具有广泛适用性[1]。事实上，水垫塘底板冲刷过程是由所涉及的三个因素(水、岩体和空气)相互作用的结果。此外，水流的强紊动性及其在水–岩体交界面上和岩体裂隙内部产生的压力脉动，使得水工模型中无法找到适宜的缩放比例。因此，基于弗劳德数的比尺模型，其适用性是极其有限的。

综合冲刷模型(CSM)首先由Bollaert[2]及Bollaert和Schleiss[3]提出，它的优点是考虑了下泄水流对岩体冲刷所产生的物理现象。该模型的建立是基于射流以接近原型速度冲击水垫塘底板上的封闭式和开放式裂隙的实验结果；因此，该模型再现了原型射流的压力信号特性，从而将比尺效应降到最低。此外，Manso[4]及Manso等[5]提出了对CSM的修改建议，在该建议中考虑了水垫塘底部几何形状的影响，以及相应的流态。

为了考虑从系统实验获得的射流掺气效应，本项研究提出对CSM进行调整，具体的实验设置和测试程序由Duarte[6]提出。

在洛桑联邦理工学院的水工实验室内建成了大型实验设施，垂直射流从一个直径为dj= 72 mm的喷嘴喷出，压缩空气在此喷嘴处加入水流，再现了最高速度达22.1 m·s–1的近原型掺气水流。该水流冲入直径为3 m的圆柱形水池，测试冲击射流和淹没射流特性。池内水深为Y= 30 cm、50 cm、80 cm，分别对应相对深度Y/dj为4.2、6.9和11.1。

在池底部安装一个金属系统，代表着一个全开放的3D裂隙岩体。该金属系统包含一个盒子，其中插入了一个边长为200 mm的立方块，且在立方块与盒子之间存在1 mm宽的缝隙。沿一半立方块均匀分布的12个频率为1 kHz的动水压力传感器，型号为HKM-375M-17-BAR-A。

最新的研究成果评估了气泡对于射流沿水垫塘消散和由此产生的作用于水与岩体交界面和平底板[7]以及受约束底板[8]水垫塘内缝隙处的动水压力，以及对岩块从岩体上弹射出来的影响[9]。本文结合上述前期工作，提出了工程实践上合理而又直接的方法。

2.通过考虑射流掺气对综合冲刷模型进行改进

CSM的开发建立在高速射流对岩体冲刷的理论和实验研究的基础上。冲刷过程是复杂的、连续的物理现象的结果，可分为三部分：下泄水流、水垫塘和岩体，每个部分对应CSM的一个模块，如图1所示。

在下文中，将呈现CSM的不同模块。除非另有说明，这里所说的“改进”是指所提出的对该模型适应性的修改。

2.1.下泄射流模块

下泄射流模块再现了其穿越空气的轨迹特性。射流主流轨迹符合弹道学理论。在内部紊动造成射流表面扰动增加的同时，射流形成表面掺气。水体以速度Vj射出，直径(或者在平流情况下的厚度)dj和紊动强度Tu承受下泄长度L时的重力加速度g，以速度Vi和直径di冲入水垫塘。通过增加强度来代表考虑了掺气的下泄射流，不在本项研究范围内。可查询参考文献来了解详细信息[2,3]。

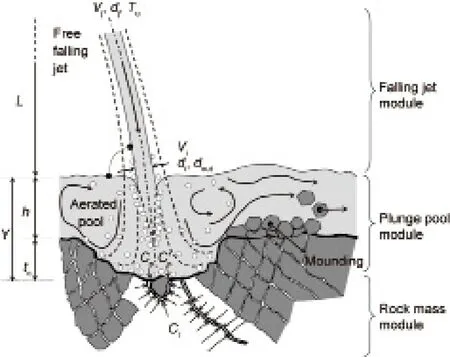
图1.形成冲刷的物理过程和主要参数的确定(改编自文献[2])。

2.2.水垫塘模块

水垫塘模块展示了射流在穿越水垫塘整个深度期间的扩散，这个过程消耗了射流一部分的能量。下泄时射流挟带大量的空气进入水垫塘，强烈影响了水流的扩散特性。射流掺气或气体与水的比例定义为Qa/Qw，其中，Qa和Qw分别代表排出的气体量和水量。可采用Ervine 等[10]提出的公式计算：

式中，K1是一个在0.2(平稳射流)和0.4(紊动射流)之间变化的参数；Ve是水垫部分射流的起始速度，高于此速度，掺气便开始，通常取值为1 m·s–1。

水垫塘气–水平均密度ρaw由下式给出：

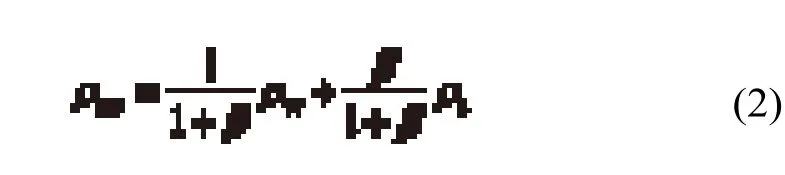
式中，ρa和ρw分别为气体和水体的密度。此过程中输入的能量由水垫体的气–水单位体积动能确定：

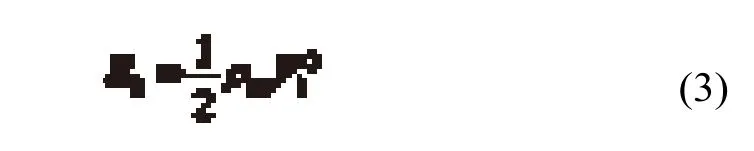
冲入水垫塘后(掺气β、平均密度ρaw、动能Ek)，射流的消散过程开始，射流在中心线处仍保持着约等于其在水垫体的速度。射流的主流按照以下表达式消失[7]：

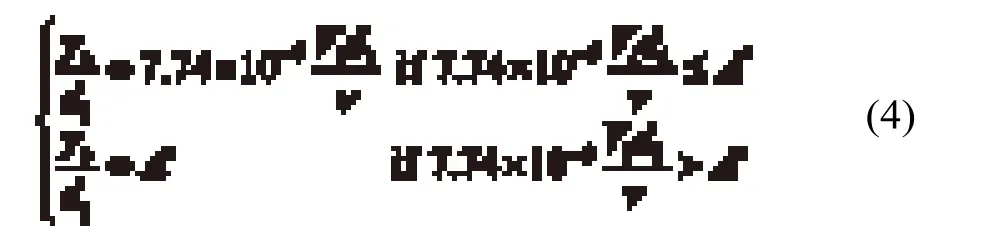
式中，yc为主流发展长度；ν为流体的运动黏滞系数；参数A′为3.5(淹没射流)和7.8(水垫塘射流)；Vidi/ν对应的是水流在水垫体的雷诺数。一旦射流主流解体，射流速度按照淹没射流和跌流的水垫塘深度线性函数衰减。

射流的剩余动能转化为作用于水垫塘底部的动水压强。时均压强pmean在射流中心线与水和岩体交界面的交点处达到最大值，即停滞。时均压强系数定义为Cp= (pmean–ρwgY)/Ek。对于停滞的无掺气射流，Cp采用下述关系式进行计算[7]：

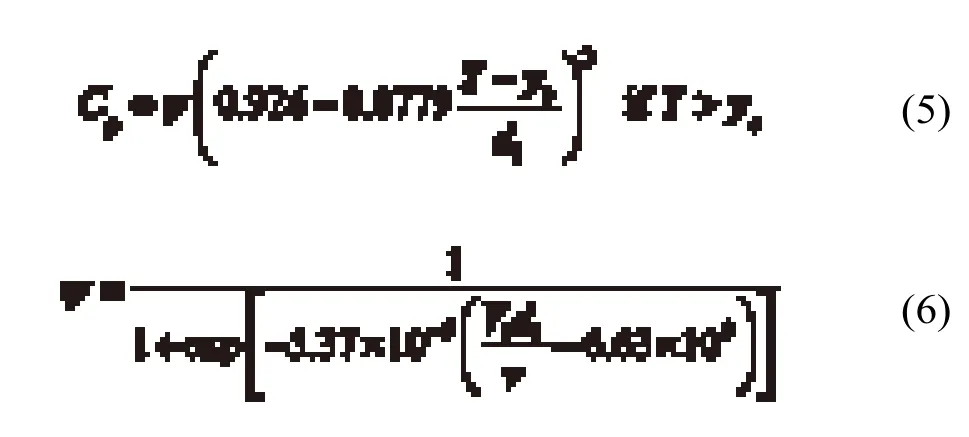
如果Y＜yc，射流主流直接冲击底部岩体，这时取Cp= 0.86。参数ψ反映了能量损失，该损失发生在射流中心线与水垫塘底部交点附近形成的撞击区域(对射流轴对称冲击的完整描述参见文献[11])。Duarte等[7]指出，ψ是射流速度的逻辑函数，对于高射流的速度，其值渐近为1。

由于气–水混合物[12,13]的平均密度减小，因此与相同流量的清水射流相比，掺气射流的动量较低。然而，Duarte等[7]指出，气泡也可以减少其与塘内水之间的剪切应力，减缓了流速衰减速度，而底部掺气射流的Cp值较高。

射流掺气β对Cp值的影响可通过淹没射流测试准确地评估，因为所有挟带的空气均在喷嘴处加入水流。图2为掺气射流的时均压力系数Cpa除以相应无掺气射流的时均压力系数Cp值，作为β的函数，可以观察到线性增加，用下式表示：

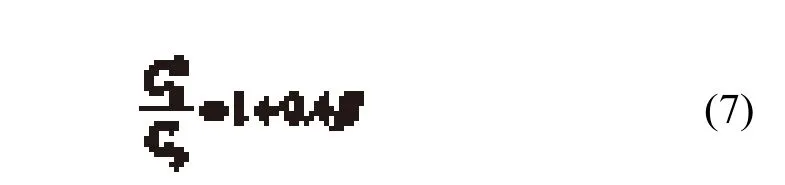
2.3.岩体模块

岩体模块再现岩石介质上发生的物理过程。这些过程包括岩体裂隙逐步破裂，随后这些破碎的岩块从水垫塘底部弹射出来。现有两种方法模拟这个过程，分别为综合断裂机械法(CFM)和动力冲击法(DI)[3]。

本项研究通过列入以不同掺气量的高速射流撞击在一个完全开放的3D裂隙处获得的实验结果来对后者进行改进。这种开放式的3D裂隙用嵌入腔内的岩块来代表，同时测量此处的动态压强和位移，并研究了固定的和移动的块体的响应。

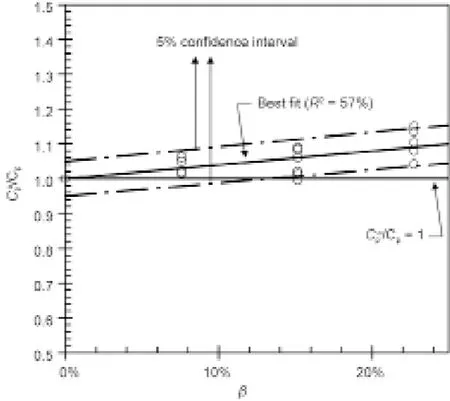
图2.掺气射流的时均压力系数Cpa除以相应无掺气射流的时均压力系数Cp与空气–水之比β的关系图。停滞淹没射流测试结果；Y/di= 9.7；射流速度Vi范围：7.4～22.1 m·s–1。

2.4.动力冲击法

动力冲击法的目的是通过射入水垫塘的水舌对底板岩块运动的能力来评估其冲刷能力[2,3]。与综合冲刷模型不同的是动力冲击法不考虑冲坑发展的时间及其演变，而是计算达到平衡状态或最终冲刷深度。

它采用的是无量纲最大动力冲击系数CImax，其定义为：给定时间段内作用在岩块上的无量纲上举力。脉冲IΔp的定义为：作用在岩块上的力的时间积分：

式中，Δp为脉冲时间；Fv为冲击射流作用在岩块周围的垂直力的总和；Fu为裂隙内因流体体积变化而产生的阻力；Wi为岩块在水中的重量；Fhf和Fsf分别为作用在岩块周围垂直裂隙上的水力和固体摩擦力；mb为岩块质量；madd为岩块附加的质量；Vb为岩块位移速度。

式(8)是根据Duarte等[9]对冲击力的详细描述做出的完整表达式。为了工程实际应用，将使用简化过的公式，即不考虑稳定力。这种简化是保守的，因为它可导致更强的降低稳定性的冲击力。此外，在实际案例中，忽略下部裂隙的体积变化所引起的流体阻力也是现实的。Duarte等[9]在实验装置上模拟岩块的运动时，这种影响非常重要。但是，在原型条件下，随着即时水力压裂引起的裂隙逐渐加宽，水流可快速填充，而实验设施展现的情况并非如此。所得到的表达式等同于由Bollaert和Schleiss[3]提出的公式：

只要有净上举力存在，就需要考虑冲击IΔp。试验中的最大冲击为Imax。时间除以裂隙内压力波周期变成无量纲的Tp=2Lf/c，其中，Lf是裂隙长度，c是波速[3]。为简单起见，假定岩块底部是方形，边长为xb，高z，因此，Lf= 2z+xb。将冲击力转化成无量纲的、作用于岩块一个面上的压力(在本案例中为岩块的顶部或底部，面积为

xb

2)，然后再除以单位体积上的动能Ek。最大动力冲击系数CImax采用下式计算：

CImax的实验结果在图3中表示为出口射流掺气β1的函数，在图4中表示为入塘水流速度Vaw的函数，在图5中表示为水垫塘相对深度Y/dj的函数。

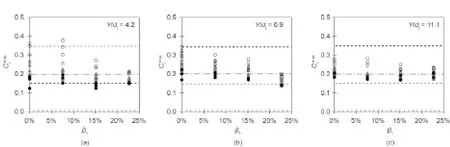
图3.最大冲击动力系数CImax与出口射流掺气β1的实验结果。(○)Vaw= 12.3 m·s–1；(∆)Vaw= 14.7 m·s–1；(▲)Vaw= 17.2 m·s–1；(●)Vaw= 19.6 m·s–1；(♦)Vaw= 22.1 m·s–1；a)Y/dj= 4.2；b)Y/dj= 6.9；c)Y/dj= 11.1。CImax在0.15～0.35之间变化，平均值为0.20(虚线)。

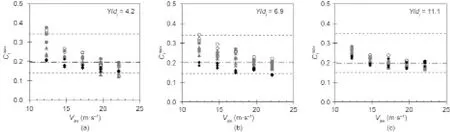
图4.最大冲击动力系数CImax与出口射流速度Vaw的实验结果。(○)β1= 0 %；(●)β1= 8 %；(▲)β1= 15 %；(♦)β1= 23 %；a)Y/dj= 4.2；b)Y/dj= 6.9；c)Y/dj= 11.1。CImax在0.15～0.35之间变化，平均值为0.20(虚线)。

CImax的最大值和最小值分别约为0.35和0.15。射流掺气β1的影响相对较小，并且β1的高值会降到接近0.20(图3)。通过分析出口射流速度的影响(图4)，可以看到，对于高速射流的速度，CImax朝0.2平滑衰减。在图5中，向0.2收敛也可看作是水垫塘内水体相对深度的函数，其中，不同的射流掺气结果向较深的水垫塘的平均值靠拢。因此，基于实验结果，建议使用CImax= 0.2，与原型条件下的充分掺气高速射流相对应。

最后，在水垫塘底部脱落岩块的最大冲击动力取决于塘内水流动能的消耗以及作用在岩块上的最大冲击系数。前者由时均压力系数Cpa来表示，它考虑了掺气的影响。最大动力冲击和岩块的垂直位移用下面的表达式进行计算：

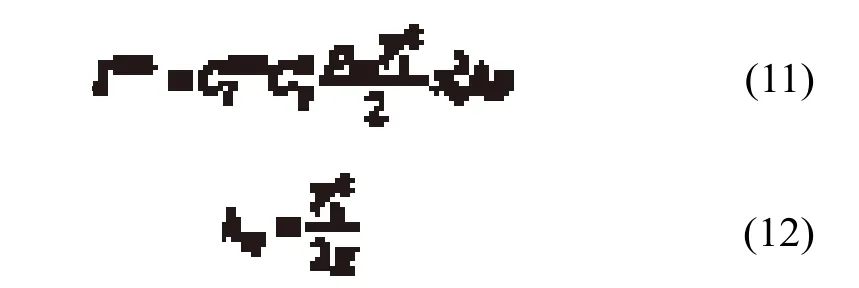
这种改进方法不同于Bollaert和Schleiss[2,3]的建议，他们提出的最大冲击值完全取决于CImax，而不是式(11)中的CImax和Cpa。在实验结果的基础上，他们提出了CImax作为水垫塘相对深度递减函数的经验关系式：

图5.最大冲击动力系数CImax与水垫塘相对深度Y/dj的实验结果。(○)β1=0 %；(●)β1=8 %；(▲)β1=15 %；(♦)β1=23 %。虚线表示外边界和平均值。

本项研究提出的方法中，Cpa是水垫塘相对深度的递减函数。式(5)和式(6)反映了无掺气射流沿着水垫塘消散的情况。由气泡夹带引起的速度衰减降低而导致的压力升高在式(7)中用Cpa表示。另外，式(11)中射流的低动能再现了由于掺气射流表现密度较低引起的压力降低。

3.案例分析：卡里巴大坝下游冲刷坑

3.1.概况

卡里巴大坝位于赞比亚和津巴布韦之间的界河——赞比西河上，是世界上最大的人工水库之一。电站的装机容量为1266 MW，现已对电厂进行了更新改造，将装机容量提高至1450 MW[14,15]。该电站由赞比西河管理局(ZRA)负责运行管理。泄洪设施包括6个泄洪中孔，单孔泄流量为1500 m3·s–1。除了坝身泄洪口外，没有其他泄洪设施(图6)。

由于1959年工程建成后就开始泄洪，长期的运行导致大坝下游水垫塘底部形成了深而陡的冲坑。1981年水下地形测量结果显示水垫塘底部最低冲坑高程为306 m a.s.l.(图7)，2001年的冲坑高程也大致如此，由此推测当前水垫塘底部的形状变化不大，即低于正常尾水位约80 m，低于原始河床70 m。

采用物理模型试验和CSM数值模型相结合建立一个组合模型，以便找到能保持冲坑稳定的解决方案[16,17]，主要关注的是防止朝坝趾方向的进一步淘刷。为此，计划进行水下开挖，改变水垫塘底部的形状，降低岩体处的压力波动，并将转向的水流导向下游[14]。

图6.2010年4月卡里巴大坝间隔开启3孔泄洪的下游视图(B. Goguel提供)。

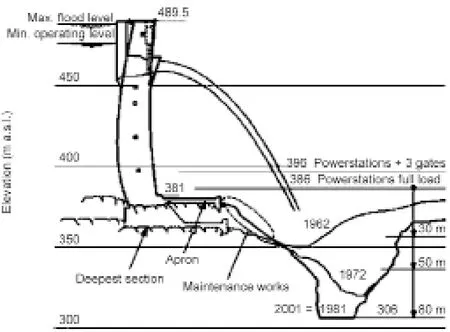
图7.卡里巴水垫塘冲坑[14]随时间发展演变情况的纵剖面。

3.2.用改进DI法估算岩体冲刷

主要的输入参数和中间结果见表1。射流以Vi= 41.4 m·s–1的速度到达水垫塘表面，挟带大量空气进入水垫塘(Ca=48%)。形成的射流主流长度达49.1 m，到达水垫塘底部。

根据Duarte等[8]对高度掺气的高速射流的研究结果，岩体裂隙内部的压力波速选为70 m·s–1。结果发现，压力波速因空气含量和岩块振动而大幅降低，与流体边界的伪弹性表现相符。

事实上，水与岩体交界面处的岩块周围裂隙由于射流引起的水力压裂逐渐加宽，使得坑内岩块振动越来越大。正如Duarte等[8]所指出的，这些振动与掺气效应共同作用降低了压力波速。此外，Duarte等[9]指出，在岩块上升的同时，节理的开度有利于水流充填裂隙，反之亦然，从而减少裂隙内水流因体积变化引起的阻力。这一结果正好为式(9)中所考虑的忽略稳定力的简化假设提供了支撑。

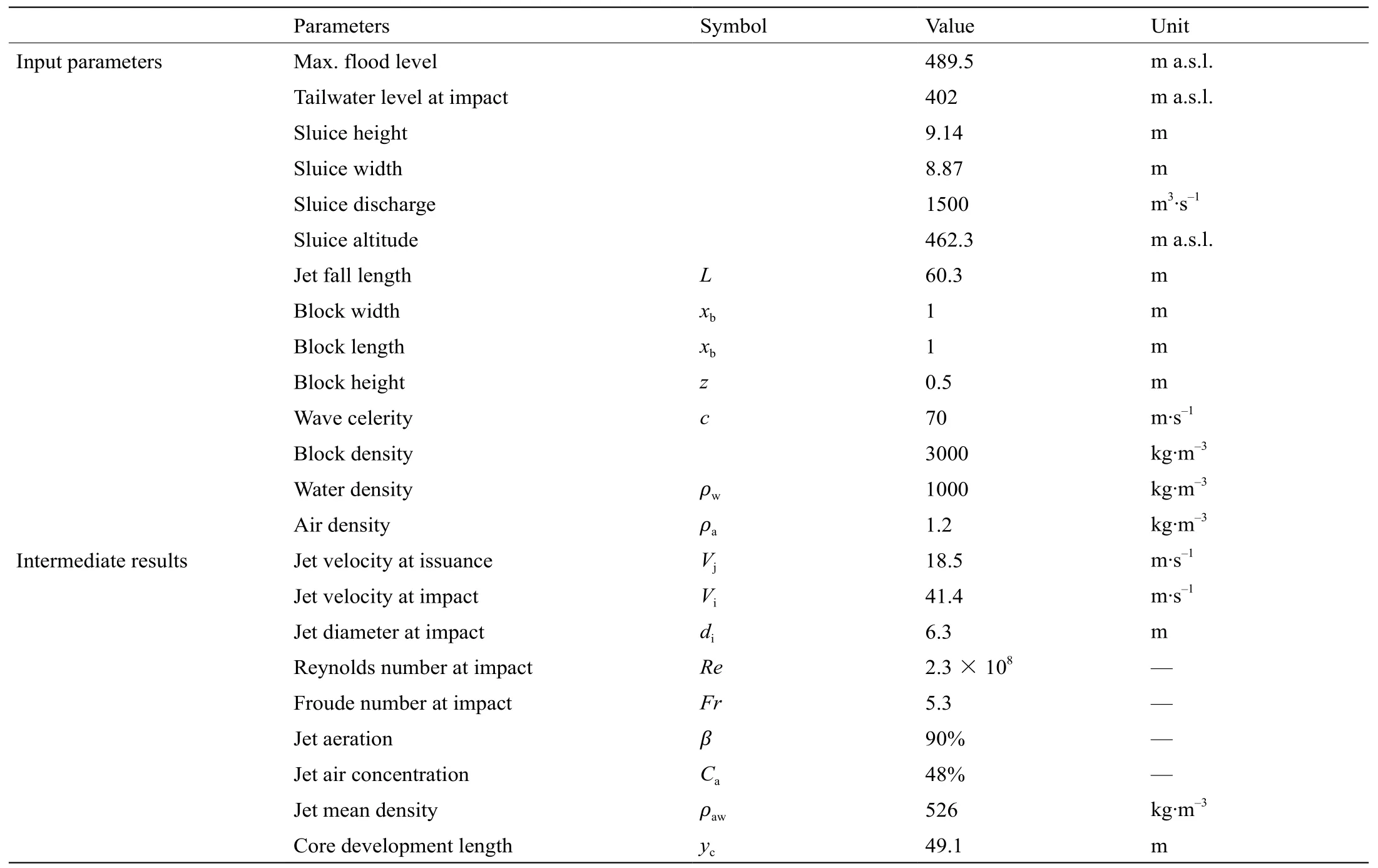
表1.改进DI法中使用的参数

地质勘测表明，岩体由质量非常好的新鲜的和蚀变片麻岩(150～200 MPa)组成。岩体有垂直和倾角约20°～30°[17]的次水平节理组。

对于岩块从岩体中弹射出来的问题，文献中采用了不同的标准：临界参数hup/z，决定岩腔内岩块的位移程度，Bollaert [2]用hup/z =1确定阈值，低于该阈值则岩块稳定；之后，Bollaert和Schleiss [3]假定对hup/z ＞ 0.2存在一个中间区域，在此区间岩块振动，低于此限度则水垫塘稳定。

近来，Asadollahi等[18]以破裂岩体介质的岩块弹射为依据进行了岩石冲刷研究。他们开发了一种迭代算法，即三维岩体稳定性(BS3D)，该算法已经由Federspiel[19]的实验数据进行了验证。Asadollahi等[18]认为，如果岩块的位移大于岩块高度的四分之一，则岩块最容易从塘底岩体中起动。

表2所示为用改进动力冲击法计算的极限冲刷深度结果，这些结果是以破坏标准hup/z=1或0.25为依据计算出来的；并与1972年和1981年测得的纵剖面图进行了对比，见图8。

两个破坏标准之间的差别不大。此外，最终的冲刷深度结果与1981年和2001年测量的塘底最深点接近。事实上，破坏标准hup/z = 0.25导致完全相同的塘底高程，即306 ma.s.l.。这表明，从冲击射流将岩块从岩体中弹出的能力的角度来考虑，冲坑已达到了极限。

为了进行比较，使用破坏标准hup/z = 0.25的原始DI方法得出底部高程为289.5 ma.s.l.。而且，如果将这些结果与Mason和Arumugam[20]提出的具有恒定参数的经验公式进行比较，可以看出：

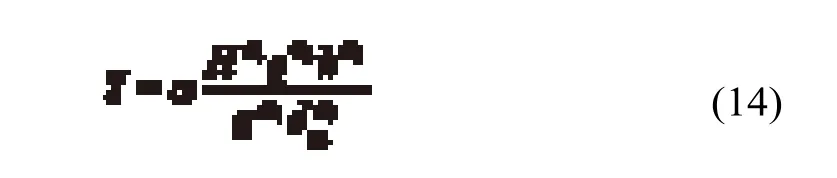
式中，H为由库水位和尾水位之间的高差所确定的水头；q为流量比；dm为颗粒或岩石的平均尺寸；α = 3.27，α1= 0.05，α2= 0.60，α3= 0.15，α4= 0.30，α5= 0.10；计算得出的冲坑最低点高程为338.8 m a.s.l.，远高于目前高程。此外，如果用Mason和Arumugam[20]的两个模型和原型数据所获得的可变参数，并用式(14)进行计算，则结果显示水垫总深度只有1.5 m，说明在本案例中参数超出了范围。此示例证明，经验公式很少可以代表复杂的原型情况，只有基于物理原理的表达式才可以精确地估计冲刷情况。

表2.于改进DI法得到的最终冲刷深度的数值结果

然而，在作出这些说明时必须非常小心，因为还要对其他方面进行分析。必须注意的是，DI法仅考虑射流的紊动剪切层的侵蚀能力；换句话说，DI法仅考虑了射流直接冲击的影响，并没有考虑对射流转向形成的旋滚的影响。

图8.应用改进动力冲击(DI)法计算卡里巴大坝冲坑的结果。灰色实线为1972年测得的冲坑轮廓；黑灰色线为1981年测量的冲坑轮廓，与2001年测量的相同；黑虚线为改进DI法，hup/z = 1或hup/z = 0.25；灰虚线为原DI法，hup/z = 0.25。

如Manso等[5]所强调的，水垫塘底部的几何形状会产生特定的水流流态，并且对射流在塘底消散和转向的方式有很大的影响。射流冲击到其中心线与水和岩石交界面交叉处后随即发生转向，形成平行于底部的壁面射流。壁面射流也具有冲刷潜力[21,22]，如前所述，在上述DI法中并未提及。在卡里巴的这个案例中，朝冲击点上游的射流转向是一个需要特别关注的问题，它可能会导致向坝基方向的淘刷。目前重塑塘底形状的工作目标是引导冲击射流转向下游，从而避免冲刷坑向大坝方向发展。通过采取预挖的措施，估计冲刷坑不会进一步加深[14,16,17]。

模型中使用的参数也产生其他不确定性，如它高度依赖于所考虑的波速。虽然本案例中所使用的波速是实验的可靠结果，但在将来该研究可以扩展，用于评估岩块的几何形状(相对于射流和水垫塘几何尺度)，以及节理连锁对波速的影响。而且，作为工程应用的简化假设，通过忽略移动岩块的稳定力对岩块受到的动力冲击进行计算。

改进的DI法能够模拟射流掺气量的变化。虽然卡里巴大坝案例用的都是假设，射流掺气对最大冲刷深度的影响如图9所示。所用的破坏标准是hup/z= 0.25。对掺气浓度的增加进行了模拟，从现有射流的估值48 %提高到大约65%。

图9显示的结果表明，射流掺气能减少冲刷。底部高程随着挟带空气浓度的增加而稳定升高，但是高程变化不大。模拟掺气浓度增加17 %，最大冲刷深度只减少2.1 m，底部高程由306 m a.s.l.提高至308.1 m a.s.l.。

4.结论

对最初由Bollaert和Schleiss[2,3]建立的基于物理基础的冲刷模型做了改进，利用接近原型速度射流的系统实验考虑了射流掺气的影响。所提出的修改模型中，综合冲刷模型是评估射流导致下游岩体冲刷的唯一的工程方法，它是根据水工模型实验，考虑基于物理–力学的射流全过程, 涉及三相，即水、岩石和空气。

改进包括作用在水与岩体交界面上的时均压力，作为水垫塘中消能的结果, 该压力受掺气的影响很大。这些压力用掺气时均压力系数表示，它考虑了气水混合物密度降低以及掺气射流在水垫塘中的消散减弱的因素，从而将Duarte等[7]的最新研究成果也考虑在内。

此外，提出对作用于水垫塘底部脱落岩块上的动力冲击特性模型进行改进。这一特征被表示为最大动力冲击系数，实验表明其值约等于0.2，特别是对于高速射流冲入深水垫塘的情况。最后，作用在岩块上的冲击力受掺气时均压力系数和最大动力冲击系数的综合影响。

卡里巴大坝冲刷坑案例研究表明，模拟的冲刷坑最低高程值接近于1981年和2001年的实测结果。具体地说，如果破坏标准是一旦岩块的四分之一高度脱离所处的腔体时，岩块就会被弹出，那么计算所得的最终冲刷深度与实测的冲坑底高程(306 m)一致。然而，动力冲击法(DI)只考虑了冲击射流的冲刷能力，未考虑其他冲刷机理，比如由于作用于水与岩石交界面的冲击射流发生转向而产生的壁面射流。

对该模型的进一步改进包括岩块尺寸相对于射流尺寸的影响，以及其对诸如波速和最大动力冲击等参数的影响。另外，进行更多的案例研究有助于将改进的模型应用于工程实践。

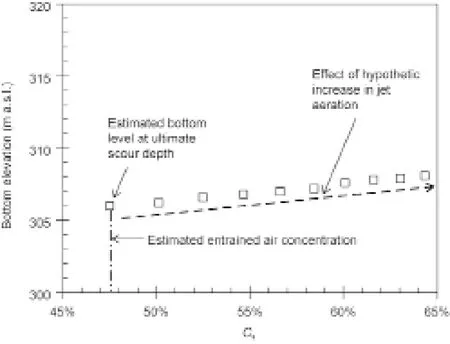
图9.卡里巴大坝最大冲刷深度冲坑底高程与掺气浓度Ca的关系。(□)模型结果；黑色虚线箭头为结果趋势；用改进DI法的计算结果，hup/z= 0.25。

致谢

本研究项目由葡萄牙科学与技术基金会(FCT，葡萄牙，批准号SFPH/BD/51074/2010)和LCH - EPFL资助。

Compliance with ethics guidelines

Rafael Duarte, António Pinheiro, and Anton J. Schleiss declare that they have no conflict of interest or financial conflicts to disclose.

[1] Bollaert E, Schleiss A. Scour of rock due to the impact of plunging high velocity jets Part I: a state-of-the-art review. J Hydraul Res 2003;41(5):451—64.

[2] Bollaert E. Transient water pressures in joints and formation of rock scour due to high-velocity jet impact [EPFL PhD thesis n° 2548 and LCH communication n° 13]. Lausanne: Ecole polytechnique fédérale de Lausanne; 2002.

[3] Bollaert E, Schleiss A. Physically based model for evaluation of rock scour due to high-velocity jet impact. J Hydraul Eng 2005;131(3):153—65.

[4] Manso PA. The influence of pool geometry and induced flow patterns in rock scour by high-velocity plunging jets [EPFL PhD thesis n° 3430 and LCH communication n° 25]. Lausanne: Ecole polytechnique fédérale de Lausanne; 2006.

[5] Manso PA, Bollaert E, Schleiss A. Influence of plunge pool geometry onhigh-velocity jet impact pressures and pressure propagation inside fissured rock media. J Hydraul Eng 2009;135(10):783—92.

[6] Duarte R. Influence of air entrainment on rock scour development and block stability in plunge pools [EPFL PhD thesis n° 6195 and LCH communication n° 59]. Lausanne: Ecole polytechnique fédérale de Lausanne; 2014.

[7] Duarte R, Schleiss A, Pinheiro A. Influence of jet aeration on pressures around a block embedded in a plunge pool bottom. Environ Fluid Mech 2015;15(3):673—93.

[8] Duarte R, Schleiss A, Pinheiro A. Effect of pool confinement on pressures around a block impacted by plunging aerated jets. Can J Civil Eng 2016;43(3):201—10.

[9] Duarte R, Pinheiro A, Schleiss A. Dynamic response of an embedded block impacted by aerated high-velocity jets. J Hydraul Res 2016;54(4):399—409.

[10] Ervine DA, Falvey HT, Withers W. Pressure fluctuations on plunge pool floors. J Hydraul Res 1997;35(2):257—79.

[11] Beltaos S, Rajaratnam N. Impingement of axisymmetric developing jets. J Hydraul Res 1977;15(4):311—26.

[12] Manso PA, Fiorotto V, Bollaert E, Schleiss A. Discussion of “Effect of jet air content on plunge pool scour” by Stefano Canepa and Willi H. Hager. J Hydraul Eng 2004;130(11):1128—30.

[13] Ervine DA, Falvey HT. Behaviour of turbulent water jets in the atmosphere and in plunge pools. Proc Inst Civil Eng 1987;83(1):295—314.

[14] Noret C, Girard JC, Munodawafa MC, Mazvidza DZ. Kariba dam on Zambezi River: stabilizing the natural plunge pool. La Houille Blanche 2013;(1):34—41. French.

[15] Tapfuma V, Mazvidza D, Goguel B, Molyneux JD. Kariba Dam safety monitoring and resulting maintenance works. In: Proceedings of the 18th ICOLD Congress; 1994 Nov 7—11; Durban, South Africa. Paris: International Commission on Large Dams; 1994. p. 1445—64.

[16] Bollaert E, Duarte R, Pfister M, Schleiss A, Mazvidza D. Physical and numerical model study investigating plunge pool scour at Kariba Dam. In: Proceedings of the 24th Congress of CIGB—ICOLD; 2012 Jun 2—8; Kyoto, Japan. Paris: International Commission on Large Dams; 2012. p. 241—8.

[17] Bollaert E, Munodawafa MC, Mazvidza DZ. Kariba Dam plunge pool scour: quasi-3D numerical predictions. La Houille Blanche 2013;(1):42—9.

[18] Asadollahi P, Tonon F, Federspiel MPEA, Schleiss A. Prediction of rock block stability and scour depth in plunge pools. J Hydraul Res 2011;49(6):750—6.

[19] Federspiel MPEA. Response of an embedded block impacted by high-velocity jets [EPFL PhD thesis n° 5160 and LCH communication n° 47]. Lausanne: Ecole polytechnique fédérale de Lausanne; 2011.

[20] Mason PJ, Arumugam K. Free jet scour below dams and flip buckets. J Hydraul Eng 1985;111(2):220—35.

[21] Bellin A, Fiorotto V. Direct dynamic force measurement on slabs in spillway stilling basins. J Hydraul Eng 1995;121(10):686—93.

[22] Fiorotto V, Rinaldo A. Turbulent pressure fluctuations under hydraulic jumps. J Hydraul Res 1992;30(4):499—520.

* Corresponding author.

E-mail address: rafael.duarte@alumni.epfl.ch

2095-8099/© 2016 THE AUTHORS. Published by Elsevier LTD on behalf of Chinese Academy of Engineering and Higher Education Press Limited Company.

This is an open access article under the CC BY-NC-ND license (http://creativecommons.org/licenses/by-nc-nd/4.0/).

英文原文: Engineering 2016, 2(3): 294—301

Rafael Duarte, António Pinheiro, Anton J. Schleiss. An Enhanced Physically Based Scour Model for Considering Jet Air Entrainment. Engineering,

http://dx.doi.org/10.1016/J.ENG.2016.03.003