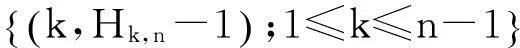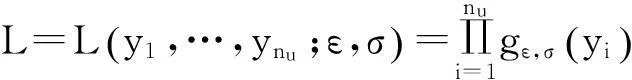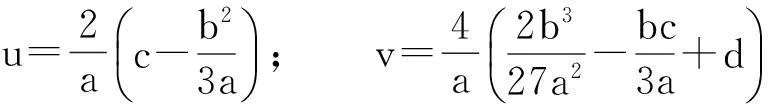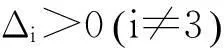边坡位移预警指标的实时估计与诊断
任 杰,苏怀智,杨 孟,周志杰
(1. 河海大学水文水资源与水利工程科学国家重点实验室,江苏南京 210098; 2. 河海大学水利水电学院,江苏南京 210098)
边坡位移预警指标的实时估计与诊断
任杰1,2,苏怀智1,2,杨孟1,2,周志杰2
(1. 河海大学水文水资源与水利工程科学国家重点实验室,江苏南京210098; 2. 河海大学水利水电学院,江苏南京210098)
摘要:边坡预警指标的实时估计与诊断是实现边坡安全监控、预防边坡演变为滑坡的重要手段。安全预警注重考虑极端事件,其关键在于能否准确进行效应量序列分位数分析及刻画其尾部特征。基于极值理论中超阈值(Peaks over Threshold, POT)模型,分时段考虑边坡位移监测序列,借助Hill图法拟定合理的阈值,再利用广义帕累托分布(Generalized Pareto Distribution, GPD)对超阈值序列进行拟合分析,渐进地刻画位移序列分布的尾部特征,分析其抵御已经历荷载的能力。假定边坡失事概率,得到位移预警指标实时估计序列,挖掘或评估出该边坡面临可能发生极端荷载时的抵御能力。最后基于突变理论中尖点突变模型对位移预警指标实时估计序列进行突变诊断,结合具体边坡工程实例,验证了POT-突变理论混合模型的合理性。
关键词:边坡; 位移预警指标; 极值理论; POT模型; 尖点突变理论
根据边坡工程性态及原始监测资料,借助先进的数学、力学工具建立各种效应量的预警指标估计模型,是实现边坡工程安全预警的重要手段。边坡工程安全预警的主要目的在于通过实时监测并分析边坡变形及发展态势,以便能及时采取工程或非工程措施,达到防止或减少边坡破坏所带来的灾害损失。对边坡效应量预警指标的估计是实现边坡安全预警的前提[1]。预警机理在于对抵御已经历荷载能力的分析,评估和预测抵御可能发生荷载的能力。预警指标估计重点考虑极端事件,借助极值理论可实现对其的估计和研究[2]。
本文基于极值理论中POT模型进行建模。其流程通常是依据一定的规则拟定合理的阈值,以超阈值序列作为子样本序列,利用GPD分布拟合子样本序列,得到其分布函数,根据统计学条件概率公式继而得到母样本的分布函数,结合边坡失事概率完成对预警指标的估计。A. A. Balkema以及J. Pickands等指出,来自同一总体的简单随机样本,若阈值拟定充分大,超阈值的随机变量的极限分布即为GPD分布[3-4]。大量学者研究表明,基于POT模型的极值理论方法在扩大样本容量,提高样本质量的同时比其他方法能够更准确地描述序列分布的尾部特征,尤其在采样数据较少的情况下,是一种较为准确的分位数分析和预测手段[2,5-7]。
通过对不同时段位移监测序列进行POT建模分析,得到预警指标实时估计序列,再利用尖点突变理论对其变化趋势进行性态突变诊断,结合某边坡工程实例,对该法的合理性进行了验证。
1边坡位移预警指标估计极值POT模型
1.1GPD分布与POT模型
利用GPD分布拟合超阈值序列来渐进地刻画分布的尾部特征是建立POT模型的基础。GPD分布定义为:
(1)
式中:ε为形状参数;当ε≥0时,x≥0;当ε<0时,u 1.2超阈值分布函数(CEDF)和总体分布函数 (2) 式中:0≤y 根据条件概率公式,可得总体分布函数: (3) (4) (5) 1.3位移监测序列厚尾检验 1.4阈值u拟定的Hill图法 利用GPD分布拟合超阈值序列,需解决阈值u拟定这个关键问题,同时阈值u也是准确估计参数ε和σ的前提。若阈值u的拟定过高,超阈值序列样本容量少,使得参数估计的方差过大;若阈值u的拟定过低,则有可能不满足PBDH定理成立的条件,使得超阈值序列样本分布与GPD分布产生较大差异。阈值拟定方法分作图法与数值计算法两类[6,9]。本文借助Hill图法进行阈值u的拟定。 (6) 1.5GPD分布参数估计 GPD分布参数估计的方法有极大似然估计法、概率权矩法以及L矩估计法等。本文采用最常用的极大似然估计法对GPD分布参数进行估计。 (7) (8) (9) 至此,根据上文公式及计算所得参数便可确定式(5)的分布函数。据分布函数反函数,结合边坡失事概率,可以求得边坡位移预警指标估计值。 2边坡位移预警指标性态诊断突变理论 2.1尖点突变模型 突变理论是以奇点理论、稳定性理论等数学理论为基础,用以研究微积分方法不能解释的不连续变化现象的理论[11-12]。突变理论通过给出系统在突变过程的势函数,研究其突变流形和分叉集进而确定系统所属状态。根据边坡失稳特征,采用尖点突变模型判别其稳定性[13-14]。 (10) 式中:x为边坡状态变量;u,v为边坡控制变量。 (11) 突变流形的实根个数由下式Δ符号判断:Δ=8u3+27v2 (12) Δ>0时有一个实根,边坡处于稳定状态;Δ<0时有3个互异实根,边坡处于非稳定状态;Δ=0时,边坡处于临界状态。 2.2边坡预警指标尖点突变模型 本文采用经验方法[11,13]建立尖点突变模型。对于边坡预警指标估计序列,采用最小二乘法进行数据拟合,得到突变流形结果如下式所示: (13) (14) (15) 计算所得u和v,代入式(12)中可计算Δ,进而判别预警指标序列的稳定状态。分析过程中,往往需确定突变点位置,本文借鉴文献[15]的方式确定出在何时发生了突变。年份为ti时,取前i年的预警指标估计序列进行式(13)~(15)计算,并获取Δi,当Δi=0时,所对应年份即为突变发生临界年份,若前i年数不足以进行式(13)拟合,则通过线性插值使点数增加。 3边坡工程实例 为阐述建模方法,验证模型可靠性,本文以黄河流域某边坡工程为例,依据该边坡某测点2009—2013年垂直方向位移监测数据,以年为区间,获得2009年73个监测数据,2010年170个监测数据,2011年165个监测数据,2012年261个监测数据,2013年70个监测数据,结合边坡实际情况及上下游区域概况,依经验[2,16-17]假定该边坡失事概率为1%,依前文建模方法,得到位移预警指标估计值,并对预警指标估计值序列进行突变诊断。考虑到监测数据具有非等时距性,为平缓数据,本文以该测点垂直位移日变化量(向下取正,单位:mm/d)为研究对象。 3.1监测数据厚尾检验 2009—2013年监测数据厚尾检验见图1。由图1可知,监测数据中间部分近似直线,呈微凹型,下端翘起,具有厚尾分布,满足极值POT模型成立的前提条件。 图1 2009—2013年监测数据厚尾检验Fig.1 Heavy-tailed tests for monitoring data of 2009—2013 3.2Hill图法拟定阈值u 根据1.4节中阈值的拟定方法,绘出2009—2013年Hill曲线图(见图2),确定相应年份阈值。 根据Hill图中数据变化急缓情况,并结合已有学者文献[10]的研究,拟定每年的k值,并由k值得到对应的阈值u,假定边坡失事概率为1%,由式(6)计算F(x)反函数,得到预警指标估计值序列。结合年极值,将结果列于表1。为便于分析与比较,据表1绘制图3。 图2 2009—2013年Hill图Fig.2 Hill figures of 2009—2013 图3 预警指标估计序列与极值序列对比Fig.3 Comparison between sequences of early warning indicator and extreme value 参数2009年2010年2011年2012年2013年k612163314u(mm·d-1)32.7631.5014.906.702.50位移预警指标估计值(mm·d-1)41.3337.1437.2918.506.75年极值(mm·d-1)41.0737.4022.4013.004.60 3.3尖点突变模型诊断预警指标估计值序列 3.4结论 据表1、图3及Δi的计算结果可以看出: (1)2009—2013年期间阈值、预警指标估计值以及极值都呈下降趋势,反应边坡向安全性态发展; (2)2009—2010年间,该边坡的位移预警值略小于年极值,该边坡处于危险状态,2010年以后,预警值均高于年极值,该边坡处于安全状态; (3)2011年时,状态判别式Δ≈0,说明位移预警指标估计值序列处于临界状态,任之发展,将会发生突变,即Δ<0,之后却发现Δ>0,显而易见,边坡位移预警指标估计值向好的方向发生了转变。2009年发现,该边坡位移变化呈增大趋势,便通过控制水库水位升降、边坡处理等工程措施加以控制,突变理论印证了采取控制措施后取得了实质性效果。 4结语 极值理论POT模型以超阈值序列的GPD分布特征为研究对象,全面地考虑了所有较大测值,更好地刻画了数据样本的超阈值分布特征,因此得到的预警指标估计值能更客观地反映工程实际。 本文将基于极值理论的POT模型应用于边坡位移预警指标估计中,通过分析研究,该边坡处于安全状态,并通过突变理论印证了控制措施起到了实质性作用,这与边坡实际情况较为吻合,与该边坡实际监测资料成果分析一致。研究分析表明极值POT模型与突变诊断模型相结合应用于边坡位移预警指标估计与诊断上具有一定的科学性,较为可靠。 本文中边坡失事概率尚无具体规范可依,依经验对其假定,具有主观性;监测数据具有时间间隔性,为平缓数据使其满足GPD分布,仅做了平均处理;建立POT模型的过程中,为简化分析,仅考虑超阈值序列数值大小而忽略超阈值序列的时间效应。为更加客观地估计预警指标,存在的这些不足,需进一步进行研究与完善。 参考文献: [1]张振华,冯夏庭,周辉,等. 基于设计安全系数及破坏模式的边坡开挖过程动态变形监测预警方法研究[J]. 岩土力学, 2009, 30(3): 603- 612. (ZHANG Zhen-hua, FENG Xia-ting, ZHOU Hui, et al. Research on dynamic early warning method of slope deformation monitoring during excavation based on design safety factor and failure mode[J]. Rock and Soil Mechanics, 2009, 30(3): 603- 612. (in Chinese)) [2]苏怀智,王峰,刘红萍. 基于POT模型建立大坝服役性态预警指标[J]. 水利学报, 2012, 43(8): 974- 978, 986. (SU Huai-zhi, WANG Feng, LIU Hong-ping. Early-warning index for dam service behavior based on POT model[J]. Journal of Hydraulic Engineering, 2012, 43(8): 974- 978, 986. (in Chinese)) [3]BALKEMA A A, DE HAAN L. Residual life time at great age[J]. Annals of Probability, 1974(2): 792- 804. [4]PICKANDS J. Statistical inference using extreme order statistics[J]. Annals of Statistics, 1975(3): 119- 131. [5]花拥军,张宗益. 极值BMM与POT模型对沪深股市极端风险的比较研究[J]. 管理工程学报, 2009, 23(4): 104- 108, 115. (HUA Yong-jun, ZHANG Zong-yi. Comparative research on extreme risk of stock market based on BMM and POT model[J]. Journal of Industrial Engineering and Engineering Management, 2009, 23(4): 104- 108, 115. (in Chinese)) [6]陈红英. POT模型在巨灾保险中的应用[D]. 上海: 上海交通大学, 2010.(CHEN Hong-ying. Application of POT model to catastrophe insurance[D]. Shanghai: Shanghai Jiaotong University, 2010. (in Chinese)) [7]钱小仕,王福昌,盛书中. 基于广义帕累托分布的地震震级分布尾部特征分析[J]. 地震学报, 2013, 35(3): 341- 350. (QIAN Xiao-shi, WANG Fu-chang, SHENG Shu-zhong. Characterization of tail distribution of earthquake magnitudes via generalized Pareto distribution[J]. Acta Seismologica Sinica, 2013, 35(3): 341- 350. (in Chinese)) [8]边宽江,程波,王蕾蕾. 收益分布尖峰厚尾问题的统计检验[J]. 统计与决策, 2009(7): 83- 85. (BIAN Kuan-jiang, CHENG Bo, WANG Lei-lei. Problems about peak and fat-tail of income distribution based on statistics test[J]. Statistics & Decision, 2009(7): 83- 85. (in Chinese)) [9]HILL B M. A simple general approach to inference about the tail of a distribution[J]. Annals of Mathematical Statistics, 1975, 3(5): 1163- 1174. [10]LORETAN M, PHILLIPS P C B. Testing the covariance stationarity of heavy-tailed time series: an overview of the theory with applications to several financial datasets[J]. Journal of Empirical Finance, 1994, 1(2): 211- 248. [11]凌复华. 突变理论及其应用[M]. 上海: 上海交通大学出版社, 1987. (LING Fu-hua. Catastrophe theory and its application[M]. Shanghai: Shanghai Jiaotong University Press, 1987.(in Chinese)) [12]阿诺德. 突变理论[M]. 周燕华, 译. 北京: 高等教育出版社, 1990. (ARNOLD V I. Catastrophe theory[M]. Translated by ZHOU Yan-hua. Beijing: Higher Education Press, 1990. (in Chinese)) [13]姜璐,于连宇. 初等突变理论在社会科学中的应用[J]. 系统工程理论与实践, 2002(10): 113- 117. (JIANG Lu, YU Lian-yu. The application of primary catastrophe theory to social science[J]. Systems Engineering-Theory & Practice, 2002(10): 113- 117. (in Chinese)) [14]丁晓唐,顾冲时,蒋勇. 基于有限元和突变理论的高拱坝坝体稳定研究[J]. 河海大学学报:自然科学版, 2008, 36(2): 175- 178. (DING Xiao-tang, GU Chong-shi, JIANG Yong. Analysis of stability of high arch dams based on FEM and catastrophe theory[J]. Journal of Hohai University(Natural Sciences), 2008, 36(2): 175- 178. (in Chinese)) [15]郑东健,雷霆. 基于突变理论的高拱坝失稳判据研究[J]. 岩土工程学报, 2011, 33(1): 23- 27. (ZHENG Dong-jian, LEI Ting. Instability criteria for high arch dams using catastrophe theory[J]. Chinese Journal of Geotechnical Engineering, 2011, 33(1): 23- 27. (in Chinese)) [16]雷鹏,常晓林,肖峰,等. 高混凝土坝空间变形预警指标研究[J]. 中国科学:技术科学, 2011, 41(7): 992- 999. (LEI Peng, CHANG Xiao-lin, XIAO Feng, et al. Study on early warning index of spatial deformation for high concrete dam[J]. Sci China Tech Sci,2011, 41(7): 992- 999. (in Chinese)) [17]华祖林,汪靓,顾莉,等. 基于门限极值理论的湖泊水质参照状态的确定[J]. 中国环境科学, 2014, 34(12): 3215- 3222. (HUA Zu-lin, WANG Liang, GU Li, et al. Estimation of the lake quality reference condition based on the threshold extreme theory[J]. China Environmental Science, 2014, 34(12): 3215- 3222. (in Chinese)) Real-time estimation and diagnosis of early warning indicator of slope displacement based on POT-catastrophe theory REN Jie1,2, SU Huai-zhi1,2, YANG Meng1,2, ZHOU Zhi-jie2 (1.StateKeyLaboratoryofHydrology-WaterResourcesandHydraulicEngineering,HohaiUniversity,Nanjing210098,China; 2.CollegeofWaterConservancyandHydropowerEngineering,HohaiUniversity,Nanjing210098,China) Abstract:Real-time estimation and diagnosis of slope early warning indicators are important means to monitor the safety state of slope and prevent the situation of the evolution from slope to landslide. Safety early warning pays more attention to extreme events, which are not common. The key to achieve safety early warning lies in whether we can accurately analyze the quantile of the slope effect quantity sequences and describe the tail characteristics of the slope effect quantity sequences. First of all, the slope displacement monitoring sequence can be divided by the interval of time; then, the thresholds of the slope displacement monitoring sequences at each time interval are drafted using Hill figure method; the part of the displacement monitoring sequence at each time interval that is supra-threshold is fitted by Generalized Pareto Distribution (GPD), and the tail characteristics of the part that is supra-threshold of displacement monitoring sequences are described progressively. So, the ability of the slope to resist historical loads is analyzed based on the model of peaks over threshold (POT) using extreme value theory. If the failure probability of the slope is provided, the real-time estimation sequences of early warming indicators of displacement can be obtained and the ability of the slope to resist extreme loads that may happen in the future can be exploited and evaluated. Finally, the real-time estimation sequences of early warming indicators of displacement are diagnosed by using cusp catastrophic model from catastrophe theory. Based on specific slope projects, the rationality of the mixed model of POT and catastrophe theory is verified and the modeling method of the mixed model will be a new way to achieve the real-time estimation and diagnosis of engineering early warning indicators. Key words:slope; early warning indicator of displacement; extreme value theory; POT model; cusp catastrophic theory 中图分类号:TV698.1 文献标志码:A 文章编号:1009-640X(2016)01-0030-07 作者简介:任杰(1992—),男,山西临汾人,硕士研究生,主要从事水工结构工程安全监控研究。 基金项目:国家自然科学基金资助项目(51179066,51409167,81279052,2014513311);国家重点实验室研究资助项目(20145028312); 江苏省杰出青年基金资助项目(BK2012036); 江苏省“333高层次人才培养工程”科研项目(2016-B1307101) 收稿日期:2015-04-17 DOI:10.16198/j.cnki.1009-640X. 2016.01.005 任杰, 苏怀智, 杨孟, 等. 边坡位移预警指标的实时估计与诊断[J]. 水利水运工程学报, 2016(1): 30-36. (REN Jie, SU Huai-zhi, YANG Meng, et al. Real-time estimation and diagnosis of early warning indicator of slope displacement based on POT-catastrophe theory[J]. Hydro-Science and Engineering, 2016(1): 30-36.) E-mail: 1538406080@qq.com