ENSO对珠江三角洲洪水影响
乔海艳,贾 琼,徐 阳
(河海大学港口海岸与近海工程学院,江苏南京 210098)
ENSO对珠江三角洲洪水影响
乔海艳,贾琼,徐阳
(河海大学港口海岸与近海工程学院,江苏南京210098)
摘要:根据珠江三角洲1951—2008年34个潮位站年极高水位资料和Nio 3.4区海洋尼诺指数资料,采用GEV分布进行洪水频率计算,分析不同重现期洪水位的变化情况,对比分析洪水位重现水平在1980年前后空间变化特征。采用滑动相关分析,探讨珠江三角洲近50年来洪水位对ENSO(El Nio/La Nia-Southern Oscillation)响应的年际变化特征。结果表明,珠江三角洲整个区域的洪水频率分布自下游到上游逐渐增大,沿海比中上游地区更易受洪涝灾害威胁。绝大多数站点不同重现期洪水位变化趋势一致,部分站点水位变化方向不完全一致。洪水位有减小趋势的站点分布在三角洲上游地区,中下游地区则主要呈现为增长趋势。洪水位与ENSO之间年际变化关系有明显阶段性,在1980年发生明显改变,跃变前后滑动相关系数的符号或强度有明显差异。洪水位对不同季节的ENSO响应不同,不同时期ENSO对洪水位的影响不同。
关键词:ENSO事件; 洪水重现期; 年代际变化; 珠江三角洲
厄尔尼诺—南方涛动(ENSO)是全球海气耦合的结果,是热带太平洋地区海气系统年代际气候变化的最强信号。研究表明,许多地区的气温和降水等气象要素的异常变化都与ENSO事件有较密切联系[1-2],El Nio年全球陆地平均年降水量减少,La Nia年降水量增加[3]。ENSO事件不仅是造成全球气候异常的一个重要原因,也是导致亚洲季风异常和我国旱涝发生的关键因素,带来严重的气候灾害和重大经济损失。ENSO通过影响东亚夏季风进而影响我国降水,暖事件(冷事件)对东亚夏季风有减弱(增强)作用[4],El Nio年夏季北方的干旱趋势明显,秋、冬季江南多雨,北方少雨,La Nia年则相反[3]。根据美国国家海洋和大气管理局(NOAA)提供的数据,1951—2008年共发生了18次暖事件,14次冷事件。
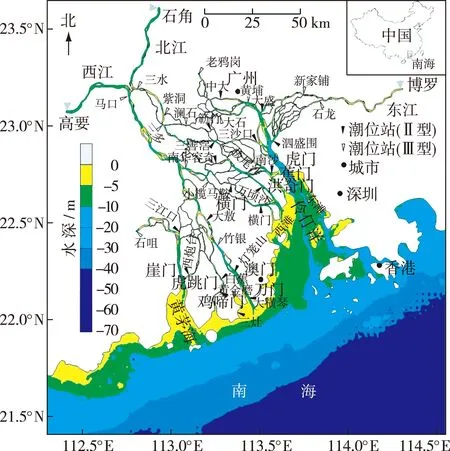
图1 珠江三角洲潮位站点分布Fig.1 Location of gauging stations at Pearl River delta
珠江三角洲由西江、北江、东江等河流堆积形成,河网密布,其密度为0.68~1.07 km/km2,河口地貌复杂,大小河流纵横交错,相互贯通[5]。由于人类活动和气候变化等多重因子的叠加影响,近几十年,特别是20世纪90年代以来,珠江三角洲流域水文及河流地貌特征发生了巨大变异,导致区域极端水位的重现期变化。洪水灾害呈逐渐加重趋势,1990年后相继发生了“94.6”,“98.6”,“05.6”,“08.6”洪水,使珠江三角洲地区的经济发展与洪涝灾害风险的矛盾愈加尖锐[6-7]。珠江三角洲河网区洪水位总体呈上升趋势,年极值水位在1980年左右发生突变,主要原因是河网区人类采沙活动自20世纪80年代以来自口门向河网区及上游推进[6]。珠江三角洲河网区洪水位的长期变化趋势,反映了河床演变的一系列特性,可以在一定程度上反映出河网区河道的冲淤变化趋势在不同时期的调整。
1资料和分析方法
本文所用资料包括1951—2008年珠江三角洲34个潮位站的实测年极高水位资料和Nio 3.4区海洋尼诺指数(ONI)资料。
通常对水文要素极值的频率分析主要有两种方法:一是通过某种统计分布函数对水文要素值进行拟合,分析极端事件的累积频率及相应重现水平;二是利用极值分布理论进行拟合分析。20世纪30年代,R. A. Fisher等[8]证明极值具有渐进分布特性,概括了3类极值分布模型,分别为极值I型(Gumbel)、极值Ⅱ型(Fréchet)及极值III型(Weibull)分布。A. F. Jenkinson[9]根据极值分布理论,将3种类型的经典极值分布发展为一种统一的具有3参数的极值分布函数——广义极值分布(GEV)。GEV方法适用性更强,在水文和洪水频率分析[10]等领域得到了广泛应用,能避免以往单独采用某一种分布的不足,在理论上是合理的,计算结果比传统方法更可靠。
GEV模型的I,II和III型分布,分别对应于形状参数ξ=0,ξ<0和ξ>0。根据美国联邦应急管理署(FEMA)的指导意见和 W. J. Visseman等[11]的介绍,其概率密度函数(PDF)为:
(1)
2005年,FEMA建议采用最大似然[12]参数估计的GEV分布进行极值分析。用于GEV模型的极大似然参数方法可表示为:
(2)
通过对珠江三角洲34个潮位站年极高水位时间序列进行基于极大似然参数估计的GEV模型,得到各个站点所属类型如图1所示。采用Kolmogorov-Smirnov拟合检验方法[12],对结果进行拟合优度检验,结果表明在0.05显著性水平,所有站点的拟合结果被接受。
尽管珠江三角洲河网区水位总体呈上升趋势,但由于河网区人类采沙活动从20世纪80年代以来自口门向河网区及上游推进,年极值水位在1980年左右发生了突变[6]。水位变化影响河床演变,而河床变化又反过来影响河网区的水位变化。本文将1951—2008年的极高水位分为1980年前后两个样本,并对其进行洪水频率分析,比较1980年前后不同重现期对应洪水位的时空变化特征。
ENSO具有季节锁相性,发生发展于春夏季、秋冬季达到鼎盛、次年夏季衰亡。研究表明,ENSO对气候异常的影响与其所处阶段关系密切[13]。本文利用年极高水位资料与Nio 3.4区冬季12月至翌年2月(DJF)的ONI指数计算二者的滑动相关系数,以表征处于鼎盛阶段的ENSO对洪水位的影响,利用年极高水位与夏季6—8月(JJA)的ONI指数之间的相关关系来表征处于衰减阶段的ENSO对洪水位影响。由此揭示珠江三角洲洪水位与处于不同阶段ENSO关系的年代际变化特征。
为了揭示珠江三角洲不同阶段ENSO与洪水位关系的年代际变化特征,取滑动窗口n=11年进行滑动相关分析[14],所得的滑动相关值在第6年进行标注,利用Pearson’s相关,得到相应的11年滑动相关系数随时间变化的曲线。
2不同重现期洪水位的时空变化特征
在整个时间样本内,珠江三角洲不同重现期洪水位自下游到上游逐渐增大,沿海地区比中上游等其他地区更易受洪涝灾害威胁,是发生洪水的敏感区和脆弱区。同为50年一遇洪水,珠江上游水位均超过5 m,三水站洪水位甚至达10.14 m(见表1),中游50年一遇洪水位多为3~7 m,而下游这一级别的洪水位基本不超过3 m。三角洲上游区域的50年一遇洪水水位与10年一遇洪水位差值超过0.5 m,下游区域50年一遇与10年一遇洪水位的差值略大于0.25 m。
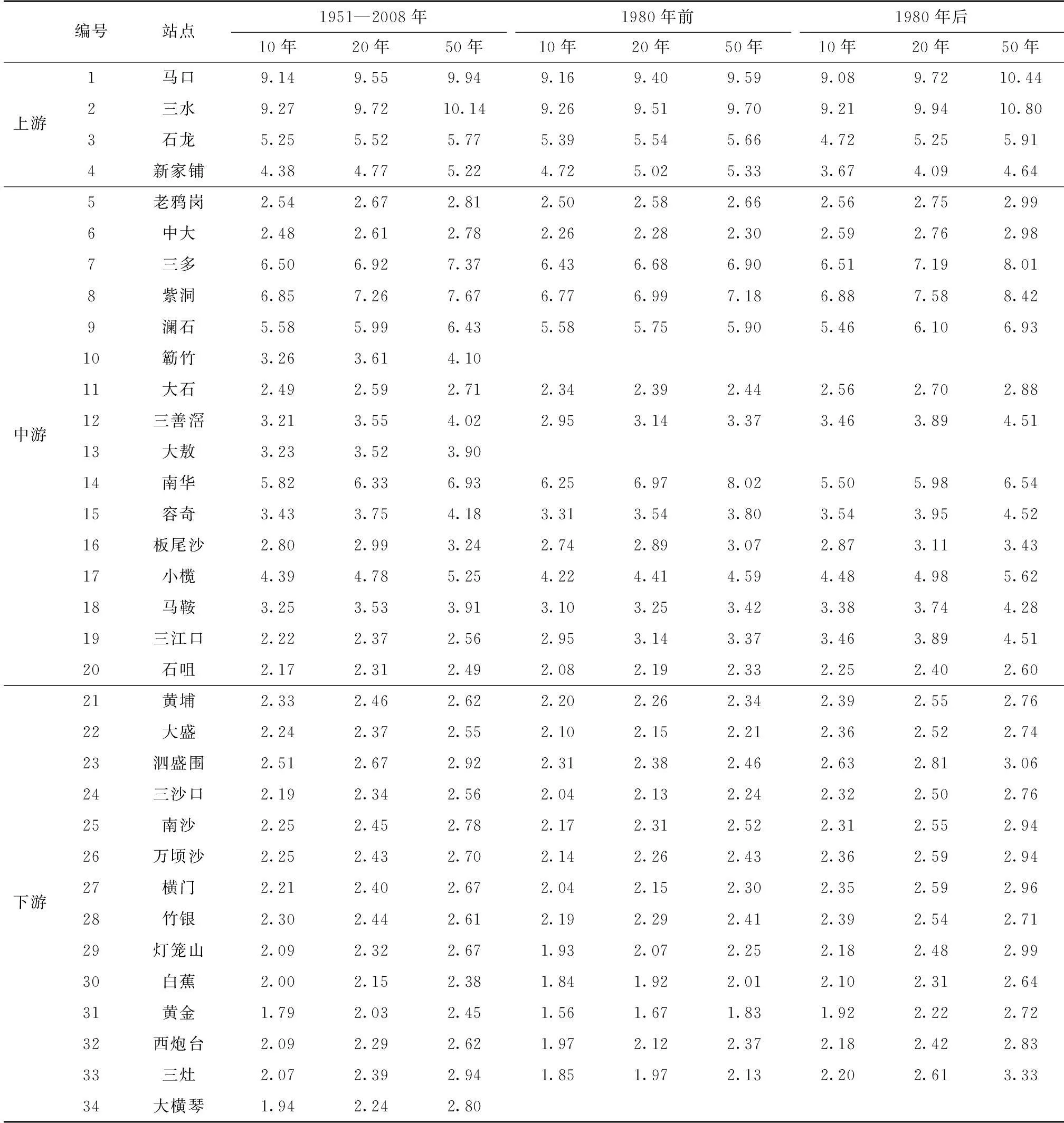
表1 珠江三角洲不同重现期对应洪水位
在南华站,50年一遇洪水位比10年一遇的高1.11 m(表1),这一差值在34个站点中最大。1980年前后31个站点(不包括大敖、大横琴、簕竹3站,因其观测数据较少)重现期为10年、20年和50年的水位有明显差别。尽管三角洲在1980年前后水位发生了巨大变化,但仍遵守不同重现期洪水位自下游至上游逐渐增大的规律。
计算结果还表明,珠江三角洲1980年前后洪水位有着复杂的时空变化特征。绝大多数水文站点不同重现期对应的洪水位变化趋势一致,即1980年后的洪水位有明显抬升,部分水文站点水位变化方向不完全一致。其中26个水文站点(占所选站点的81.25%)的洪水位呈增长趋势,下游三灶、灯笼山、黄金的洪水位抬升量甚至超过了中游部分站点。澜石、马口和三水20年一遇洪水位和50年一遇洪水位变化趋势为正,而10年一遇洪水位变化趋势为负。石龙50年一遇洪水位变化趋势为正,而10年及20年一遇洪水位变化趋势为负。南华及新家铺洪水位呈明显下降趋势,其中南华站的水位下降了0.75~1.50 m,新家铺的水位下降了0.7~1.05 m。洪水位有减小趋势的站点分布在三角洲上游地区,中下游地区的洪水位主要呈增长趋势。
由水文统计分析,在珠江三角洲上游,马口和三水各时期重现期变化均不太明显,石龙和新家铺在20世纪80年代后洪水位明显抬升。三角洲中部地区站点分布密而广,变化情况较为复杂,但总体上各时段洪水位都呈现抬升趋势。整个口门区各站洪水位变化情况相似,每个站点的洪水位都有抬升,尤以西四口门为甚。
3洪水位对ENSO响应的年代际变化
珠江三角洲上游地区,如图2(a)所示的冬季ENSO与洪水位的关系表明,整体上正相关与负相关交替出现,且以正相关为主,阶段性明显,20世纪70—80年代相关性很低。图2(b)表明,1980年代之前,夏季ENSO与洪水位呈负相关,20世纪90年代至21世纪00年代相关性发生跃变,正负交替,但相关性一直维持在低水平,这意味跃变年前后该区洪水位与Nio 3.4区ONI年际变化关系差异较为明显。

图2 珠江三角洲极高水位与ENSO的11年滑动相关系数Fig.2 11-year sliding correlation coefficients between AMWL and ENSO in Pearl River delta
由图2(c)可知,中游地区在20世纪70年代前,洪水位与冬季ENSO的关系交替出现正负相关,且相关性低,70—80年代,一直维持稳定的负相关。在80年代相关性发生了显著的年代际变化,负相关系数迅速增大为正相关,并且在90年代初期再次发生转变。中游地区洪水位与夏季ENSO呈明显负相关(图2(d)),并且相关系数在80年代有一个较为明显的突变。
如图2(e),下游地区冬季ENSO与洪水位的关系与中上游一样,在20世纪80年代有一个较大突变,所不同的是其长期较为稳定的明显负相关经过短暂的正相关后,再次变为明显的负相关。但这种关系随着年代的推移发生了改变,下游地区的负相关性逐渐减小,并转变为正相关。夏季ENSO与洪水位的相关关系(图2(f))长期较弱,70年代前期至90年代为负相关,其他年代际基本维持正相关。
4结语
本文根据1951—2008年珠江三角洲34个潮位站年极高水位和Nio 3.4区ONI指数,采用GEV分布对各站点的年最高洪水位时间序列进行洪水频率计算,比较1980年前后洪水位的时空变化。采用滑动相关分析,探讨近50年来珠江三角洲洪水位对ENSO事件响应的年代际变化特征,得到下面一些主要结论:
(1)整个珠江三角洲的不同重现期洪水位自下游到上游逐渐增大,沿海地区比上中游等其他地区面临更大的洪涝灾害威胁。绝大多数水文站点不同重现期对应的洪水位变化趋势一致,部分水文站点水位变化方向不完全一致。洪水位有减小趋势的站点分布在三角洲上游地区,中下游地区水文站点的洪水位主要呈增长趋势。
(2)上游西、北江的马口和三水两站在各个时期重现期变化均不太明显,东江的石龙和新家铺在20世纪80年代后洪水位有明显抬升。三角洲中部地区水文站点在各个年代洪水位都呈现出抬升趋势。整个口门区各个站点洪水位变化情况相似,每个站点的洪水位都有抬升,西四口门洪水位抬升最为明显。
(3)珠江三角洲上游、中游及下游洪水位与ENSO的关系随时间的变化都具有明显的年代际特征。近50多年来,根据滑动相关系数的变化,在1980年代发生了较为显著的跃变。跃变前后ENSO与珠江三角洲洪水位之间的分段相关关系具有明显差异。
(4)洪水位对冬季ENSO的响应与其对夏季ENSO的响应有明显差异。洪水位受冬季ENSO影响要明显大于夏季ENSO,并且其波动更大,同样是El Nio或La Nia 事件,在不同年代背景下其对珠江三角洲洪水位的影响也具有不同的表现。
参考文献:
[1]SHIAU J T. Return period of bivariate distributed hydrological events[J]. Stochastic Environmental Research and Risk Assessment, 2003, 17(1-2): 42- 57.
[2]KLAUS W, MICHAEL S T. El Nio/Southern Oscillation behaviour since 1871 as diagnosed in an extended multivariate ENSO index (MEI.ext)[J]. International Journal of Climatology, 2011, 34: 1074- 1087.
[3]龚道溢, 王绍武. 近百年ENSO对全球陆地及中国降水的影响[J]. 科学通报, 1999, 44(3): 315- 320. (GONG Dao-yi, WANG Shao-wu. ENSO impacts on the global land and China precipitation in the past century[J]. Chinese Science Bulletin, 1999, 44(3): 315- 320. (in Chinese))
[4]臧增亮, 包军, 赵建宇, 等. ENSO对东亚夏季风和我国夏季降水的影响研究进展[J]. 解放军理工大学学报:自然科学版, 2005, 6(4): 394- 398. (ZANG Zeng-liang, BAO Jun, ZHAO Jian-yu, et al. Recent progresses of studies on influence of ENSO on the East Asian summer monsoon and China summer rainfall[J]. Journal of PLA University of Science and Technology, 2005, 6(4): 394- 398. (in Chinese))
[5]时翠, 陈晓宏, 张强. 近几十年来珠江三角洲1月和7月水位变异分析[J]. 热带地理, 2012, 32(3): 233- 240. (SHI Cui, CHEN Xiao-hong, ZHANG Qiang. Change-points of water levels in the Pearl River Delta in January and July for the last decades[J]. Tropical Geography, 2012, 32(3): 233- 240. (in Chinese))
[6]ZHANG W, YAN Y X, ZHENG J H, et al. Temporal and spatial variability of annual extreme water level in the Pearl River Delta, China[J]. Global and Planetary Change, 2009, 6(9): 35- 47.
[7]蒋陈娟, 杨清书, 戴志军, 等. 近几十年来珠江三角洲网河水位时空变化及原因初探[J]. 海洋学报, 2012, 34(1): 46- 56. (JIANG Chen-juan, YANG Qing-shu, DAI Zhi-jun, et al. Spatial and temporal characteristics of water level change and its causes in the Zhujiang Delta in recent decades[J]. Acta Oceanologica Sinica, 2012, 34(1): 46- 56. (in Chinese))
[8]FISHER R A, TIPPETT L H. Limiting forms of the frequency distribution of the largest or smallest member of a sample[J]. Proc Cambridge Philos Soc, 1928, 24: 180- 190.
[9]JENKINSON A F. The frequency distribution of the annual maximum (or minimum) values of meteorological elements[J]. Quarterly Journal of the Royal Meteorological Society, 1955, 81: 158- 171.
[10]XU S D, HUANG W R. Estimating extreme water levels with long-term data by GEV distribution at Wusong station near Shanghai city in Yangtze Estuary[J]. Ocean Engineering, 2011, 38(2- 3): 468- 478.
[11]VIESSMAN W J, LEWIS G L. Introduction to hydrology[M]. New York: Harper Collins College Publishers, 1996.
[12]陈子燊, 刘曾美, 路剑飞. 广义极值分布参数估计方法的对比分析[J]. 中山大学学报:自然科学版, 2010, 49(6): 105- 109. (CHEN Zi-shen, LIU Zeng-mei, LU Jian-fei. Comparative analysis of parameter estimation methods of generalized extreme value distribution[J]. Acta Scientiarum Naturalium Universitis Sunyatseni (Natural Sciences), 2010, 49(6): 105- 109. (in Chinese))
[13]倪东鸿, 孙照渤, 赵玉春. ENSO循环在夏季的不同位相对东亚夏季风的影响[J]. 南京气象学院学报, 2000, 23(1): 48- 54. (NI Dong-hong, SUN Zhao-bo, ZHAO Yu-chun. Influence of ENSO cycle at different phases in summer on the east Asian summer monsoon[J]. Journal of Nanjing Institute of Meteorology, 2000, 23(1): 48- 54. (in Chinese))
[14]TIMO A, RASANEN M K. Spatiotemporal influences of ENSO on precipitation and flood pulse in the Mekong River basin[J]. Journal of Hydrology, 2013, 476: 154- 168.
Impacts of ENSO on different flood frequencies in Pearl River delta
QIAO Hai-yan, JIA Qiong, XU Yang
(CollegeofHarbor,CoastalandOffshoreEngineering,HohaiUniversity,Nanjing210098,China)
Abstract:Based on annual maximum water level (AMWL) data obtained from 34 gauging stations in the Pearl River delta (PRD) and the oceanic Nino index (ONI) data in the Nio 3.4 region from 1951 to 2008, the GEV distribution model is used to get the flood frequency analysis of AMWL. In order to comprehensively understand the water level fluctuations characteristics in the delta, the water level variation corresponding to different flood frequencies calculated from a series of pre-1980 and post-1980 years are examined. The studies of interdecadal variations in the response of the flood water level to ENSO in the past fifty years have been carried out by using moving correlation. The space-time variations in the flood water levels corresponding to different return periods in the PRD region suggest that the flood water level increases gradually from the coastal areas to the riverine system. The flood-frequency variations have shown that the most serious flood-risk is in the coastal region because this region is extremely vulnerable to the flood hazards. The flood water level increments corresponding to different increments of the flood periods in all 34 sites are great. In the upper PRD, the flood water levels show a decreasing trend while there is an increasing trend in the middle and lower PRD. The long-term variation of interannual relationships between ENSO and the flood water level has a significant stage characteristic and has a great change in the 1980s. Before and after the abrupt change, the correlation coefficients have remarkable differences. The flood water levels have various responses to various seasonal ENSO events.
Key words:ENSO event; return period of flood; interdecadal variation; the Pearl River delta
中图分类号:P331.1
文献标志码:A
文章编号:1009-640X(2016)01-0122-06
作者简介:乔海艳(1990—),女,江苏连云港人,硕士研究生,主要从事港口、海岸及近海工程研究。E-mail:pghaiyan@163.com
收稿日期:2015-05-29
DOI:10.16198/j.cnki.1009-640X.2016.01.018
乔海艳, 贾琼, 徐阳. ENSO对珠江三角洲洪水影响[J]. 水利水运工程学报, 2016(1): 122-127. (QIAO Hai-yan, JIA Qiong, XU Yang. Impacts of ENSO on different flood frequencies in Pearl River delta[J]. Hydro-Science and Engineering, 2016(1): 122-127.)

