基于截尾分位数回归模型的上市公司财务困境影响因素研究
蒋翠侠, 赵 怡, 许启发
(合肥工业大学 a.管理学院; b.过程优化与智能决策教育部重点实验室,合肥 230009)
基于截尾分位数回归模型的上市公司财务困境影响因素研究
蒋翠侠a,b,赵怡a,许启发a,b
(合肥工业大学 a.管理学院; b.过程优化与智能决策教育部重点实验室,合肥230009)
摘要:用生存分析方法研究财务困境,通常用Cox比例风险模型来建模,但Cox比例风险模型的应用需要满足两个假定,现实中难以同时满足。为解决Cox比例风险模型的不足,将截尾分位数回归模型应用到生存分析中。该模型对生存时间直接进行建模,增加了模型的可解释性,为分析生存数据提供了一种有效的方法,并可借此对上市公司发生财务困境的影响因素做出判断。实证结果表明,在上市公司财务困境研究中,将截尾分位数回归模型和Cox比例风险模型的实证结果相比较,发现截尾分位数回归模型的结果更为准确。
关键词:财务困境;生存分析;截尾分位数回归;ST公司
一、引言
在市场经济中,上市公司首次上市后是否会陷入财务困境是金融、会计研究领域中的一个值得探讨的问题。选择合理的财务风险分析方法,采取正确的财务战略措施,有效地防范和控制财务风险,从而预防陷入财务困境,对我国上市公司健康、持续的发展有着极其重要的现实意义。
国外很早就有学者开始对财务困境进行研究。Willim(1966)[1]认为,应该以预测财务危机为目标,其利用单变量判别模型分析了所选取财务指标的预测效率。Altman(1968)[2]利用多变量判别模型来预测上市公司的破产可能性。Ohlson(1980)[3]最早利用Probit方法来预测财务困境。Lane等(1986)[4]最早将Cox比例风险模型应用在预测银行倒闭的问题上,发现Cox比例风险模型均优于传统的判别分析方法。
国内学者研究财务困境影响因素的时间较晚。陈静(1999)[5]利用同行业、同规模非ST公司和ST公司各27家,选取其中4个财务指标进行研究分析。卢声等(2001)[6]选取基本的财务指标作为解释变量来建立预测模型,运用Fisher判别分析方法,估计出各个财务指标变量的系数。谢赤、罗长青(2007)[7]根据各种财务困境预测模型对分布的要求,将所有的模型方法分为参数法和非参数法(含生存分析),并指出在这种分析方法中无需规定基础风险函数的具体分布,更符合企业财务困境的真实情况。邓晓岚、陈晓辉、王宗军(2007)[8]运用非参数生存分析方法,对中国上市公司的财务困境风险进行了评价,认为综合类上市企业的多元化经营可能有助于分散风险。陈磊、任若恩(2007)[9]运用Cox比例风险模型研究上市公司出现财务困境的问题,以133个制造业上市公司作为研究样本,发现盈利能力、现金能力、资产周转率与财务风险负相关,而期间费用与财务风险正相关。
目前国内对公司财务困境的研究主要使用Cox比例风险模型,Cox比例风险模型虽然有很多优点,但是其模型不允许协变量影响的符号随着响应的大小而改变,并且是对生存危险率建模。为了改变这种情况,可以尝试其他建模方法。由Powell[12]提出的截尾分位数回归模型就为这样的问题提供了一个相当自然和直接的方法。本文试图在以下两个方面进行探索研究:一是在样本选取方面,并没有按照大多数文献采用的“配对抽样”的方法进行样本选取,即首先选取一定数量的财务困境公司,然后再按照一定标准(行业相同且规模相近)选取相对应的非财务困境公司,作为配对样本。而是直接选取样本,不人为调整ST公司与非ST公司的比例;二是国内目前尚未有将截尾分位数回归模型应用到财务困境中的文献,本文将截尾分位数回归模型和Cox比例风险模型的实证结果相比较,对上市公司财务困境影响因素做出判断。
二、财务困境的含义与计量
财务困境是财务风险的一种极端表现,是指企业无法偿还到期债务所引发的危机,通常从财务正常渐渐发展到财务困境,不存在一个明确的分界点将企业分为陷入财务困境和没有陷入财务困境两类。由于国内财务困境预测的研究对象主要针对上市公司,故一般将财务困境界定为财务状况异常而被“特别处理”。
1.生存时间的界定
考虑到上市公司发生财务危机、陷入财务困境是一个动态持续的过程,因此本文给定的上市公司生存时间是从公司正常持续经营的状态到陷入财务困境的时间。即将公司上市时间确定为生存时间的观测起点。
对于陷入财务困境的样本公司,观测终点则是上市公司首次被进行特别处理的时间;对于非财务困境的样本公司,观测期的终点设置为2014年12月31日。
2.财务指标的确定
建立财务困境预测模型关键在于识别出其核心影响因素。在初次选取财务指标时,原则上尽可能地全面揭示企业财务和综合发展水平,构建能够全面反映公司的财务状况,参照国内外学者的实证结果,选用最易获取的财务比率指标作为预测指标,从企业的偿债能力、营运能力、盈利能力、现金流量、风险水平、发展能力、股东获利能力、相对价值指标、股利分配九个方面33个指标作为财务困境影响因素,为了方便运算,将影响因素名称更换为Xi(i=1,2,…,33)的形式,具体内容见下页表1。

表1 财务困境影响因素
三、模型与方法
1.模型表示

(1)
其中β(τ)是回归系数向量,误差项εi(i=1,…,n)为独立的随机变量。
2.模型估计
回归系数向量β(τ)可以通过式(2)来估计:
(2)
在很多实际应用中,所有观测值的删失时间都能被观测到是不现实的。通常情况下,只能观测到随机变量Yi=min{Ti,Ci}和指示变量δi=1。当δi=1时,观测到的Yi是准确的生存时间,Ci观测不到,这时需要新的方法。
Portnoy[13]提出了一个方法,该方法就是将每个截尾观测的潜在贡献值重新分配到它右侧的观测中,即将每个截尾观测的截尾概率值P{Yi>Ci}重新分配到它右侧的观测中。通过这种算法可以得到生存函数的估计值。因为分位数函数只与位置有关,取决于残差的符号,所以Ci点处的贡献值可能被重新分配到大于所有数据的任何一点处,不是必须局限地分配到大于Ci的某些特定观测对象上,我们就可以将加权的思想运用到截尾分位数回归中。
当观测对象发生截尾时,对应的截尾生存时间和潜在真实的生存时间分别为Ci和Ti,满足Ci
(3)

(4)
3.模型优点
截尾分位数回归模型和Cox比例风险模型相比,优势在于它不但可以描述因变量均值与自变量的关系,还可以度量分布的低尾和高尾对自变量的影响。不同分位数下回归系数及其统计的显著性都存在巨大差异,这样可以获取分布函数的形状和参数信息,得到的结果也会更加真实可信。
四、数值模拟
本节通过数值模拟,对比截尾分位数回归模型和Cox比例风险回归模型。
1.满足比例风险假定的模拟分析

(2)结果比较对模拟数据进行建模,结果见表 2。结果显示,对于满足比例风险假定的数据,Cox比例风险模型和截尾分位数回归模型的回归系数与真实值1非常接近,但截尾分位数回归模型的回归系数更加准确。由于模拟数据中不存在异质问题,所以不同分位数水平对应的回归系数非常接近,随着截尾比例的增加,回归系数可能会逐渐偏离真实值。

表2 不同截尾比例下回归系数的模拟分析
注:随着截尾比例的增加,无法估计高分位点对应结果,这里以NA来表示。
2.违背比例风险假定的模拟分析
由于对数正态回归模型不满足Cox比例风险假定,故此次模拟采用对数正态回归模型产生数据。
(1)数据选取确定样本量为200,截尾比例分别为20%、40%、60%。首先,产生服从(0,1)均匀分布的随机数作为自变量x,再产生服从N(0,1)正态分布的随机数作为误差项ε,产生服从B(200,0.2)的随机数作为截尾指示变量,这时截尾比例为20%。令β=1,利用t=exp(1+βx+ε)得到相应的生存时间t。每次得到1 000个样本,分别采用Cox比例风险模型和截尾分位数回归模型,计算出这1 000个样本的回归系数的均值以及与真实值的误差。
(2)结果比较对模拟数据进行建模,结果见表3。结果显示,对于不满足比例风险假定的数据,Cox比例风险模型的回归系数有偏;截尾分位数回归模型的回归系数与真实值1非常接近,随着截尾比例的增加,回归系数可能会逐渐偏离真实值。

表3 不同截尾比例下回归系数的模拟分析

续表
注:随着截尾比例的增加,无法估计高分位点对应结果,这里以NA来表示。
五、实证分析
1.数据选取
本文选取我国2000年上市的142家公司作为研究对象,将公司上市时间确定为生存时间的观测起点,这样对于上市公司而言界定生存时间的起点方面,可以获取所有上市公司在生存时间起点的信息,从而能够有效地避免可能会干扰模型的左删失数据。观测期终点以样本是否触发特定的事件来分别确定。对于陷入财务困境的样本公司,观测终点则是上市公司首次被进行特别处理的时间;对于非财务困境的样本公司,观测期的终点设置为2014年12月31日。在这期间首次被特别处理的公司的生存时间为上市时间与被处理时间之间的月数,且指示变量为1。未被处理的公司的生存时间为从上市时间与观测期终点时间结束时间之间的月数,且指示变量为0。根据前文表1所选出的财务指标,我们通过国泰安数据库搜集了相关公司的财务指标数据,并与其生存时间以及生存状态共同组成了上市公司生存分析的数据。
2.财务困境影响因素实证结果
本节拟合Cox比例风险模型与截尾分位数回归模型,对上市公司财务困境开展定量研究,并将研究结果进行对比。
(1)Cox比例风险模型结果第一,利用全部变量拟合Cox比例风险模型。根据Cox比例风险模型对上市公司生存分析数据进行分析,其估计结果见表 4。由该表可以看出,利用全部解释变量拟合Cox等比例风险模型的拟合效果并不好,只有X3一个指标是显著的,考虑到变量之间的多重共线性以及无关变量的存在,下面利用AIC准则来选取变量。
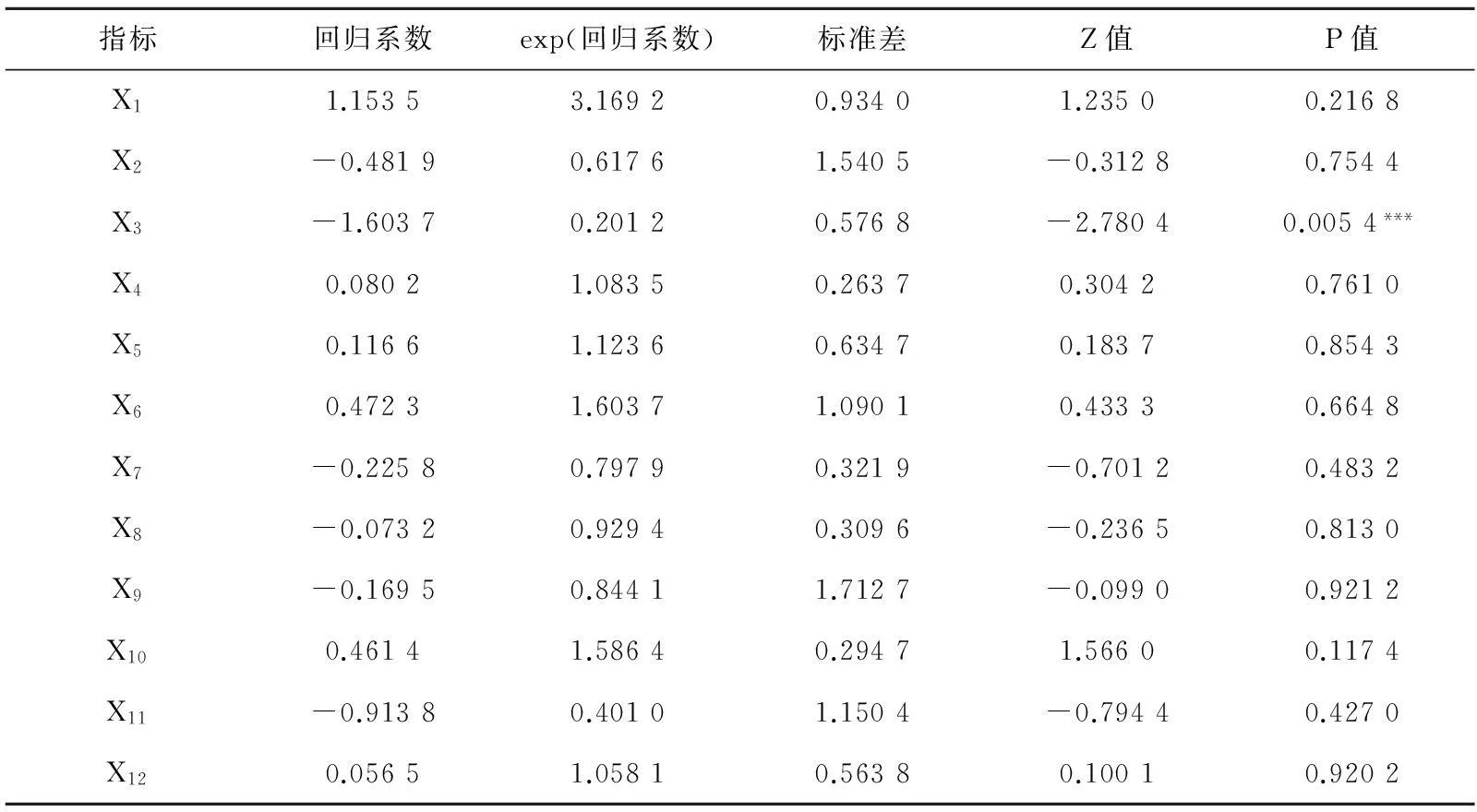
表4 拟合Cox等比例风险模型回归系数估计
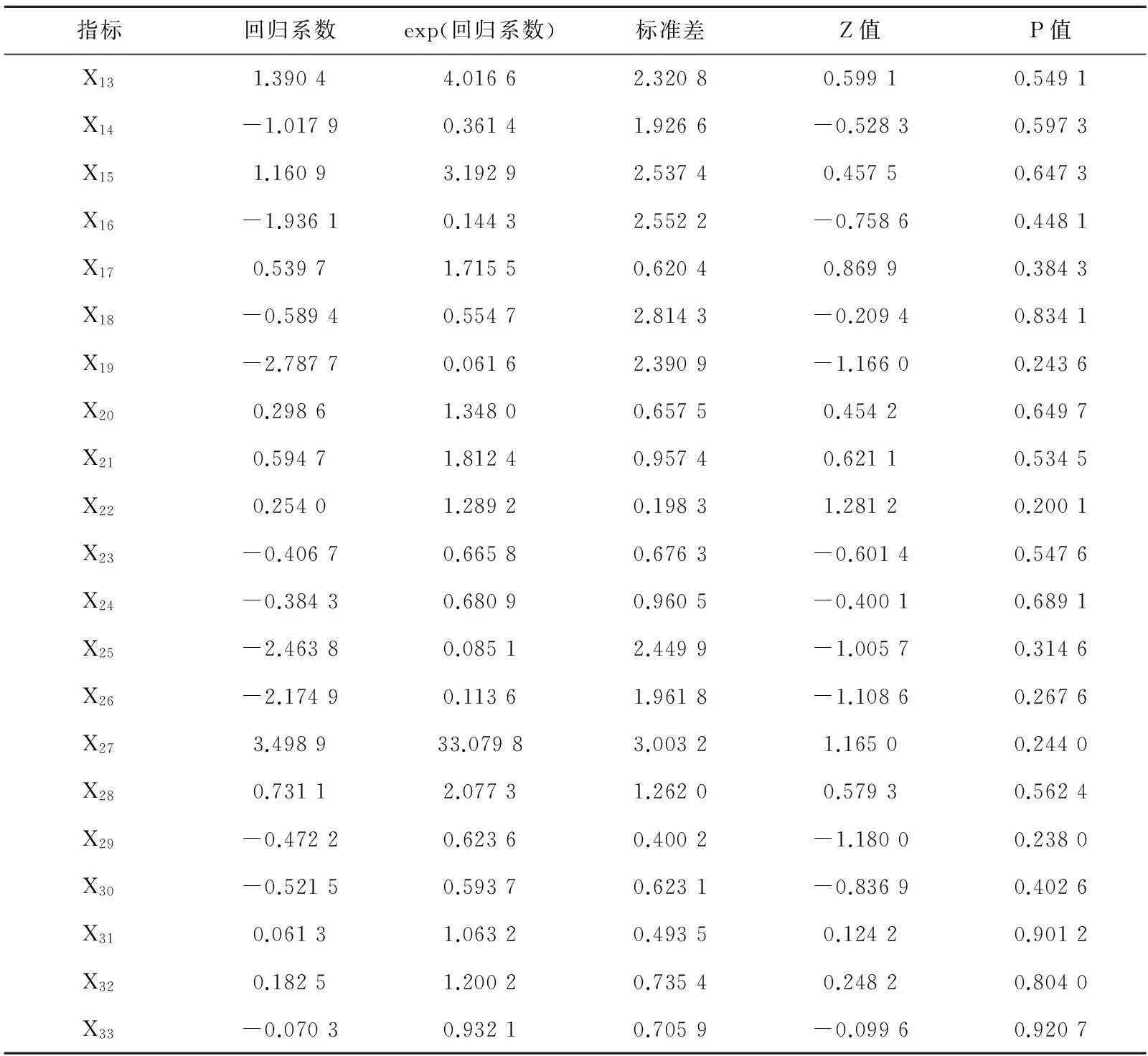
续表
注:***表示1%水平下显著。
第二,根据AIC准则选择最优Cox模型为优化Cox比例风险模型的结果,使用AIC准则进行变量选择,并对变量选择后的模型进行参数估计,结果见表5。

表5 根据AIC准则选择最优Cox模型系数估计
注:***、**与*分别表示1%、5%与10%水平下显著。
从表 5可以看出,通过AIC准则,选出X1、X3、X16、X28、X29这些显著的变量,其中X1、X3在α为1%的水平下显著,X16在α为5%的水平下显著,X28、X29在α为10%的水平下显著,而所估计的结果与最初估计的结果相比,模型估计的结果更好。这表明除去多重共线性后,X1流动比率、X3现金比率、X16总资产净利润率、X28可持续增长率、X29每股收益这些指标对于预测上市公司是否陷入财务困境是有效的。从入选的指标来看,反映公司偿债能力的指标最多,说明上市公司的财务风险状况与其偿债能力的联系最为紧密。另外反映公司盈利能力、发展能力和股东获利能力的指标也有涉及。
从单个变量的系数符号来看,X3现金比率的系数为负,与财务困境风险负相关,由于现金比率与流动负债成反比,说明公司的流动负债越多,财务困境风险就越大。X16总资产净利润率系数为负,说明公司的盈利能力越强越不容易陷入财务困境。X29每股收益系数为正,说明每股收益越高越不容易陷入财务风险。X1流动比率的系数为正,这可能由于流动比率是对偿债能力的粗略估计,不同行业的流动比率,通常有明显的差别。所以这可能是导致与我们通常认为的结果不一致的原因。X28可持续增长率的系数也为正,表明与财务风险正相关,这点和我们通常认为的并不相同,具体的原因还有进一步探究。
(2) 截尾分位数回归模型结果根据AIC准则选取的变量,用截尾分位数回归模型对上市公司生存分析数据进行分析。参数估计如表 6和下页图1所示。

表6 截尾分位数回归系数估计

续表

图1 拟合截尾分位数回归模型系数随τ的变化情况
表6和图1给出了拟合截尾分位数回归的结果,图1中间的实线表示在不同分位数下各个参数的回归系数,阴影区域为95%置信区间带。
从图1可以看出,随着分位点的增加,速动比率X2对企业生存时间的影响增大。 速动比率代表企业以速动资产偿还流动负债的综合能力。由于存货没有变现能力,所以速动比率比流动比率更能表现一个企业的短期偿债能力。现金比率X3的系数在整个分位点为正,说明其与企业生存时间正相关,并且系数随着分位点的增加先上升后下降,说明现金比率并非是越高越好,而是保持在一定范围内最好,一般认为现金比率保持在20%以上为好,但这一比率过高,意味着企业流动资产未能得到合理运用,现金类资产获利能力低,会导致企业机会成本增加。 净资产收益率X18的系数在整个分位点为正,说明其与企业生存时间正相关,并且随着分位点的增加,净资产率对企业生存时间的影响增大。 综合杠杆X27系数在低分位点为正,随着分位点的增加逐渐下降至负数,说明综合杠杆较低时,对企业生存时间的影响是正向的,随着综合杠杆的增加,企业所面临的风险也就越大,对生存时间的影响逐渐变为负向影响。而可持续增长率X28的系数随着分位点的增加先下降后增加,说明可持续增长率对生存时间的影响先增大后减小。 每股收益X29的系数在低分位点为正,随着分位点的增加逐渐下降为负数,说明在低分点下,每股收益对企业生存时间的影响是正向影响,但是却随着分位点的增加而下降,说明每股收益越高反而越容易发生财务困境,这可能是因为每股收益过高有可能是因为每股的股价较低,并不能完全反映上市公司的财务状况。
整体上看,Cox比例风险模型和截尾分位数回归模型的结果基本一致,但是截尾分位数回归模型能够反映系数随τ的变化情况,更符合实际情况。
六、结论与启示
将截尾分位数回归模型引入生存分析,对生存时间直接进行建模,增加了模型的可解释性,并且能够对上市公司财务困境的影响因素做出准确的判断。本文通过数值模拟,区分两种状态,对比了截尾分位数回归模型与Cox比例风险模型的效果,发现前者优于后者。最后,选取我国上市公司作为研究对象,对上市公司陷入财务困境的影响因素进行了实证研究。
实证结果表明:第一,截尾分位数回归模型能够从众多财务指标中筛选出主要影响因素,即偿债能力、盈利能力、发展能力以及股东获利能力等,有利于揭示上市公司陷入财务困境的机理,从而便于提出有针对性的风险控制措施;第二,截尾分位数回归模型能够反映系数随τ的变化情况,可以更加准确地反映财务指标对企业生存时间的影响。因此,在分析企业财务困境时,可以将截尾分位数回归模型的结果与Cox比例风险模型结果进行对比,以便考察在不同的市场环境下(与分位数点相对应)上市公司财务困境的影响因素,对其进行准确的识别。
参考文献:
[1]Beaver W H. Financial ratios as predictors of failure[J]. Supplement to Journal of Accounting Research, 1966,(4):71-111.
[2]Altman E I. Financial ratios, discriminant analysis and the prediction of corporate bankruptcy[J]. The Journal of Finance, 1968,(4): 589-609.
[3]Ohlson J A. Financial ratios and the probabilistic prediction of bankruptcy[J]. Accounting Research, 1980,(1): 109-131.
[4]Lane W R, Looney W, Wansley J W. An application of the Cox proportional hazareds model to bank failure[J]. Journal of Banking and Finance, 1986,(4): 511-531.
[5]陈静. 上市公司财务恶化预测的实证分析[J]. 会计研究, 1999,(4): 45-49.
[6]卢声, 任若恩, 李清. 中国上市公司财务危机困境模型的研究[J]. 北京航空航天大学学报, 2001,(1): 22-27.
[7]谢赤, 罗长青. 财务困境的参数方法与非参数方法及其比较[J]. 当代财经, 2007,(7):113-117.
[8]邓晓岚, 陈朝晖, 王宗军. 公司财务困境非参数生存分析模型评价[J]. 武汉理工大学学报, 2007,(6): 121-124.
[9]陈磊, 任若恩. 基于比例危险和主成分模型的公司财务困境预测[J]. 财经问题研究, 2007,(7): 93-96.
[10]彭非,王伟. 生存分析[M]. 北京: 中国人民大学出版社, 2004.
[11]Cox D R. Regression models and life-tables[J]. Journal of the Royal Statistical Society Series B(Methodology), 1972,(2):187-220.
[12]Powell J L. Censored regression quantiles[J]. Journal Econometrics, 1986,(1):143-155.
[13]Portnoy S. Censored regression quantiles[J]. Journal of the American Statistical Association, 2003,(464):1001-1012.
[14]李文娟. 中国ST企业的生存分析的实证研究[D].厦门:厦门大学, 2006.
[15]龚凯颂,焦菲. 企业风险与财务困境预警分析——基于ST德棉的案例分析[J].财会通讯,2012,(27):111-113.
[16]吕院朋. 基于Cox模型的我国房地产上市公司财务困境预警研究[D]. 西安: 西北大学, 2014.
[17]郭爱梅. 企业财务风险的识别分析[J]. 经营管理者,2014, (3):238-239.
[18]孙志猛. 删失分位数回归模型基于扩展兴趣信息准则的平均估计[J]. 中国科学:数学,2014,(8): 857-874.
(责任编辑谢媛媛)
Analysis of Factors Affecting Financial Distress of Listed Companies in China Based on Censored Quantile Regression Model
JIANG Cui-xiaa,b,ZHAO Yia,XU Qi-faa,b
(a.School of Management; b.Key Laboratory of Process Optimization and Intelligent Decision Making of Ministry of Education, Hefei University of Technology, Hefei 230009, China)
Abstract:The Cox proportional hazards model for survival analysis is often applied to studying the problem of financial distress. However, this model needs two difficult assumptions on the behavior of conditional survival functions. So the censored quantile regression model is introduced to survival analysis. The modeling on survival times is made directly with interpretable regression coefficients, which improves the interpretability of the model. It not only provides an effective way for survival analysis, but also is able to identify the key factors affecting the financial distress of listed companies correctly. The results of empirical analysis on listed companies in China show that the censored quantile regression model performs better than the Cox proportional hazards model in the study of financial distress.
Key words:financial distress; survival analysis; censored quantile regression; ST firms
中图分类号:F224.0
文献标志码:A
文章编号:1008-3634(2016)01-0015-10
作者简介:蒋翠侠(1973-),女,安徽砀山人,副教授,硕士生导师。
基金项目:国家自然科学基金项目(71071087);教育部人文社会科学研究规划基金项目(14YJA790015)
收稿日期:2015-07-06

