数形结合方法在高中数学教学中的应用

◆卜艳波

(黑龙江省绥化市第二中学)

数形结合方法在高中数学教学中的应用

◆卜艳波

(黑龙江省绥化市第二中学)

随着我国教育改革工作的不断开展，高中新课程标准也在不断更新，培养学生能力、提高教学质量就成了中学数学教师首先研究的课题。如何开展高中数学教育工作已经成为教育部门和所有中学数学教师们共同关注的问题。在教学中用好数形结合方法不仅能提高课堂教学质量，提高高中生学习数学的能力，无论教还是学都会达到事半功倍的效果，针对数形结合方法在高中数学教学中的应用进行分析，为其他高中数学教育工作者提供参考。

数形结合 高中数学教学 应用

数学是高中课程中重要的-门学科，一直以来也是重点考察的科目。数学也是我们解决实际问题的工具，在科学技术迅猛发展的时代，数学起着越来越重要的作用，在各个相关领域中，也做了突出贡献。但是在单纯只为了追求分数的应试教育下，使得不少学生形成了一种片面的思想共识：数学是一门非常枯燥的抽象学科经过教学实践，认为数学思想方法可以改善数学在学生心中枯燥的形象。数学思想方法也是新课程教材知识体系的灵魂。那么，如何将数学思想方法灵活有效地运用于高中数学教学当中，成了我们数学教师重点研究的课题之一。

一、数形结合的定义

数学的研究对象是现实世界数量关系(数)和空间形式(形)，“数”体现了数量的关系，而“形”体现了空间的形式。数和形常常相互依存，抽象的数量关系常有直观的几何意义，而直观的图形性质也常由数量关系加以描述。数和形在一定条件下互相转化。我们在研究数量关系时，需要借助于图形直观地去研究：而在研究图形时，需要借助数量关系去探求。数和形是研究数学的两个方向，华罗庚教授对此有精辟概括：“数无形，少直观；形无数，难入微。”数形结合可以使数和形统一起来。数形结合是高中数学所蕴含的最基本的思想方法，运用数形结合解题就是在解决有关数量的问题时，根据数量画出相应的几何图形，将其转化为几何，即“由数化形”.解决有关几何图形的问题时，根据图形写出相应的代数信息，将其转化为代数问题，即“由形化数”，从而利用数形的辨证统一和各自的优势得到的解题方法。数形结合是数学中非常重要的思想和解决问题常用的方法，数形结合根据数学阃题的条件和结论之问的内在联系，分析其代数含义的同时，又揭示了其几何直观。数形结合方法在解题的过程中应用十分广泛，它给我们解决问题带来一个全新的思路，由形想数，利用“数”来研究“形”的各种性质，寻求规律，可以从不同的角度培养思维的灵活性，简化解题的思路。用此方法常常可以使所要研究的问题化难为易，化繁为简，思维广阔。

二、数形结合方法在高中数学教学中的应用

三角函数是描述周期运动的重要数学模型，它也是非常重要的函数，是高中课程的重要组成部分，三角函数是数形结合的产物，是描述一般周期函数的基础。

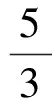
分析：在教学的过程中，学生的做法很多，各不相同，但总起来，就是高中的两种定义求解的，只不过使用定义1的同学取得数据不同而已。下面列举两种方法：

方法一，如图：

解析：初中学习我们就接触过三角函数，在高中仍然作为重点课程来学习，概念的定义就要用到数形结合的思想，这样方便学生形象地记忆。本题在直角坐标系中在角5/3π上任取点p，画一条辅助线AP，得到-个三角形Rt△PAO，通过各点的坐标得出各线段的长度，在根据定义1，知道所求角的正弦、余弦和正切值，我们可通过作图画辅助线，清晰直观的帮助我们快速解题。

方法二；如图

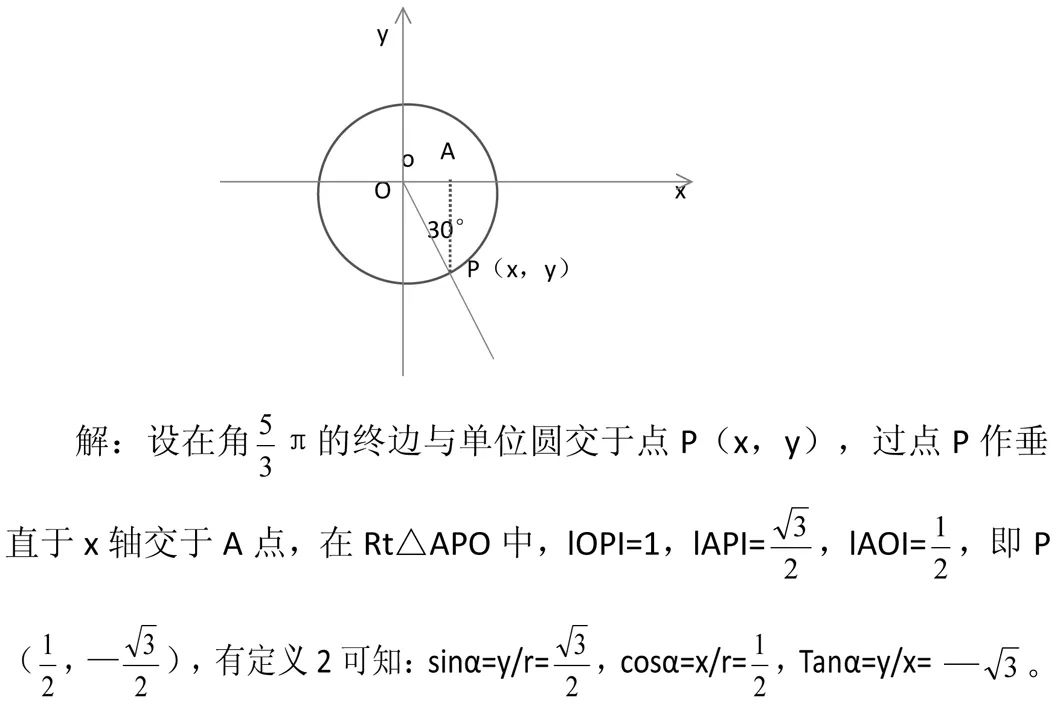
解析：本题运用单位圆这一数形结合方法，贯穿于必修4的定义、公式的推导及应用等整个教学过程中。数形结合应用单位圆非常广泛，能方便、快捷的解决实际问题。是我们学习数学解决问题的有效方法。首先画一个与角相交的单位圆，做一条垂线PA垂直于x轴，根据三角函数的性质，在单位圆里的特殊性质就可以简便的计算出所求角的正弦、余弦和正切值，上述两种方法都用了数形结合思想，但方法二比方法一更为简便，求出P点横纵坐标就能得出结果。

三、结论

通过数形结合方法引导学生思维方式由静态转变为动态，运用动态的思维方式研究问题，能更准确的把握事物的本质。在教学中应用数形结合方法是将数与形巧妙地结合起来，能够提高分析和解决问题的能力。数学的教学过程中重视数形结合方法的教学与研究，数形结合方法是数学思想方法的核心，它提高教育质量的同时还能有效的发挥数学的教育本质，促进素质教育的发展。在高中的教学过程中应用数形结合方法让学生了解并且掌握这一基本思想方法。加强数形结合方法的学习可以使学生理解枯燥乏味且抽象的数学概念，有利于学生认识数学的本质。学生不用死记硬背、生搬硬套，靠记忆模仿，也不用搞题海战术，增加记忆来应付考试。数学学习过程就是一种认知过程，数形结合方法使知识和知识联系起来，深化了学生对认知的认识同时优化了认知结构，教师也有效的提高了教学质量，我们教师在平时的教学中都应该运用数形结合方法，不断研究和发现应用的策略。

[1]缪诣欣.利用数形结合解复数问题[J].中学教学参考，2014，(20).

[2]李春长.谈数形结合在高中数学中的应用[J].课程教育研究，2015，(02).

[3]罗增儒.数形结合：一个解题案例的再分析(续一)[J].中学数学教学参考，2006，(09).

[4]孔宪荣.数形结合思想在高中数学中的应用探究[J].高中数理化，2015，(12).

[5]王鑫.数形结合在初中数学课堂教学中的应用[J].考试周刊，2015，(36).

[6]石慧英.动中求静静中探动—一道动态几何题的解析与思考[J].初中数学教与学，2015，(19).