一种空间库伦土压力计算方法

张 磊 陶伟明 曾宏飞

(中铁二院工程集团有限责任公司， 成都 610031)

一种空间库伦土压力计算方法

张 磊 陶伟明 曾宏飞

(中铁二院工程集团有限责任公司， 成都 610031)

经典库伦土压力理论将挡土墙简化为平面模型，没有考虑挡土墙长度对土压力的影响。由于存在土拱效应，有限长度的挡土墙具有明显的空间效应。文章采用了一种新的空间库伦土压力计算方法，拓宽了空间库伦土压力理论的工程应用范围，并界定了该理论适用的挡土墙长高比范围。挡墙长高比K介于临界值Kn至5之间时，应采用空间库伦土压力理论进行计算，长高比大于5时可采用经典库伦土压力理论。与经典土压力强度的线性增长不同，空间库伦土压力强度与挡土墙高度呈非线性增长，其值小于经典土压力强度。因此，按空间库伦土压力理论进行挡土墙结构设计，具有良好的经济效益。

空间效应； 库伦土压力； 计算方法

1 引言

挡土墙承受的主要荷载是土压力，土压力理论计算始于1773年，库伦(C.A.Coulomb)发表了以挡土墙背滑裂体整体极限平衡为条件的著名库伦土压力理论，其后，1857年郎肯(W.J.M.Rankine)又发表了以微分土体极限平衡理论为条件的郎肯土压力理论。这两种理论成为学术界和工程界至今仍一直广泛应用的最重要的土压力理论。此后，许多学者又相继采用理论、数值、试验等方法对土压力进行了研究，提出了许多新的理论和计算方法[1-3]。

经典的库伦和郎肯土压力理论都是将挡土墙作为平面问题来研究，即将挡土墙看作是无限长挡墙中的一个单位条带，不考虑挡墙长度对土压力的影响。但实际上，挡土墙始终是有限长的，挡土墙和墙背土体的组合不是平面问题，而是一个空间问题。大量研究表明，有限长的挡土墙土压力具有明显的空间效应。本文的空间效应是指，在一定条件下，将土体滑裂体作为一个空间结构而不是平面结构进行土压力计算，更接近于真实情况。

将墙背土体视为松散介质体，应力的传递是依靠介质接触面间的相互作用来进行的。当挡土墙向前产生微小位移时，垂直于挡墙方向产生了微小变形或应力松弛，与之正交的另一个方向，即挡墙长度方向，极易形成拱的作用，当变形达到一定值后，土体的拱效应达到极限，形成极限平衡拱。在平衡拱范围内的土体产生明显的变形，而在平衡拱以外的土体，并未由于墙体的位移而发生明显变形。由于土拱效应的存在，墙背土体滑裂体的体积小于经典库伦模型的体积；挡墙的长高比越小，其滑裂体体积与经典库伦模型的体积相比就越小，土拱效应越明显，空间土压力就越小；当长高比足够大，挡墙足够长时，难以形成土拱效应，空间土压力接近经典库伦土压力。对于长度和高度相当的挡土墙，其空间特性尤其明显，开展空间库伦土压力的研究并运用于工程实际，具有重要的意义。

土压力的空间特性很早为学术界和工程界认识，早在20世纪30年代，在太沙基、契波塔廖夫等的著作中，就已经指出了土压力的空间特性；从50年代开始，很多学者发表了相关研究成果，滑裂体的形状是研究的重点。1952年，波布里科夫首次提出了墙面绝对光滑的有限长度挡土墙上无黏性土的土压力近似计算方法；1976年索柯洛夫认为有限长挡土墙产生微小水平位移时，与库伦所假定的三角形楔体完全不同，认为墙背土体所形成的滑裂体形状是一个梯形角椎体，并据此提出了空间土压力计算方法。但索柯洛夫理论中将滑裂体平截面假定为等腰梯形，且斜边与底边的角度假定为45°，这是缺乏依据的，其角度应与土体的性质有关，不同土体角度不一致。1977年克列恩提出滑裂体是一个半圆柱形截柱体，并据此提出了土压力的计算方法；1978年卡斯台德假定滑裂体是一个抛物线截柱体；1986年捷拉茨通过试验获得了挡土墙背后滑裂体的形状，并指出滑裂体形状与挡墙的长高比有关；1981年到1986年，顾慰慈等曾对挡土墙背后的滑裂体形状进行了系统研究，认为挡土墙背后会形成极限平衡拱，滑裂体的平面是抛物线，滑裂体上半部分是竖直的等截面平衡拱柱段，下部是一个复杂的曲线形截柱体，竖直平衡拱柱段的高度与挡土墙的长高比有关[1]。

由于推导公式极为复杂，求解困难，以上理论只考虑了墙背土体为平坡的情况，限制了工程应用的范围，且没有对空间土压力理论适用的挡土墙长高比范围做出准确的界定。本文结合顾慰慈理论在索柯洛夫方法的基础上进行了新的研究。

2 空间库伦土压力计算理论

2.1 空间库伦土压力计算模型及理论推导

根据顾慰慈教授研究的土压力理论[1]，并考虑挡土墙背后土体为斜面的情况，本文假定挡土墙背后的空间滑裂体为梯形楔体，形状如图1所示，其中图1(a)为立体示意图，图1(b)为正面示意图。墙背的滑裂面均假定为平面，平面ABC和A′B′C′为滑裂体的两侧面，平面CC′B′B为滑动面，滑动面与水平面的倾角为θ。挡土墙背后的极限平衡拱形状一般为抛物线，此抛物线在挡墙两端的切线方向与挡墙长度方向夹角为90°-φ。本文将滑裂体简化为一等腰梯形，如图1(c)所示。由于土体中将形成卸荷拱，滑裂体与卸荷拱的接触面上是不存在应力的，整个滑裂体上仅作用有滑裂体的重力W，滑动面CC′B′B上的反力R，挡土墙墙面对滑裂体的反力E。其中R与滑动面的法线成φ角(φ为填土的内摩擦角)，E与墙面法线成δ角(δ为填土与墙面的摩擦角)，其受力模型如图1(d)所示。

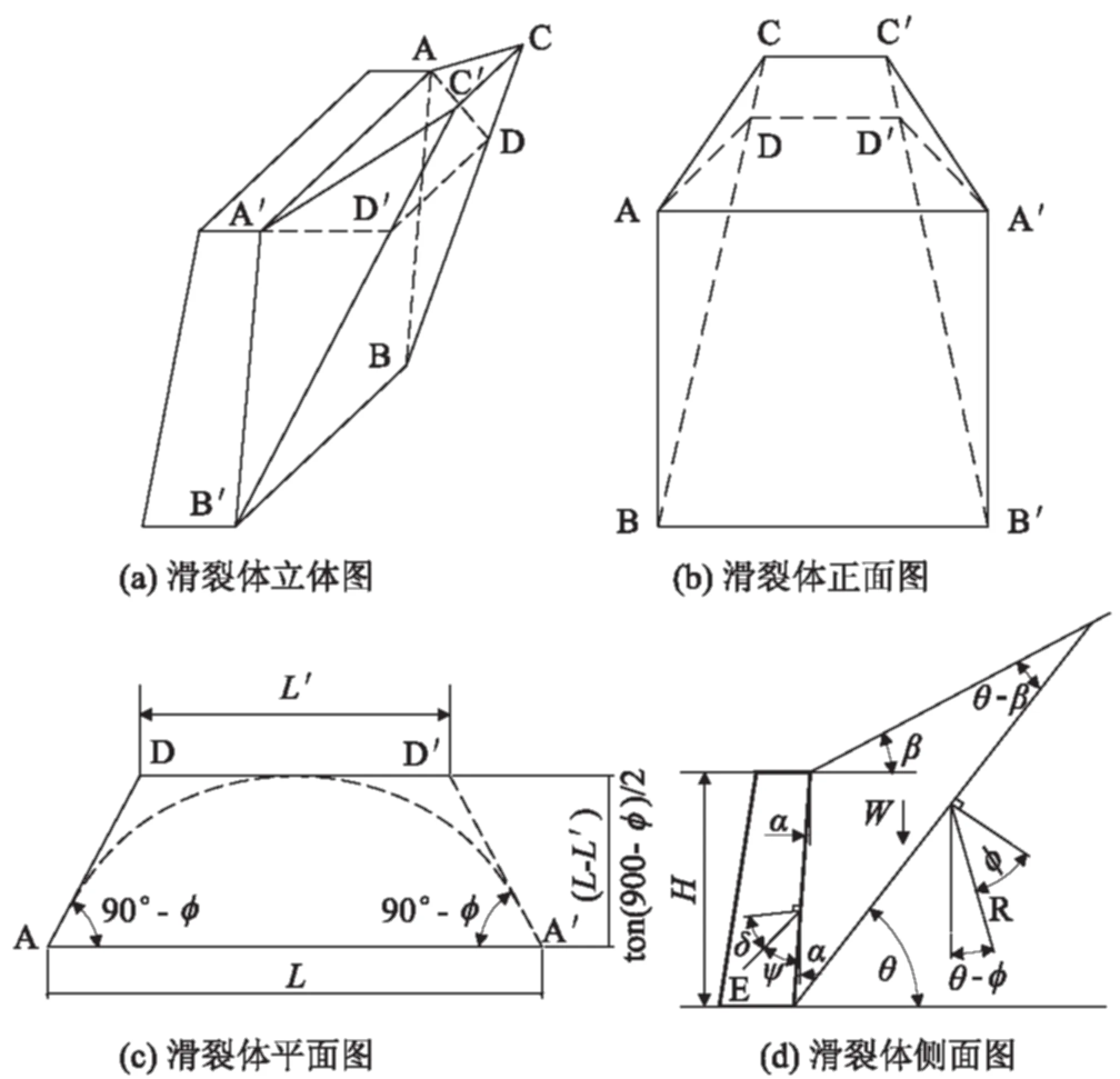
图1 挡土墙背后滑裂体形状示意图

根据几何关系可知，W与E之间的夹角ψ=90°-δ-α，δ与α为已知量，所以ψ为常数，利用正弦定理可得：

(1)

则：

(2)

又，梯形楔体的重力为：

(3)

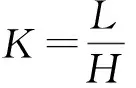
(4)

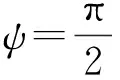
(5)

墙背土体破裂角为：

(6)

总土压力为：

(7)

其中，a=-3Ktanφ,b=(4+6K)tan2φ,c=(2+3K)tanφ-6tan3φ,d=-4tan2φ。

对于复杂的情况，在特定α、β、φ、Κ的参数下，本文采用数值解法并结合物理意义得到破裂角θ，把解出的破裂角θ代入公式(5)，即可求出空间挡土墙的主动土压力E。将总土压力沿着挡墙长度平均化，写成与传统土压力一样的公式结构，即：

(8)

定义λ’为有限长度挡土墙的空间土压力系数。经典库伦土压力系数λ与挡墙的长高比无关，但空间土压力系数则与挡墙长高比相关。以挡墙胸坡α=10°、墙顶土体坡度β=20°为例，分别计算土体计算摩擦角为φ=30°、φ=40°、φ=50°的3种情况，这3种情况的经典库伦土压力系数λ分别为0.323、0.176、0.088。空间主动土压力系数随挡墙长高比K的变化关系如图2所示，部分空间主动土压力系数的值如表1所示。

图2 空间土压力系数随挡土墙长高比的变化关系

不同挡土墙长高比、不同内摩擦角的空间土压力系数如表1所示。

表1 空间土压力系数与经典土压力系数表

由图2、表1可以看出，当挡土墙的长高比极小时(K<1)，空间土压力系数λ’远小于经典库伦土压力系数λ，表明挡土墙所受的总土压力也远小于经典库伦公式得到的土压力；随挡墙长高比的增加，空间土压力系数逐步接近经典库伦土压力系数，总土压力也接近经典库伦土压力。当挡土墙足够长时，空间土压力系数与经典库伦主动土压力系数完全一致，土压力大小也完全一致。

从工程应用的角度，当挡墙的长高比小于5时，有限长挡墙的土压力小于经典库伦土压力，应考虑有限长的挡土墙的空间效应，按空间土压力理论进行计算；当挡土墙长高比大于5时，其空间效应减小，接近无限长挡土墙的受力特点，可按经典库伦土压力进行计算。

2.2 空间库伦土压力理论适用的挡土墙长高比范围

(9)

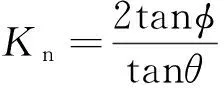
表2 不同参数下的挡土墙临界长高比Kn

从表2中可以看出，挡土墙临界长高比主要与土体的计算摩擦角相关。一般情况下，挡土墙的临界长高比可采用0.5～0.6。挡墙结构的长高比小于临界值时，其滑裂体形状发生了变化，本文的理论误差较大，需进一步研究完善。

综上所述，在工程应用层面，当有限长度的挡土墙长高比K小于临界值(约0.5～0.6)时，本文的方法不直接适用；当长高比K介于临界值(约0.5～0.6)至5之间时，应考虑挡土墙的空间效应，可采用本文的空间库伦土压力理论进行计算；当长高比K大于5时，可采用经典库伦土压力理论。

2.3 有限长挡土墙空间土压力强度沿墙高的分布形式

根据前述公式推导，单位长度挡土墙的土压力为：

(10)

沿墙高的分布形式求导可得到：

(11)

其中，空间土压力系数与挡墙长度L、高度H相关。由于解析解过于复杂不易得到，本文结合数值方法编程计算。以挡墙胸坡α=10°、墙顶土体坡度β=20°、土体计算摩擦角φ=30°、土体重度γ=20 kN/m3为例，分别计算长度为L=3 m、L=5 m、L=10 m的3种挡墙的土压力强度随挡墙高度H的变化情况。

图3 不同长度挡墙土压力强度沿墙高的分布形式

由图3可以看出，在γ、α、β、φ为定值的条件下，空间土压力强度σ随着挡土墙高H的增加，在某一阶段内增加，之后逐渐变缓，最终趋于一极限值。而传统的库伦土压力强度σ随着挡土墙高度H的增加，一直呈线性增加。2种公式所得的土压力强度有显著区别。另外由图3也可以看出在γ、α、β、φ为定值的条件下，挡土墙长度L越大，其空间效应逐渐越小，空间土压力强度σ的值也越接近经典库伦土压力的强度值。

3 结束语

本文结合索柯洛夫和顾慰慈空间土压力理论，在索柯洛夫空间土压力理论基础上加深了研究，将其范围拓展至挡墙墙背为仰斜、墙背土体为斜坡常用的工程情况，并提出了空间库伦土压力理论适用的挡土墙长高比范围。当有限长度的挡土墙长高比K小于临界值(约0.5～0.6)时，本文的方法不直接适用；当长高比K介于临界值(约0.5～0.6)至5之间时，应考虑挡土墙的空间效应，可采用本文的空间库伦土压力理论进行计算；当长高比K大于5时，可采用经典的库伦土压力理论。由于土拱效应的存在，空间库伦土压力小于经典库伦土压力，其土压力强度沿墙高的分布不同于经典土压力强度的线性增长，而是增加到一定程度后基本不变，其值小于经典土压力强度。按本文的空间库伦土压力方法进行挡墙设计，将产生明显的经济效益。

[1] 顾慰慈.挡土墙土压力计算手册[M].北京:中国建材工业出版社，2004. GU Weici. Manual of Earth Pressure Acted on Retaining Wall [M].Beijing:China Building Materials Press， 2004.

[2] 茅以升.茅以升科技论文选[M].北京:中国铁道出版社，1995. MAO Yishen. Mao Yisheng Scientific & Technical Anthology[M].Beijing:China Railway Publishing House,1995.

[3] 朱百里，沈珠江.计算土力学[M].上海:上海科学技术出版社，1990. ZHU Baili，SHEN Zhujiang.Computational Soil Mechanics[M]. Shanghai:Shanghai Scientific & Technical Publishers,1990.

[4] 周佳媚.隧道洞门结构土压力的研究[D].成都:西南交通大学,2004. ZHOU Jiamei. Study of Earth Pressure Acted on Tunnel Portal Structure[D]. Southwest Jiaotong University,2004.

[5] 铁道部第二勘测设计院.铁路工程设计技术手册(隧道)[M].北京:中国铁道出版社，1995. CREEC. Railway Engineering Technical Manual(Tunnel)[M].Beijing:China Railway Publishing House,1995.

[6] TB 10003-2005 铁路隧道设计规范[S]. TB 10003-2005 Code for Design of Railway Tunnel[S].

A Calculation Method of Spatial Coulomb Earth Pressure

ZHANG Lei TAO Weiming ZENG Hongfei

(China Railway Eryuan Engineering Group Co.,Ltd., Chengdu 610031,China)

The classical Coulomb earth pressure theory simplifies the retaining wall to plane model, without considering the impact on the earth pressure of retaining wall length. There is obvious spatial effect for the retaining wall with finite length because of soil arching effect. This paper uses a new calculation method of spatial Coulomb earth pressure, and broadens the engineering application range of spatial Coulomb earth pressure theory, and defines the range of length height ratio of the retaining wall. If the length height ratioKis betweenKnand 5, spatial Coulomb theory is adopted to calculate earth pressure. If the length height ratio K is greater than 5, the classical Coulomb theory is suitable. Unlike the linear growth of the classical earth pressure strength by , the spatial Coulomb earth pressure strength is nonlinear growing with the height of retaining wall, its value is less than the classical earth pressure strength. It is economical to design retaining wall with spatial Coulomb earth pressure theory.

spatial effect； Coulomb earth pressure； calculation method

2015-04-15

张磊(1985-)，男，工程师。

1674—8247(2016)01—0006—04

TU432

A