基于季节性马尔科夫模型的郑州市降雨指数衍生品定价

王志良, 鲁亮涛， 刘萍萍

(1.华北水利水电大学,河南 郑州 450045; 2.鹤壁市盘石头水库建设管理局，河南 鹤壁 458030)

基于季节性马尔科夫模型的郑州市降雨指数衍生品定价

王志良1, 鲁亮涛1， 刘萍萍2

(1.华北水利水电大学,河南 郑州 450045; 2.鹤壁市盘石头水库建设管理局，河南 鹤壁 458030)

未来特定时间区间内降雨指数的微小差别,会对降雨指数衍生品的理论价格产生很大的影响。根据郑州市的降雨过程具有明显的季节性特征的特点,提出了季节性马尔科夫模型,并用此模型对其降雨频率进行建模。然后,用Gamma分布模拟郑州市不同季度的日降雨量的分布。最后,对郑州市未来一年的日降雨量进行随机模拟,并运用蒙特卡洛方法,模拟计算了基于郑州市第二季度降雨累积指数的期货合约的到期收益值。计算结果表明,本文提出的季节性马尔科夫模型可以更好地模拟郑州市降雨过程的统计特征。

天气衍生品;季节性马尔科夫模型;累积降雨指数;蒙特卡洛模拟

降雨指数衍生品是一类金融衍生工具，主要用来管理和控制极端天气风险。与气温指数衍生品定价问题[1-2]相比,降雨指数衍生品定价的主要难点是建立精确的降雨预测模型[3-4]。使用目前的气象学模型[5]预测降雨可以得到较好的预测结果，但是气象学模型比较复杂,并且预测的时间区间有限。因此,应用统计方法解决降雨量的预测问题很有意义。

降雨过程的统计规律比较复杂[6],精确地计算未来某一时段的降雨量具有很大的难度。学者们运用了很多统计学方法对此问题进行了研究。文献[7]用人工神经网络模型对降雨过程进行建模，该模型使用温度、湿度、风速等因素预测未来可能的降雨量。在2014年,Masala用马尔科夫模型对降雨频率序列进行了研究[8]。人工神经网络模型和马尔科夫模型,都可以提取降雨量序列的部分统计特征,但其相关性的时间滞后项有限,很难提取日降雨量序列在年时间尺度的季节性特征。

为了更好地提取降雨量序列的季节性特征,本文提出季节性马尔科夫模型，并将其应用于郑州市降雨指数衍生品的定价中。

1 郑州市降雨统计特征

河南省是我国的产粮大省,研究郑州市的降雨指数衍生品定价问题具有很好的现实意义。本文以郑州市1985—2014年日降雨数据集为样本,数据来自“中国地面国际交换站气候资料日值数据集”。

研究郑州市降雨指数衍生品定价问题,首先应研究郑州市降雨序列的统计特征。将数据集中30 a的日降雨量序列分为365组,第i组包含每一年中第i天的降雨量数据,计算每一组的平均值,得到郑州市一年中各天的平均降雨量，如图1所示。

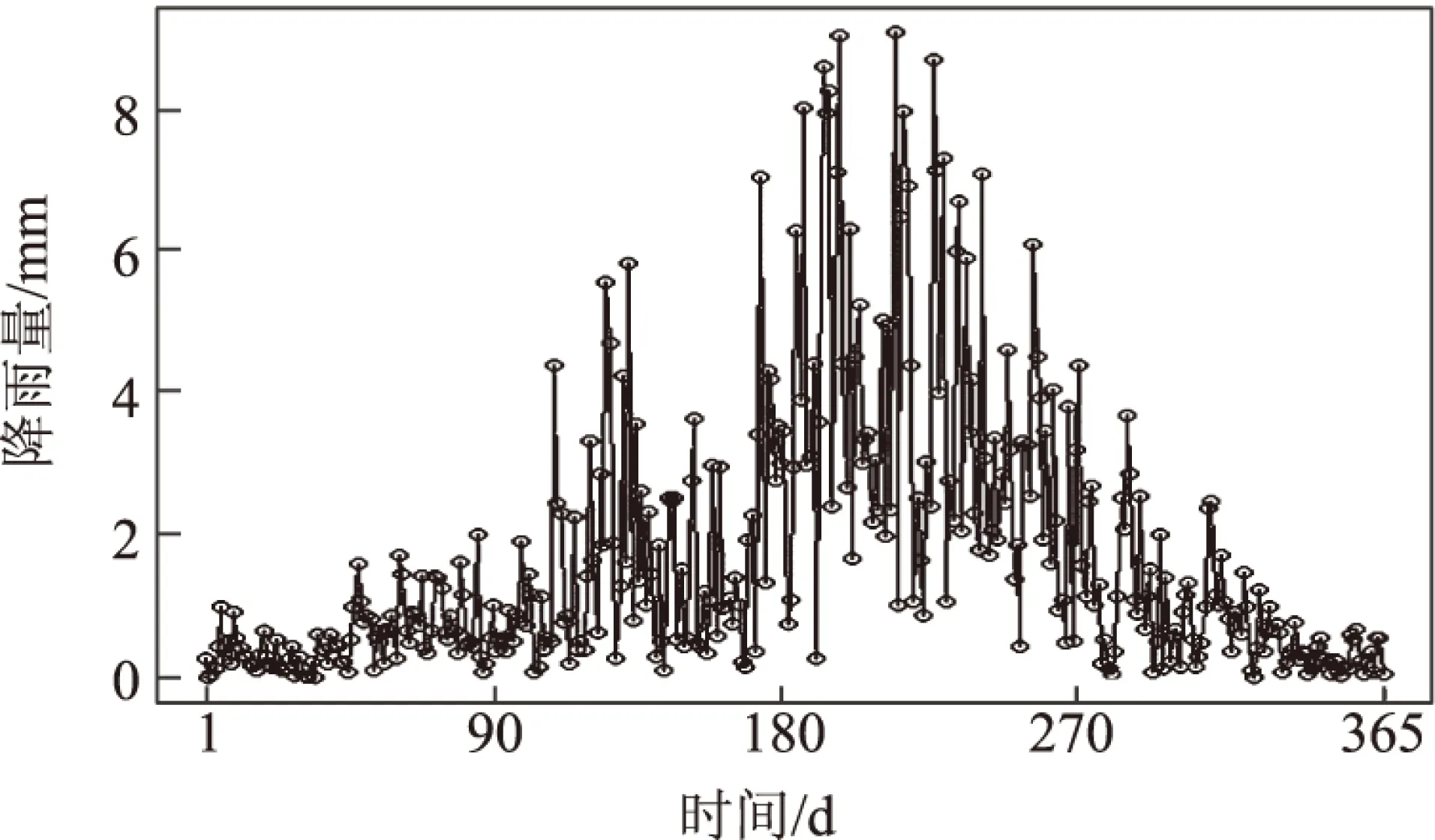
图1 郑州市30 a的日平均降雨量

从图1中可以看出,郑州市日平均降雨量呈现出第一季度和第四季度降雨量较少,第二季度和第三季度的降雨量较多的特征。郑州市日平均降雨量序列具有明显的周期性。

2 季节性马尔科夫模型

与一阶马尔科夫模型一样,一阶季节性马尔科夫模型满足无后效性,即满足下式[9]:

(1)

式中：t=1,2,…,T；T为随机过程{Xt}的周期。这里所说的周期的意思是随机变量Xt的分布列与随机变量Xt+T的分布列相同。

对于两状态季节性马尔科夫模型来说,其转移概率矩阵为：

(2)

式中pjk(t)(j,k=0,1)表示随机过程{Xt}在t时刻处于状态j,在t+1时刻处于状态k的概率。

将时间序列{xt}转换为状态序列{st}。对于郑州市的日降雨量序列,如果某一天降雨量是零,就将其设定为“0”,表示该天没有降雨。如果某一天降雨量不是零,就将其设定为“1”,表示该天降雨。

为了给出转移概率矩阵的一个估算方法,这里需要对状态序列{st}进行一些处理。假设随机过程{Xt}的周期为T,按照周期将状态序列{st}分为n组,每组包含一个周期的数据。然后,将每组中的第i个数据取出来,按时间顺序排序后作为一个向量,用Vi(i=1,2,…,T)表示，例如：

V1=[s1,s1+T,s1+2T,…,s1+(n-1)T]。

对郑州市日降雨状态序列来说,V1就是每年中第1天的状态值按时间顺序排序的向量。

根据季节性马尔科夫模型转移概率矩阵的含义,这里给出它的一个估计方法为：

(3)

式中njk(t)表示在向量Vt中元素为j、在向量Vt+1中对应位置的元素为k的数值对个数。但这里的njk(T)是一种特殊情况,它表示向量Vt中元素为j、在向量V1中对应位置的下一个元素为k的数值对个数。

对于郑州市来说,将30 a的日降雨量数据分为30组,每组包含其中一年的数据,也就是说将周期T设定为365,按上述方法计算其转移概率矩阵,其中p01(t)(t=1,2,…,365)的计算结果如图2所示。图2表明,郑州市一年中晴天转移到雨天的概率与时间有关,从一年中的第1天开始,随着时间的推移,逐渐变大,然后变小。说明季节性马尔科夫模型可以提取郑州市日降雨状态序列的转移概率矩阵的周期性特征。

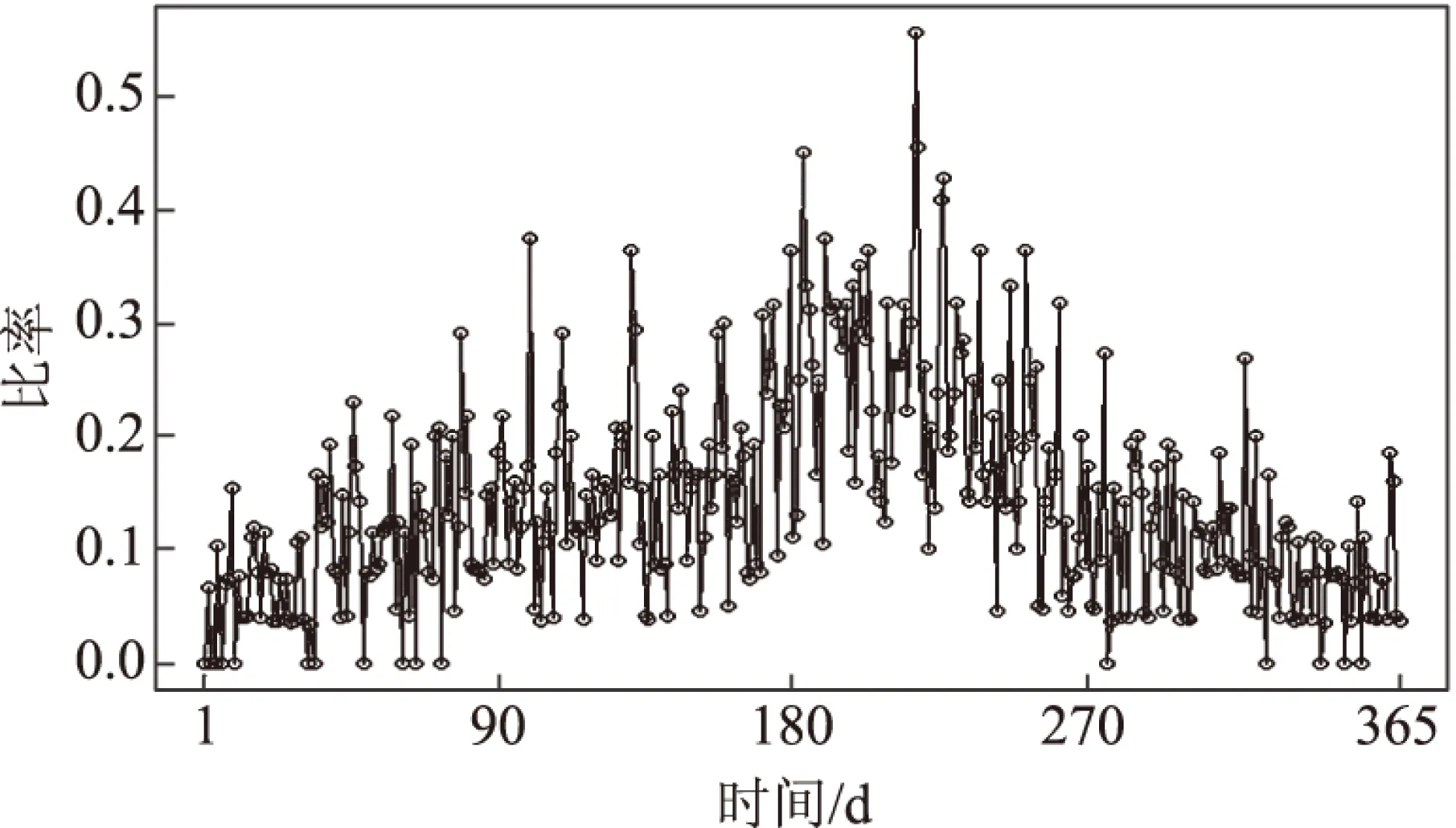
图2 晴天转移到雨天的比率序列

季节性马尔科夫模型可以用来模拟未来一个周期内随机过程{Xt}的状态序列。

首先，估算随机过程{Xt}的初始概率分布列[p0(0)p1(0)]。其中p0(0)表示初始状态为“0”的概率,p1(0)表示初始状态为“1”的概率。这里给出一个估算方法：

(4)

式中Z为状态序列{st}中元素为k的个数,T为状态序列{st}中元素的个数。

然后，计算在未来一个周期内,随机变量Xt在时刻t的概率分布列[p0(t)p1(t)]为：

[p0(t)p1(t)]= [p0(t-1)p1(t-1)]·

(5)

式中t=1,2,…,T。

最后,设定一个参数为λ(0<λ<1),如果p0(t)>λ,就将其对应的状态设定为“0”；否则,就将其对应的状态设定为“1”。这样,就得到了未来一个周期内随机过程{Xt}的状态序列。这里给出一个设置λ的方法：根据历史数据,计算出一个周期内状态处于“0”的平均值。先令λ=0.01，模拟出随机过程{Xt}的1个状态序列，计算状态为“0”的元素个数M；然后以0.01为步长增加λ的取值，重复前述计算过程，直到λ=0.99,得到99个模拟的M；当模拟的M值与历史数据计算的状态处于“0”的平均值最接近时，λ就取对应的值。

3 降雨量模型

模拟计算降雨量序列,除了需要得到是否降雨的状态序列,还要模拟出每天的降雨量。降雨量数据都为大于等于零的值,郑州市日降雨量又具有非对称、右偏的特征。因此,用Gamma分布来描述郑州市日降雨量是合适的。其概率密度函数为：

(6)

式中：α为形状参数；β为尺度参数；Γ(α)为Gamma函数在点α的值。

Gamma分布的极大似然函数为：

(7)

对极大似然函数L(α,β)求对数,然后分别对α和β求偏导数,并令偏导数等于零,可得到Gamma分布的极大似然估计：

(8)

(9)

(10)

4 郑州市降雨指数衍生品定价

芝加哥商品交易所是全球衍生品交易最为活跃的交易所之一,基于日降雨量累积指数CR的降雨指数衍生品合约是其天气市场的重要组成部分。

日降雨量累积指数CR指的是在时间区间[τ1,τ2]内的降雨总量,其计算式为：[9]

(11)

式中Y(t)为日降雨量序列。

计算郑州市降雨指数衍生品的到期收益值,首先要模拟计算郑州市未来某一时间区间的日降雨量序列。郑州市日降雨量序列具有以年为周期的特征,因此,这里设定季节性马尔科夫模型中的周期T为365 d。用郑州市1985年到2014年的日降雨量序列,可以计算出季节性马尔科夫模型的转移概率矩阵Mt(t=1,2,…,365)。这里给出M1，即：

由于郑州市日降雨量极不均匀,这里将郑州市日降雨量样本分为4个集合,第i个集合包含第i个季度的样本。然后分别估计相应的Gamma分布的参数,结果见表1。

郑州市1985—2014年的年平均降雨天数为76.9 d，取整后为77 d。将参数λ设为0.69时，模拟出的年平均降雨天数为52 d；将参数λ设为0.70时，模拟出的年平均降雨天数为78 d。综合考虑，将参数λ设为0.70，然后模拟计算出郑州市2015年降雨频率序列。

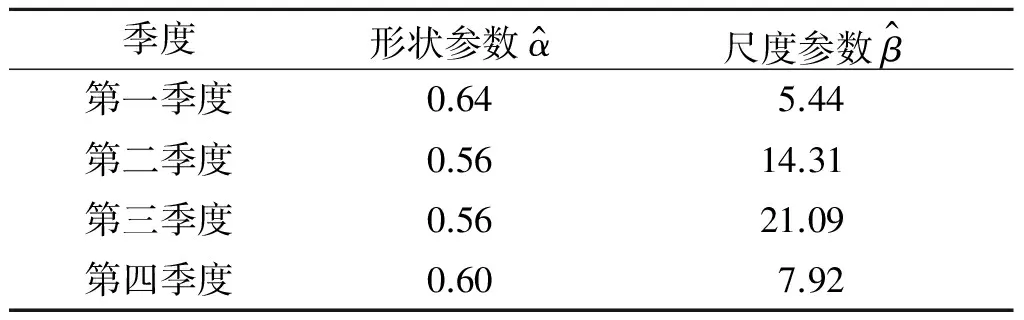
表1 四个季度的Gamma分布参数的极大似然估计

根据郑州市降雨频率序列和降雨量的Gamma分布,可以模拟郑州市的降雨过程。其具体方法是：如果降雨频率序列的值为“1”,就随机产生一个相应季度的Gamma分布的随机数,作为该天的降雨量。如此模拟郑州市未来一年的降雨过程,计算结果如图3所示。

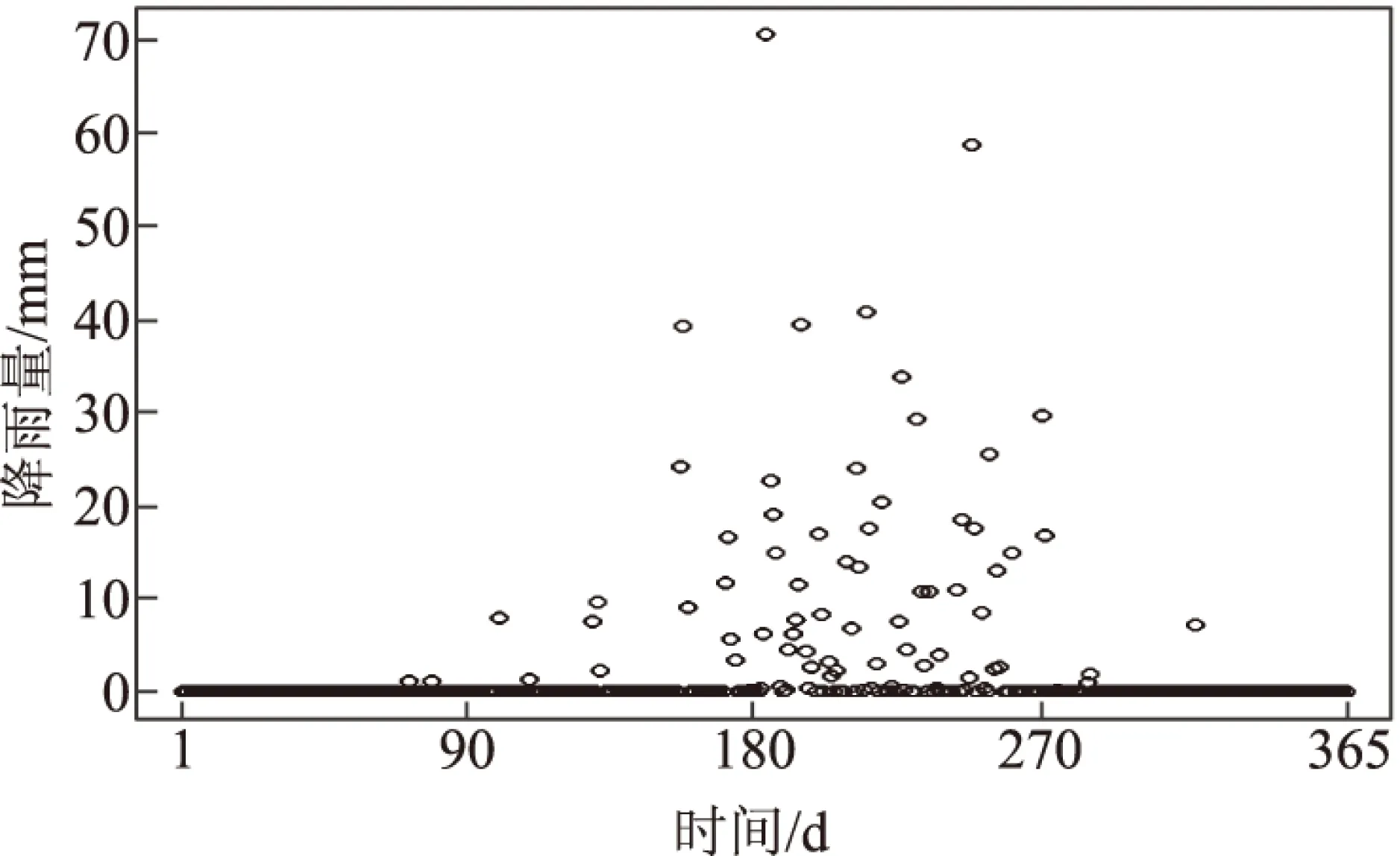
图3 年降雨过程模拟序列

图3表明，季节性马尔科夫模型和分季度的Gamma分布,可以很好地提取郑州市日降雨量的季节性特征。

降雨指数期货合约是降雨指数衍生品的一种,合同规定了在未来某一时刻,交易双方以在签订合约时刻规定的价格交割某种降雨指数。另外，降雨指数期货合约还规定了合约标的、合约乘数、单位、最小变动单位、合约月份、交易时间、交易保证金和交割方式等。

假设一个基于郑州市日降雨量累积指数CR的期货合约,合约月份为2015年第二季度3个月，合约标的是122个指数点,合约乘数为1个指数点10元,最小变动单位为1个指数点,交割方式为用人民币交割。

对于卖方来说,售出一份这样的合约，到期收益值WS由下式给出：

WS=10(CR-122)。

(12)

结合季节性马尔科夫模型和分时段Gamma分布,用蒙特卡洛方法模拟100 000次2015年第二季度的降雨过程,计算卖方相应的到期收益值WS,结果见表2。

表2中的数据表明，对于假设的合约，如果卖方运用本文的模型，计算其售出一份合约，到期收益值为-497元，是亏损的，他将会停止输出此合约，改为售出标的指数较低的合约。

表2 到期收益值WS的均值与方差

5 结 语

降雨指数衍生品是一类重要的金融衍生工具,可以用来对冲极端天气造成重大损失的风险。郑州市降雨指数的统计特征非常复杂,一年之中降雨天数较少,日降雨量的波动性较大。本文提出的季节性马尔科夫模型可以提取第二季度和第三季度降雨天数较多,第一季度和第四季度降雨天数较少的特征。由于一年之中的日降雨量并不平均,第二季度和第三季度的日降雨量相对较大,本文将样本分为4个部分, 不同部分包含不同季节的样本，分别计算其Gamma分布参数,用来描述日降雨量的年周期性特征。结合季节性马尔科夫模型和分季节Gamma分布,本文模拟了郑州市未来一年日降雨量序列,计算出未来降雨指数的期望值。用季节性马尔科夫模型和分时段的概率分布模型,可以较好地提取郑州市日降雨量的季节性特征，从而计算得到合约到期价值的期望值。但是,用此模型得到的合约到期价值的方差较大，需要建立更好的模型,减小计算出的指数的方差。

[1]王明亮,何建敏,曹杰.基于气温指数的我国天气衍生品定价研究[J].数理统计与管理,2015,34(2)：217-223.

[2]孙保敬,李世平.天气指数衍生品及其定价研究[J].统计与决策,2015(5):154-156.

[3]Li A,Cao M,Wei J Z.Precipitation modeling and contract valuation:a frontier in weather derivatives[J].Journal of Alternative Investments,2007,7(2)：15-21.

[4]Djehiche B,Alaton P,Stillberger D.On modeling and pricing weather derivatives[J].Applied Mathematical Finance,2002,9(1):1-20.

[5] Little M A,Mcsharry P E,Taylor J W.Generalized linear models for site-specific density forecasting of U.K.daily rainfall[J].Monthly Weather Review,2008,137(3):1029-1045.

[6]Stowasser M.Modelling rain risk:a multi-order Markov chain model approach[J].Journal of Risk Finance,2011,13(1):45-60.

[7]Ramirez M C V,Velho H F D C,Ferreira N J.Artificial neural network technique for rainfall forecasting applied to the Sao Paulo region[J].Journal of Hydrology,2005,301(1):146-162.

[8] Masala G.Rainfall derivatives pricing with underlying semi-Markov model for precipitation occurrences[J].Stochastic Environmental Research & Risk Assessment,2014,28(3):717-727.

[9]Alexandridis A K,Zapranis A D.The Weather Derivatives Market[M].New York:Springer,2013：241-270.

(责任编辑：陈海涛)

Valuing Rainfall Index Derivatives of Zhengzhou Based on Seasonal Markov Model

WANG Zhiliang1, LU Liangtao1， LIU Pingping2

(1.North China University of Water Resources and Electric Power, Zhengzhou 450045, China; 2.Panshitou Reservior Construction and Administration Bureau, Hebi 458030, China)

During the process of pricing rainfall index derivatives, the minute difference existed in the predicted value of rainfall index in the future specific temporal interval, will significantly influence the theory price of rainfall index derivatives. In the article, we proposed the seasonal Markov model for the obvious seasonal characteristics of rainfall process in Zhengzhou, the rainfall frequency was modeling with this model. Then, the distribution of the daily rainfall in the different season in Zhengzhou was simulated with Gamma. Finally, the daily rainfall of the future year in Zhengzhou was randomly simulated, the yield-to-maturity value of the futures contracts based on the accumulated rainfall index of the second quarter in Zhengzhou was simulated and calculated. The calculation results show that the seasonal Markov model can preferably simulate the statistical characteristics of the rainfall process of Zhengzhou City.

weather derivatives; seasonal Markov model; rainfall index; Monte-Carlo simulation

2016-02-17

河南省科技厅基础与前沿研究(142300410175)。

王志良(1966—),男,河南舞阳人,教授,硕导,博士,主要从事水文水资源研究。E-mail:wzl@ncwu.edu.cn。

10.3969/j.issn.1002-5634.2016.02.005

TV125；O29

A

1002-5634(2016)02-0033-04