城市轨道交通网络系统设计承载能力计算方法研究∗
李晓龙 韩静茹 宋留洋(同济大学铁道与城市轨道交通研究院,201804上海,∥第一作者,教授)
城市轨道交通网络系统设计承载能力计算方法研究∗
李晓龙 韩静茹 宋留洋
(同济大学铁道与城市轨道交通研究院,201804上海,∥第一作者,教授)
摘 要结合城市轨道交通网络系统设计承载能力的概念及特点,全面系统地研究了影响城市轨道交通网络系统设计承载能力的各项因素,并在借鉴以往线路承载能力计算方法的基础上,结合约束理论(TOC),计算了单条线路的承载能力。然后根据系统线网形成的特点,利用分布估计算法建立了城市轨道交通网络系统设计承载能力的计算模型。最后,以上海市轨道交通网络系统为例,对计算模型进行验证。结果表明该模型计算量较小、计算速度较快、可行性较强,并反映了上海市轨道交通网络系统的实际情况。
关键词城市轨道交通网络系统;承载能力;约束理论;分布估计算法;计算模型
“十二五”国家科技支撑计划项目(2013BAG19B00)
Author′s address Institute of Railway and Urban Rail Transit,Tongji University,201804,Shanghai,China
目前,国内外关于城市轨道交通网络系统承载能力的研究相对较少[1-2],尚未有统一的关于城市轨道交通网络系统设计承载能力的定义和计算方法。因此,对城市轨道交通网络系统承载能力和实际需求之间的匹配关系也未有相应的评价体系。在以往的研究中,对城市轨道交通承载能力的分析大多从线路运输能力的角度出发,即:以简单的线路条件为背景,以单位时间内通过的列车对数或输送的乘客人数来表示[3-6],很少涉及大规模网络条件下系统设计承载能力的计算。然而,城市轨道交通系统的基本要素是多个点和多条线,点和线的承载能力是研究轨道交通系统设计承载能力的基础。但一个城市轨道交通系统的承载能力又不仅仅是其中各个点、线子系统能力的简单叠加,而是受点、线间相互关系的共同制约。因此,本文运用系统工程的思想,提出了城市轨道交通网络系统设计承载能力的概念,分析了影响城市轨道交通系统设计承载能力的各项因素,并建立了网络系统设计承载能力的计算模型。
1 城市轨道交通网络系统设计承载能力概述
1.1城市轨道交通网络系统设计承载能力定义
通常人们认为承载能力是一种能力限度,即某系统具有某种能力的极限值。对城市轨道交通系统来说,一个城市的轨道交通网络系统的设计承载能力应该就是这个城市所拥有的城市轨道交通网络系统输送乘客的极限能力。
设C为城市轨道交通网络系统的承载能力, x1,x2,...,xn表示影响轨道交通网络系统设计承载能力的因素。则:
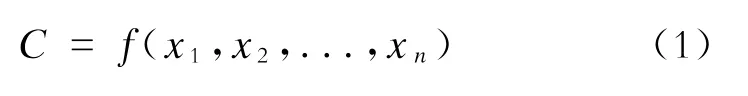
上述影响网络系统设计承载能力的因素x1, x2,...,xn有些来自系统的内部,有些则来自系统的外部环境,内外部因素的共同作用影响着系统效能的发挥,也就直接影响到了网络系统设计承载能力的大小;式中f则表示影响承载能力的各个因素对承载能力影响的方式。
城市轨道交通系统由设备设施(包括线路、车站、供电系统、车辆、信号系统等)、管理制度体系(包括操作规程、工作流程、管理制度等)和人员组成,这些基本单元之间相互关联、相互作用,构成了完整的可以运行的轨道交通网络系统。因此,城市轨道交通网络系统设计承载能力是一个由众多约束条件决定的量,与客流量无关。其具体定义如下:城市轨道交通系统设计承载能力是指在现有设备设施、管理体系、人员和外部条件下,考虑到各车站、线路相互协调及日常随机因素的影响,城市轨道交通网络系统在单位时间内所能提供的乘客的最大运输能力,其单位为万人次/h。为了能清晰地描述系统实际能力的发挥情况,提出了承载强度的概念。承载强度是描述系统能力发挥程度的量,在数值上它是实际客流量与承载能力的比值。设α为系统的承载强度,E为轨道交通网络系统的实际客流量,则:

一般而言,α≤1,当承载强度接近1时,意味着系统的能力接近极限。
1.2城市轨道交通网络系统设计承载能力的影响
因素
分析影响城市轨道交通网络系统设计承载能力的因素,有利于找出影响和提高网络系统设计承载能力的关键环节,进而从整体上优化城市轨道交通系统的运行效率。具体因素如下:
(1)设备设施。从理论上讲,研究城市轨道交通系统的承载能力是以一个固定的系统为研究对象进行分析的,但是随着时间的推移,系统中某些设备的质量会发生相应的变化,致使系统的安全性、可靠性等参数发生变化。另外,在不同的时期,甚至是不同的时段,城市轨道交通运营单位会投入不同数量的设备(例如列车),因而使得系统的能力发生波动,而这必然会导致系统设计承载能力的变化。
(2)管理体系。管理制度体系是城市轨道网络交通运营的重要支柱,包括运营管理、维修管理、安全管理等方面,该体系的优劣将直接影响到整个系统运行的效率和能力。
(3)线网规模与布局。网络系统规模从数量上反映了系统设计承载能力,是形成城市轨道交通系统设计承载能力的物质基础。一般来说,在城市轨道交通运输效率不变的情况下,网络系统规模越大,系统设计承载能力就越大,反之,系统设计承载能力就越小。而在线网布局方面,各线路之间的协调能力、换乘能力等又是影响网络系统能力的关键要素。对于城市轨道交通网络系统而言,因线网布局的不同,同样数量的线路和车站其承载能力是不同的。
2 城市轨道交通网络系统设计承载能力计算模型
2.1基于约束理论的城市轨道交通线路承载能力计算
约束理论(Theory of Constraints,简称TOC),由以色列物理学家戈德拉特博士提出[7]。它的核心在于:任何系统都至少存在一个制约因素,否则它就可能有无限的产出。任何系统都可以想象成由一连串的环所构成,环环相扣,而系统的强度(或者最大能力)就取决于其中最薄弱的一环。
城市轨道交通单条线路承载能力是由线路中各子系统(轨道、车辆、供电、管理制度、人员等)相互作用决定的。因此,基于TOC,可以将城市轨道交通单条线路视为一条链条,每个子系统都是这个链条中的一环,整个线路承载能力的大小则由其中最弱的一环决定。设C线路表示城市轨道交通系统中单条线路的承载能力,x1,x2,...,xn表示线路中各子系统(轨道、车辆、供电、管理制度、人员等)决定的系统设计承载能力,则:
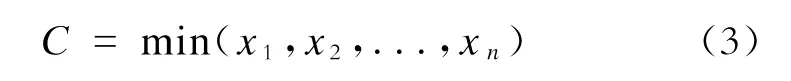
这里,假设系统的轨道、车辆、通信信号和供电的能力综合决定了线路的输送能力,用c线路表示;而设施中车站能力占主要部分,用c普通车站表示,假设管理制度体系能承担的承载能力大于前两者,则由TOC可得:

对于线路的输送能力,设列车运行最小间隔时间为h(min),车辆定员数为P(人),最大允许超员率为σ,列车编组数为m(辆),线路长度为L(km),平均运距为(km),则单位时间内(h)线路输送能力:
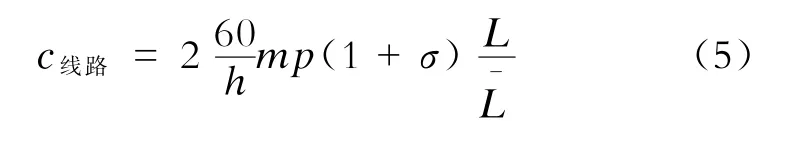
普通车站,站台、通道、楼梯、自动扶梯和自动售检票等设备的能力综合决定了车站承载能力。根据TOC,则车站的最终承载能力:

式(6)中,通道通过能力c通道、自动扶梯输送能力c自扶、自动售票机使用能力c售票、进/出站检票机通过能力c进/出检以及站台容纳能力V站台的具体计算方法可参考文献[1]。
2.2基于分布估计算法的城市轨道交通网络系统设计承载能力计算
分布估计算法是一类基于概率模型的进化算法。该方法用概率模型描述变量之间的相互关系,并通过对该模型随机采样,产生下一代种群,如此反复进行,实现种群的进化,直到满足结束条件才终止。
该方法基于整个群体建立数学模型,直接展现了整个群体的进化趋势[8],对解决非线性、变量耦合的优化问题非常有效。而城市轨道交通网络系统的线网形成过程与种群进化过程类似。系统中各条线路通过换乘站相连,随着线路的增多,换乘站的增加使各线路之间的耦合关系越来越复杂,线路分布处于动态变化中,直接影响整个系统的承载能力。
因此,根据分布估计算法,城市轨道交通系统设计承载能力的计算步骤如下:
第一步,设初始状态下,系统中的线路总数为n 条,各条线路之间的换乘关系用H表示,若线路i与线路j有换乘关系,则Hij为1,反之,Hij为0。
Pi,0为初始状态下线路i与其他线路的可换乘概率:

式中,ki,0为初始状态下与线路i具有换乘关系的线路总数。
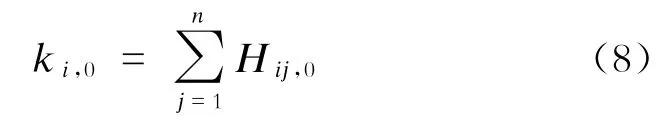
式中,Hij,0为初始状态下线路i与线路j的换乘关系。
第二步,若不存在Pi,a=0或1的线路,则选择换乘概率较高的n线路,a+1条线路(n线路,a+1<n线路,a)组成新的系统,并更新各条线路的换乘概率Pi,1。而对于被去除的线路,此时的换乘概率则为其最终换乘概率。
若存在Pi,0=0或1的线路i,则线路i计算终止,不再参与下一循环,线路i的最终换乘概率为Pi,a-1。而其他线路则组成新的系统,继续循环。
第三步,经过a次循环后(a≥1),系统中所有的线路换乘概率均为0或1时,系统循环终止。
则城市轨道交通网络系统设计承载能力的最终计算结果为:
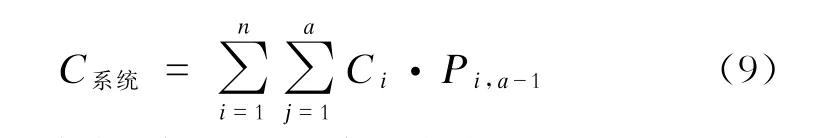
由于城市轨道交通设计承载能力还受设施设备、管理体系以及线路规模等因素的影响,因此设λ为修正因子,则修正后的城市轨道交通设计承载能力:

3 上海市轨道交通网络系统设计承载能力分析
3.1上海市轨道交通网络系统设计承载能力计算
截止到2014年底,上海市轨道交通网络系统由14条线路组成,全网运营线路总长567 km,各条线路的概况如表1所示。共计车站337座,其中换乘站为45座,各线路换乘情况如表2所示。
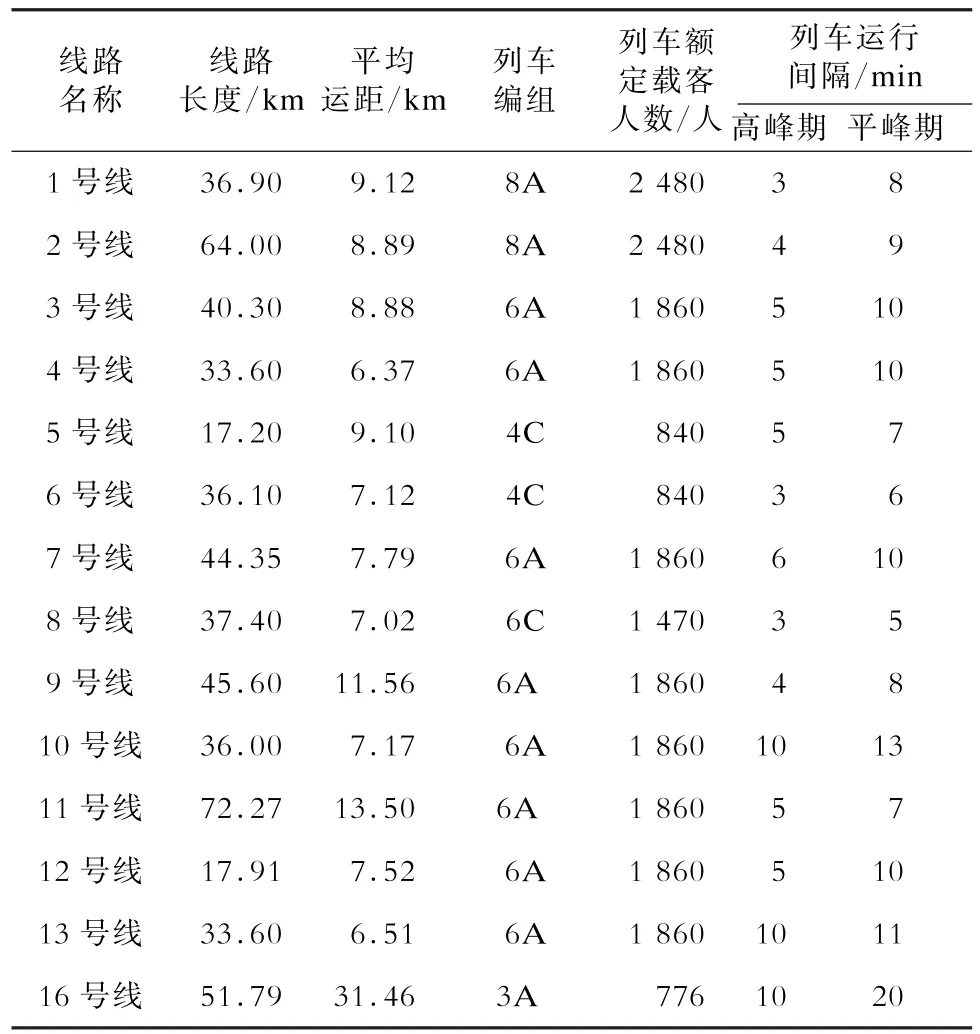
表1 上海市轨道交通网络系统概况
结合上海轨道交通的实际运营情况,为简化计算,设所有线路运营时间为05:30—23:30,历时18 h,其中高峰时段为06:30-09:30,16:00—19:00,共6 h,其余为平峰时段,共12 h。高峰时段列车载客量超出额定载客量20%~80%,平峰时期列车载客量为额定载客量的20%~40%。若考虑其他因素对承载能力的影响,则λ取0.6。因此,根据上述承载能力公式可得上海市轨道交通网络系统设计承载能力的计算结果,如表3所示。

表2 上海轨道交通各条线路之间换乘站 座

表3 上海市轨道交通网络承载能力概况
3.2上海轨道交通网络系统设计承载能力分析
图1反映了上海轨道交通线路日均承载能力的概况,由于线路长度、车站规模、列车编组等因素不同,导致线路承载能力差别很大。
由图2可知,各条线路日均承载强度为10%~50%,其中10号线较为突出,为83%;高峰期承载强度为80%~100%,整个系统处于饱和状态;平峰期承载强度为2%~25%。不同时段承载强度明显不同。由于高峰时段,通勤客流出行集中,而平峰时段,客流仅以市民日常出行、外来旅游、商务客流为主,客流量较少,所以,同一条线路高峰时段的承载强度远远大于日均承载强度以及平峰时段承载强度。同时由于通勤客流大部分居住在线路两端,工作在城市中心区,这种特性带来了城市轨道交通客流的“潮汐”特征,也就是工作日早高峰客流流动方向为市郊→市区,晚高峰客流流动方向为市区→市郊。工作日早晚时段客流流动方向相反,导致不同线路的高峰时段承载强度存在明显差距,承载强度分布不均衡。

图1 上海市轨道交通网络系统线路日均承载能力占比图
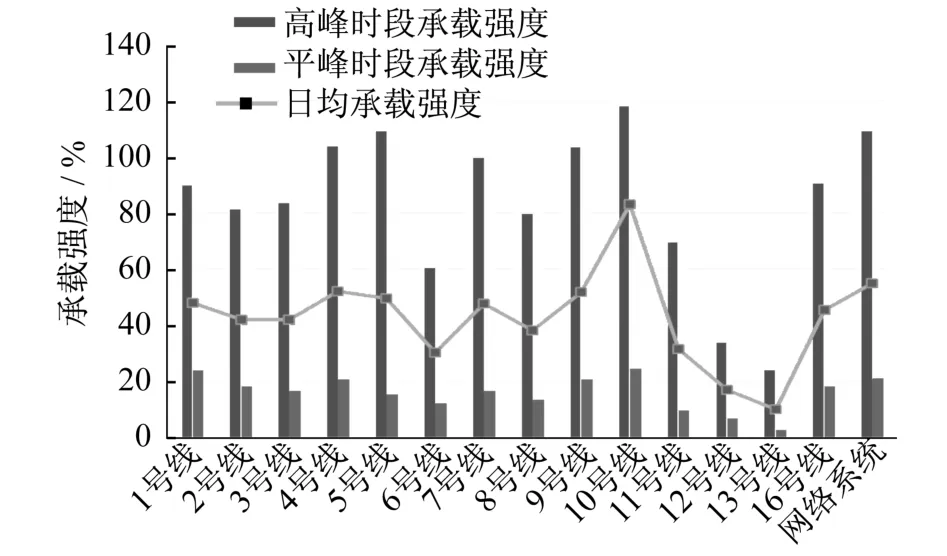
图2 上海市轨道交通系统不同时段的线路承载强度
图3反映了历年来上海轨道交通网络系统设计承载能力和承载强度的变化情况。随着轨道交通线网的不断完善,系统的承载能力在不断增长,同时系统的承载强度也在不断增大,这说明城市轨道交通已经成为了更多市民出行的选择。据相关统计数据统计,目前上海轨道交通网络系统平峰时段上座率不足30%,而计算结果显示系统中各条线路的承载强度均在上座率左右。这较好地反映了上海轨道轨道交通的现状,同时也进一步验证了该计算模型的可行性、有效性。
4 结语
针对城市轨道交通网络系统的特点,本文给出了城市轨道交通网络系统设计承载能力和承载强度系数的概念,为定量分析城市轨道交通系统能力的变化和能力的输出提供了科学依据。在借鉴以往线路承载能力计算方法的基础上,结合TOC理论及分布估计算法,建立了城市轨道交通网络系统设计承载能力计算模型,并对上海轨道交通网络系统进行实例研究,验证了该计算模型的可行性和有效性。城市轨道交通网络系统设计承载能力问题的研究是一个探索性强、内容丰富、涉及因素较为复杂的课题,本文虽然比较系统地探讨了其概念、影响因素和计算方法,且取得一定的研究成果,但重点围绕换乘站因素对系统设计承载能力的影响而展开,而对其他与运输服务质量相关的一些约束条件,例如列车运行过程中的平均速度、列车的异质性、时刻表的稳定性以及系统网络效应等因素未进行深入研究。因此,在以后的研究中,应进一步深入研究其他因素对系统设计承载能力的影响,使计算模型更贴近实际,应用范围更广。
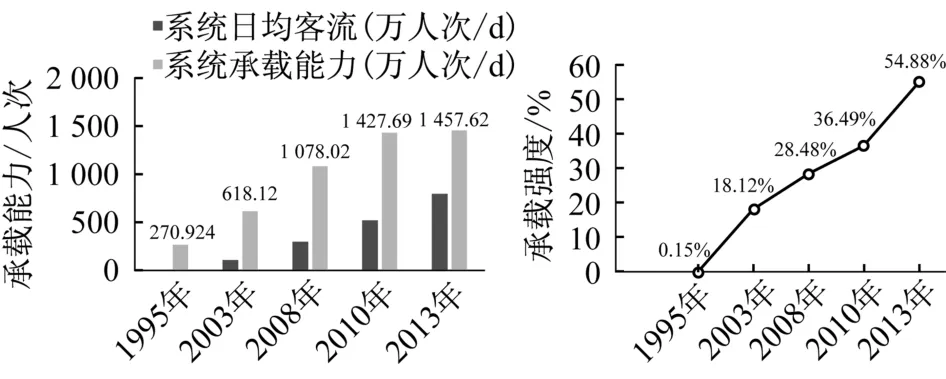
图3 上海市轨道交通网络系统设计承载能力变化趋势
参考文献
[1] 张一梅.基于路网的城市轨道交通系统运输能力研究[D].北京:北京交通大学,2009.
[2] 杨维.城市轨道交通路网承载能力计算方法研究[D].北京:北京交通大学,2011.
[3] 皇妍妍.基于网络的城市轨道交通运输能力瓶颈问题研究[D].北京:北京交通大学,2011.
[4] 汪波,韩宝明,战明辉,等.城市轨道交通运输能力计算及加强研究[J].城市轨道交通研究,2013(4):38.
[5] 候德劭,晏克非,柳伍生.基于遗传算法的停车约束下城市路网承载能力分析模型[J].计算机应用,2008,28(4):1074.
[6] 李俊芳.基于运输能力的城市轨道交通运输能力方案评价研究[D].成都:西南交通大学,2007.
[7] 付婷.城市轨道交通车站集散能力瓶颈识别[D].北京:北京交通大学,2014.
[8] 周树德,孙增圻.分布估计算法综述[J].自动化学报,2007,33 (2):113.
Calculation of the Designed Loading Capacity in Urban Rail Transit Network System
Li Xiaolong,Han Jingru,Song Liuyang
AbstractBy intergrading the definition and characters of the designed loading capacity(DLC)of urban rail transit network system,the factors influencing DLC are overall studied.Based on the past calculation methods,the theory of constraint is used to calculate DLC of each line.Considering the formation characteristics of the system,a calculation model is built based on the estimation of distribution algorithms,which is applied to calculate DLC of urban rail transit netweok system.Finally,Shanghai rail transit network system is taken as an example to test the calculation model.The result proves that this model has smaller amount of calculation,faster speed and better practicability, and can effectively reflect the current status of Shanghai rail transit.
Key wordsurban rail transit netsystem;loading capacity; theory of constraint;estimation of distribution algorithms; calculation model
(收稿日期:2015-04-08)
DOI:10.16037/j.1007-869x.2016.02.014
中图分类号U 293.6

