高架轨道轮轨噪声预测分析∗
曾钦娥雷晓燕
(1.北京市劳动保护科学研究所,100054,北京; 2.华东交通大学铁路环境振动与噪声教育部工程研究中心,330013,南昌∥第一作者,助理研究员)
高架轨道轮轨噪声预测分析∗
曾钦娥1雷晓燕2
(1.北京市劳动保护科学研究所,100054,北京; 2.华东交通大学铁路环境振动与噪声教育部工程研究中心,330013,南昌∥第一作者,助理研究员)
摘 要随着我国城市轨道交通的快速发展,高架轨道作为一种经济、实用、安全、快速的交通模式,在城市轨道交通建设中得到越来越广泛的运用,但由此带来的振动噪声对周围环境的影响也变得十分突出。通过建立轮轨噪声预测模型,运用有限元法分析箱型梁、U型梁阻抗,对高架轨道轮轨噪声进行预测分析。讨论了桥梁截面型式、行车速度、轨道扣件刚度、桥梁结构阻尼、桥梁支座刚度对高架轨道轮轨噪声的影响。分析结果表明,行车速度和扣件刚度对轮轨噪声有较大影响,在200 Hz以下,轮轨噪声总体上随着扣件刚度的增大而增大;在200~800 Hz范围内,轮轨噪声随着扣件刚度的增大反而减小;在800 Hz以上,扣件刚度对轮轨噪声无明显影响。桥梁截面型式仅在低频部分对轮轨噪声有较大影响,而桥梁结构阻尼、桥梁支座刚度则对高架轨道轮轨噪声影响甚微。
关键词高架轨道;轮轨噪声;噪声预测;参数分析
∗国家自然科学基金项目(U1134107);江西普通高校科技落地计划项目(KJLD11002)
First author′s address Beijing Municipal Institute of Labour Protection,100054,Beijing,China
随着我国城市轨道交通的迅速发展,出于对路基工后沉降控制、地基条件、节约土地、工程造价、环境保护等多种因素的考虑,高速铁路和城市轨道大多采用“以桥代路”的策略,因此高架轨道所占的比例越来越大。与路面线路相比,列车驶经高架线路时道路两侧噪声级增加2~20 dBA[1]。由于高架轨道交通大多穿越或位于闹市区和居民区,轮轨噪声、车辆噪声及桥梁结构产生的铁路振动噪声对周围环境的影响变得十分突出。轮轨噪声是铁路噪声的主要噪声源[2-3],因此有必要对高架轨道轮轨噪声进行理论分析。
1 高架轨道轮轨噪声预测模型
轮轨表面不平顺[4]是产生轮轨振动和噪声的直接原因,定义为车轮(或钢轨)实际表面相对于理想运行基面的局部幅度。当车轮在钢轨不平顺表面上滚动时,会冲击钢轨,结果使得轨道与列车间产生受迫振动,向外辐射出声波而产生噪声,称为轮轨噪声。预测高架轨道的轮轨噪声,需将轮轨不平顺作为激励输入,首先分析轮轨系统的振动响应,再根据振动对轮轨噪声进行预测。图1为高架轨道轮轨噪声预测示意图。
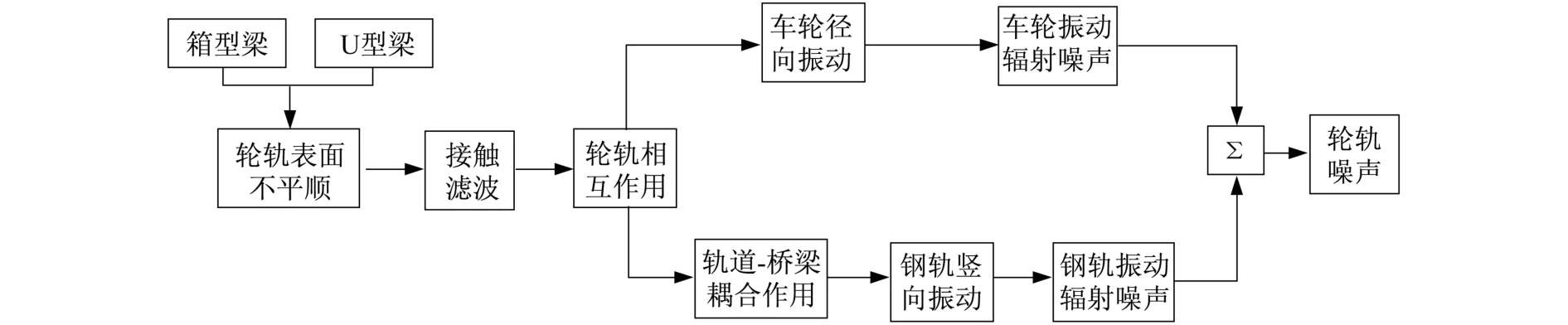
图1 高架轨道轮轨噪声预测示意图
根据图1,建立轮轨噪声预测模型。模型中把钢轨假设为以列车速度v运动着的有限长线声源,车轮则假设为点声源[5],即辐射的声波在自由场中以球面波传播,为单极子球面声源。不考虑地面反射的影响,则车轮轴数为N速度为v的列车通过时,高架轨道轮轨噪声总声压级谱
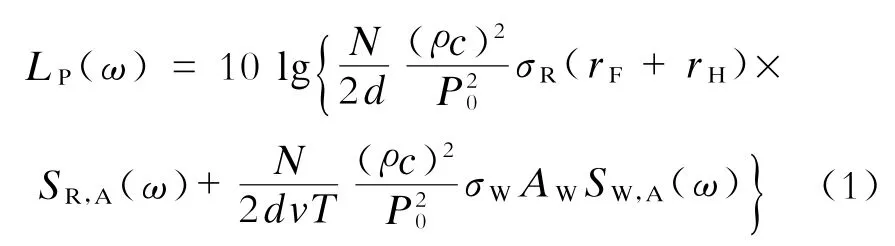
式中:
d——噪声观察点到钢轨的垂直距离;
rF——钢轨底部宽度;
rH——钢轨头部宽度;
σR——钢轨竖向振动辐射效率;
SR,A(ω)——高架轨道钢轨竖向振动平均功率谱,其中ω为圆频率;
P0——标准参考声压,为2×10-5Pa;
AW——车轮径向辐射面积;
σW——车轮径向辐射效率;
SW,A(ω)——车轮径向振动的平均功率谱,采用有限元法计算得到;
T——列车通过时间;
ρ——空气的密度;
c——空气中的声速。
2 高架轨道钢轨竖向振动平均功率谱的计算
2.1高架轨道阻抗计算
利用有限元软件ANSYS建立轨道-箱梁耦合系统模型。为了能较好地预测高架轨道结构的振动特性,建立有限元模型时,将钢轨视为Euler梁,采用Beam188梁单元进行模拟,钢轨扣件和桥梁支座采用线性弹簧-阻尼单元(Combin14)模拟;道床结构和桥梁均采用实体单元(Soild45)模拟,采用映射网格划分将其划分为六面体单元,由于本文忽略桥墩对轨道结构振动的影响,因此采用固定约束模拟桥墩。梁体、轨道板均采用实际尺寸;钢轨采用60 kg/m钢轨,弹性模量为206 GPa,密度为7 830 kg/m3;扣件间距为0.625 m,扣件刚度为60 MN/m;轨道板为钢筋混凝土结构,弹性模量为39 GPa,密度为2 500 kg/m3;高架桥梁采用长度为32 m的箱梁结构,弹性模量为36.2 GPa,密度为2 500 kg/m3;桥梁支座为橡胶支座,刚度为3.38×109N/m。
为分析高架桥结构对轨道振动特性的影响,本文分别建立了不同桥梁截面形式的轨道-桥梁振动有限元分析模型,对轨道-箱型梁和轨道-U型梁的有限元模型进行网格划分,如图2所示。荷载作用点位于桥梁跨中左股钢轨处,响应点取激励点作用处,计算高架轨道原点速度阻抗,如图3所示。
2.2钢轨接触点速度功率谱
根据“输出谱=|传递函数|2×输入谱”这一基本关系式,以轮轨表面不平顺谱作为输入谱,并引入滤波函数|H(k)|2,得到钢轨在荷载接触点处的竖向振动速度功率谱值
2.2 PVT1在肝癌中的表达与临床特征关系 PVT1在肝癌中的表达水平与肝癌患者肿瘤大小、肿瘤数量、BCLC分期、血管侵犯、甲胎蛋白的表达水平相关(P<0.05);与肝癌患者性别、年龄、饮酒史、吸烟史、HBsAg表达、肝硬化、Child-Pugh分级、癌胚抗原、谷丙转氨酶和谷草转氨酶表达水平无关(P>0.05)。
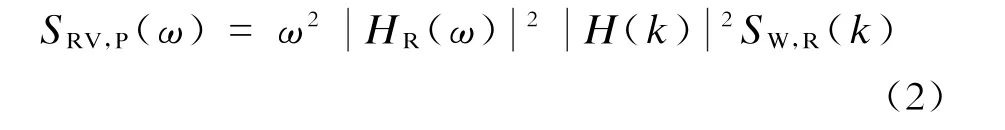
式中:
H(k)——滤波器传递函数;
SW,R(k)——轮轨联合粗糙度的波数谱。
HR(ω)——振动传递函数,其表达式为:
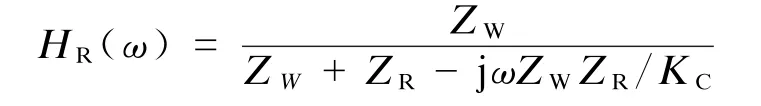
式中:
ZW——车轮径向速度原点阻抗;
ZR——钢轨径向速度原点阻抗;
KC——接触弹簧刚度。

图2 高架轨道有限元模型
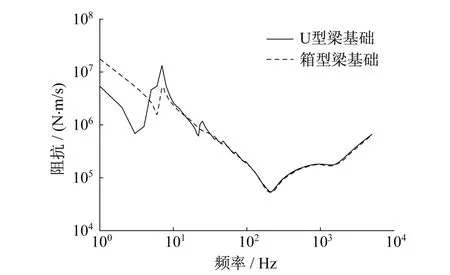
图3 高架轨道速度阻抗
2.3钢轨振动平均速度功率谱
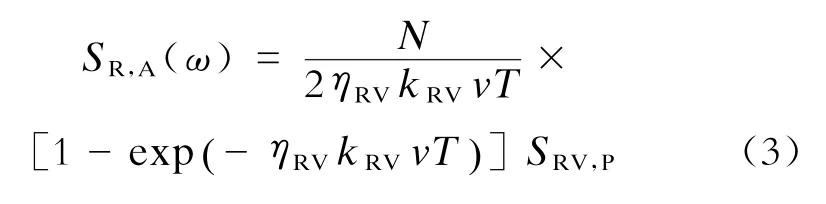
式中:
ηRV——轨道振动衰减系数;
N——列车的轮对数;
kRV——钢轨振动弯曲波数;
v——列车运行速度;
SRV,P——接触点速度功率谱。
3 高架轨道轮轨噪声预测分析
根据前面所建立的模型对高架轨道轮轨噪声进行预测,测量点距轨道垂直距离为7.6 m,距离地面高度为1.9 m,v=80 km/h,列车通过时间T=8 s。计算结果如图4所示。
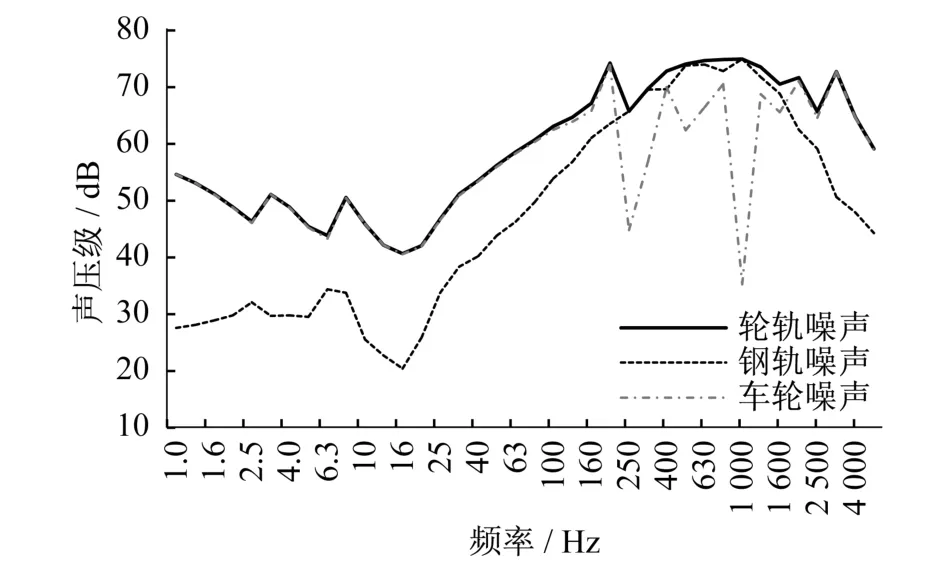
图4 高架轨道轮轨噪声声压级谱
从图4可以得出,在中心频率为200 Hz以下及2 000 Hz以上车轮噪声起主导作用,在3 150 Hz处出现峰值;中心频率在200~2 000 Hz范围内钢轨噪声起主要作用,在此范围内,轮轨噪声达到最大值。在全频范围内,车轮噪声出现了较多的峰值,在1 000 Hz出现了最低值,这主要是由于有较多的自振频率,而且在1 000 Hz处车轮的振动最小。
4 高架轨道轮轨噪声影响参数
4.1不同截面形状高架轨道轮轨噪声计算
对两种桥梁截面形状的高架轨道轮轨噪声进行预测,考虑到U型截面梁两侧的腹板具有阻隔噪声的作用,对U型截面梁高架轨道轮轨噪声的预测必须在腹板内,因此测量点距离轨道垂直距离取1 m。预测结果如图5所示,从图5可以看出,截面形状对高架轨道的轮轨噪声的影响主要集中在40 Hz以下。在40 Hz以上,两种桥梁截面形状的高架轨道轮轨噪声无明显区别。
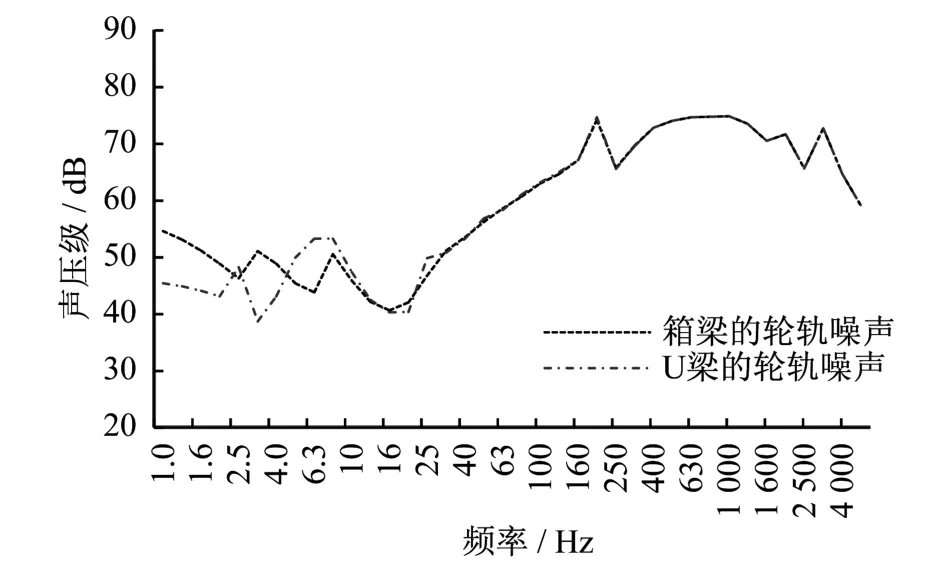
图5 不同桥梁截面形状高架轨道轮轨噪声
4.2行车速度对高架轨道轮轨噪声影响
为分析高架轨道轮轨噪声的速度特性,对不同速度高架轨道轮轨噪声的1/3倍频程进行计算,车辆运行速度分别取60 km/h、80 km/h、120 km/h、160 km/h、200 km/h,计算结果如图6所示。
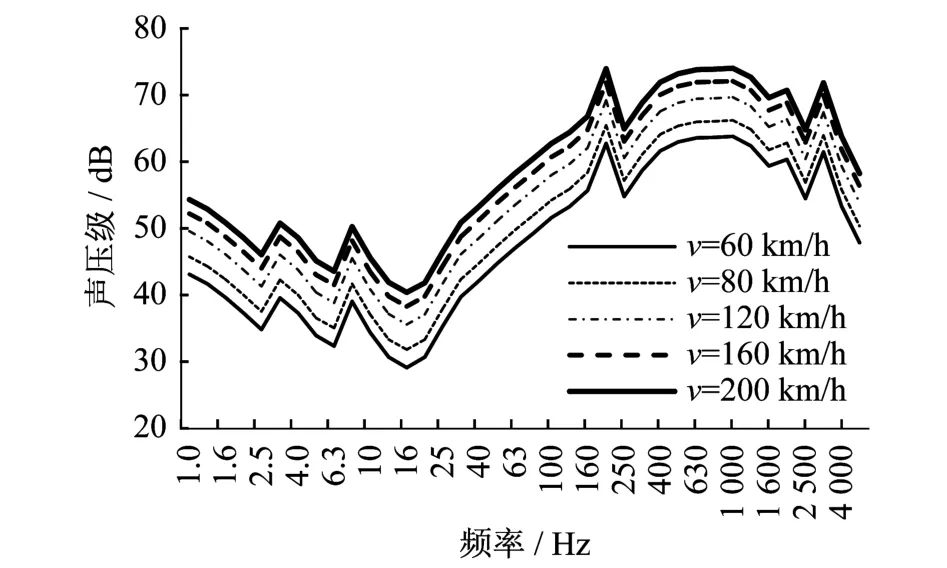
图6 不同速度下轮轨噪声声压级谱
从图6可以看出,随着列车运行速度的增大,各个频率的轮轨噪声相应增大,而且各速度轮轨噪声的趋势一致,没有出现明显的区别。另外,随着列车运行速度的增大,各频率的轮轨噪声增加的幅度趋缓。由图6可知,当列车速度从80 km/h增加到120 km/h时,各频率范围内的轮轨噪声约增大3.5 d B;当列车速度从120 km/h增加到160 km/h时,各频率范围内的轮轨噪声约增大2 d B;当列车速度从160 km/h增加到200 km/h时,各个频率范围内的轮轨噪声约增大1.5 dB。
4.3扣件刚度对高架轨道轮轨噪声的影响
为分析扣件刚度(k r)对高架轨道轮轨噪声的影响,k r分别取30 MN/m、60 MN/m、100 MN/m、200 MN/m时的计算结果如图7所示。从图7中可以看出,在200 Hz以下,轮轨噪声总体上随着扣件刚度的增大而增大,这主要是车轮相应的频带声压级谱的影响结果;而在200~800 Hz范围内,刚度增大,则轮轨噪声减小,该频段内钢轨辐射噪声占主导地位,扣件刚度的变化直接影响钢轨的振动。在800 Hz以上,四种扣件刚度条件下的曲线基本重合,说明扣件刚度对轮轨噪声无明显影响。
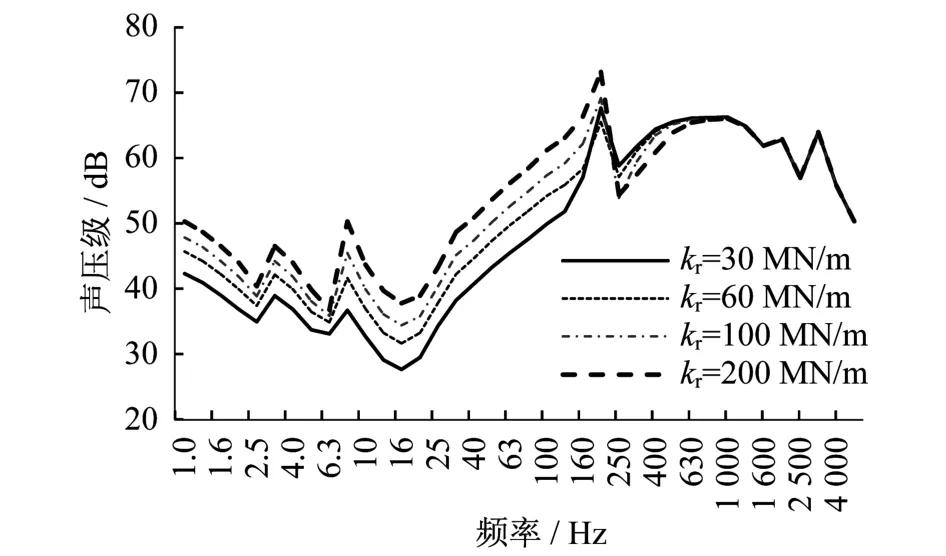
图7 不同扣件刚度下轮轨噪声声压级谱
4.4桥梁结构阻尼对高架轨道轮轨噪声的影响
为分析桥梁结构阻尼对轮轨噪声的影响,ξ分别取0.01、0.03、0.05时的计算结果如图8所示。
从图8可以得出,在160~2 000 Hz范围内,随着桥梁结构阻尼的增大,轮轨噪声反而减小,该频段内主要为钢轨辐射噪声,说明桥梁结构阻尼对高架轨道的振动产生较大影响。在2.5 Hz和6.3 Hz两个谷值处,随着桥梁结构阻尼的增大,轮轨噪声也增大,此时主要为车轮辐射噪声,说明此时桥梁结构阻尼对轮轨之间的传递函数影响较大。在其他频率内,桥梁结构阻尼对高架轨道的轮轨噪声基本无影响。
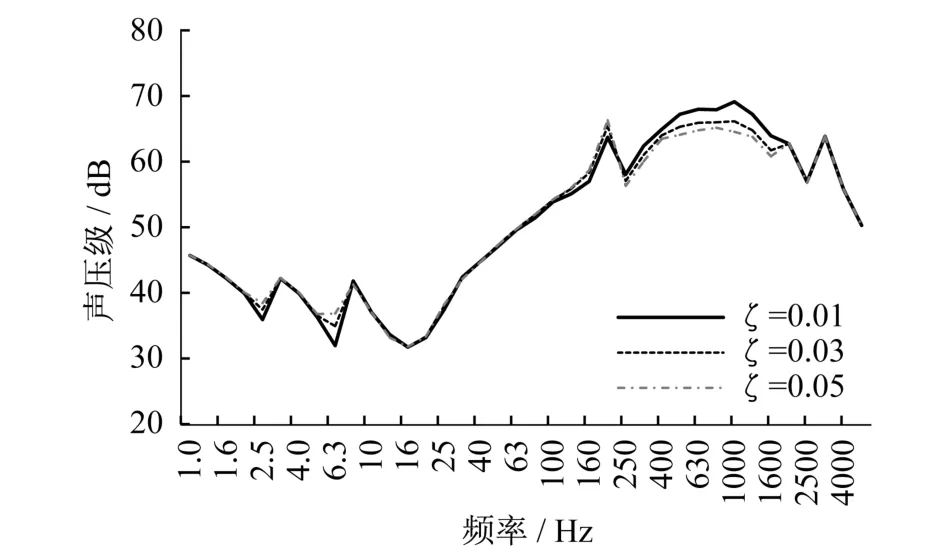
图8 不同桥梁结构阻尼下的高架轨道轮轨噪声
4.5桥梁支座刚度对高架轨道轮轨噪声影响
取三个不同的桥梁支座刚度k1,k2、k3分别为
3.38×109N/m、2×3.38×109N/m、5×3.38×109N/m,分析桥梁支座刚度变化对轮轨噪声的影响,计算结果如图9所示。从图9可以看出,一定范围内桥梁支座刚度的变化对高架轨道轮轨噪声无影响。
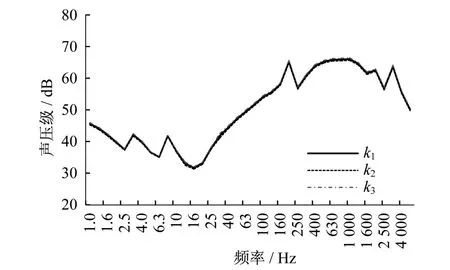
图9 不同桥梁支座刚度下轮轨噪声声压级谱
5 结论
(1)对于高架轨道结构的轮轨噪声,中心频率在250 Hz以上及2 000 Hz以下范围内,车轮噪声起主导作用,在3 150 Hz处出现峰值;在2 500~2 000 Hz,钢轨噪声占主导地位。其中车轮噪声出现了较多的峰值,在1 000 Hz出现了最低值,这主要是由于在1 000 Hz处车轮的导纳值最小。
(2)随着列车运行速度的增大,各个频率的轮轨噪声相应增大。且随着列车运行速度的增大,各频率轮轨噪声的增加幅度逐渐趋缓。
(3)钢轨扣件刚度对轮轨噪声的影响主要分布在中心频率为800 Hz以下,表现为影响轨道的振动以及轮轨之间的耦合作用,减小扣件刚度有利于降低轮轨噪声。
(4)在8 Hz以下,随着桥梁结构阻尼的增大,轮轨噪声也增大;在160~2 000 Hz范围内,随着桥梁结构阻尼的增大,轮轨噪声反而减小,而在其他频率范围内,桥梁结构阻尼对轮轨噪声无明显影响。
(5)桥梁支座刚度对高架轨道轮轨噪声影响甚微。
参考文献
[1] Kurzwcil L G.Prediction and control of noise from railway bridges and tracked transit elevated structures[J].Journal of Sound and Vibration,1977,51(3):419.
[2] 焦大化.铁路环境噪声控制[M].北京,中国铁道出版社, 1990:50.
[3] 雷晓燕,圣小珍.铁路交通噪声与振动[M].北京:中国铁道出版社,2004.
[4] 陈向东.轮轨振动、噪声模型及预测[D].大连:大连交通大学,2004.
[5] 刘林芽,雷晓燕.练松良.铁路轮轨噪声预测分析[J].噪声与振动控制.2008(4):73.
[6] 雷晓燕,圣小珍.现代铁路轨道理论研究[M].北京:中国铁道出版社,2006:321.
[7] Remington P J.Wheel/railing noise,II:Validation of the theory[J].Journal of Sound and Vibration,1987,81 (6):1825.
Analysis of Elevated Rail Wheel/Rail Noise Prediction
Zeng Qin’e,Lei Xiaoyan
AbstractWith the rapid development of urban rail transit in China,elevated rail as an economic,practical,safe and rapid transport mode,has been used widely in urban transport.But at the same time,the influence of vibration and noise caused by elevated rail over the environment becomes very prominent.In this paper,the finite element method is used to establish the prediction model of wheel/rail noise, and to analyze the impedance of box beam and U beam and predicte the wheel/rail noise.The influence of bridge cross-section type,vehicle speed,track fastener stiffness, bridge structural damping,and bridge bearing stiffness over the wheel-rail noise on elevated rail is discussed.The analysis results show that,the driving speed and fastener stiffness have greater influence over the wheel/rail noise, which is below 200 Hz,and the increase of fastener stiffness will directly raise the wheel/rail noise.But in the range of 200~800 Hz,the increase of fastener stiffness will reduce the wheel-rail noise;while above 800 Hz,fastener stiffness will have no obvious effect on wheel/rail noise.The cross-section type bridge has a greater influence over the wheel/rail noise in part of the frequency,but the structural damping and support stiffness of a bridge only have less effect over the wheel/rail noise.
Key wordselevated track;wheel/rail noise;noise prediction;parameter analysis
(收稿日期:2014-03-28)
DOI:10.16037/j.1007-869x.2016.02.003
中图分类号U 491.9+1∶U 233

