基于同心圆环的大间距子阵级阵列栅瓣抑制

李志刚 王鹏毅

(中国电子科技集团公司第五十四研究所,石家庄 050081)

基于同心圆环的大间距子阵级阵列栅瓣抑制

李志刚 王鹏毅

(中国电子科技集团公司第五十四研究所,石家庄 050081)

适当增加单元间距和应用子阵级阵列有利于降低相控阵的设计成本,但是阵列的稀疏会带来不期望的栅瓣．为解决该问题,设计了一种无栅瓣阵列:子阵在平面内旋转,围绕阵列中心呈同心圆环分布．为保证子阵之间不会交叠,对圆环半径范围进行了分析．利用一种改进的穷举算法,对每一层圆环上的子阵个数以及圆环半径进行了计算机仿真优化．结果表明,以4×4子阵共1 024个单元为例,所提方法可抑制峰值旁瓣电平约-17.48 dB．

栅瓣抑制;大间距;子阵旋转;同心圆环阵;稀疏阵

引 言

如何降低相控阵天线的设计成本一直是一个热门话题,为此可以从两方面考虑: ①在阵列孔径尺寸一定条件下，合理减少单元数量,拉开单元间距,可减小互耦获得高增益,但是会带来栅瓣[1];②子阵级波束形成,与单元级波束形成相比子阵级波束形成极大地减小了通道数,降低了硬件成本和工程实现的难度[2].

在大间距阵列中,每一个子阵都有自己的栅瓣,整个阵列的栅瓣抑制可以通过以下几种方法进行抑制:

1) 自适应波束形成[3]．该方法运用自适应加权使子阵方向图在高旁瓣位置形成凹陷,但是需要实时调整单元权值,增加了计算负担,甚至数据与权值有可能会失匹配．

2) 虚拟阵列[4]．该方法通过内插虚拟天线实现小间距组阵来抑制栅瓣,然而计算复杂度会随之增加,且原来白噪声也会受到污染变成色噪声,波束形成性能受到影响．

3) 非规则子阵．采用多种子阵,不同子阵单元间距不同[5],或者单元间距相同、子阵规模不同[6]．该方法虽然可以抑制栅瓣,但是并不利于子阵的统一生产及降低制造成本．

4) 子阵间距优化[7-9]．采用同一子阵,对子阵中心位置进行优化．子阵个数越多优化的自由度越大[8],但计算复杂度会随之成倍增加,并且子阵位置分布的规则性也会降低．

本文基于同一子阵,给出了一种具有对称结构的无栅瓣布阵方法:子阵围绕阵列中心等间距地呈同心圆环分布；然后设计了子阵的各项参数,并分析了圆环半径的取值范围；最后为最小化峰值旁瓣电平(Peak Side-lobe Level, PSL),对每层圆环的子阵个数和圆环半径进行了仿真优化．

1 阵列布局

单元间距大于半波长时，阵列的方向图会有栅瓣．不妨设单元间距d=λ,λ为波长，图1显示的是d=λ方形栅格阵列的方向图．从图1中可以看出,栅瓣增益与主瓣增益一样高．

图1 方形栅格阵列方向图(d=λ)

文献[8]提出把阵列分成Ns个相同的矩形栅格子阵,通过调整子阵位置,能够达到最小栅瓣电平，可以由式(1)估计：

δ=-10lgNsdB,

(1)

子阵个数越多,公式(1)估计越精确．文献[9]对104个方形栅格子阵进行平移优化,可抑制栅瓣-16.5dB,与公式(1)的理论值20.17dB还差约3.7dB．

除子阵平移外,子阵旋转[8]可以分散栅瓣的能量,对栅瓣起到抑制效果．但是子阵无规律的旋转可能会导致子阵之间重叠,因此子阵平移位置和旋转角度都需要进行合理设计及优化．本文对子阵进行平面旋转,并将子阵围绕阵列中心呈同心圆环分布[10],效果如图2所示．为便于阵列上下(左右)形成差波束,阵列分别关于X轴和Y轴对称．

图2 阵列布局效果示意图 (1 024个单元分为64个子阵)

2 方向图函数

子阵为Ne×Ne方形栅格结构,单元的水平和垂直间距均为d,那么子阵的边长为L=Ned,单元的位置(xm,ym)可以求出．设各单元等幅激励,子阵的方向图可以表示为[11]

(2)

式中:k=2π/λ，

(3)

表示观察方向的方向余弦;u0和v0表示扫描方向的方向余弦;与阵面垂直方向俯仰角度φ为0°．

把子阵等间距地放置于同心圆环上,并围绕阵列中心进行平面旋转．阵列共有Ns个子阵被放置在Nr个同心圆环上,设第n(n=0,1,…,Nr)环上子阵的个数为Nn,圆环半径为rn．特别的,n=0表示阵列的中心．那么第n环第m个子阵的中心坐标为

(xn,m,yn,m)=rn(cosαn,m,sinαn,m)

(4)

式中:αn,m=2π(m-1)/Nn+αn,0为子阵的旋转角度,如图2所示,αn,0为附加在第n环上的一个可以调节的旋转角度．

把子阵看成一个单元,整个阵列的方向图可以用子阵级方向图表示为[11]

(5)

式中,Fn,m(u,v)表示第n环第m个子阵的方向图,子阵方向图可以通过对子阵旋转和平移后求出,旋转矩阵为

(6)

需要说明的是:

1) 对于线极化天线,若子阵不一致,旋转阵列的波束形成会极为不方便;若子阵一致,不同子阵的极化平面可能会不同．

2) 对于圆极化天线,如果子阵被旋转了,辐射波的相位会变化相同的角度．通过标准的校准技术进行阵列校准,子阵旋转引起极化的幅相变化可以得到补偿[8]．为便于分析,本文假设天线为理想的圆极化天线．

3 子阵位置优化

3.1 基本思路

影响方向图函数的主要参数包括:子阵内参数,如单元间距d、子阵大小Ne×Ne、子阵个数Ns等;子阵间参数,如圆环上子阵个数Nn、圆环个数Nr、圆环半径rn以及圆环的旋转角度αn,0等．上述每一个参数的变化都会导致阵列方向图的改变,需要优化的参数众多,计算量庞大．我们优化阵列分布的基本思路是:固定子阵内的参数,优化子阵间的参数,使得峰值旁瓣电平达到最小．需要注意的是,在优化过程中还有一个限制条件,即子阵之间不能发生重叠．

3.2 子阵参数设计

3.3 子阵旋转角度设计

圆环旋转角度αn,0的设置．为了保持阵列的对称结构,αn,0可以为0或者π/Nn．如果αn,0均设为0或者π/Nn,落在对称轴上的子阵等效于只进行了平移,而没有进行旋转．子阵旋转的目的就是为了把栅瓣能量打散．为了减少等效平移子阵的数量,可以让某一层圆环的旋转角度为0,让相邻的另一层圆环的旋转角度为π/Nn,依法交替设置αn,0．

3.4 圆环半径范围

上述参数设定后,在一定孔径范围内对圆环半径进行调节,以寻找最小的PSL．在调节过程中,子阵不应存在交叠,从而每一层圆环的半径存在上边界和下边界．

对于最外层圆环,可以预先设定半径的上边界为一常数B;对于非最外层圆环,半径rn的最大值受到外一层圆环半径的限制,第n环子阵的外切圆半径应小于第n+1环子阵的内切圆半径,利用勾股定理有

(7)

化简公式(7),得到rn的上边界Bu(rn)为

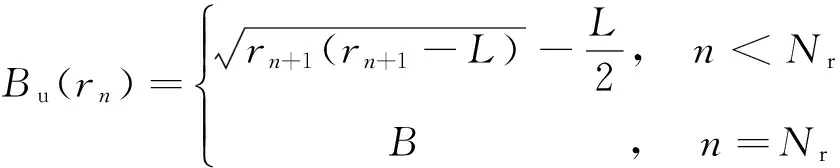
(8)

当第n环的半径rn减小到最小时,子阵的边角紧紧相邻,子阵朝向阵列中心的边共同组成一个正多边形,边数为Nn．可以计算出该正多边形内切圆半径,再加上子阵边长的一半,即得出rn的下边界Bl(n)为

(9)

3.5 优化算法

下面优化子阵间参数:圆环半径rn和每层圆环上子阵个数Nn．

1) 优化流程

针对阵列最佳分布综合法的研究提出了很多种,如穷举法、遗传算法、模拟退火法等[12]．遗传算法和模拟退火法容易陷入局部最优解,穷举法可得到最优解,但是计算量庞大、难以实现．

本文对穷举法进行了改进,对参数rn和Nn分别进行遍历,流程如图3所示.

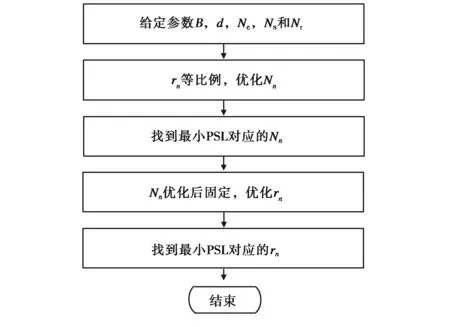
图3 一种改进的穷举优化策略流程

步骤如下:

① 确定最外层圆环半径B,固定子阵内参数,包括:单元间距d、子阵大小Ne×Ne、子阵个数Ns,固定圆环个数Nr;

② 暂时等比例设定rn,优化圆环上子阵个数Nn,为保持阵列轴对称性,Nn设为偶数,Nn的步进长度为dΔ1=2,每次步进计算当前阵列的PSL;

③ 步骤② 循环结束后,寻找最小PSL对应的Nn;

④ 固定Nn,遍历半径rn,步长不妨设为dΔ2=λ/20,每次步进计算当前阵列的PSL;

⑤ 步骤④循环结束后,寻找最小PSL对应的rn,优化过程结束．

2) 运算量分析

(10)

如果采用穷举法,rn和Nn联合遍历的次数由阵列孔径的大小、子阵个数及层数共同决定．所提优化过程把rn和Nn的联合遍历分解成了两个独立的一维遍历过程．

表1给出了一种运算量的示例．

表1 运算量示例(B=22λ,Ns=64,Nr=4)

每次计算PSL的时间由u,v的分辨率设置和计算机运行速度决定,可采用多核处理器并行计算．由表1看出,穷举法对rn和Nn联合遍历,计算量庞大,往往难以实现;所提方法的计算量是两维优化各自计算量的加和,以一种可行的计算量得到一组次优解．

4 仿真结果与分析

为得到最小的PSL,以MATLAB为仿真平台,对圆环上的子阵个数Nn和圆环半径rn进行了优化,其他的参数设置如表2所示．

表2 参数设置

首先,64个子阵分布在4层同心圆环上,圆环半径rn暂时等比例固定,对每一层圆环上子阵的个数Nn进行优化,优化结果为分别4、12、20和28．对Nn优化后的方向图如图4所示,PSL为-14.54 dB．

图4 rn等比例,对Nn优化后的方向图

然后,每一层圆环上子阵的个数Nn固定后,对圆环半径rn进行优化,经优化后结果分别为4.6λ、9.55λ、15.25λ和22λ．最终,优化结果如表3所示．

表3 1 024单元圆环半径和圆环上

图5显示了rn和Nn优化后阵列未扫描时的方向图．尽管单元之间的最小间距为d=λ,然而由图4可以看出阵列并不存在栅瓣,PSL的最小值可以达到-17.48 dB,与公式(1)的理论估计结果-18.06 dB相差0.58 dB．

图6是扫描角度为60°时的方向图．由图6看出： 当波束指向扫描时,PSL为-15.85 dB,与没有扫描时相比,PSL抬高了1.63 dB．

图5 rn和Nn优化后阵列的方向图(未扫描时)

图6 rn和Nn优化后阵列的方向图(扫描60°时)

图7 全方位扫描时归一化峰值旁瓣电平的分布情况

文献[9]把1 664个单元分成104个方形栅格子阵进行平移优化,未扫描和扫描10°时,方位向旁瓣电平均低于-16.5 dB．为了与文献[9]进行对比,本文也采用相同的单元个数和子阵个数进行布阵,布阵优化结果如表4和图8所示．由图8看出,扫描10°时PSL可以达到-19.64 dB,优于文献[9]的结果3.14 dB,与公式(1)的理论值相差约0.5 dB．

表4 参数优化结果(1 664个单元分为104个子阵)

图8 1 664单元优化后方向图(扫描10°时)

5 结 论

针对大间距、子阵级的无栅瓣布阵问题,给出了一种基于同心圆环的布阵方法,并对布阵参数进行了仿真优化．结果表明,以1 024单元为例,本文对包括栅瓣在内的旁瓣电平抑制结果与理论值相差约0.58 dB,且所设计的阵列呈轴对称分布,易于形成差波束,为低成本、高增益相控阵天线的工程实现提供了一种理论参考．

[1] MAILOUX R J. Phased array antenna handbook [M]. Boston: Artech Hause, 2005: 80.

[2] KRIVOSHEEV Y V, SHISHLOV A V. Grating lobe suppression in phased arrays composed of identical or similar subarrays [C]//IEEE International Symposium on Phased Array Systems and Technology. Waltham, MA, USA, Oct. 2010: 724-730.

[3] 程乃平, 潘点飞. 大型阵列天线子阵划分及栅瓣抑制方法[J]. 信号处理, 2014, 30(5): 535-543.

CHENG N P, PAN D F. Subarray partition method and grating lobe suppression for large array anenna [J]. Journal of signal processing, 2014, 30(5): 535-543. (in Chinese)

[4] 汪月清, 刘姜玲, 王小谟, 等. 虚拟阵元应用于平板端射天线的新型组阵方法研究[J]. 电波科学学报, 2014, 29(4): 663-667.

WANG Y Q, LIU J L, WANG X M, et al. Method of making up virtual plate end-fire antenna array [J]. Chinese jounal of radio science, 2014, 29(4): 663-667. (in Chinese)

[5] 朱瑞平, 王朝阳. 一种低栅瓣大瞬时带宽相控阵天线的设计方法[J]. 电波科学学报, 2008, 23(4): 745-748.

ZHU R P, WANG C Y. Design method for wide band and low grating lobe phased array antennas [J]. Chinese jounal of radio science, 2008, 23(4): 745-748. (in Chinese)

[6] REN Y L, WANG J, LUO T G. Research on grating lobe reduction in limited scan phased array antenna [C]//Cross Strait Quad-Regional Radio Science and Wireless Technology Conference. Chengdu, China, 2013: 230-233.

[7] TOYAMA N. Aperiodic array consisting of subarrays for use in small mobile earth stations [J]. IEEE transactions on antennas and propagation, 2005, 53(6): 2004-2010.

[8] KRIVOSHEEV Y V, SHISHLOV A V, DENISENKO V V. Grating lobe suppression in aperiodic phased array antennas composed of periodic subarrays with large element spacing [J]. IEEE antennas and propagation magazine, 2015, 57(1): 76-85.

[9] 罗天光, 王建, 任永丽, 等. 采用DFP-BFGS优化大间距子阵级非周期八角阵[J]. 现代雷达, 2014, 36(3): 62-69.

LUO T G, WANG J, REN Y L, et al. An octagonal aperiodic array antenna optimizing large spacing’s subarray using DFP-BFGS algorithm [J]. Modern radar, 2014, 36(3): 62-69. (in Chinese)

[10] HAUPT R L. Optimized element spacing for low sidelobe concentric ring arrays [J]. IEEE transactions on antennas and propagation, 2008, 56(1): 266-268.

[11] 张光义. 相控阵雷达系统[M]. 北京: 国防工业出版社, 1994: 96-97.

[12] 刘恒, 刘波, 谢广钱, 等. 迭代傅里叶算法用于六边形稀疏阵列天线[J].电波科学学报, 2015, 30(6): 1235-1240.

LIU H, LIU B, XIE G Q, et al. Iterative Fourier technique applied for Hexagon thinned array [J]. Chinese journal of radio science, 2015, 30(6): 1235-1240. (in Chinese).

Grating lobe suppression in large spacing arrays composed of subarrays based on concentric ring

LI Zhigang WANG Pengyi

(The54thResearchInstituteofCETC,Shijiazhuang050081,China)

Increasing element spacing appropriately and using subarray-based arrays are favorable to reduce the production cost of phased arrays, however, the rarefied array has unexpected grating lobes. To solve the proplems, an array is designed with no grating lobe. The subarrays are rotated in plane, and are distributed in the concentric ring structure around the center of the array. The range of the ring radii are analyzed for ensuring that each subarray will not overlap. Computational simulation is carried out to optimize the number of the subarrays in each ring and the radii of the ring using an improved method of exhaustion. The results show that, taking 4×4 subarrays and 1 024 elements as example, the method provides suppression of peak side-lobe level of -17.46dB.

grating lobe suppression; large spacing; subarray rotation; concentric ring arrays; sparse arrays

10.13443/j.cjors.2016010101

2016-01-01

中国电子科技集团公司第五十四研究所发展基金(XX151060006)

TN957.2

A

1005-0388(2016)06-1132-06

李志刚 (1982-),男,河南人,博士,中国电子科技集团第五十四研究所高级工程师，主要研究方向为航天测控、阵列天线技术．

李志刚,王鹏毅. 基于同心圆环的大间距子阵级阵列栅瓣抑制[J]. 电波科学学报,2016,31(6):1132-1137.

LI Z G, WANG P Y. Grating lobe suppression in large spacing arrays composed of subarrays based on concentric ring[J]. Chinese journal of radio science,2016,31(6):1132-1137. (in Chinese). DOI: 10.13443/j.cjors.2016010101

联系人： 李志刚 E-mail: lizhigang0372@126.com

DOI 10.13443/j.cjors.2016010101