基于最小二乘的同步多用户非周期长码直扩信号扩频序列估计

张天骐 强幸子 马宝泽 王俊霞

(重庆邮电大学 信号与信息处理重庆市重点实验室,重庆 400065)

基于最小二乘的同步多用户非周期长码直扩信号扩频序列估计

张天骐 强幸子 马宝泽 王俊霞

(重庆邮电大学 信号与信息处理重庆市重点实验室,重庆 400065)

针对低信噪比下同步多用户非周期长码直扩信号的扩频序列估计问题,提出了一种基于嵌套迭代最小二乘投影算法的扩频序列估计方法. 首先,将同步多用户非周期长码直扩信号等效为含有缺失数据的相应的短码直扩信号. 然后,利用最大似然估计理论对相应的短码直扩信号进行数学分析,构建扩频序列估计的数学模型. 最后,利用一种嵌套迭代最小二乘投影算法来实现扩频序列的估计. 研究表明,该算法在低信噪比(小于-10 dB)情况下,对多用户(多达10路)扩频序列的估计有着良好的性能表现.

长码直扩信号;缺失数据模型;最大似然估计;嵌套迭代最小二乘投影算法

引 言

直接序列扩频(DirectSequenceSpreadSpectrum,DSSS) 信号由于其抗干扰能力强、保密性能好、直扩通信速率高以及便于实现多址通信等优点,在军事和民用通信系统中得到广泛应用,如超长波对潜通信及第三代移动通信CDMA系统等. 在合作通信系统中,合作接收方可利用已知的扩频码序列对接收到的直接序列扩频信号进行解扩提取信息码. 然而在非合作通信系统中,特别是在低信噪比条件下,需要事先对扩频序列进行估计才能完成信号的盲解扩. 因此,扩频序列估计已成为目前研究的热点之一.

在非合作直扩通信系统中,针对多用户短码直扩信号(扩频周期等于信息码周期)扩频序列估计的相关文献较多,较为成熟. 目前已有方法大致可分为:基于奇异值分解的方法[1-3]、基于最大似然估计的方法[4-5]、基于子空间的方法[6]、基于模式识别聚类的方法[7-8]、基于盲源分离的方法[9]以及基于神经网络的方法[10]等. 对于相应周期长码直扩信号扩频序列估计的相关工作大多是对短码直扩信号估计方法的扩展. 但是针对多用户非周期长码直扩信号扩频序列估计的相关研究较少[11]. 文献[12]提出一种基于平行因子的长码直扩信号扩频序列盲估计方法,但该方法需要多通道接收技术来保证阶维矩阵低秩分解的唯一性. 文献[13]通过构造缺失数据模型,利用奇异值分解(SingularValueDecomposition,SVD)算法对扩频序列进行估计,该方法实际是利用迭代过程首先估计出与长码直扩信号对应的短码直扩信号,然后利用SVD得到扩频序列子空间的估计值,再将缺失数据矩阵投影到扩频序列子空间,通过期望最大化(ExpectationMaximization,EM)算法对扩频序列进行估计. 当用户数较多,且噪声污染比较严重时,该方法运算复杂度明显增强,且估计效果不理想.

本文的核心思想是利用文献[13]的思路,将同步多用户非周期长码直扩信号建模为含有缺失数据的相应短码直扩信号,利用最大似然估计理论对信号模型进行分析,并提出一种嵌套迭代最小二乘投影算法实现各用户扩频序列的估计.

1 同步多用户DSSS模型

定义1 设A,B分别为两个m×n矩阵,A=(aij)m×n,B=(bij)m×n. 记

A⊙B=(aijbij)m×n,

(1)

称A⊙B为A与B的hadamard乘积矩阵.

实际非合作场景中,K路用户长码直扩接收信号模型可写为

n=0,1,…,N-1.

(2)

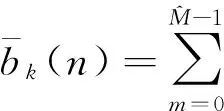
针对同步多用户长码直扩信号,满足τ1=τ2=…=τk=τ. 在实际情况中,式(2)中各个用户载波的初始相位φk往往是不同的,但考虑到文献[14]可对各个用户的载波相位进行估计,然后将其等效为异步多用户长码直扩信号模型. 对于异步多用户长码直扩信号模型,将另作文章具体分析,本文假设f1=f2=…=fk=f及φ1=φ2=…=φk=φ.

假设信号已经过盲同步处理,即τ=0. 此时,基带同步多用户长码直扩信号可写为

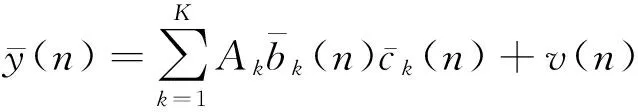
n=0,1,…,N-1.

(3)

信号样本的列向量形式为

(4)

同时将信息码、扩频码序列以及噪声序列写成矩阵形式:

(5)

(6)

(7)

为方便起见,将各用户的信号幅度乘入扩频序列矩阵中,如式(6)所示. 此时,式(2)可以写为如下形式:

(8)

式中,Z为K个1组成的列向量. 式(8)结构如图1所示.

图1 同步多用户长码DSSS信号模型

本文假设用户数已知,且每个用户中扩频序列的长度、信息码元的宽度均已事先被估计[2,15]出来.

现在用含有缺失数据的同步多用户短码直扩信号虚拟同步多用户长码直扩信号模型. 虚拟一个与该多用户长码直扩信号扩频码序列和信息码序列相同对应的短码直扩信号,则该短码直扩信号加噪并离散化后可写为

(9)

(10)

式中:

(11)

V表示噪声矩阵.

Y的结构如图2所示.

图2 虚拟多用户短码直扩信号模型

图3 缺失数据模型

2 扩频序列估计

2.1 最大似然理论分析

(12)

其负对数最大似然函数为

(13)

依据最大似然估计原理,当式(13)取最小值时对应的C和B为该最大似然函数所对应的最大似然概率估计. 由于式(13)中K和σ均为常数项,上述最大似然估计问题可以转化为如下最小二乘估计问题.

2.2 最小二乘估计方法

根据最大似然函数的表达式,可以将以上问题建模为

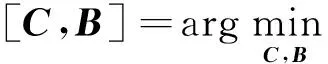
(14)

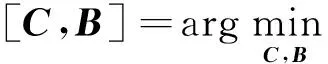
(15)

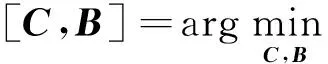
(16)

得到B2,依此迭代,直到B收敛(Bn=Bn+1). 当固定B时,C的求解过程与上述方法类似.

综上所述,对于目标函数式(15)的求解方法实际上是采用了一种嵌套迭代最小二乘投影算法进行求解[16-17]. 具体步骤如下:

2)n=n+1,j=0,k=0.

3)j=j+1,

(17)

6)k=k+1;

(18)

本文所提算法主体是采用最小二乘方法,因此其计算复杂度主要集中在对缺失数据矩阵求伪逆,而求伪逆的计算复杂度又主要由乘法构成,对一个X×Y的矩阵求伪逆,共需要XY2+2Y3次乘法,因此算法步骤3)中迭代过程的计算复杂度为iLM2+2iM3,步骤5)中迭代过程的计算复杂度为jLM2+2jM3,总体的计算复杂度为n(i+j)LM2+2n(i+j)M3,其中i,j,n分别表示步骤3)、步骤5)和整体的迭代次数. 文献[13]首先利用SVD对扩频序列子空间进行估计,然后再利用EM算法对扩频序列进行估计,SVD估计扩频序列子空间的算法复杂度约为(L+M)3; EM算法复杂度主要集中在对矩阵求逆,复杂度约为nLM2+2nM3; 总体算法复杂度为(2n+1)M3+(n+3)LM2+3L2M+L3. 因此,本文算法与文献[13]算法的计算复杂度从数量级上来说是相当的,并且扩频码序列的长度对本文算法计算复杂度影响较小.

2.3 收敛性

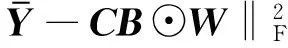
2.3.1 步骤3)迭代过程中的收敛性证明

(19)

(20)

(21)

(22)

(23)

由于

(24)

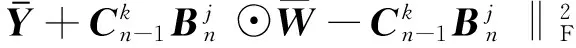
(25)

(26)

(27)

2.3.2 步骤6迭代过程中的收敛性证明

(28)

(29)

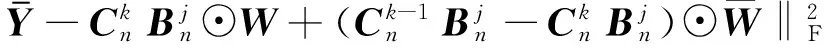
(30)

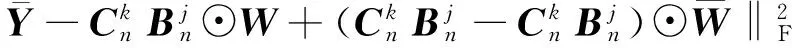
(31)

(32)

由于

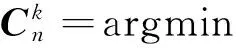
(33)

(34)

(35)

(36)

2.3.3 整体迭代过程中的收敛性证明

假设在步骤3中迭代结束后目标函数为

(37)

在步骤6中迭代结束后目标函数为

(38)

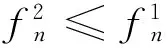
(39)

取得最小值,又因为

(40)

(41)

(42)

当且仅当Cn=Cn-1,Bn=Bn-1时,等号成立.因此,该算法在整体迭代的过程中也是收敛的.

2.4 可辨识性

为论证本文算法迭代过程中收敛结果的确定性,这里提出可辨识性[16]的定义以及两个性质,性质证明详见附录A.

性质1 对于YL×N=CL×KBK×N,如若C和B满足以下条件,则Y的K维分解可辨识.

1)C和B分别为列满秩和行满秩矩阵;

2)B中的任一元素Bi,j∈{+1,-1};

3)B中存在着这样的2K-1列:在这2K-1列中既没有完全相同的列,也没有完全相反的列.

性质2 对于YL×N=(CL×KBK×N)⊙WL×N,W(n)L+1,[n/G]+1=1,其中,(n)L表示n除L取余数,n=0,1,…,GN-1. 如若C和B满足以下条件,则Y的K维分解可辨识.

1)C和B分别为列满秩和行满秩矩阵;

2)B中的任一元素Bi,j∈{+1,-1};

3)B中存在着这样的2K-1列:在这2K-1列中既没有完全相同的列,也没有完全相反的列.

4)C中任意连续的G行所组成的子矩阵均为列满秩矩阵.

5) 2G-a-1>K,其中a=GCD(G,L),GCD表示最大公约数.

3 仿真实验

下面用计算机仿真的方法对本文算法的性能进行分析.不失一般性,仿真中扩频及信息码序列采用随机产生的双相移相键控(Binary Phase Shift Keying, BPSK)调制序列,算法收敛判别中参数设置为ρ1=10-4,ρ2=10-4,ρ=10-2. 采用误码率作为该算法性能评价指标. 误码率计算公式为

(43)

式中:nm表示第m次蒙特卡洛仿真中估计错误的扩频序列的个数;K为用户数;L为扩频序列长度;M为蒙特卡洛仿真次数. 信噪比计算公式为

(44)

实验一 验证本文算法的可行性,取L=63,G=30,固定信号样本长度(取信息码个数为3 000的数据段). 在信噪比为-7dB的情况下,对K=5的多用户长码直扩信号扩频序列进行估计. 首先,将信号样本按照第2节中缺失数据模型的构造过程构造成缺失数据矩阵,然后利用3.2节中算法步骤进行迭代运算,直至满足收敛条件,得到各个用户扩频序列的估计值. 计算仿真实验结果如图4(a)和(b)所示.

(a) 扩频序列真实值

(b) 扩频序列估计值图4 不同用户的扩频序列真实值和估计值

对比图4(a)和(b)可知,本文算法在信噪比为-7dB的情况能够准确地估计出多路用户所对应的扩频序列.

实验二 验证本算法在不同用户数下的性能,固定信号样本长度(取信息码个数为3 000的数据段). 在K=7,8,9,10时,信噪比在-15～0dB时,分别在L=127,G=50和L=1 023,G=500的条件下估计所得扩频序列的误码率,蒙特卡洛仿真200次后所得性能曲线如图5(a)和(b)所示.

(a) L=127,G=50

(b) L=1 023,G=500图5 不同L和G条件下时误码率曲线

由图5可知:当信噪比为-10dB时,该算法能够在L=1 023,G=500时对10路用户的扩频序列进行有效分离; 且在其他条件给定时,随着用户数的减少,性能增强; 扩频周期越长,本文算法的抗噪性能越强.

实验三 验证信息码长度对算法性能的影响. 取L=1 023,G=500,RSN=-10dB. 分别在K=8,9,10,信息码个数为500～4 000时,估计所得扩频序列的误码率,蒙特卡洛仿真200次后所得性能曲线如图6所示.

图6 数据组数对扩频序列估计的影响

由图6可知:随着信息码长度的增加,算法估计性能不断提高; 相同条件下,用户数越少,算法估计性能越好.

实验四 验证本文算法在不同用户数下的收敛

速度,固定信号样本长度(信息码个数为3 000的数据段),取RSN=-10dB时,在L=1 023,G=500.当K=6,8,10时,本文算法在迭代过程中扩频序列误码率的变化情况如图7所示.

图7 收敛速度曲线

由图7可知:本文算法能够通过迭代运算不断降低扩频序列估计值的误码率,直到收敛; 用户数越多,所需的迭代次数越多,收敛速度越慢.

实验五 固定信号样本长度(取信息码个数为3 000的数据段). 在L=1 023,G=500,K=6的条件下,通过200轮蒙特卡洛仿真对照本文算法与文献[13]在不同信噪比(-15～0dB)条件下扩频序列估计误码率的变化曲线,仿真结果如图8所示.

由图8可知,本文算法在整体上优于文献[13]算法. 信噪比越低,本文算法相对于文献[13]算法的优势越明显,说明本文算法的抗噪性能较文献[13]算法要好.

图8 不同信噪比条件下扩频序列估计性能对照

4 结 论

本文针对同步多用户非周期长码直扩信号扩频序列估计问题,提出了一种基于嵌套迭代最小二乘投影算法的扩频序列估计方法,并对该方法的收敛性进行了较为详细的理论推导,研究表明:本文算法在信噪比低于-10dB时可对L=1 023,G=500的多达10路用户的同步多用户非周期长码直扩信号扩频序列实现准确估计. 本文方法可应用于卫星通信以及电子对抗中扩频序列估计,特别是多用户非周期长码信号扩频序列的估计.

附录A

性质1证明:假设存在C′、B′同样是Y的分解矩阵,并且C′、B′也满足如上条件. 则有

Y=CB=C′B′.

(A1)

由于B′是行满秩矩阵,可得

C′=CB(B′)†.

(A2)

式中,(B′)†表示B′的伪逆. 若对两边同时乘以B′,则有

CB=C′B′=CB(B′)†B′,

(A3)

即

C[B-B(B′)†B′]=0.

(A4)

因为C是列满秩矩阵,故必有.

B=B(B′)†B.

(A5)

(A5)又因为B和B′均为行满秩矩阵,所以B(B′)†是一个非奇异的方阵,令T=B(B′)†,即有

B=TB′.

(A6)

(A7)

(A8)

方程(A7)的解为:t11和t12中一个为±1,一个为0. 方程(A8)的解与(A7)类似. 结合T为非奇异矩阵,则T满足:每一行中只有一个±1,其它为0,T可逆. 此时,TB′实际上只是对B′进行了行交换,即Y是可辨识的.

假设K=k时,Y是可辨识的. 此时,T满足:任意一行中只有一个±1,其它为0,且T可逆.

现在考虑K=k+1时,

(A9)

按照性质中所给条件,不失一般性的假设

(A10)

按照式(A6)展开第一行即有

(A11)

因为方程组中如若除去第一列,后边k列的排列组合总是成对出现(总有与之完全相反的项出现),根据K=2时的结论,该方程的解应为

(A12)

或者

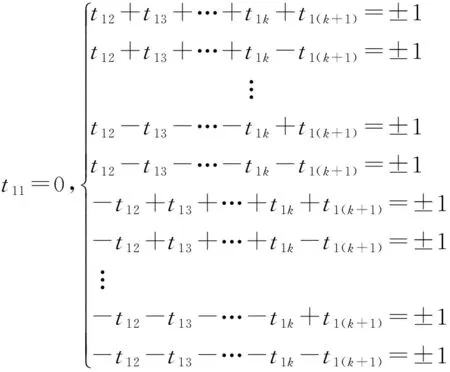
(A13)

对于第一种解的情况,显然后边方程组的解各项都为0; 对于第二种解的情况,后边方程组的上半部分是对应K=k时的情况,根据K=k时的假设,方程组的解只能是:存在一个±1的解,其它为0. 综上所述,对于式(A6)在K=k+1的情况下,T的第一行的解只能是:存在一个±1,其它项为0.

同理可证,其它各行的解的形式与第一行相同. 同时,由于T可逆,所以T矩阵是一个单纯的行交换矩阵,即Y可辨识.

综合以上归纳证明可知,当YL×N=CL×KBK×N,C和B满足性质中所给的三个条件时,Y是可辨识的.

性质2证明:令

(A14)

令

(A15)

[1] 张天骐, 张传武, 林孝康. 直扩信号伪码周期及序列的估计算法[J]. 系统工程与电子技术, 2005, 27(8): 1365-1368.

ZHANGTQ,ZHANGCW,LINXK.AlgorithmsforperiodandsequenceestimationofthePNcodeinDS-SSsignals[J].Systemsengineeringandelectronics, 2005, 27(8): 1365-1368.(inChinese)

[2] 张天骐, 周正中, 林孝康,等. 低信噪比长伪码直扩信号的盲估计方法[J]. 信号处理, 2008, 24(3):370-376.

ZHANGTQ,ZHOUZZ,LINXK,etal.ApproachtoblindestimationoflowerSNRlongcodeDSsignals[J].Signalprocessing, 2008, 24(3):370-376.(inChinese)

[3] 沈斌, 王建新. 基于奇异值分解的直扩信号伪码序列及信息序列盲估计方法[J]. 电子与信息学报, 2014, 36(9): 2098-2103.

SHENB,WANGJX.BlindestimationofthePNsequenceandinformationsequenceofaDSSSsignalbasedonSVD[J].Journalofelectronics&informationtechnology, 2014, 36(9): 2098-2103.(inChinese)

[4]ZHANGHG,MOUQ,LHS.AsemidefiniterelaxationapproachtospreadingsequenceestimationforDS-SSsignals[J].IEICEtransactionsoncommunications, 2011,E94-B(11): 3163-3167.

[5] 周德强, 陈卫东. 基于Viterbi算法的扩频码与信息序列联合估计[J]. 飞行器测控学报, 2014, 33(5): 441-447.

ZHOUDQ,CHENWD.JointblindestimationofspreadingcodeandinformationsequencebasedonViterbialgorithm[J].JournalofspacecraftTT&Ctechnology, 2014, 33(5): 441-447.(inChinese)

[6] 马超, 张立民, 王建雄. 基于子空间跟踪的长码直扩序列盲估计[J]. 计算机与数字工程, 2014,292(42): 223-226.

MAC,ZHANGLM,WANGJX.BlindestimationoflongcodeDSSSsignalbasedonsubspacetracking[J].Computer&digitalengineering, 2014,292(42): 223-226.(inChinese)

[7]CHENGH,LOUZH,SUNGL.Non-supervisedrulefordirectsequencespreadspectrumsignalsequenceacquisition[C]//2014NinthInternationalConferenceonBroadbandandWirelessComputing,CommunicationandApplications(BWCCA).IEEE,November8-10, 2014:151-154.

[8] 李军伟, 张天骐, 朱洪波,等. 基于聚类的多进制扩频伪码序列盲估计方法[J]. 科学技术与工程, 2014, 14(2): 32-36.

LIJW,ZHANGTQ,ZHUHB,etal.ClusteringbasedblindestimationofPNsequencesinmaryspreadspectrumsystem[J].Sciencetechnologyandengineering, 2014, 14(2): 32-36.(inChinese)

[9] 汤辉. 直扩信号参数估计的盲源分离方法研究[D]. [D]. 武汉: 华中科技大学, 2012.

TANGH.ParametersestimationofDSSSsignalsbasedonblindsourceseparation[D].Wuhan:HuazhongUniversityofScience&Technology, 2012. (inChinese)

[10] 张天骐, 林孝康, 周正中. 基于神经网络的低信噪比直扩信号扩频码的盲估计方法[J]. 电路与系统学报, 2007, 12(2): 118-123.

ZHANGTQ,LINXK,ZHOUZZ.Aneuralnetworkapproachtoblind-estimationofPNspreadingsequenceinlowerSNRDS/SSsignals[J].Journalofcircuitsandsystems, 2007, 12(2): 118-123.(inChinese)

[11] 赵知劲, 顾骁炜, 沈雷，等. 非周期长码直扩信号的伪随机码盲估计[J]. 通信学报, 2015,36(5): 1-8.

ZHAOZJ,GUXW,SHENL,etal.Blindestimationofpseudo-randomcodesinnon-periodiclongcodedirect-sequencespread-spectrumsignals[J].Journaloncommunications, 2015,36(5): 1-8.(inChinese)

[12] 赵知劲, 李淼, 吴金沂. 长码直扩信号扩频序列估计[J]. 杭州电子科技大学学报, 2015, 35(2): 1-4.

ZHAOZJ,LIM,WUJY.Thespreadspectrumcodeestimationoflong-codeDSSSsignal[J].JournalofHangzhouDianziUniversity(NaturalSciences), 2015, 35(2): 1-4.(inChinese)

[13] 张花国, 魏平. 同步多用户长码直扩信号的盲解扩[J]. 电子与信息学报, 2011,33(7): 1748-1751.

ZHANGHG,WEIP.Blinddespreadingofsynchronousmulti-userlong-codeDS-SSsignals[J].Journalofelectronics&informationtechnology, 2011,33(7): 1748-1751.(inChinese)

[14] 张花国, 魏平. 未知频偏下直扩信号的扩频序列估计[J]. 电子科技大学学报, 2013, 42(1): 44-47.

ZHANGHG,WEIP.Spreadingsequenceestimationofdirectsequencespreadspectrumsignalswithunknowncarrieroffset[J].JournalofUniversityofElectronicScienceandTechnologyofChina, 2013, 42(1): 44-47.(inChinese)

[15] 徐海源, 王丰华, 黄知涛，等. 长码直扩信号的符号速率盲估计方法[J]. 国防科技大学学报, 2007, 29(6): 44-48.

XUHY,WANGFH,HUANGZT,etal.BlindestimationoftheSymbolrateofalongcodeDSSSsignal[J].JournalofNationalUniversityofDefenseTechnology, 2007, 29(6): 44-48.(inChinese)

[16]TALWARS,VIBERGM,PAULRAJA.Blindseparationofsynchronousco-channeldigitalsignalsusinganantennaarray.I.algorithms[J].IEEEtransactionsonsignalprocessing, 1996, 44(5): 1184-1197

[17]TALWARS,PAULRAJA.Blindseparationofsynchronousco-channeldigitalsignalsusinganantennaarray.II.Performanceanalysis[J].IEEEtransactionsonsignalprocessing, 1997, 45(3): 706-718.

Estimation of the spread spectrum sequence for synchronous multi-user aperiodic long-code DSSS signals based on least squares

ZHANG Tianqi QIANG Xingzi MA Baoze WANG Junxia

(ChongqingKeyLaboratoryofSignalandInformationProcessing,ChongqingUniversityofPostsandTelecommunications,Chongqing400065,China)

This paper studies the problem of estimation of the spread-spectrum sequence for low SNR synchronous multi-user long-code direct sequence spread spectrum (DSSS) signals. An estimation approach of spread-spectrum sequence based on a nested iterative least squares with projection (NILSP) algorithm is presented. First, The synchronous multi-user long-code DSSS signals is constructed as the short-code ones with missing data. Then the mathematical analysis for the short-code ones with missing data is done based on the theory of maximum likelihood estimation (MLE) to establish a mathematical model of spread-spectrum sequence. After that, the spread-spectrum sequence is estimated by a NILSP algorithm. The theoretical analysis and simulations show that, the proposed algorithm always has a good performance for estimation of multi-users’ (more than 10 users) spread-spectrum sequence in low-SNR (lower than -10 dB) scenarios, and under the same conditions, the longer the data size, the better the performance.

long-code direct sequence spread spectrum (DSSS) signals; missing data model; maximum likelihood estimation(MLE); nested iterative least squares with projection (NILSP)

10.13443/j.cjors.2016030201

2016-03-02

国家自然科学基金(61671095，61371164，61275099)；信号与信息处理重庆市市级重点实验室建设项目(CSTC2009CA2003)；重庆市教育委员会科研项目(KJ130524，KJ1600427，KJ1600429)

TN911

A

1005-0388(2016)06-1113-11

张天骐 (1971-),男,四川人,重庆邮电大学教授,博士,研究方向为扩频信号的盲处理、神经网络实现以及信号的同步处理.

强幸子 (1986-),男,陕西人,重庆邮电大学硕士研究生,研究方向为直扩信号盲处理.

马宝泽 (1990-),男,河北人,重庆邮电大学硕士研究生,研究方向为通信信号盲源分离.

王俊霞 (1990-),女,河南人,重庆邮电大学硕士研究生,研究方向为通信信道编码.

张天骐,强幸子,马宝泽, 等. 基于最小二乘的同步多用户非周期长码直扩信号扩频序列估计[J]. 电波科学学报,2016,31(6):1113-1123.

ZHANG T Q, QIANG X Z, MA B Z,et al. Estimation of the spread spectrum sequence for synchronous multi-user aperiodic long-code DSSS signals based on least squares [J]. Chinese journal of radio science,2016,31(6):1113-1123.(in Chinese). DOI:10.13443/j.cjors.2016030201

联系人： 张天骐 E-mail: zhangtq@cqupt.edu.cn

DOI 10.13443/j.cjors.2016030201