大气扰动对深空通信天线组阵性能的影响

朱庆林 孙方 王红光 田耀佳 刘琨 张利军

(中国电波传播研究所,青岛 266107)

大气扰动对深空通信天线组阵性能的影响

朱庆林 孙方 王红光 田耀佳 刘琨 张利军

(中国电波传播研究所,青岛 266107)

大气结构常数;大气扰动;对流层延迟;精密单点定位;深空通信;天线组阵;相位误差

引 言

随着深空甚长基线干涉测量(Very Long Baseline Interferometry, VLBI)探测技术的发展,深空任务中向更远行星探测的需求越来越迫切,任务要求传输的探测数据量也越来越大,用于深空探测的频段已从S、X频段全面升级到Ka频段[1]．与此同时,远距离、高频段的系统指标导致信号传输路径损失极大,这就要求地面站采用大口径抛物面天线,尽量增加接收面积以提高信噪比,然而天线口径越大/波束越窄,探测器下行信号的捕获越难．美国航空航天局(National Aeronautics and Space Administration, NASA)深空网的70 m口径大天线已达目前的工程极限,要进行深空更远距离的探测必须采用天线组阵技术．天线组阵是指在一定地域范围内多个天线组成阵列,将各天线接收到的同一信源的信号合成,提高接收信噪比[2]．在各天线噪声不相关的条件下,理论上N个天线组阵接收信号的信噪比是单个天线的N倍．若用体积小、重量轻、波束宽的中小口径天线组阵,则对信号捕获跟踪更为有利．另外,在能力扩展、可靠性、灵活性、多目标通信和成本等方面,天线组阵比单个大天线的优势更加明显[3]．

组阵信号的合成主要考虑信号相位,而影响信号相位的最显著因素是地球对流层底部大气扰动导致的水蒸汽波动．通过长期的测量误差源统计分析,NASA等科研机构普遍认为:由扰动造成的大气随机噪声将会成为VLBI深空测控通信系统中最大的相位误差源之一．表1给出了美国NASA深空网天线阵在Ka频段的相位误差精度分配指标[4-6].

表1 NASA测控站误差源精度分配指标

1 PPP解算对流层天顶延迟

20世纪70年代初,Anderle利用卫星多普勒观测值确定单站的位置,首次引入PPP的概念．随着几十年的技术发展,90年代GNSS国际地球动力学服务局(International GNSS Service,IGS)成立,并向全球播发高精度的精密卫星轨道和钟差产品,此后还发展成等级不同的事后、快速和预报三种星历以及相应的精密卫星钟差产品,为精密单点定位提供了解决思路．随后,美国喷气推进实验室(Jet Propulsion Laboratory,JPL)的研究人员Zumberge等提出利用IGS提供的精密星历,同时用一个GPS跟踪站网的数据确定5 s间隔的卫星钟差,基于单点定位方程估计出对流层参数、接收机钟差和测站坐标的精密单点定位研究思路,确定了利用非差相位观测值进行精密单点定位的可行性．

传统的精密单点定位一般通过GPS实现,近十几年来,随着我国北斗导航卫星系统BDS工作突飞猛进的发展与逐步完善,也使其具备了PPP技术实现的可能．IGS产品中的对流层天顶延迟是基于JPL开发的GIPSY软件的解算结果,其被公认为目前精度最高的GNSS单点定位软件之一．田耀佳、朱庆林[9-12]等人利用自研模型软件进行了基于北斗系统的天顶延迟解算．图1给出了分别利用BDS和GPS系统解算的西沙站天顶延迟随时间的变化．

图1 西沙站基于BDS和GPS解算的天顶延迟

由图1可以看出,基于北斗系统的精密单点定位方法估计的天顶延迟精度与基于GPS系统的解算精度相当,整体趋势基本保持一致,大小也基本在同一范围内．BDS的建立将会为整个亚洲太平洋地区提供更大量的观测值,确保对现有的GNSS气象学有重大的推进．

GNSS信号穿过大气层进入地面,经过了整个的对流层,“携带”了大量的对流层信息,因此GNSS精密单点定位除了可以进行精确定位之外,还能用于探测对流层信息,其方法是利用非差观测方程,将对流层延迟看作未知数进行求解:

(1)

式中:P和φ分别为码伪距和相伪距观测值;ρ为卫星至接收机的几何距离;c为真空中的光速; dt为接收机钟差; dT为卫星钟差;Ttrop为对流层延迟;Tiono为电离层延迟;Tmult为多路径延迟;εP和εφ分别为码观测值和相位观测值的测量噪声;N为卫星和接收机之间的整周模糊度;λ为载波信号波长．图2给出了PPP估计对流层天顶延迟的工作流程．

图2 PPP估计对流层天顶延迟框图

2 大气结构常数估计

发生扰动时,我们可以将大气折射率写成以下形式:

由表4可知，第一次浮选精煤平均灰分14.70%，精矿加清水稀释后再浮选，浮选精煤灰分降低到8.68%，最终精煤产率34.54%。二次浮选工艺可燃体回收率57.26%，煤泥在二次浮选工艺下的可浮性为难浮。考虑到工业生产时一次浮选精矿的稀释水为循环水，以及高灰细泥的影响，一般情况下，二次浮选精煤灰分比一次浮选精煤灰分低2%～3%，可达10.5%左右。

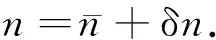
(2)

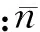
(3)

根据经典的Kolmogorov-Obukhov“2/3”扰动理论和随机场理论,用来描述不同位置ri、rj上的空间大气折射的结构函数定义为[8]

Dn(δr) =〈[δn(ri)-δn(rj)]2〉

(4)

n(z',t0+t)]2〉+〈[n(z,t0+t)-

n(z',t0)]2〉-〈[n(z,t0)-

n(z',t0)]2〉-〈[n(z,t0+t)-

z')2+v2t2]1/3-|z-

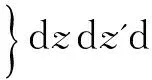
(5)

式中:t0代表统计平均的起始时刻;τ为统计时间段;H为扰动大气的有效高度,一般取H=2 km．

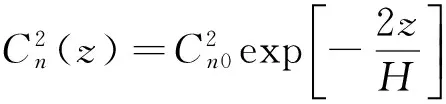
(6)

3 大气随机相位误差

在大气扰动作用下,深空天线阵元间的大气相位差φatm是随机变量,会直接导致天线阵实际的合成增益低于理想值．根据天线阵元间干涉相位结构函数与大气结构常数之间的关系,与时间相关的相位结构函数可以写成[13]

=〈|ΔS(t)-ΔS(t+Δt)|2〉．

(7)

(8)

式中:v‖为平行于基线的平均风速;k为波数;H为扰动层的有效特性高度,一般取2 km;β为Kolmogorov能量定律常数,一般取5/3．则对流层大气随机相位误差的统计平均值可以用下式计算:

(9)

式中:d为基线距离;

(10)

(11)

(12)

式中:T为特性时间,可由干涉仪基线距离与水平风速求解; Γ为伽马函数．随着深空通信频率的升高,大气随机相位误差的起伏程度会成倍增加,使得在恶劣大气环境下工作的天线组阵通信性能很不稳定．以NASA深空网的X频段为例,恶劣环境下的大气随机相位误差可达近50°,引入的合成增益损失将高达3 dB[14-16]．图3给出了天线阵合成增益损失与扰动大气造成的相位误差关系曲线,这里误差指均方根误差．

图3 天线阵合成增益损失与相位误差关系曲线

4 计算结果分析

IGS产品中的对流层天顶延迟是基于JPL开发的GIPSY软件的解算结果,其被公认为目前精度最高的GNSS单点定位软件之一．图4～7中的大气天顶延迟利用项目组自主研发的软件生成．自研软件与IGS提供的GIPSY软件解算的对流层产品之间的偏差、标准偏差及均方根误差均在毫米量级,解算精度与GIPSY解算对流层的精度相当．自研软件采用的是IGS发布的事后15 min间隔的精密轨道产品和30 s间隔的精密钟差产品．

表2给出利用图4～7中的大气延迟标准偏差统计估算出的不同深空站在典型月份中一天内的大气结构常数值．

图4 北京24 h内大气延迟变化量

图5 上海24 h内大气延迟变化量

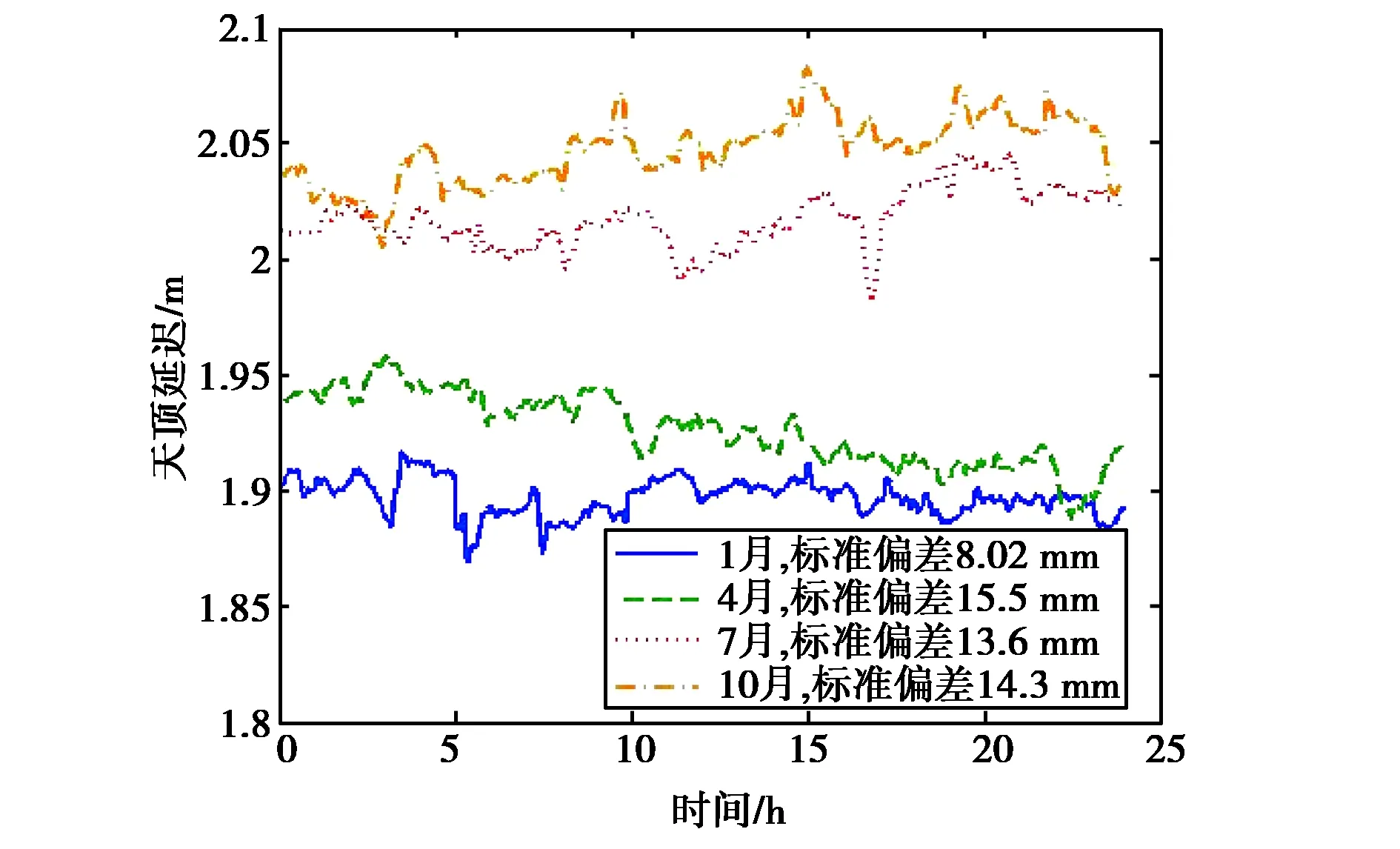
图6 昆明24 h内大气延迟变化量

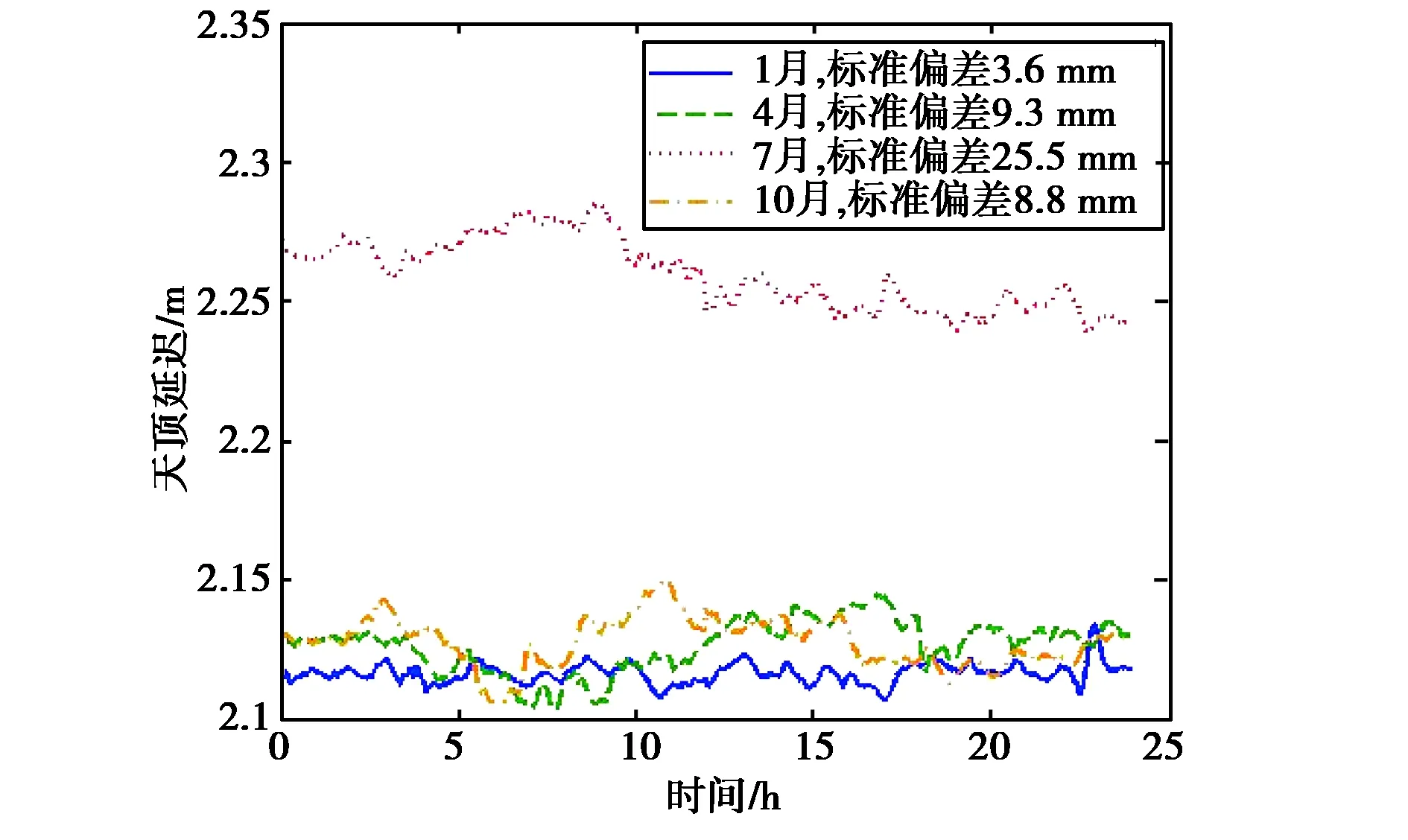
图7 乌鲁木齐24 h内大气延迟变化量

统计时间北京上海昆明乌鲁木齐2011.01.151.6×10-151.2×10-147.8×10-151.6×10-152011.04.153×10-141.2×10-132.9×10-141×10-142011.07.158×10-142.8×10-142.2×10-141.9×10-142011.10.151.8×10-144.5×10-142.5×10-149.3×10-15

表3 X/Ka频段的大气相位误差 (°)

由统计结果可知:大气结构常数越大,天线阵的大气相位误差越大,精度越低; 尤其是在Ka频段,上海4月和北京7月的相位误差均达到50°以上．由图3可知,这个量级的误差对于高频段天线阵通信系统来说,其增益损失是非常巨大的,会严重影响地面站与深空探测器之间的大容量通信．因此,长期统计深空站当地的大气扰动参数,准确评估大气扰动对天线阵通信系统工作性能的影响,可以有效地减轻、规避恶劣天气对系统造成的相位误差,使系统发挥更佳的通信性能．

5 结 论

作为目前深空通信天线阵系统中最大的误差源之一,对流层大气扰动随机相位误差已成为科研人员无法回避和容忍的影响因素．为了能够准确实时地反映不同深空站在不同时刻的大气扰动特性,通过利用单站GNSS接收机进行PPP解算天顶延迟,基于对流层天顶延迟与大气折射率的时变相关性获得了大气结构常数Cn,并统计了我国四个深空站典型月份一天24 h内的扰动特性和大气相位误差．统计结果表明,除了北京、乌鲁木齐在1月份的大气误差相对较小外,各站其他时间的大气扰动对深空站天线组阵高频段通信的影响都较为严重,尤其是上海的春季和北京的夏季．因此非常需要对我国不同区域、不同时间段的对流层大气扰动特性进行准确的量化统计,为我国向更远行星执行深空通信任务提供有效的环境信息服务保障．

[1] 于志坚. 深空测控通信系统[M]. 北京:国防工业出版社, 2009.

[2] ROGSTAD D, MILEANT A, PHAM T.Antenna arraying techniques in the deep space network[M]. Hoboken: John Wiley&Sons Inc, 2003.

[3] BAGRI D.Pros and cons of using arrays of small antennas versus large single-dish antennas for the deep space network[R]. IPN Progress Report, August 15,2008: 42-174.

[4] 姚飞, 匡麟玲, 詹亚锋, 等. 深空通信天线组阵关键技术及其发展趋势[J]. 宇航学报, 2010, 31(10): 2231-2238.

YAO F, KUANG L L, ZHAN Y F, et al. Key techniques and development trend of antenna arraying for deep space communication[J]. Journal of astronautics, 2010,31(10): 2231-2238.(in Chinese)

[5] PETRACHENKO W T, NIELL A E, COREY B E, et al. VLBI2010: next generation VLBI system for geodesy and astrometry[J]. Geodesy for planet earth, 2012, 136(1): 999-1005.

[6] GATTI M.A phased array antenna for deep space communications[C]//IEEE aerospace conference. Big Sky, Montana, USA, 2008: 1-8.

[7] BIANCO L, WILCZAK J M. Convective boundary layer depth: Improved measurement by Doppler radar wind profiler using fuzzy logic methods[J]. Journal of atmospheric & oceanic technology, 2002, 19(11): 1745-1758.

[8] NILSSON T, HAAS R. Impact of atmospheric turbulence on geodetic very long baseline interferometry[J]. Journal of geophysical research, 115(10), 2010:1-11.

[9] 朱庆林, 赵振维, 吴振森. 精密单点定位方法测量对流层天顶延迟的精度改善[J]. 武汉大学学报(信息科学版), 2009, 34(9): 1098-1101.

ZHU Q L, ZHAO Z W, WU Z S. Precision improvemen of tropospheric zenith path delay estimation by precise point positioning[J]. Geomatics and information science of Wuhan University, 2009,34(9)：1098-1101.(in Chinese)

[10]林乐科. 利用GNSS信号的地基大气折射率剖面反演技术研究[D].南京:南京邮电大学,2011.

LIN L K. Profiling tropospheric refractivity based on single ground-based GPS receiver[D]. Nanjing: Nangjing University of Posts and Telecommunications, 2011.(in Chinese)

[11]田耀佳. 单站GNSS估计对流层参数方法研究[D]. 青岛: 中国电波传播研究所, 2015.

TIAN Y J. Research of Tropospheric parameter Estimated with Singular Ground-based GNSS[D]. Qingdao: China Research Institute of Radio wave Propagation, 2015.(in Chinese)

[12]朱庆林, 吴振森, 赵振维, 等.单台地基卫星导航接收机测量对流层斜延迟[J].电波科学学报, 2010, 25(1): 37-40.

ZHU Q L, WU Z S, ZHAO Z W, et al. Tropospheric slant delay measured by singular ground-based satellite navigation receiver[J]. Chinese journal of radio science,2010, 25(1): 37-40.(in Chinese)

[13]NESSEL J A, MANNING R M. Derivation of microwave refractive index structure constant of the atmosphere from K-band interferometric phase measurements[J]. IEEE transactions on antennas and propagation, 2014, 62(11): 5590-5598.

[14]郝万宏, 董光亮, 李海涛. 无线电干涉测量在深空航天器导航中的应用[J].飞行器测控学报, 2009, 28(4): 1-6.

HAO W H, DONG G L, LI H T.An introduction to application of radio interferometry in deep space navigation[J]. Journal of spacecraft TT&C technology,2009, 28(4): 1-6.(in Chinese)

[15]姚飞, 詹亚锋, 陆建华. 深空通信天线组阵上行链路性能[J].清华大学学报(自然科学版), 2012, 52(9):1255-1259.

YAO F, ZHAN Y F, LU J H. Performance of an uplink antenna array for deep space communications[J]. Journal of Tsinghua University(science and technology), 2012, 52(9): 1255-1259.(in Chinese)

[16]D’ADDARIO L R. Estimates of atmosphere induced gainloss for the deep space network array[R/OL]. (2005-02-15)[2016-09-08].http://www.ipnpr.jp.lnasa.gov/progress-report42-160/160E. pdf.

Impact of atmospheric turbulence on the antenna array for deep space communication

ZHU Qinglin SUN Fang WANG Hongguang TIAN Yaojia LIU Kun ZHANG Lijun

(ChinaResearchInstituteofRadiowavePropagation,Qingdao266107,China)

atmospheric structure constant; atmospheric turbulence; troposphere delay; PPP; Deep space communications; antenna arraying; phase error

10.13443/j.cjors.2016090801

2016-09-08

国家自然科学基金(41305024)

TN011.3

A

1005-0388(2016)06-1067-07

朱庆林 (1981-),男,河南人,博士,中国电波传播研究所高级工程师,主要从事大气遥感、GNSS技术以及环境监测等工作．

孙方 (1982-),女,山东人,中国电波传播研究所高级工程师,主要从事电波传播、电波折射修正等方面的工作．

王红光 (1980-),男,河南人,博士,中国电波传播研究所高级工程师,主要从事对流层电波传播计算、大气波导、海杂波特性分析等方面的工作．

朱庆林, 孙方, 王红光, 等. 大气扰动对深空通信天线组阵性能的影响[J]. 电波科学学报,2016,31(6):1067-1073.

ZHU Q L, SUN F, WANG H G, et al. Impact of atmospheric turbulence on the antenna array for deep space communication[J]. Chinese journal of radio science,2016,31(6):1067-1073.(in Chinese). DOI: 10.13443/j.cjors.2016090801

联系人： 朱庆林 E-mail: 185730117@qq.com

DOI 10.13443/j.cjors.2016090801