基于Matlab的线性二次高斯控制教学——以旋翼飞行机器人的控制为例

陈阳，吴春富，马桂芳

（龙岩学院机电工程学院，福建龙岩364000）

基于Matlab的线性二次高斯控制教学
——以旋翼飞行机器人的控制为例

陈阳，吴春富，马桂芳

（龙岩学院机电工程学院，福建龙岩364000）

以基于线性二次高斯控制的旋翼飞行机器人的速度跟踪稳定控制为例，在Matlab软件中进行编程计算及仿真，将抽象的线性二次高斯控制问题具体化，并就代价函数参数矩阵的选择对系统的控制响应性能的影响进行了分析.整个建模仿真过程能够帮助学生理解和掌握线性二次高斯控制理论.

线性二次高斯；旋翼飞行机器人；计算机辅助教学

在现代控制理论课程中，线性二次高斯（LQG）控制一般安排在该课程的最后教学环节中，其涉及了该课程前期的系统状态空间描述、能控制、能观性及稳定性等理论，通过LQG控制技术的学习能够将现代控制理论教学内容有机地结合起来［1］.然而实际教学往往采用公式推导的方式开展理论教学，导致学生对这一现代控制技术理解不够深入.特别是LQG控制技术中涉及的状态空间方法有着实际工程背景，其状态转移矩阵描述了被控对象的内在联系.在一些复杂系统的控制中，LQG控制技术设计的控制器能够考虑到系统状态之间的耦合关系，因此其在雷达天线的旋转跟踪控制［2］，船舶的运动控制［3］，飞行器的飞行控制［4］,汽车悬架控制［5］等领域都得到应用.基于LQG控制技术是一项与实际工程的模型系统密切相关的理论技术的考虑，如何帮助学生形象地理解并掌握LQG控制技术是教学中的难点.

本文以实际科研过程中的旋翼飞行机器人水平面动力学模型的速度跟踪稳定控制为例，进行控制器设计，由于旋翼飞行机器人与生俱来的动力学状态耦合［6］，采用LQG控制技术能够综合考虑系统状态间的联系.本文将基于Matlab控制系统辅助设计软件进行LQG速度跟踪稳定控制器的设计、仿真与分析，并对LQG设计过程中涉及到的两个关键权值矩阵对系统响应性能的影响进行分析，整个系统在Matlab的Simulink环境中进行仿真，形象直观，利于学生掌握线性二次高斯控制理论的各个环节.

1 基于LQG技术的旋翼飞行机器人的姿态稳定控制

1.1 旋翼飞行机器人水平面动力学模型描述

当小型旋翼飞行机器人工作于悬停或低速飞行状态下时，其动力学可分为耦合性可以忽略的两个部分：一是作用于水平面的动力学，二是作用于垂直面的动力学，其中水平面的动力学主要由主旋翼产生的横向与侧向运动构成.此时旋翼飞行机器人用于控制律设计的水平面线性化模型的状态空间表示形式如下式所示：

其中，系统状态向量x=[u v θ φ q p asbs]T，u与v分别为前向及侧向线速度、θ与φ分别为俯角及滚转角、q与p分别为俯仰角速率及滚转角速率、as与bs为带有伺服小翼的旋翼挥舞运动在俯仰及滚转通道的描述.系统控制向量u=[B1sA1s]T，B1s及A1s分别为俯仰及偏航通道的控制量.状态转移矩阵A、控制矩阵B及观测矩阵C分别为：

式（2）矩阵C中的I6×6为6阶单位矩阵，O6×6为6行2列的零矩阵.对于式（1）及式（2）所示的线性时不变系统，其状态转移矩阵A的特征值为系统的极点，可以体现系统的稳定性［1,7］.在Matlab中通过命令Eig函数可以求出矩阵的特征值及特征向量，通过分析特征值与特征向量可以分析系统的动力学特性［7］，包括稳定性与否，每种模态的固有频率、阻尼比，以及系统中每个状态量对给定输出的贡献程度的大小.表1所示为旋翼飞行机器人水平面模型对应的8个特征值，可以发现其中存在两个包含正实部的特征根，此组特征值对应旋翼飞行机器人的非稳定模态，主要由前向及侧向速度引起，可知系统不能长时间保持稳定悬停状态，这与实际情况相符.因此小型旋翼飞行机器人在悬停或低速飞行时，其在长周期模态下是不稳定的.

表1 旋翼飞行机器人水平面模型的系统极点

1.2 基于LQG的速度姿态稳定跟踪控制

从上一节可以发现，旋翼飞行机器人的水平面动力学模型的状态转移矩阵包含一对非稳定的特征根，因此需要控制器镇定其中的非稳定模态以保证飞行机器人的稳定控制.另一方面，从旋翼飞行机器人的线性模型可以知道，水平面模型中的状态量as及bs不能通过传感器直接测量出来.实际工程中的LQG设计是通过将线性二次状态反馈调节器（LQR）与观测器结合起来而完成的.一方面LQR技术将镇定系统的非稳定状态，另一方面观测器将估计系统中的非测量状态，同时能够很好地跟踪参考线速度uref及vref.整个控制器设计依据分离原则，包括LQR设计及线性二次估计（LQE）设计两部分.图1所示为在Matlab/Simulink中搭建的基于LQG的飞行机器人速度跟踪控制器仿真图、其中的前馈环节、积分环节及反馈环节的参数由LQR设计，估计器由LQE设计.

图1 Matlab/Simulink中进行LQG控制器仿真

1.2.1 LQR跟踪控制器

LQR控制器考虑了系统本身的耦合特性以镇定旋翼飞行机器人，同时控制器中的积分及前馈两个环节是为了提高跟踪精度及响应速度.

为考虑系统对给定速度的跟踪性能，将系统（1）增加性能输出向量z如下：

参考指令r(t)与性能输出z(t)之差表示为e=r-z，则e的积分为并定义新的状态向量为x^=得到新的状态方程为：

式（5）中Q是一半正定对称矩阵，R为正定对称矩阵.应用最优控制理论［1,7］可得优化控制器如下：

式（6）中控制参数kx^及kr可通过Matlab中Lqr函数求得.

1.2.2 LQE设计

考虑线性系统模型式（1）包含扰动的形式如下：

式（7）中w为过程噪声，v为观测噪声，并假设为互不相干的零均值高斯白噪声，且协方差矩阵分别为Qf及Rf.则可得优化估计器为：

式（8）中估计增益kf可通过Matlab中Lqe函数求得.

2 Matlab中仿真实验分析

在使用LQG技术进行速度姿态稳定跟踪控制时，从式（6）可知，矩阵Q及R分别是一个4维及2维的对称方阵，为了简化计算，实际中分别取Q及R为对角矩阵，根据LQR相关优化理论可知，大致有当Q阵中某一元素的权值增大时，与其对应的状态量的动态响应过程好转，系统快速性得到明显提高，但相应地引入一些振荡；当R中某一元素权值增大时，被控量幅值显著减小，对应的动态性能有所改善，但不显著.故首先通过在Matlab上针对不同Q、R下通过编程进行控制器计算，而后在Matlab中的Simulink环境中进行仿真，最后对比相关性能选取一组较为合适取值下的控制器参数.解算LQE估计器时涉及的Qf及Rf分别取为：Qf=0.001I8×8，Rf=0.001I6×6.

图2 Q=diag(0.3,0.6,0.018,0.036)，R=diag(15,10)下速度跟踪响应

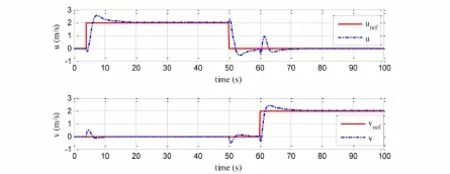
图3 Q=diag(0.3,0.75,0.015,0.0375)，R=diag(15,20)下速度跟踪响应

图4 Q=diag(0.3,0.6,0.0075,0.015)，R=diag(20,10)下速度跟踪响应

图5 Q=diag(4,3,0.16,0.12)，R=diag(37.5,50)下速度跟踪响应

图2～5所示为不同Q、R下，基于扩展LQG控制器的前向及侧向目标速度跟踪响应图，可以发现4种Q、R取值情况下，速度跟踪响应曲线都有一定程度的超调，但最后都回归到了稳态，实际上前馈部分的引入在加快系统响应的同时，另一方面也引入了一定的超调，尽管如此，通过调节Q、R值，能够在超调与响应时间之间得到一个折衷的选择.为进一步比较上述四种不同Q、R取值情况下的控制系统响应性能，定义三个性能指标，一是阶跃响应上升时间为：系统响应从0%到最终值95%所需的时间；二为最大超调量：（系统阶跃响应最大值—系统阶跃响应稳态终值）/系统阶跃响应稳态终值；三为系统阶跃响应与设定值之间的均方差；表2展示了不同Q、R取值情况下横向及侧向速度的跟踪性能.

表2 不同Q、R取值情况下横向及侧向速度的跟踪性能比较

表3 旋翼飞行机器人增广水平面模型镇定后的极点

从表2可以看出，不同Q、R取值下得到的控制器对前向及侧向目标速度的跟踪性能在三个指标上具有差异性，从系统的响应速度上来说，矩阵Q上的值越大，对应目标速度跟踪响应越快，但是从表中对比可以发现，控制系统对目标速度的响应时间、超调量及跟踪精度不可能所有都达到最优，亦即当最大超调量为小时，系统的上升时间未必为短，如此，在实际控制器参数选择时，需要进行一个折衷的考虑，根据上表可以发现，不同参数下得到的控制器对目标前向速度的响应时间在1.861～2.087 s之间，对目标侧向速度的响应时间在1.488～1.622 s之间，当飞行机器人工作于悬停及低速飞行状态时，可以认为此长度的响应时间对飞行机器人的飞行影响不大，因此上升时间的指标不作为实际控制器设计的一个重要指标.考察最大超调量及速度跟踪均方差两个指标时，发现基于第三种Q、R参数下所得到的控制器产生的响应性能相对较优（超调与MSE均较小），故选择此情况下得到的控制器用以实现水平面模型的速度姿态稳定跟踪控制.表3所示为第三种参数下旋翼飞行机器人增广水平面模型镇定后的极点，相比较于表1，可发现非稳定极点得到了镇定.

3 结论

本文针对线性二次高斯控制问题，以实际科研中涉及的旋翼飞行机器人的水平动力学速度跟踪稳定控制为例，利用Matlab语言编程，分析了模型的稳定性，而后求解速度姿态稳定控制器，并针对LQG中涉及的参数矩阵的不同取值进行了仿真分析，在教学中实现了把抽象现代控制理论知识具体化和形象化，加深了学生对相关概念的理解，提高了学生应用Matlab解决控制问题的能力.

［1］俞立.现代控制理论[M].清华大学出版社,2007.

［2］Gawronski W.Modeling and Control of Antennas and Telescopes[M].Netherlands:Springer,2008.

［3］Zhang G,Li P.Augmented LQG Method for Optimal Control of Ship Shaft-Generator[J].Journal of Convergence Information Technology,2013,8(1):362-372.

［4］Minh L D,Ha C.Modeling and Control of Quadrotor MAV using Vision-based Measurement[C].International Forum on Strategic Technology,2010:70-75.

［5］刘海生.Simulik在汽车主动悬架LQG控制仿真中的应用[J].机械设计与制造,2008(8):106-107.

［6］Cai G,Chen B M,Dong X,et al.Design and Implementation of a Robust and Nonlinear Flight Control System for an Unmanned Helicopter[J].Mechatronics,2011,21(5):803-820.

［7］郑大钟.线性系统理论[M].北京：清华大学出版社，2012.

Teaching Linear Quadratic Gaussian Control Based on Matlab——A Case Study of the Stability Control of a Rotor Flying Robot

CHEN Yang,WU Chun-fu,MA Gui-fang
（1.School of Mechanical and Electrical Engineering，Longyan University，Longyan 364000,Fujian，China）

The velocity tracking control of the rotor flying robot based on the Linear quadratic Gaussian(LQG) technique was taken as an example which was programmed and simulated in MATLAB.The abstract linear quadratic Gaussian control problem was specific,and the parameter matrix of the cost function which will influence the system's control response performance was analyzed.The processing of the modeling and simulation can help students to understand and master the linear quadratic Gaussian control theory.

linear quadratic Gaussian;rotor flying robot;computer-aid instruction

G642.0

A

1007-5348（2016）12-0078-06

（责任编辑：邵晓军）

2016-07-06

福建省中青年教师教育科研项目（JA15492）；龙岩学院2014年教改项目（2014JY38）.

陈阳（1985-），男，福建龙岩人，龙岩学院机电工程学院讲师；研究方向：飞行机器人导航制导与控制.