小学数学“可能性”教材分析与实践思考
刘圣良
“可能性”是人教版义务教育教科书数学五年级上册第四单元教学内容,属于“统计与概率”领域的内容。在小学阶段,仅安排在第二学段学习。在原义务教育课程标准实验教材中,此部分教学内容分两次集中编排。第一次安排在三年级上册,教学目标是让学生初步体验确定事件和不确定事件,初步感受事件发生的可能性有大小。第二次安排在五年级上册,教学目标是使学生对“可能性”的认识和理解逐渐从定性向定量过渡,学会用分数描述事件发生的可能性大小。数学课标修订后,在人教版教材第一学段中,删掉了概率的学习,将原内容后移到第二学段,称为“可能性”。原五年级的内容划分到第三学段,称为“概率初步”。人教版五年级义务教育教科书关于“可能性”的内容虽然只有三道例题,却承载着概率教学中非常重要的任务,每道例题具体教学目标不同,甚至“做一做”和某些习题也承载着重要的任务,这一单元的教学是衔接中学概率教学的重要基石。由于概率的发展较其他领域的内容晚,教师对此部分内容的数学核心素养模糊不清,加上新教材对该部分内容又有较大调整,并且增添了新例题(如例3)。所以,教学这部分内容,对于教师来讲有一定的难度。这就要求教师要抓住知识的纵向联系,站在知识的高位,自上而下分析教材、吃透教材,要从数学核心素养的培养来定位教学目标,设计教学活动。
一、从中学的“概率”教学看小学的“可能性”教学
(一)中学教材中的概率内容的数学概念解读
中学教材对随机事件、概率的两个意义(概率的古典意义和概率的统计意义)进行了具体描述。
1. 随机事件。
在一定条件下,某些事件有可能发生,也有可能不发生,这样的事件称为随机事件。
2. 概率的古典定义。
一般来说,如果一次实验中,有n种可能的结果,并且他们发生的可能性都相等,事件A包含其中的m种结果,那么事件A发生的概率为P(A)=。比如,掷两枚硬币实验,分析出现一正一反的可能性大小。在一次实验中,可能出现四种情况:第一种,1号币正面、2号币正面;第二种,1号币正面、2号币反面;第三种,1号币反面、2号币正面;第四种,1号币反面、2号币反面。一正一反有两种情况,占了,概率则为。
3. 概率的统计意义。
一般来说,在大量重复实验中,如果事件A发生的频率m/n会稳定在某个常数p附近,那么这个常数p就叫做事件A的概率。比如,掷一枚质地均匀的硬币,出现正面或反面朝上的概率是多少?从统计意义出发,首先要反复做掷硬币实验,经过大量实验,统计数据,求出正面或反面朝上的频率(正面或反面出现次数占总次数的比率),随着实验次数的增加,这个频率会稳定在0.5这个常数左右,这个常数0.5就是正面或反面朝上的概率。
实际上,概率的古典定义具有一定的局限性,有一些随机实验并不具备有限与等可能性质,对于这类随机实验,概率的古典定义不能适用。比如,考查某种树苗的移植成活率、某种子的发芽率、估计某射击运动员的命中率、某水果运输过程中的损坏率等。这些实际问题都不属于各种结果可能性相等的类型,所以不能用古典定义来求,而要用统计意义来求。如某林业部门要考查某种树苗在一定条件的移植成活率,应采取什么样的具体做法呢?首先,在同样的条件下,大量地对这种树进行移植(移植的棵树用字母n来表示。),并统计成活情况(成活的棵树用字母m来表示。),然后计算成活的频率(m/n)。如果随着移植棵树n的增加,频率越来越稳定于某个常数,那么这个常数就可以被当做作成活率的近似值。
(二)中小学概率教学的衔接
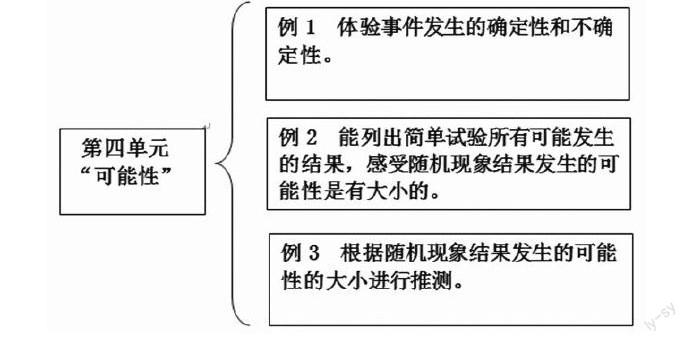
中学的概率教学是从概率的两个意义(古典意义和统计意义)为出发点,然后过渡到求概率的内容。即,用列举法求概率和用频率估计概率。人教版义务教育教科书单元知识框架图如下:
1. 从教学的知识目标和教学内容来看衔接。
小学阶段以感性认识可能性为主,通过实验去感受随机性,定性描述可能性大小,初步根据结果推测状态。虽然是感性的认识,但是与中学的衔接很紧密。实际上三道例题是中学随机事件和概率的意义的雏形。例2、例3是学生了解概率的统计意义的铺垫。而“做一做”(抛硬币活动)也是学生理解概率统计意义的有效载体,这个数学活动也是中学教材中的例题。
2. 从教学的过程目标和核心素养来看衔接。
中小学都是通过摸球、抛硬币等活动感受和体会随机性。体现在两个方面:一个是单次事件发生的不确定性(偶然性),一个是大量实验结果统计的规律性。这种随机性是学生通过调查研究,收集数据,通过分析做出判断的过程中体验到的。小学强调推测球或棋子的分布情况,即谁多谁少。中学要计算出频率,推测概率。可以看出,数据分析是中小学教学概率内容的重要方法。《数学课标标准(2011年版)》把数据分析纳入到十个核心概念之一,强调要注重发展学生的数据分析观念。关于数据分析观念,具体阐释为:“了解在现实生活中有许多问题应当先做调查研究,收集数据,通过分析做出判断,体会数据中蕴含的信息;了解对于同样的数据可以有多种分析方法,须要根据问题的背景选择合适的方法;通过数据分析体验随机性,一方面对于同样的事情每次收集到的数据可能不同,另一方面只要有足够的数据就可能从中发现规律。”在这段话中,点明了统计的核心是数据分析,东北师大马云鹏教授提出:数据分析观念是中小学学生学习统计与概率内容的数学核心素养。由此,笔者认为数据分析观念也是中小学统计与概率教学的重要衔接点。在前面教材分析的基础上,笔者带领着团队教师进行了一些教学实践,下面结合几个案例来谈一谈小学教学“可能性”内容落实数据分析观念的粗浅认识与思考。
二、 从借助“数据分析” 入手, 教学小学阶段的“可能性”内容
数据分析观念很抽象,教师如果仅把它作为一种观念或思想,教学中很难落实。笔者认为,把数据分析看作是一种学生学习的手段、策略、方法,就很容易操作。在课堂上,让学生经历数据分析的过程,掌握数据分析的基本方法,通过数据分析感受随机性,这样才能有效落实“可能性”的教学目标。
1.让学生经历“猜测——实验——数据分析——推测结论”的过程,丰富学生的体验,感受事件发生的随机性。
一线教师对这部分教学存在困惑:概率的教学需不需要实验?实验后频率和概率之间差距大了怎么解释?实验结果不能验证概率的大小,学生越学越糊涂,怎么办?比如,“掷硬币实验”是“验证”正面和反面朝上的可能性相等,还是“推测”正、反面朝上的可能性相等。如果站在验证的角度,教师就容易出现上面的困惑。如果是借助实验数据,包括科学家的数据分析来推测可能性,这里即使出现极端数据,我想也很容易解释,实验次数少的情况下,就会出现所谓的“运气差”的偶然性,这就是随机性。所以要引导学生看整体数据,增加实验的次数,只有实验的次数越来越多时,才会呈现统计的规律性。教师要引导学生根据这种规律性去推测可能性的大小。教材编排的几道例题都是基于这样的目的,呈现“猜测——实验——数据分析——推测结论”的过程,丰富学生的体验,感受事件发生的随机性。
一位教师执教“可能性例1”时创设了班级抽奖情境,每次学生抽签之前,教师都是让学生先猜测抽签的结果,(可能抽到什么?不可能抽到什么?)然后再实验,通过猜测——实践——验证的过程让学生感受事件发生的确定性和不确定性。
一位教师执教“可能性例2”时创设了摸棋子游戏情境。课伊始,教师拿来一个装有两种颜色棋子的盒子,呈现里面红色棋子和白色棋子的数量,提问:“摸出一个棋子可能是什么颜色?”生:“红色或白色。”师:“猜一猜摸到哪种颜色的棋子可能性大?”(学生凭直觉很容易说出红色的可能性大,因为红色的棋子多。)这时,教师话锋一转,“这只是我们的猜测,需要实验验证一下我们的猜测”。此时,教师引导学生进行分组实验,记录数据,分析数据,推测前面的猜想,进而得出哪种颜色棋子多,摸到它的可能性就大。在这个过程中,不仅丰富了学生对不确定现象的体验,而且加深了学生对随机事件统计规律性及事件发生可能性大小的直观感受。
让学生经历“猜测——实验——数据分析——推测结论”的过程是可能性教学的基本思路,也是培养学生数据分析观念的重要流程。因为在这个过程中学生能体会到收集数据、统计数据、分析数据的价值,感受到数据分析是预测和推测一件事情必须经历的过程。如果课堂上能够形成“我要收集数据”“必须分析数据”“我用数据说话”这样的思维过程,那么,学生的数据分析观念已经初步形成了。
2. 有效设计问题引领学生聚焦“数据”,实现从猜测到推测的过程,培养数据分析观念。
如何引领学生聚焦数据,自觉收集、分析数据,实现从猜测到推测的过程?教师有效设计问题,有利于学生聚焦数据,培养数据分析观念。
一位教师执教“可能性例3”时创设了摸球活动情境。引导学生猜一猜:盒子里面哪种颜色的球多?然后统计选择的人数:25人选择黄色,14人选择白色,再引导学生进行实验。首先,让两名学生到前面每人摸3次,让学生再猜。学生感受到次数少,不能说明问题。然后,组织全班学生进行小组摸球,分组记录数据,再汇总全班数据。最后,教师让学生观察数据,再猜测摸到哪种颜色球的可能性大,即哪种颜色的球数量多。统计选择的人数:黄色的人数为3人,白色的人数为36人。此时,教师提出一连串问题,让学生聚焦到数据分析,交流碰撞。
师:仍然选择黄色的同学请起立,老师采访一下,为什么你还坚持选黄色球?
生:我们组摸到的黄色球的次数多。
师:改变选择的同学请举手,老师采访一下你们,为什么你们改变了选择?
生:因为摸到白色球的可能性大。
师:那第6组实验数据,确实是摸到黄球的次数多呀。
生:我们不能只看这两组数据,大多数组都是摸到白球的次数多。
师:只看一组数据行不行?可以看多组数据,还可以怎么办呢?
生:把它们加起来,看看整体数据。
师:汇总数据后,你有什么发现?
整个活动过程,教师没有指令学生该进行哪一个环节?是在教师和学生共同探讨数学问题的驱动下发展的,学生逐渐的感受到,实验次数少,要多次实验,即我要做实验,收集数据。当呈现全班数据时,教师设计了环环相扣的问题串,引导学生感受到收集数据是必要的,分析数据是必须的;体验到数据蕴含着信息,只有通过大量数据信息的分析,才能做出合理的判断。在这个过程中,学生不仅体验到事件的随机性,而且数据分析观念得到有效培养。
3.教师要有效指导实验,保证数据的随机性和统计的准确性,才能形成统计的规律性。
为了保证数据的随机性,教师在实验前要提醒学生明确实验的要求和目的,深入学生活动中有效指导,确保实验的有效性。千万不要出现学生偷看盒子、不摇盒子等现象,这些现象可能都会导致数据的极端化,而使数据失去随机价值。我们知道,统计的规律性一定是建立在随机抽取的数据基础上,也就是说,当大量重复实验时,随机抽取的数据越来越多时,统计的数据才能呈现一种规律性。在这个过程中,统计数据至关重要。为了保证统计的准确性,可以运用现代信息技术手段(计算器、电子表格求和),跟学生一起统计数据,保证数据统计的准确性。只有保证了数据的随机性和统计的准确性,才能使统计的数据逐步呈现出规律。但是,一旦出现了规律不明显或者矛盾的规律(错误的规律), 怎么办?我觉得教师要引导学生再多做一些重复的实验,获得更多的数据,还要跟学生一起分析实验数据,分析实验条件中是否存在问题(如是否摇匀,是否偷看了,是否统计出错等)。
总之,概率教学离不开统计数据、分析数据。教师要不断研究教材,理清知识的横纵向联系,站在知识的上层建筑,围绕数学核心素养“数据分析观念”设计教学、实施教学,才能使数学课堂焕发活力,才能彰显数学学科的魅力。
编辑∕宋 宇

