关于散度和旋度教学的几点思考
杜晓燕, 张秀钢, 陆杰青
(信息工程大学, 河南 郑州 450002)
关于散度和旋度教学的几点思考
杜晓燕, 张秀钢, 陆杰青
(信息工程大学, 河南 郑州 450002)
散度和旋度是研究电磁现象的重要工具,由于其定义抽象、计算复杂,一直是电磁理论教学过程中的重点和难点。本文就实际教学过程中,学生容易发生混淆或难以理解的旋度的计算、散度和旋度的联系、亥姆霍兹定理等知识点进行了讨论,帮助学生很好地掌握这一内容。
电磁场; 散度; 旋度
0 引言
散度和旋度是电磁理论教学中的重要内容,不仅其定义、计算要求学生熟练掌握,与其相关的定理也要求学生深刻理解。
这两个知识点的教学思路通常是:先结合通量的介绍,引出散度的定义,再推导散度的计算公式,然后介绍散度定理;与此相同,结合环量和环量面密度介绍旋度,再推导旋度的计算,然后介绍旋度定理[1~5]。教学过程中,也会结合水流、漩涡、礼花等一些日常现象来帮助学生掌握这些概念[6]。
教学过程中通常将散度和旋度割裂开,分别予以介绍,并不重视讨论其异同之处。这常常导致学生产生不必要的误解:如认为两种源——通量源和涡旋源是相互无关的等。
针对上述问题,笔者在实际教学过程中着重就旋度的计算、散度和旋度的联系与区别等进行了讨论,帮助学生很好地掌握这些知识点,而且对其相关内容的学习也起到了很好的促进作用。
1 散度和旋度的联系与区别
由定义可知,散度为单位体积内矢量场的通量,即通量分布的体密度。
(1)
而旋度则是指单位面积上矢量场的环量,而且这个环量必须是最大值。
(2)
1.2 计算过程
由定义可知,散度的计算过程如图1所示。

图1 散度计算过程
而旋度的计算过程如图2所示。
(二)离合词“A了个B”与网络语“A了(嘞)个B”在不同的语体中使用。前者一般在书面语体中或是在正规场合的口语中出现。而后者则主要出现在网络即时工具聊天,网络游戏或者网络论坛中,不过现在也开始“入侵”到非正规场合的口语中,用以表示幽默和时髦。如:

图2 旋度计算过程
1.3 旋度计算中的优化问题
相较于散度,旋度增加了求极值的过程,这是导致旋度计算复杂、难以理解的主要原因。
此处,结合旋度计算,我们引入优化问题:如何求极值,为此设置相应研讨题目。
研讨题目1:如何利用矢量场论的知识进行标量场极值问题的求解。
研讨内容:让学生通过讨论两个矢量的点积了解到:两个方向垂直的矢量场的点积是0,由此掌握了求解点积最小值的两个矢量场的方法;而通过讨论两个方向相同的矢量场的点积是1,由此掌握了求解点积最大值的两个矢量场的方法。
通过以上学习,学生不仅很好得理解了“旋度的大小是此处最大环量面密度”这一结论,而且对矢量点积运算有了更深入的认识。
1.4 通量源和涡旋源的异同
散度和旋度最为重要的意义在于它们描述了两类激发出场的源--通量源和涡旋源[1~8]。
引入哈密顿算符后,在直角坐标系中,散度和旋度的计算公式分别简化为

(3)

(4)
不难得出,通量源只影响场的各个方向分量沿自己方向的变化,而涡旋源只影响场的各个方向分量在与自己方向相垂直的另外两个方向上的变化,即具有旋转特性。上述性质,很多文献中都有讨论,本文不再赘述[1~8]。
1.5 亥姆霍兹定理中的散度和旋度
亥姆霍兹定理是场论中的重要定理,为场的研究提供了理论依据。
其内容为:对于有限空间中的任意矢量场,如果可以确定其散度、旋度和边界条件,就可以唯一确定这个矢量场。
除限定所研究场的空间区域的边界条件外,散度和旋度是亥姆霍兹定理中的主要内容。由定理可知,对于任意矢量场,只知道其散度或旋度中的一个,是无法唯一确定这个矢量场的,即散度和旋度中各包含了矢量场的不同性质,如文献[4]中所述;在研究场的问题时,两者相互补充、缺一不可。
由于本科生“电磁场理论基础”教学过程中不要求亥姆霍兹定理的证明,且该证明也有一定难度。教学过程中我们参考文献[8],通过引入矢量除法,帮助学生深刻理解定理内容,
众所周知,已知两个标量的乘积及其中任意一个标量,由除法可以唯一确定另一个标量。而场论中讨论的矢量乘法主要有点积、叉积和三重积,但鲜有讨论矢量除法的公开报道。那么,已知两个矢量的点积或叉积及其中任一个矢量,能否唯一确定另一个矢量呢?授课过程中,我们参考文献[8]设置了相应研讨题目。帮助学生更深入地理解散度和旋度的联系与区别。

图3 两个不同矢量在x轴上投影相同
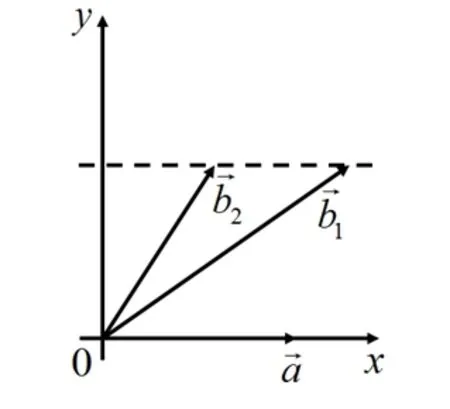
图4 两个不同矢量在y轴上投影相同
研讨内容:由矢量代数的知识,可以很容易推导得到[8]:
(5)
点积和叉积是将一个矢量作用到另一矢量上,而散度和旋度是将矢量微分运算符——哈密顿算符作用到一个矢量上。
所以,关于点积和叉积的研究与散度和旋度的研究在矢量方向的运算上是完全相同的。区别仅在于散度和旋度还伴随有微分运算。
由此,就可以将亥姆霍兹定理的内容与矢量除法的结论相对照,帮助学生很好得理解定理的内容,进一步明确在研究矢量场特性时,散度和旋度描述了矢量场的不同特性,两者相互补充、缺一不可。
2 结语
散度和旋度是电磁理论教学中的重要内容,也是研究电磁场问题的基础,要求学生熟练掌握,深刻理解。本文就散度与旋度讲授过程中易发生混淆的几个问题进行了讨论,帮助学生进一步明确了散度和旋度的联系与区别等,为深入学习电磁场相关内容打下了良好的基础。
[1] 毕德显.电磁场理论基础[M]. 北京:电子工业出版社.1985.
[2] Bhag Singh Guru,Huseyin R.Hiziroglu 著,周克定等译. 电磁场与电磁波[M].北京:机械工业出版社.2000.
[3] 龚中鳞.近代电磁理论[M].北京:北京大学出版社.2010.
[4] 陈重等.电磁场理论基础[M].北京:北京理工大学出版社.2008.
[5] 苏东林.电磁场与电磁波[M],北京:高等教育出版社,2009.
[6] 黄辉,张小青.“电磁场”课程的散度和旋度研究型教学例析[J]. 南京:电气电子教学学报. 2011 ,(33)3:99-102.
[7] 刘德国.“电磁场”课程中梯度、散度、旋度教学方法探讨[J]. 济南: 科技信息. 2014 , 15:51-52.
[8] 梁昌洪.矢量场论札记[M],北京:科学出版社,2007.
The Study on Teaching of divergence and curl
DU Xiao-yan, ZHANG Xiu-gang, LU Jie-qing
(InformationEngineeringUniversity,Zhengzhou450002,China)
Divergence and curl are important tools in research on electromagnetic phenomenon. For abstract define and complex calculation, divergence and curl are key points and difficulties in the teaching of Electromagnetism. This paper presents discussion, aiming at the difficultis such as the calculous of curl, the relationship bteween divergence and curl, knowledge points of Helmholtz′s theorem. All these works plays an active role for the understanding of divergence and curl.
electromagnetic fields;divergence;curl
2015-10-23;
2015-12-05
杜晓燕(1975-),女,博士,副教授,主要从事电磁场与微波技术、天线等方面的教学与科研工作,E-mail:chaomei-z@163.com
TN91
A
1008-0686(2016)05-0081-03

