基于外加电流源研究梯形网络的等效电阻
胡菊菊, 柯 强, 嵇英华
(江西师范大学 物理通信电子学院, 江西 南昌 330022)
基于外加电流源研究梯形网络的等效电阻
胡菊菊, 柯 强, 嵇英华
(江西师范大学 物理通信电子学院, 江西 南昌 330022)
本文将线性空间的不动点理论与施加双外加电流注源法相结合,在探索研究网孔电流的递归表达式的基础上,给出了一种求Z×N级梯形电阻网络输入端任意两节点间等效电阻的简捷计算方法。该计算方法对计算平面电阻网络的等效电阻不仅有通用性,而且更加方便灵活。
阶梯形网络;差分矩阵;等效电阻
0 引言
梯形电阻网络在工程实践中有不少的应用,是一种重要的物理研究模型。文献[1]根据基尔霍夫电路定理,应用支路电流法与矩阵变换,求解了2×N阶梯形电阻网络的等效电阻。由于文中选择了支路电流作为参变量,导致推导过程有些繁琐。文献[2] 通过考虑电桥平衡,给出了2×N阶梯形电阻网络的等效电阻,方法比较简便,但解法的通用性受到一些限制。
众所周知,对于平面电路,将网孔电流作为参变量,可以减少方程的数量,从而大大地简化运算。本文基于不动点理论,应用双外加电流源法,给出了求解2×N梯形电阻网络等效电阻一种新的通用且简便的方法。
1 模型与网孔方程
研究图1所示的2×N阶的梯形电阻网络,图中电阻r、r0与r1均为N个。

图1 2×N阶梯形电阻网络
采用网孔电流法可以很方便地求解每一支路的电流与电压。此外,根据电路理论,计算端口的等效电阻可以采用外加电流源法。
在图2中,我们将电路网络拓展为2×(N+1)阶,最左侧网孔的电流即为外加电流源,外加电流源电流记为Is1与Is2。为计算方便,图2中假设位于上面一层的网孔电流为I↑mk;位于下面一层的网孔电流为I↓mk(k=1,2,…,N+1 );每一个网孔电流的绕行方向均取为顺时针方向。
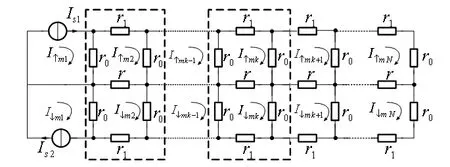
图2 外加双电流源求解2×N阶梯形电阻网络
针对虚线框中第k列的上、下二个网孔,列出网孔电流方程为
(2r0+r+r1)I↑mk-r0(I↑mk+1+I↑mk-1)-rI↓mk=0
(1)
(2r0+r+r1)I↓mk-r0(I↓mk+1+I↓mk-1)-rI↑mk=0
(2)
对上面两个方程进行和与差的重新组合,得到:
(3)
式中
方程式(3)为一个差分矩阵方程。根据不动点理论,该差分矩阵方程对应的特征方程为
x2-ax+1=0
(4)
y2-by+1=0
(5)
两组特征根(x1,x2)、(y1,y2)分别为
(6)
(7)
2 电流的通项公式
由方程式(3)-式(7),容易得到第k列上下二层网孔电流和与差的通项公式
(8)
(9)
式中
(10)
利用广义的基尔霍夫节点电流定理
(11)
(12)
容易得到如下关系式:
(13)
(14)

(15)
(16)
联立求解方程式(13)-式(16),得
(17)
(18)
容易得到在外加电流源作用下,通过图1第一列上下支路电流为
(19)
(20)
3 梯形电阻网络的等效电阻
由式(17)-式(18),应用外加电流源法,可以非常容易得到任意端口上的等效电阻
(1)对端口a-b,令Is2=0,有
(21)
(2)对端口b-c,令Is1=0,有
(22)
这正是文献[1]给出的结果,也包含了文献[2]给出的电桥平衡下的结果。通过选择网孔电流为参变量,施加双外加电流源,使得解法更具有通用性,处理问题更加方便灵活。显然,如果要计算图1右侧相应点的等效电阻,根据对称性,应有Ra′b′=Rab,Rb′c′=Rbc。如果要计算上(下)边相应两点间的等效电阻,也可采用类似的外加电流源法进行推导。
4 结语
本文应用不动点理论,给出了2×N阶梯形电阻网络等效电阻的一般分析方法。从前面的分析计算过程可以看到:选择网孔电流为参变量,在待求端口施加外加电流源,可以方便地给出端口处的等效电阻。整个求解过程思路简捷清晰,对同类型的平面电路具有通用性,且能够推广应用于平面的正弦稳态电路。
[1] 谭志中, 罗礼进. 2×n阶电阻网络等效电阻的再研究[J]. 南通: 南通大学学报(自然科学版),2010,9(1):86-89
[2] 刘松山. 基于对称性研究2×n阶梯形电阻网络等效电阻[J]. 北京: 大学物理, 2015, 34(1):26-29
Equivalent Resistance of Ladder Resistance Network Based on External Current Source
HU Ju-ju, KE Qiang, JI Ying-hua
(CollegeofPhysicsandCommunicationElectronics,JiangxiNormalUniversity,Nanchang330022,China)
This paper investigates the recursive expressions of mesh current based on fixed point theory of linear space under double external current source, and proposes a simple method to solve the equivalent resistance between arbitrary two input nodes of a Z×N ladder resistance network. The calculation method is general and simple.
ladder network; difference matrix; equivalent resistanc
2015-11-05;
2016-04-06 基金项目:江西省高等学校教学改革研究课题(JXJG-14-2-30)
胡菊菊(1979-),女,博士,副教授,主要从事通信工程专业课程教学与激光混沌的研究工作,E-mail:jxnuhjj@126.com
O441
A
1008-0686(2016)05-0050-03

