原码的阵列乘、除法运算器教学设计
李社蕾,杨婷婷,刘小飞
(三亚学院 理工学院,海南 三亚 572022)
原码的阵列乘、除法运算器教学设计
李社蕾,杨婷婷,刘小飞
(三亚学院 理工学院,海南 三亚 572022)
本文针对“计算机组成原理”课程中阵列乘、除法运算器部分内容,覆盖知识面广,抽象性强等特点,对其课堂组织形式及教学内容安排进行设计,课堂教学实践证明,本教学设计有助于学生对知识点的理解,并将该内容纳入自己的知识体系,有助于学生学习能力的培养。
阵列乘法器;阵列除法器;教学设计
0 引言
“计算机组成原理”是计算机科学与技术及相关专业的核心专业基础课,它一方面以“模拟电路”、“数字逻辑电路”、“汇编语言”等课程为基础,另一方面是“操作系统”、“计算机系统结构”等课程的基础,在课程体系中起着承上启下的作用。学生在学习该课程时,普遍觉得内容抽象、难于理解[1-4]。
为了使学生对计算机基本原理和设计方法有一个清楚的了解,本文针对计算机运算器部分中学生理解困难的原码的阵列乘、除法运算器等内容,就其课堂教学组织及内容安排进行探讨。
1 原码阵列乘法器授课方法研究
课堂上,原码陈列乘法器授课可采用出题、解题和总结的方式进行。例如:三道实例题的授课过程如下:
(1)出一道十进制和一道二进制的乘法题目,让学生在黑板上运算,然后总结,并得出结论:n位数*n位数,乘积最多是2*n位。
(2)针对数字运算出题如式 (1),针对符号运算,出题如式(2):

(1)

(2)
让学生分别写出式(1)的值及式(2)的结果,并启发他们说出各自是什么逻辑,最后总结出:一位二进制乘运算等价于“与”逻辑,符号的运算等价于“异或”逻辑[5-6]。
然后再总结:①十进制乘法运算有100条法则,考虑乘法交换率要背55条。②二进制乘法运算只有4条法则,考虑乘法交换率只要背3条。③定点计算中,两个原码表示的数相乘的运算规则有两条:乘积的符号部分:由两个数的符号位按位异或运算得到;乘积的数值部分:为两个数的数值部分相乘之积。
则乘积为
[z]原=(xf⊕yf)+(xn-1……x1x0)×(yfyn-1…y1y0)
其中,xf为被乘数符号,yf为乘数符号。
(3)在黑板上列出4位二进制小数原码相乘的题目若干,让学生列竖式运算,分析人工算法和机器算法的同异性,如分析4位*4位阵列乘法器的单元结构,如图1所示。

图1 4阵列乘法器的单元结构图
然后对照不带符号的阵列乘法器逻辑电路(图2所示),讲解4位*4位阵列乘法器的工作原理。
此后,学习带求补级的阵列乘法器,先对图3所示的4位求补电路进行分析。

图2 原码阵列乘法器逻辑电路图

图3 4位求补电路
分析过程中,遵照如下规则:
(1)E=0时,输入和输出相等;
(2)E=1时,则从数最右端往左边扫描,直到第一个1出现的时候,该位和右边各位保持不变,左边的各数值位按位取反。
然后,让学生回顾复习负数原码求补码的方法,从而可以得出求补码的另一种方法:从数最右端往左边扫描,直到第一个1出现的时候,该位和右边各位保持不变,左边各数值位按位取反[7]。
然后在4位*4位阵列乘法器逻辑电路图的基础上,增加求补电路即可得到带求补级的4位*4位阵列乘法器逻辑电路图。
2 原码的阵列除法授课方法研究
(1)由中小学的知识可知,除法是乘法运算的逆运算,分析这两种运算涉及到的各数之间的关系,如图4所示:

图4 除法、乘法运算关系图
从而总结出:若被除数为2*n位,除数为n位,则商为n位,余数也是n位。
(2)定点小数除法运算注意之处有两点:
①除数≠0,否则商无穷大,溢出。
②|被除数|<|除数|,无整数商,溢出。
(3)讲解定点小数除法运算法则
设有n位定点小数(定点整数也适用)。
被除数x,其原码为:[x]原=xfxn-1……x1x0。
除数y,其原码为:[y]原=yfyn-1……y1y0。
则有q=x/y,其原码为
[q]原=(xf⊕yf)+(xn-1……x1x0)÷(yfyn-1……y1y0)
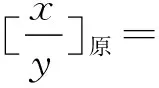
分析:商符:1⊕0=1,商值:提问学生,让学生在黑板上用手工的方法列竖式求之,检查对错,确认无误后,如图5所示,对运算过程进行分析。

图5 手工除法运算
(3)讲解原码恢复与书法运算
商符=1+0=1
商值运算:(先计算除数的补码)


图6 恢复余数除法运算竖式
得商0.101,与商符相拼得1.101,余数为0.000001。
由恢复余数法可得原码的加减交替除法法则[8]:①若够减,商‘1’,右错一位再减;②若够减,商‘1’,右错一位再加。
用原码交替法再做上例:
商符=1+0=1
商值运算:(先计算除数的补码)

图6 加减交替除法运算竖式
故得:商=1.101,余数为0.000001
总结:①若够减,有进位C=1,商‘1’,即q=1,下一步错位再减,即P=1;②若不够减,有进位C=0,商‘0’,即q=0,下一步错位再加,即P=0;
补充介绍可控加法/减法(CAS)单元,如图7所示。
原理:采用不恢复余数(加减交替)法
P=0,作加法运算
P=1,作减法运算

图7 控加法/减法(CAS)单元
综合:P=q=C
q为商,P决定了下一步的运算。P=q=C,即上一步的C值,决定了当前的商和下一步的操作。
在此基础上讲解原码阵列除法器,如图8所示。
不恢复余数的阵列除法器

图8 原码阵列除法器逻辑电路图
被除数 x=0.x6x5x4x3x2x1(双倍长)
除数 y=0.y3y2y1
商数 q=0.q3q2q1
余数 r=0.00r6r5r4r3
在加减交替除法运算中,不再根据余数正负,而是根据最高位有无进位,来决定商和下一步的运算。最后举例让学生用加减交替法进行原码定点除法运算。
4 结语
本文对计算机运算器部分中学生理解困难的阵列乘、除法运算器这部分内容的课堂组织及内容安排进行了教学设计,并将教学内容与学生已有的知识进行衔接,知识点逐步展开,化繁为简,帮助学生将该内容纳入自己的知识体系,本教学设计有助于学生对知识点的理解,有助于学生学习能力的培养。
[1] 李仲生,黄美玲.计算机组成原理与溯源教学法探索_以存储器章节教学为例[J],吉林:考试周刊,2015,71:34,135
[2] 刘芳,戴葵,刘芸,王志英,计算机组成原理中设计性环节的教学探讨[J],北京:计算机教育,2007.4:3-5,8
[3] 黄沛杰,徐东风,殷建军.计算机组成原理实验教学中的计算思维培养[J],北京:计算机教育,2012.8:103-106
[4] 葛方振,刘怀愚,朱昌杰.计算思维与计算机组成原理教学内容设计[J],淮北:淮北师范大学学报(自然科学版),2015.9,36(3):22-25
[5] 江汉.基于Matlab仿真的信道接入协议教学设计[J],南京:电气电子教学学报,37(1)2015.2:63-67,106-110;
[6] 江汉,程云鹏,沈良.EDMA传输机制与系统实时性的教学设计[J],南京:电气电子教学学报, 2015.6,37(3):63-67
[7] 姜欣宁,陈宇.计算机组成原理专题实验_的教学改革[J],北京:实验技术与管理,2013.4,30(4):162-165;
[8] 张磊,郑榕,田军峰.计算机组成原理理论实验教学无缝结合的新方法[J],上海:实验室研究与探索,2013.5,32(5):168-171
The Instructional Design of Original Code Array Multiplication Division Arithmetic Unit
LI She-lei,Yang Ting-ting,LIU Xiao-fei
(ScienceandEngineeringDepartment,SanyaCollege,Sanya572022,China)
According to the characteristics of broad scope and abstraction for array multiplier and arrays divider in the Computer Organization Principles course, the new ways of classroom organization and arrangement of teaching content is designed, classroom teaching activities has proved that this teaching design is helpful to students understanding of knowledge points, and bring the content into their own knowledge system, and cultured learning ability of students.
array multiplier; array divider; instructional design
2015-11-19;
2016-05-05
李社蕾(1979-),女,讲师,主要从事计算机科学与技术专业的教学工作,E-mail:lishelei@126.com
G642
A
1008-0686(2016)06-0097-04

