蝶形电阻网络圆周边界任意端口间等效电阻的计算
胡菊菊,王一凡,嵇英华
(江西师范大学 物理通信电子学院,江西 南昌 330022)
蝶形电阻网络圆周边界任意端口间等效电阻的计算
胡菊菊,王一凡,嵇英华
(江西师范大学 物理通信电子学院,江西 南昌 330022)
本文将电路理论中的网孔分析法与递归变换法相结合,给出了一种求解蝶形电阻网络圆周边界任意端口间等效电阻的简捷方法。计算过程中,首先基于网孔分析法建立了非线性的差分方程组,随后利用矩阵变换方法,将非线性差分方程组转化为线性的差分方程组。此外,本文将一般外加单一电流源求等效电阻的策略推广为外加多个电流源,由此获得的等效电阻解析表达式可适用于计算任意端口的等效电阻。
递归-变换;蝶形网络;等效电阻
0 引言
最近十年来,不仅几种典型梯形电阻网络等效电阻的计算受到人们较大的关注,而且蝶形电阻网络等效电阻的计算也日益受到重视[1-3]。 文献[4]应用递归变换法,初步研究了蝶形电阻网络的径向等效电阻。显然,人们还常常需要知道如图1所示的蝶形电阻网络沿圆周边界任意两个端点间的等效电阻。为此,本文在文献[4]的基础上,将电路理论中的网孔分析法与递归变换法相结合,给出了计算蝶形电阻网络圆周边界任意端口间等效电阻的一种简捷方法。
1 模型与网孔电流方程
为说明问题简捷起见,本文先详细计算图1所示的5×N阶蝶形电阻网络圆周边界任意端口间等效电阻,再给出一般的推广表达式。
图1中各节点的标示规则为:沿圆周按顺时针方向,标示为Ak(k=0,1,2…,N-1);沿径向由中心向边缘,标示为Bm(m=1,2,…,5)。 网孔电流由内向外标示为imk,方向均取为顺时针。在图1中,径向电阻的阻值均为r0,外边界圆周方向电阻的阻值为2r,其他圆周方向电阻的阻值均为r。为给出端口处的电流-电压关系,沿着圆周边界,在相邻输入端点间施加电流源。如图2所示,外加电流源分别为isn(n=1,2,…,N)。
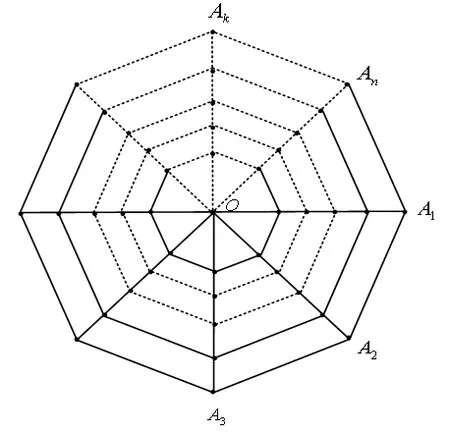
图1 5×N阶蝶形电阻网络
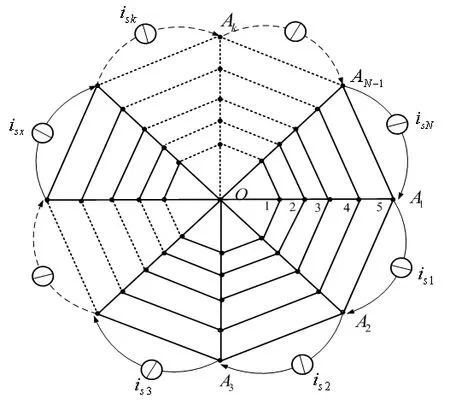
图2 外加电流源法计算蝶形电阻网络端口的等效电阻
无外加电流源作用时,选择第k列的5个独立网孔,应用网孔分析法列出如下网孔电流矩阵方程
Ik+1=CIk-Ik-1
(1)
式(1)中网孔电流矩阵定义为
Ik=(i1ki2ki3ki4ki5k)T
(2)
无量纲的5×5参数矩阵C则为(a=r/r0)
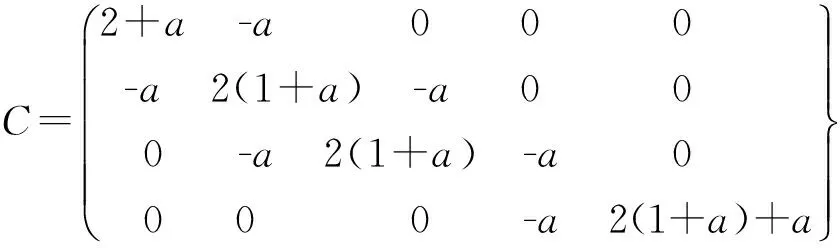
(3)
2 矩阵变换
式(1)为一个非线性的差分方程,可以应用文献[5]给出的递归—变换法求解.设参数矩阵C的本征值为λm(m=1,2,…,5), 满足如下的久期方程
det|C-λmE|=0
(4)
E为单位矩阵.引入一个5×5的满足如下约束方程的变换矩阵S
SCS-1=diag(λ1λ2λ3λ4λ5)
(5)
根据式(3)与(4),在r0=r的情形下,对约束方程式(5)直接计算后可得变换矩阵S为
(6)
(7)
对应于参数矩阵C的本征值λm为
λm=2+2a(1-cosθm)
(8)
将变换矩阵S作用于式(1)两边,并结合式(5),式(1)将变换成:
Yk+1=TYk-Yk-1
(9)
(10)
式(9)实际上描述了如下五个独立的线性差分方程:
(11)
m=1,2,…,5,设αm与βm是式(11)对应的特征方程
(12)
的特征根,不难得到
αm=1+α(1-cosθm)+A
(13)
βm=1+α(1-cosθm)-A
(14)
基于递归法,第k列相应的广义网孔电流的解析表达式为
(15a)
k=1,2,…,N,其中
(15b)
3 边界条件
为了计算任意两个端点间的等效电阻,下面需要考虑外加电流源的作用以及边界条件。考虑到蝶形网络的周期性,故不失一般性,总可以设p=0,q=x(0≤x≤N)。具体计算方法是:如果我们需要计算A0-Ax端点间的等效电阻,则令A0-Ax间的外加电流源都等于一个不为零的常数iS,不在A0-Ax间的外加电流源则取值为零,即
(16)
从等效的角度,该式等效于将一个外加电流源 施加于端点A0-Ax之间。在外加电流源的作用下,递推关系式(14)必须修改为如下的分段递推关系
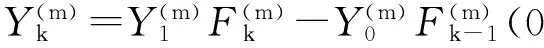
(17)
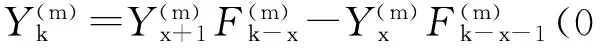
(18)
对于k=0,x的边界点,应用前面完全相同的推导步骤,可得
Y1+YN-1=TY0-aSIS0
(19)
Yx+1+Yx-1=TYk-aSIsk
(20)
其中
IS0=ISx=(is0 0 0 0)T
(21)
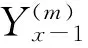
(22)
(23)
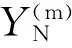
(24)
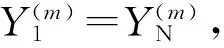
(25)
联立求解式(22)-式(25),可以得到

(26)
(27)

4 蝶形电阻网络端口处的等效电阻
由式(3)与式(14),不难得到
(28)
ST表示矩阵S的转置矩阵,即有
(29)
由此,通过圆周外边界(m=5)各个电阻上的电流则为
ik=i5k-is
(30)
则A0-Ax端点间的等效电阻Rx为
(31)
这正是文献[4]应用支路电流法得到的等效电阻猜想解析表达式。
事实上,我们可以很方便地将式(31)推广至计算M×N阶蝶形电阻网络圆周边界端点间的等效电阻.具体做法如下:将图1与图2分别扩展为M×N阶蝶形电阻网络,选择第k列的M个独立网孔,应用网孔分析法列出网孔电流方程。对于M×N阶蝶形电阻网络,式(6)中的变换矩阵S应修改为
(32)
(33)
基于式(32)与式(33),采用与前面完全相同的推导变换,对于 阶蝶形电阻网络,即有
(34)
(参见文献[6])
5 结语
本文以 阶蝶形电阻网络为例,将电路分析中的网孔分析法与组合数学中的递归变换法相结合,严格推导了蝶形电阻网络圆周边界任意端口间等效电阻,给出了等效电阻通用的解析表达式。计算过程中,首先基于网孔分析法建立了非线性的差分方程组,随后利用矩阵变换方法,将非线性的差分方程组转化为线性的差分方程组。整个求解过程思路简捷清晰,计算程序规范。
(胡菊菊等文)
[1] J.W.Essam, F.Y.Wu.The exact evaluation of the corner-to-corner resistance of an M×N resistor network:asymptotic expansion [J].J.Phys.A:Math.Theor., 2009, 42 1-10.
[2] J.W.Essam, Z.Z.Tan, F.Y.Wu.Resistance between two nodes in general position on an m×n fan network [J] Phys.Rev.E 90, 2014, 032130.
[3] Z.Z.Tan, L.Zhou, J.H.Yang.The equivalent resistance of a 3×n cobweb network and its conjecture of an m×n cobweb network [J].J.Phys.A:Math.Theor., 2013, 46 195202.
[4] Z.Z.Tan, J.H.Fang.Two-point resistance of a cobweb network with a 2r boundary [J].Commun.Theor.Phys., 2015, 63 36-44.
[5] Z.Z.Tan.Recursion-transform method for computing resistance of the complex resistor network with three arbitrary boundaries [J].Phys.Rev.E 91, 2015, 052122.
[6] Z.Z.Tan, L.Zhou, D.F.Luo.Resistance and capacitance of 4×n cobweb network and two conjectures [J].Int.J.Circ.Theor.Appl., 2015, 43 329-341.
Equivalent Resistance Between Arbitrary Ports on the Circle Boundary in the Butterfly Resistance Network
HU Ju-ju, WANG Yi-fan, JI Ying-hua
(CollegeofPhysicsandCommunicationElectronics,JiangxiNormalUniversity,Nanchang330022,China)
This paper proposes a simple method for equivalent resistance between arbitrary ports on the circle boundary in the butterfly resistance network by the mesh analysis in circuit theory and the recursion-transformation in combination mathematics.During the calculations, nonlinear difference equations are firstly built based on mesh analysis, and then matrix transformation is used to transform the nonlinear difference equations to linear equations.Furthermore, singlet current source is extended to multiple current sources to solve equivalent resistance, the obtained analytic expressions apply to the equivalent resistance between arbitrary ports.
recursion-transformation; butterfly network; equivalent resistance
2016-01-28;
2016-04-15 基金项目::江西省高等学校教学改革研究课题资助(课题编号:JXJG-14-2-30)
胡菊菊(1979-),女,博士,副教授,主要从事通信工程专业课程教学与激光混沌的研究工作,E-mail:jxnuhjj@126.com
O441
A
1008-0686(2016)06-0074-04

