温度荷载作用下高速铁路无砟轨道伤损反演分析
温度荷载作用下高速铁路无砟轨道伤损反演分析
周洋,向俊,余翠英,曹立
(中南大学 土木工程学院,湖南 长沙 410075)
高速铁路无砟轨道结构的轨下基础主要为混凝土结构,而混凝土结构对温度荷载比较敏感,在温度荷载长期作用下,可能会导致结构的疲劳伤损,乃至开裂,将直接影响结构耐久性,严重时影响其承载力及行车安全。目前,针对无砟轨道结构伤损成因分析及工程处置措施等方面的研究文献相对较多。而对无砟轨道结构伤损从萌发、出现、发展、直至最后的宏观表现的整个过程的描述,换言之,对无砟轨道结构伤损的反演分析则鲜见报道。伤损反演分析是从一个新的角度重现伤损产生及发展过程,既属于机理探讨,又属于有限元仿真试验模拟。然而,基于传统的弹性本构关系,无论应力如何变化,也无法在模型中反映出这种伤损,在外力得到释放后,结构会恢复到原有的状态。因此必须采用混凝土塑性本构模型来解决这一问题。塑性损伤模型与经典弹性损伤模型及弹塑性模型一样,是一种对混凝土宏观受力现象的抽象,并将这种缺陷带来的破坏转化为塑性应变,是一种将混凝土压碎或者裂缝宽度以应变的方式“弥散”到混凝土单元中的模型,并将其抽象成“应力—应变—伤损”本构模型[1-2]。从塑性损伤模型提出伊始,国内外学者已进行了大量研究。在材料领域,学者们根据大量的实验数据统计出了各种混凝土本构模型,也提出了一些伤损因子的计算方法,并与实验数据有较好的吻合[3-4];在结构领域,学者们也已成功地将该模型与有限元法相结合,并应用于实际问题[5];在高速铁路领域,亦有研究者对塑性损伤本构进行了相关研究,只是初步模拟了在重复列车荷载作用下可能导致的结构疲劳破坏[6-8]。Abaqus软件中的Concrete Damage Plastic(CDP)模块,是基于Lubliner等[9]的理论,采用各向同性的刚度退化来替代混凝土非弹性行为的。本文拟采用Abaqus中的CDP模块,通过输入混凝土塑性损伤本构关系,模拟CRTS-I型板式无砟轨道混凝土部件(以轨道板为例)在温度荷载作用下的伤损过程,通过此种反演模拟,再现无砟轨道混凝土部件伤损产生过程及变化规律,对于无砟轨道设计、施工及养护维修具有一定理论指导作用。

1塑性损伤本构关系
1.1应力应变本构关系的修正
本文采用塑性损伤本构关系,模拟CRTS-I型板式轨道结构轨道板的损伤过程。由于轨道板采用的是C60高强混凝土材料,借鉴材料及结构领域中针对高强混凝土的相关研究成果[3-4],采用如下应力应变本构关系。
受拉本构关系见式(1)。
(1)

受压本构关系见式(2)。
(2)

由于在使用Abaqus的CDP模块过程中,在应力应变本构关系中需要提供一个弹性段,否则,无法输入此本构关系,而式(1)与(2)中无弹性段,因此,需对其进行修改。本文采用文献[5]中的受压本构峰值点割线反推受压本构弹性极限点的方法,具体修改结果如下。
修正后的割线弹性模量见式(3)。
(3)
修正后的受拉本构关系见式(4)。
(4)
修正后的受压本构关系见式(5)。
(5)
1.2非弹性应变和损伤因子的计算
因为Abaqus软件中是按照“应力—非弹性应变—损伤因子”关系来输入本构模型的,所以需要将常用的“应力—应变—损伤因子”关系进行转化。
Abaqus提供的应变和非弹性应变的关系如图1所示。
(6)
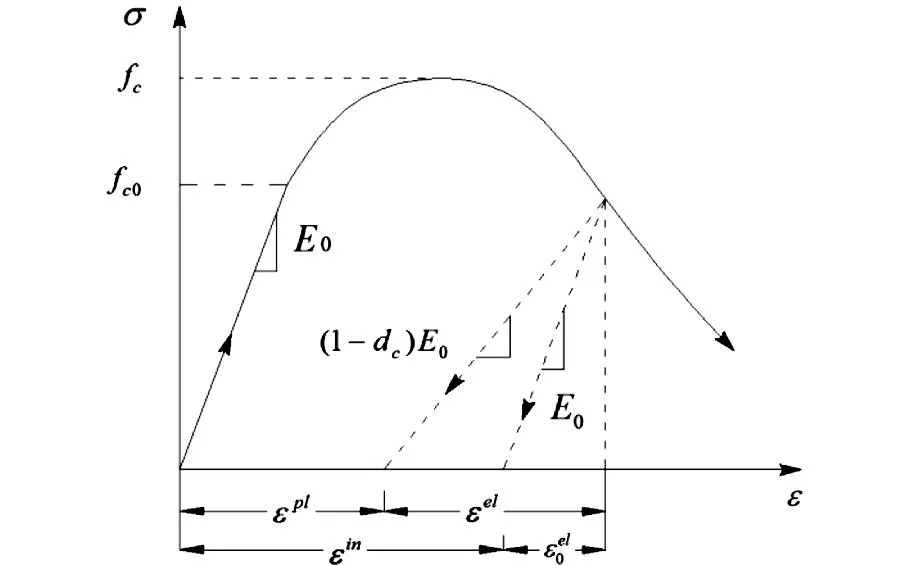
图1 Abaqus中混凝土刚度退化Fig.1 Stiffness degradation of concrete in Abaqus
根据Najar[12]的能量等效理论和文献[13-14],伤损因子为阴影部分面积与虚线三角形面积的比值,如图2所示。

图2 损伤因子计算方法示意图Fig.2 Schematic diagram about damage parameter calculation
则损伤因子计算为
(7)
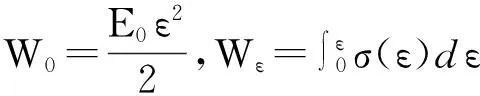
由于Abaqus的CDP模块中,混凝土本构模型是采用散点模式输入的,并且由Abaqus自行完成插值拟合。因此需要在修正后的本构曲线中进行取样,选取合适的散点以后,输入Abaqus的CDP模块中,最终可以确定轨道板混凝土塑性损伤本构关系。为了便于读者阅读与应用,本文列出具体输入散点见表1与表2。
表1C60高强混凝土受压塑性损伤本构离散值
Table 1 Discrete data of compressive plastic damage constructive model of C60 high strength concrete

σ/MPaεind45.0276040047.4668900.00021550.01559521745.2457360.00048180.04246944130.3294390.00153260.18361426519.9212430.00240630.33774677715.0821370.00297160.43960919410.0849310.00386230.5788618864.00907860.00689920.824096692.40524680.00985440.905401919
表2C60高强混凝土受拉塑性损伤本构离散值
Table 2 Discrete data of tensile plastic damage constructive model of C60 high strength concrete
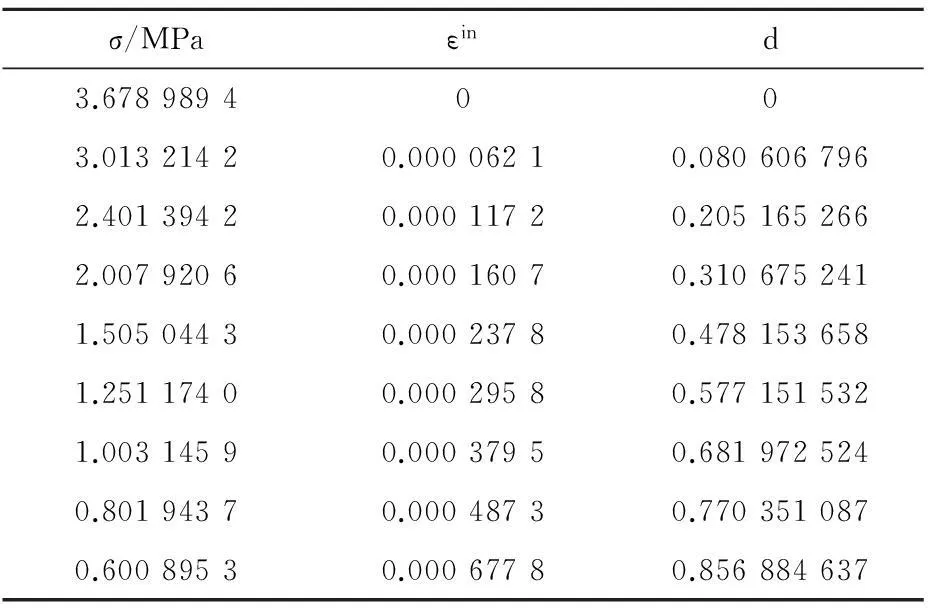
σ/MPaεind3.6789894003.01321420.00006210.0806067962.40139420.00011720.2051652662.00792060.00016070.3106752411.50504430.00023780.4781536581.25117400.00029580.5771515321.00314590.00037950.6819725240.80194370.00048730.7703510870.60089530.00067780.856884637
2计算模型与方法
2.1计算模型
基于Abaqus软件建立的CRTS-I型单元板式轨道有限元计算模型如图3所示,有关图3的具体说明如下。

图3 CRTS-I型单元板式轨道1/4部分有限元模型Fig.3 1/4 finite element model of CRTS-I slab track
由于本文只考虑温度荷载作用,不考虑列车的作用,所以对钢轨部件进行适当简化,将一个相邻扣件长度的钢轨按照重力荷载施加给扣件(模拟为弹簧);基于无缝线路的特点,约束扣件顶部节点的纵向自由度,同时扣件底部节点耦合于垫板顶面受力区域;因本文只针对轨道板的伤损反演分析,未考虑乳化沥青水泥砂浆(以下简称砂浆层)和底座板的损伤演化,故忽略其重力荷载,并将其视为传统的弹性材料;因本文只考虑温度荷载作用,未考虑不均匀沉降荷载的作用,视基础为刚性材料,并完全固定底座板底面三向自由度;鉴于CRTS-I型单元板式轨道结构的对称性,只取如图3所示的一个单元板式轨道结构的1/4部分模型,并约束单元板边界在线路方向的自由度,同时,约束2个轴对称面的法向自由度,以模拟边界条件。
由于在Abaqus中,伤损因子是根据真实应变结果进行返回的[15],因此,应力应变塑性损伤本构关系在用于有限元计算时,存在较大的网格精度敏感性。为此,须对轨道板网格划分方案进行试算,特别是在产生较大伤损的部分进行网格优化。如图3所示,须加密承轨台、预应力钢筋卯穴和限位孔附近的网格。此外,尚须考虑钢筋的影响,所有预应力钢筋和普通钢筋均按照设计状态在轨道板中予以考虑。
2.2计算参数
采用Abaqus计算所需的且与图3有关的基本材料属性参数见表3,表3中ρ表示密度;E表示弹性模量;λ表示泊松比;α表示线膨胀系数;kz表示钢轨扣件竖向刚度;ky表示钢轨扣件横向刚度。

表3 材料属性参数表
2.3温度荷载
文献[16]对现场轨道板上、下表面温度之差随时间变化关系进行了连续跟踪测试,统计结果如图4所示。图4中的纵轴表示轨道板上、下表面温度差,横轴表示1 d 24 h。具体温度荷载是以温度梯度(图4中的相应纵坐标除以轨道板厚度)的方式施加于轨道板中。需要说明的是,实际情况中,温度变化属于持久缓慢的加载荷载,这种持续加载会使得结构伤损充分扩展,从而使得计算模型无法完全等同材料实际模型,因此,计算中的一次加载不可以等效为实际中的1 d荷载[17]。本文中的加载次数即为图4重复次数。

图4 轨道板顶面与底面温度之差随时间变化关系Fig.4 Relationship of time and temperature difference between top and bottom of slab
荷载施加方法说明如下:
第1步,施加钢筋预应力荷载、轨道板重力荷载及钢轨重力荷载。
第2步,初始化温度荷载。为了增加收敛速度,不能直接从0摄氏度直接进行加载,否则会导致计算不收敛。因此,首先应当提供一个从0变化到第1次循环荷载初始状态的过程,按照图4提供1次0~8 ℃的温度施加过程。
第3步,循环施加温度荷载。根据图4对轨道板施加循环温度荷载,总计1 000次,并分别提取50,200,400,600,800及1 000次时的计算结果,供轨道板伤损过程反演分析之用。
3计算结果与分析
基于上述塑性损伤本构关系、计算模型及方法,在温度荷载循环作用下,对CRTS-I型板式无砟轨道结构轨道板部件伤损产生过程进行了计算。由于受篇幅限制,本文仅罗列了几组具有代表性的温度循环荷载(50,200,400,600,800及1000次)作用下,轨道板产生的最大主塑性应变云图,分别如图5~图10所示,在每一组图中,(a)为整体塑性应变云图,(b)为沿横向卯穴上缘截面的塑性应变云图。
由于模型中的塑性应变是一种将裂缝宽度平均到混凝土某局部区域的一种抽象表示,因此,塑性应变可以反映损伤[2]。基于此种观点,本文认为塑性拉应变可视为开裂,而塑性压应变则可视为压碎;考虑到塑性应变对伤损的反映特性、混凝土材料的不均匀性及其它因素,本文计算结果中的伤损位置,实际是一个局部区域,而非精准位置;本文以是否出现塑性拉应变作为轨道板是否损伤的判定基准。

(a)整体塑性应变云图;(b)横向卯穴上缘截面的塑性应变云图图5 温度荷载循环作用50次时,轨道板中最大主塑性应变云图Fig.5 Max principle plastic strain of slab under 50 times temperature loads
需要说明的是:1)在图5~图10的云图中,由白色逐渐变化到黑色的过程对应塑性应变由低到高的变化过程;2)鉴于轨道板中钢筋与混凝土界面薄弱性,为了直观表达,专门列示了钢筋横向卯穴上缘截面处的塑性应变云图;3)由图5~图10可见,伤损首先会在某些特定区域集中产生,其伤损程度随着荷载的累计将不断加深,例如,纵向钢筋卯穴上表面的拉伤,从小块的伤损,不断劣化,发展至大的拉伤区域。
图5表示温度荷载累积循环50次时,轨道板中出现的最大主塑性应变云图。图中,除了钢筋卯穴周围已经出现了2×10-4数量级的塑性拉应变,总体塑性应变呈受压损伤,由于混凝土是一种相对抗压的材料,因此,可以认为仍然处于低损伤状态或者是无损伤状态。这种卯穴周围的损伤来源主要是预应力钢筋,特别是锚具,给轨道板结构局部带来了一个初始损伤。

(a)整体塑性应变云图;(b)横向卯穴上缘截面的塑性应变云图图6 温度荷载循环作用200次时,轨道板中最大主塑性应变云图Fig.6 Max principle plastic strain of slab under 200 times temperature loads
图6表示温度荷载循环200次时,轨道板中出现的最大主塑性应变云图。图中,最大塑性拉应变为5.838×10-4,虽然与图5中温度荷载循环50时的结果基本相近,但是,在区域上有了比较明显的扩展;除了钢筋卯穴周围,没有明显可见的受拉区域;在承轨台下方,处于1×10-4数量级的塑性拉应变表明,此处已经有了明显可见的伤损区域;在限位孔处,出现了受压塑性应变。

(a)整体塑性应变云图;(b)横向卯穴上缘截面的塑性应变云图图7 温度荷载循环作用400次时,轨道板中最大主塑性应变云图Fig.7 Max principle plastic strain of slab under 400 times temperature loads
图7表示温度荷载循环400次时,轨道板中出现的最大主塑性应变云图。图中,最大塑性拉应变为6.607×10-4,相对图6而言,不管是量值,还是塑性应变产生区域,有增大趋势;在承轨台下方,处于2×10-4数量级的塑性拉应变,有了明显可见的区域,而且,还出现了4×10-4数量级的塑性拉应变区域;钢筋卯穴上缘部分,相对图6来说,出现的塑性应变区域没有较大变化,然而,处于4×10-4数量级的塑性拉应变,亦有了明显可见的区域;在限位孔处,出现的塑性应变向内扩展,但仍然处于受压塑性损伤。
图8表示温度荷载循环600次时,轨道板中出现的最大主塑性应变云图。图中,最大塑性拉应变为7.785×10-4,相对图7而言,不管是量值,还是塑性应变产生区域,有增大趋势,但不够明显;在承轨台下方,处于4×10-4数量级的塑性拉应变已经有了明显可见的区域,而且,还出现了5×10-4数量级的塑性拉应变区域;在钢筋卯穴上缘部分,处于4×10-4数量级的塑性拉应变已经有了明显可见的区域,卯穴周围的塑性应变区域开始明显地向内扩展,卯穴与卯穴之间贴近轨道板顶面部分出现了贯通伤损塑性应变区域;在限位孔处,相对图7而言,出现的塑性应变有向上扩展的趋势,原本出现的塑性压应变,逐渐发展成了塑性拉应变。
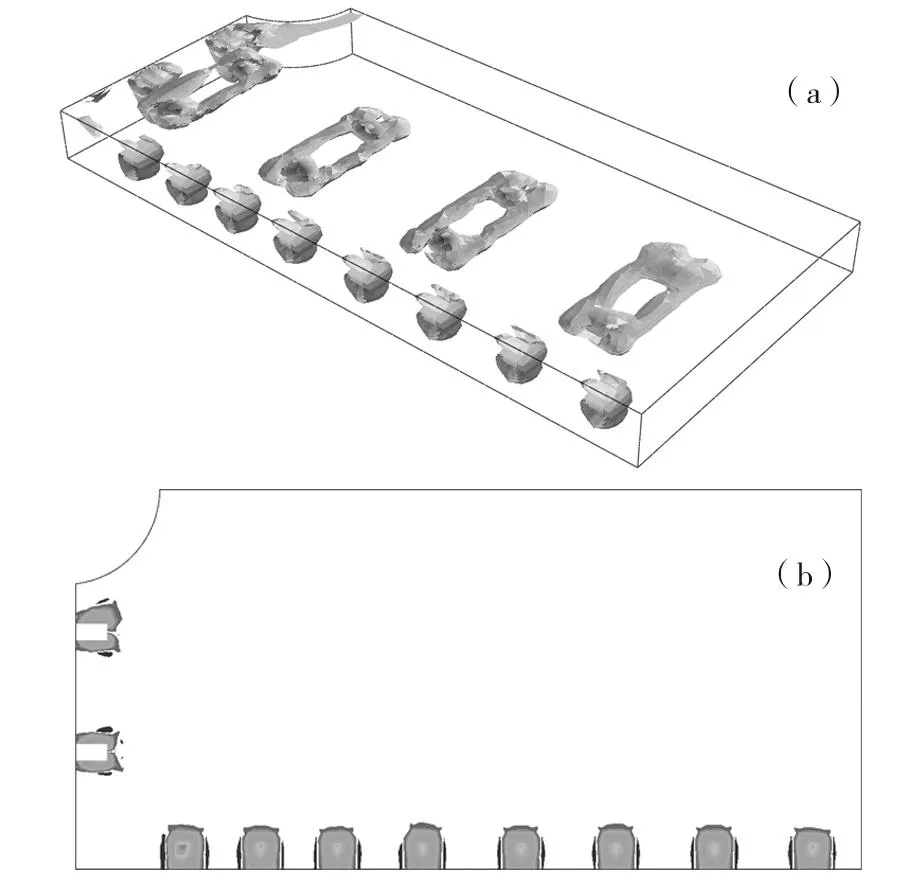
(a)整体塑性应变云图;(b)横向卯穴上缘截面的塑性应变云图图8 温度荷载循环作用600次时,轨道板中最大主塑性应变云图Fig.8 Max principle plastic strain of slab under 600 times temperature loads

(a)整体塑性应变云图;(b)横向卯穴上缘截面的塑性应变云图图9 温度荷载循环作用800次时,轨道板中最大主塑性应变云图Fig.9 Max principle plastic strain of slab under 800 times temperature loads
图9表示温度荷载循环800次时,轨道板中出现的最大主塑性应变云图。图中,最大塑性拉应变为8.844×10-4,处于6×10-4数量级的塑性受拉区域已经有了明显的集中;在承轨台下方,处于4×10-4数量级的塑性拉应变,已经有了明显可见的区域,而且,出现了6×10-4数量级的塑性拉应变区域,不但在量值上还是区域上,都有明显增大趋势;在卯穴上缘部分,相对图8而言,卯穴与卯穴之间贴近轨道板顶面部分的贯通塑性应变区域明显扩大;在限位孔处,塑性应变区域继续扩大,并且扩展到了轨道板顶面。

(a)整体塑性应变云图;(b)横向卯穴上缘截面的塑性应变云图图10 温度荷载循环作用1000次时,轨道板中最大主塑性应变云图Fig.10 Max principle plastic strain of slab under 1000 times temperature loads
图10表示温度荷载循环1000次时,轨道板中出现的最大主塑性应变云图。图中,最大塑性拉应达到了1.032×10-4;在承轨台下方,处于6×10-4数量级的塑性拉应变已经有了明显可见的区域,四个承轨台下方区域呈现较严重的伤损现象;在卯穴上缘部分,伤损亦表现为较严重,所有区域出现了6×10-4数量级的塑性拉应变,塑性应变区域向内扩展非常显著;在限位孔处,塑性应变区域已经与纵向钢筋卯穴周围区域以及第一个承轨台下方区域完全贯通。
综上所述,可以得出如下几点印象和规律:
1)采用本文建立的模型及参数,可以一次性地把握住轨道板在温度荷载作用下的伤损大致区域,这些伤损区域与CRTS-I型板式无砟轨道服役状态是一致的。例如,现场已发现大量的轨道板钢筋卯穴处开裂、轨道板在承轨台附近的开裂、凸型挡台周围限位孔处开裂等等。
2)在温度荷载作用初期阶段,轨道板伤损出现的区域很小,尤其是程度很轻,而且变化缓慢。当温度荷载循环次数累积到一定程度时,随着循环次数的增加,轨道板伤损区域扩展明显,程度增加显著,而且伤损变化加快。
3)随着温度荷载循环次数的不断累积,轨道板出现的一些局部伤损有贯通趋势。
4)对于CRTS-I型板式无砟轨道结构轨道板而言,不管是设计、施工,还是养护维修,应重点关注钢筋卯穴、凸型挡台周围限位孔及承轨台下方等容易出现伤损的薄弱处所,积极采取应对措施,将伤损降低到最低限度,确保结构及行车安全。
4结论
1)轨道板可能出现温度伤损主要出现在:承轨台向下延伸区,钢筋卯穴边缘纵向狭窄区及限位孔周围轨道板上层区。
2)处于承轨台区域的温度伤损,主要表现为由承轨台周边向下扩展。处于钢筋卯穴处的温度伤损,则存在2种表现状况,一是由卯穴逐步向内部扩展,二是伤损在卯穴间的贯通。处于限位孔区域的温度伤损,主要表现为从中间向上方扩展,并且易与纵向钢筋卯穴周围及第1个承轨台下方伤损贯通。
参考文献:
[1] 江见鲸. 钢筋混凝土结构非线性有限元分析[M]. 西安:陕西科学技术出版社,1994.
JIANG Jianjing. Finite element techniques for static analysis of structures in reinforced concrete[M]. Xi’an: Shanxi Science and Technology Press,1994.
[2] 于海祥. 基于理想无损状态的混凝土弹塑性损伤本构模型研究及应用[D].重庆:重庆大学,2009.
YU Haixiang. Research and application on elastoplastic damage constitutive model for concrete based on ideally undamaged state[D]. Chongqing: Chongqing University, 2009.
[3] 丁发兴,余志武. 混凝土受拉力学性能统一计算方法[J]. 华中科技大学学报(城市科学版),2004,21(3):29-34.
DING Faxing, YU Zhiwu. Unified calculation method of mechanical properties of concrete in tension[J]. Journal of Huazhong University of Science and Technology (Urban Science Edition),2004,21(3):29-34.
[4] 余志武,丁发兴. 混凝土受压力学性能统一计算方法[J]. 建筑结构学报,2003, 24(4): 41-46.
YU Zhiwu, DING Faxing. Unified calculation method of compressive mechanical properties of concrete[J]. Journal of Building Structures,2003,24(4): 41-46.
[5] 张劲,王庆扬,胡守营,等. ABAQUS混凝土损伤塑性模型参数验证[J]. 建筑结构, 2008,38(8):127-130.
ZHANG Jin, WANG Qingyang, HU Shouying, et al. Parameters verification of concrete damaged plastic model of ABAQUS[J]. Building Structure,2008, 38(8): 127-130.
[6] 蔡成标,朱胜阳,刘秀波,等.高速铁路无砟轨道疲劳检算轮载的动力学分析[J]. 中国科学:技术科学,2014,44(7):707-713.
CAI Chengbiao, ZHU Shengyang, LIU Xiubo, et al. Dynamic analysis of fatigue check load for ballastless track in high-speed railway[J]. Scientia Sinica Technologica,2014,44(7):707-713.
[7] ZHU Shengyang, FU Qiang, CAI Chengbiao, et al. Behavior and performance of ballastless track with damaged cracks under train load. Proceedings of the 2010 International Conference of Logistics Engineering and Management[C]//New York: American Society of Civil Engineers, 2010(387):1518-1524.
[8] 朱胜阳,蔡成标. 一种高速铁路无砟轨道混凝土结构疲劳伤损模型[J]. 中国科学:技术科学,2014,44(7):714-721.
ZHU Shengyang, CAI Chengbiao. A fatigue damage model of concrete structure for ballastless track in high-speed railway[J]. Scientia Sinica Technologica, 2014,44(7):714-721.
[9] 朱胜阳,蔡成标. 温度和列车动荷载作用下双块式无砟轨道道床板伤损特性研究[J]. 中国铁道科学,2012,33(1):6-12.
ZHU Shengyang, CAI Chengbiao. Research on the damage characteristics of double-block ballastless track bed slab under temperature and vehicle dynamic loads[J]. China Railway Science,2012,33(1): 6-12.
[10] Lubliner J, Oliver J, Oller S, et al. A plastic-damage model for concrete[J]. International Journal of Solids and Structures, 1989, 25(3): 299-326.
[11] Dassault. Damaged plasticity model for concrete and other quasi-brittle materials[DB/OL]. http://xn-90ajn.xn-p1ai:2080/ v6.12/books/stm/default.htm.
[12] Krajcinovic D, Fonseka G U. The continuous damage theory of brittle materials,Part 1: General Theory[J]. Journal of Applied Mechanics,1981,48(4): 809-815.
[13] 丁发兴,余志武,欧进萍. 混凝土单轴受力伤损本构模型[J]. 长安大学学报(自然科学版),2008,28(4):70-73.
DING Faxing, YU Zhiwu, OU Jinping. Damage constitutive model for concrete under uniaxial stress conditions[J]. Journal of Chang’an University (Natural Science Edition),2008,28(4):70-73.
[14] 秦浩,赵宪忠. ABAQUS混凝土伤损因子取值方法研究[J]. 结构工程师,2013, 29(6):27-32.
QIN Hao, ZHAO Xianzhong. Study on the ABAQUS damage parameter in the concrete damage plasticity model[J]. Structural Engineers,2013,29(6):27-32.
[15] 聂建国,王宇航. ABAQUS中混凝土本构模型用于模拟结构静力行为的比较研究[J]. 工程力学,2013,30(4):59-67.
NIE Jianguo, WANG Yuhang. Comparison study of constitutive model of concrete in ABAQUS for static analysis of structures[J]. Engineering Mechanics, 2013,30(4):59-67.
[16] 刘钰,陈攀,赵国堂. CRTSⅡ型板式无砟轨道结构早期温度场特征研究[J]. 中国铁道科学,2014,25(1):1-6.
LIU Yu, CHENG Pan, ZHAO Guotang. Study on the characteristics of early temperature field of CRTSⅡ slab ballastless track structure[J]. China Railway Science,2014,25(1):1-6.
[17] 库马梅塔, 保罗蒙特罗. 混凝土:微结构、性能和材料[M]. 覃维祖等,译.北京:中国电力出版社, 2008.
Kumar Mehta P, Moneteiro Paulo J M. Concrete: Microstructure, properties and materials[M]. QIN Weizu, Tran. Beijing: China Electric Power Press, 2008.
(编辑阳丽霞)
摘要:基于混凝土塑性损伤模型,采用Abaqus软件,以CRTS-I型板式无砟轨道为例,对温度荷载长期作用下结构伤损产生的全过程进行计算机反演模拟,以重现伤损产生的过程及变化规律。计算结果表明:在温度荷载重复作用下,CRTS-I型板式无砟轨道首先会在钢筋卯穴、承轨台及限位孔等处所及其周边出现伤损;随着温度荷载循环次数的累积,钢筋卯穴处伤损将向内部扩展并加深,承轨台处伤损将向周围和下方扩展并加深,限位孔处伤损将向其周围扩展并加深;上述计算机反演结果与现场实际情况基本一致。本文方法与结果对施工及养护维修具有一定理论指导作用。
关键词:铁道工程;高速铁路;无砟轨道;温度荷载;塑性伤损;反演
Inversion analysis of damage of ballastless track in high-speed railway under temperature loadsZHOU Yang, XIANG Jun, YU Cuiying, CAO Li
(School of Civil Engineering, Central South University, Changsha 410075, China)
Abstract:Based on concrete damaged plasticity model in Abaqus, this paper simulates the process of long-term temperature load damage of CRTS-I type slab ballastless track. Simulation result shows that under the cycling temperature load, damage first appears around rebar anchors, convexes and under the fasteners. With the cycles are accumulated, the damage is expanded and deepened. The computer inversion phenomenon fits the result in-site. The method and results could be the guidance for construction and maintenance.
Key words:railway engineering; high-speed railway; ballastless track; temperature load; damage; inversion
中图分类号:U213.2
文献标志码:A
文章编号:1672-7029(2016)01-0001-08
通讯作者:向俊(1968-),男,湖南溆浦人,教授,博士,从事列车脱轨控制工程,列车-轨道(桥梁)系统振动及轨道力学研究;E-mail: jxiang@csu.edu.cn
基金项目:国家自然科学基金委员会与神华集团有限公司联合资助项目(U1261113);高等学校博士学科点专项科研基金项目(20100162110022);牵引动力国家重点实验室开放课题资助项目(TPL1214,TPL0901);江西省青年科学基金资助项目(20142BAB216003)
收稿日期:*2015-06-25

