基于同站台换乘的高铁车站作业计划优化编制
基于同站台换乘的高铁车站作业计划优化编制
赵茜芮1,2,张琦2
(1.北京交通大学 轨道交通控制与安全国家重点实验室,北京 100044;
2.北京交通大学 交通运输学院,北京 100044)
摘要:针对基于同站台换乘的高速铁路车站作业计划优化编制问题展开研究,基于咽喉区进路与到发线一体化优化的原则,以最小化到发线运用的不均衡性及最大化同站台换乘满足的潜在客流量为目标,建立高速铁路车站作业计划优化编制的多目标0-1整数规划模型,并采用遗传算法求解,通过广义进路概念的引入,提高算法的搜索效率,最后以武汉站高速场的实例验证了模型与算法的有效性。
关键词:高速铁路;车站作业计划;同站台换乘;遗传算法
随着高速铁路的成网运营,客流量逐步增长、路网结构趋于复杂,仅仅依靠直达的运输组织模式无法适应高速铁路的成网运营情况,需要中转换乘模式与直达模式的配合共同完成路网上客流的输送。同站台换乘作为一种便捷的中转换乘方式能够保障换乘客流的服务质量,而同站台换乘的实现有赖于高速铁路车站作业计划的合理编制,通过为列车安排合理的到发线完成列车之间有效的换乘接续。因此,本文针对考虑同站台换乘情况下的高速铁路车站作业计划优化编制问题展开研究。高速铁路车站作业计划的编制是指以列车运行图、动车组运用计划、车站技术作业时间标准与车站平面图作为输入条件,为列车安排咽喉区进路占用方案和到发线运用方案的过程。根据车站作业计划的优化编制是否考虑咽喉区进路的决策选择分为2类:第一,若不考虑咽喉区进路的决策选择,则是到发线运用计划的优化编制,Billionnet等[1-10]针对到发线运用计划的优化编制展开研究;第二,若考虑咽喉区进路的决策选择,则是咽喉区进路与到发线一体化优化编制:Kroon等[11]指出若每列车可供选择的进路有3条以上时,该问题为NP完全问题,若只有2条进路可供选择时,则问题可以在多项式时间内求解;Zwaneveld等[12]将到发线运用与进路排列的综合优化问题看作一个带权重的节点封装问题,算法的设计基于预处理技术、有效不等式及分支切割法,算法的改进能够为荷兰所有车站高效地排列进路;史峰等[13]建立了到发线运用与一端咽喉区接发车进路排列方案综合优化模型,并提出极大列车进路方案及其k剔除邻域系的概念,在此基础上设计模拟退火算法对问题进行求解;陈彦等[14]研究了旅客列车过站径路优化问题,指出过站径路由列车的接车作业进路、占用的到发线和发车作业进路拼接而成。以旅客列车的接发车作业进路为决策,建立旅客列车过站径路优化的0-1规划模型。设计基于极大列车过站径路方案k剔除邻域系的模拟退火算法求解;Caprara[15]通过构建一个0-1整数规划模型描述列车在车站的进路选择问题,优化目标为最小化期望到发线与实际占用到发线之间的偏差及最小化在接发车进路上可能的冲突,由于目标函数为非线性函数,对其进行线性化处理,其结果优于简单的启发式算法;苗建瑞等[16]以车站资源运用抗干扰性能好为目标,以所有作业都能安排到资源为约束,建立了车站作业计划的混合整数规划模型,设计了基于蚁群的求解算法。当可行解不存在时,算法可给出需要调整到发时刻的列车以及相应的调整量;白紫熙[17]将车站作业计划优化问题看作一个车间调度优化问题,以最小化列车在车站的停站时间为优化目标,以设备能力、车站作业分配、停站时间、进路的冲突疏解为约束建立数学模型,采用拉格朗日和次梯度理论对模型进行简化并设计求解算法,通过实例验证了模型及算法的有效性;乔瑞军[18]以最大化列车选择进路的偏好度、到发线均衡运用等为目标建立进路选择的多目标优化模型,基于目标协调优化思想对济南西站的全天作业列车在图定时刻情况下的到发线与进路排列优化方案进行求解,文中将具有换乘接续关系的列车安排至临靠相同站台的到发线作为约束条件,却未在实例中有所体现;Sels等[19]在现有的列车集及未来的列车集情况下求解每一列车的到发线占用及其接发车进路的排列,基于列车到发时间不允许改变、连通一条到发线仅有一条接发车进路可供选择等假设,建立混合整数规划模型,并对10个车站进行实例分析。通过上述分析,既有文献通常以最小化到发线运用的不均衡性程度、最大化到发线固定使用方案的匹配程度等作为车站作业计划优化编制的目标,而针对考虑列车在车站的同站台换乘接续情况下的车站作业计划优化编制的研究较少且不深入。因此,本文在前人研究的基础上针对基于同站台换乘的高速铁路车站作业计划优化编制问题展开研究。

1模型构建
由于本文的目标在于探索列车在高速铁路车站内进行换乘接续组织的情形,不仅希望尽可能多地组织具有换乘接续关系的列车之间的同站台换乘,而且需要充分确保高速铁路车站的通过能力与车站作业计划的鲁棒性。
高速铁路车站到发线的均衡运用能够使得每条到发线均能够较为紧凑地接发列车,避免出现某些到发线接发列车过于密集,而某些到发线通过能力虚糜的现象[20],即高速铁路车站到发线的均衡运用既能够确保车站作业计划较好的鲁棒性,亦能够保证车站的通过能力。
因此,本文以到发线运用的不均衡程度最小化及同站台换乘能够服务的潜在客流最大化为优化目标,依据车站技术作业原则与模式形成的约束条件,构建多目标0-1整数规划模型解决基于同站台换乘的高速铁路车站作业计划优化编制问题。
1.1构建原则
高速铁路车站作业计划的优化编制包括到发线运用的优化与咽喉区进路选择的优化,由于到发线与咽喉区进路之间相互连通,表现出较强的耦合关系,因此,两者的优化并不是孤立的,应当对两者进行综合协调优化,即考虑到发线与咽喉区的协调配合,实现到发线运用计划与咽喉区进路占用方案的一体化优化编制。
本文将具有换乘接续关系的2列列车分别定义为换乘列车(Transfer Train)和接续列车(Connecting Train)[21],其中换乘列车指中转换乘旅客完成前段旅程乘坐的列车,接续列车指中转换乘旅客完成后段旅程乘坐的列车。若2列列车在换乘接续方向及换乘接续时间2方面均满足换乘接续的条件,则认为这两列列车具备组织换乘接续的条件。从时间及空间两个角度协调分析通过在车站组织同站台换乘而产生的客运产品能够吸引的客流量,将这部分客流称为潜在换乘客流。
模型的建立基于以下假设条件: 1)不考虑咽喉区进路的分段解锁; 2)不考虑列车接入同一到发线经由不同进路走行时间的差异; 3)不考虑立即折返列车中的转线立折列车; 4)不考虑站台能力对旅客同站台换乘的限制。
1.2符号定义

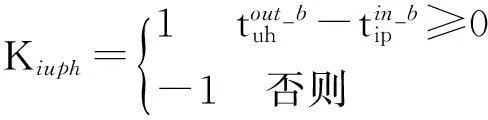
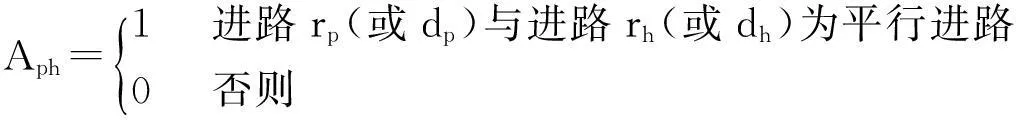
Giu为判断列车ci与列车cu是否为一对立折列车的0-1变量:
xij为列车占用到发线的0-1决策变量:


1.3优化模型
由上述分析确定高速铁路车站作业计划优化编制模型如下:
(1)
(2)
s.t.
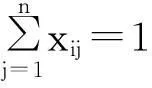
(3)

(4)

(5)
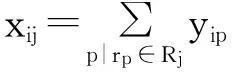
(6)
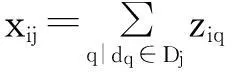
(7)
(8)
∀i,u,p,h, {ci,cu}∈C, rp∈R, dh∈D
(9)
∀i,u,p,h, {ci,cu}∈C, rp∈R, dh∈D
(10)
∀i,u,p,g, {ci,cu}∈C, {rp,rg}∈R
(11)
∀i,u,q,h, {ci,cu}∈C, {dq,dh}∈D
(12)
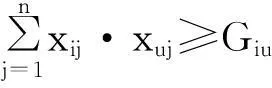
(13)
式(1)表示最小化列车占用到发线不均衡程度,即每条到发线被占用的总时间与到发线被占用的平均时间之差的平方和最小;式(2)表示最大化组织同站台换乘能够服务的潜在换乘客流量;式(3)~(5)分别表示对于任意一列在车站作业的列车,必须并且只能占用一条股道(到发线或正线)、一条接车进路(或出段进路)、一条发车进路(或入段进路);式(6)、式(7)分别表示列车占用的接车进路(或出段进路)、发车进路(或入段进路)与列车占用的到发线(或正线)的连通性;式(8)表示列车占用同一到发线满足最小安全时间间隔约束,即前行列车的出发时刻与后行列车的到达时刻的时间差应当大于等于最小安全时间间隔;式(9)、式(10)表示列车的到发交叉干扰疏解约束,若某一列车占用接车进路(或出段进路)的时间窗与另一列车占用发车进路(或入段进路)的时间窗存在重叠部分(即存在到发时间冲突),则2列车占用的进路应当为平行进路;式(11)表示列车的到达交叉干扰疏解约束;式(12)表示列车的出发交叉干扰疏解约束;式(13)表示若某两列列车为一对立即折返列车(根据动车组运用计划判断),则2列列车依据本线折返的原则占用同一到发线。
2算法设计
2.1编码方案设计
结合本文构建的模型的特点,算法采用符号编码的方式。为了提高算法搜索过程的效率,针对本文构建的模型特别引入广义进路的概念[22]。广义进路是指列车在车站作业占用的接车进路(或出段进路)、到发线及发车进路(或入段进路)组成的一条完整的列车在车站作业进路。
因此,问题的编码方案可以描述为:
1)种群中每个个体的编码长度为所有在车站作业的列车的数量;
2)个体的每个基因位对应在车站作业列车集的每一列车;
3)依据个体每个基因位列车类型的不同,个体每个基因位的值取自其对应的广义进路的编号集合。
2.2适应度函数设计
由于模型为多目标优化问题,采用线性加权法对目标函数进行处理,并构造适应度函数。
针对本文模型的优化目标,其适应度函数的构造过程如下:
1)由于模型的2个优化目标分别为求最小值(Z1)及最大值(Z2),因此将minZ1转变为max(1/Z1);
2)由于线性加权法要求各个优化目标的无量纲化处理,结合遗传算法每一代种群中多个体的特点,对目标函数进行种群层面的归一化处理:
(14)
(15)
其中,px表示种群规模;pi表示个体的序号。
3)确定各优化目标的权重ω1与ω2,则每个个体pi的适应度函数为:
FT(pi)=ω1·obj1(pi)+ω2·obj2(pi)
(16)
其中,加权值ω1对方案中到发线运用的均衡性进行控制,影响车站作业计划的鲁棒性及车站的通过能力;加权值ω2对方案的旅客服务质量进行控制。
2.3遗传算子设计
1)选择算子:采用轮盘赌选择法。根据个体适应度值跟种群的总适应度值之比来确定个体被选择进入下一代的概率。
2)交叉算子:采用单点交叉的方式。在个体串中随机设定一个交叉点,实行交叉时,该点前或后的2个个体的部分结构进行互换,并生成2个新个体。
3)变异算子:采用基本位变异的方式。依据本文的问题特点,为了防止无效解的产生,发生变异的个体基因位的变异范围为其可行的广义进路编号集合。
3实例分析
以武汉站高速场在2014年10月的某一平峰日的作业为基础进行实例分析,验证模型及算法的实用性。武汉站高速场的平面布局图如图1所示。

图1 武汉站高速场平面布局示意图Fig.1 Layout of Wuhan railway station high-speed yard
车站技术作业时间标准是高速铁路车站作业计划的优化编制必要的输入条件,根据模型假设,通过不同进路接入同一股道的2列列车占用接车进路的时间相同(正向接车与反向接车不同)、由同一股道出发经由不同进路离开车场的2列列车占用发车进路的时间相同(正向发车与反向发车不同),因此,确定列车占用接发车进路(或出入段进路)的时间标准如表1所示。
表1列车占用接发车进路的时间标准
Table 1 Time standard of train occupied receiving and dispatching route

连通股道占用接车进路的时间/s占用发车进路的时间/s正向接车反向接车正向发车反向发车126027024025022602702402503220230200210422023020021051801901601706180190160170Ⅶ160-140-Ⅷ160-140-91801901601701018019016017011260-240-12260-240-13220-200-14260-240-15260-240-
列车占用到发线的时间标准是由列车占用接车进路的时间、列车在到发线上的停留时间及列车发车起至列车尾部越过到发线上的出站信号机止的时间共同确定。这里将列车发车起至列车尾部越过到发线上的出站信号机止的时间统一确定为30 s,由列车运行图确定每列列车在到发线上的停留时间,由表1确定了列车占用接发车进路(或出入段进路)的时间标准,因此列车占用到发线的时间能够确定。
采用Matlab软件求解计算。算法的相关参数取值如下:种群规模为800,迭代次数为800,交叉概率pc为0.85,变异概率pm为0.05,优化目标1(最小化列车占用到发线不均衡程度)的权值ω1为0.25,优化目标2(最大化组织同站台换乘能够服务的潜在换乘客流量)的权值ω2为0.25,罚函数(交叉干扰个数)的权值ω3为0.5,列车占用到发线的最小安全间隔时间为5 min。
根据运行结果输出理想解,优化目标1(不均衡度)的值为691 564 173.3/s2,优化目标2(同站台换乘潜在客流量)的值为840/人,罚函数的值为0(即没有交叉干扰)。
3.1优化方案的均衡性分析
模型的优化目标1是最小化列车占用到发线不均衡程度,图2表示模型求解所得的优化方案与既有的武汉站高速场作业计划编制方案的全天各条到发线被占用时间对比。
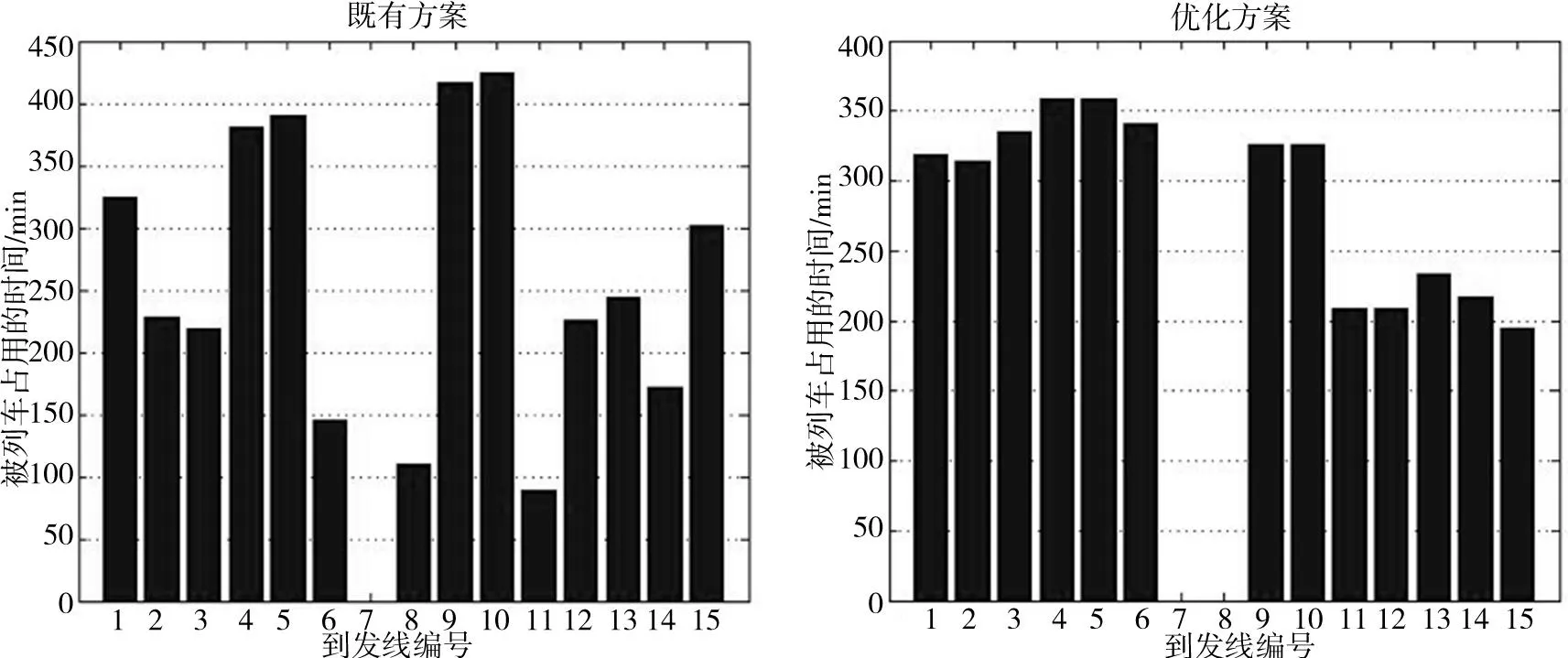
图2 既有方案与优化方案的到发线被占用时间对比Fig.2 Comparison of time arrival-departure tracks be occupied between original plan and optimization scheme
通过计算,既有方案的不均衡度值为827 275 973.3/s2,高于优化方案的不均衡度的值(691 564 173.3/s2)。通过对比可以看出,与优化方案相比,既有方案具有较好的到发线运用均衡性,极大地改善了武汉站高速场到发线运用的不均衡性。
3.2优化方案的同站台换乘接续分析
对2列列车之间是否满足换乘接续条件进行判断,具体的判断原则如下。
1)换乘接续方向判断原则:首先,由换乘车次的始发站至接续车次的终到站若在武汉站中转时,并不造成路径的迂回。例如,北京西至西安北、济南西至上海虹桥若在武汉站中转,则是路径的迂回;其次,换乘车次的终到站与接续车次的终到站不相同,若相同,则没有换乘接续的必要性。
2)换乘接续时间判断原则:依据国外同站台换乘接续的时间经验[23],确定换乘接续时间的原则。首先,接续车次的到达时刻与换乘车次的到达时刻之差不应大于12 min。此原则是为了避免旅客在站台过长时间的滞留,不利于旅客的安全及车站的客流组织工作;其次,接续车次的出发时刻与换乘车次的到达时刻之差不应小于5 min。此原则是为了保证旅客必要的换乘时间。
经过判断,确定具备组织换乘接续的条件的列车对备选集合。模型的优化目标2是最大化组织同站台换乘能够服务的潜在换乘客流量,优化方案能够满足同站台换乘的潜在客流如表2所示。
表2优化方案中同站台换乘接续车次信息
Table 2 Train messages with across-platform transfer in optimization scheme
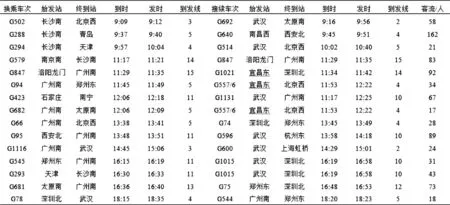
由表2可以看出,优化方案中的同站台换乘接续组织方案具备一定的多样性,从换乘衔接方向的角度,能够满足各类不同OD客流的出行需求,提供了多样化的客运产品供给,丰富了旅客的出行选择;从换乘衔接时间的角度,保证了同站台换乘过程的客运服务质量。
对比既有的武汉站高速场作业计划编制方案,既有方案仅有4对列车能够满足换乘接续的条件,实现站内的同站台换乘,满足潜在客流138人的同站台换乘需求。因此,优化方案能够确保同站台换乘接续的多样性。
综上分析,该高速铁路车站作业计划优化方案在保证到发线运用均衡性的同时,为旅客的出行提供了多样化的选择并保证了旅客的同站台换乘的服务质量。
4结论
1)以到发线运用与咽喉区进路选择一体化优化的原则为导向,并引入车站同站台换乘接续组织因素的基础上,构建基于同站台换乘的高速铁路车站作业计划优化编制模型,以到发线运用的不均衡程度最小化及同站台换乘能够服务的潜在客流最大化为优化目标,并考虑列车在车站技术作业占用设备的唯一性、咽喉区进路与到发线的连通性、列车占用同一到发线的最小安全间隔时间、列车在咽喉区作业的冲突疏解及立折列车作业模式等约束条件,建立多目标0-1整数规划模型。
2)采用遗传算法对模型进行求解,依据模型的特点与遗传算法的形式,从编码方案、适应度函数设计、遗传算子设计3个方面对算法进行设计。
3)以武汉站高速场为背景进行实例分析,从到发线运用的均衡性及同站台换乘接续的多样性2方面对优化方案与既有方案进行对比,验证了模型与算法的可行性与有效性。
参考文献:
[1] Billionnet A. Using integer programming to solve the train-Platforming problem[J]. Transportation Science, 2003,37(2):213-222.
[2] 徐杰, 杜文, 常军乾, 等. 基于遗传算法的区段站到发线运用优化安排[J]. 中国铁道科学, 2003,24(2):109-114.
XU Jie, DU Wen, CHANG Junqian, et al. The genetic based algorithms optimization plan of using the arrival and departure track at railway sectional station[J]. China Railway Science, 2003,24(2):109-114.
[3] 谢楚农, 黎新华. 铁路客运站到发线运用优化研究[J]. 中国铁道科学, 2004(5):132-135.
XIE Chunong, LI Xinhua. Optimization research for utilization of arrival and departure tracks in railroad passenger station[J]. China Railway Science, 2004(5):132-135.
[4] 张苏波, 廖勇, 邹健康, 等. 基于遗传算法的客运站到发线优化安排[J]. 铁道运输与经济, 2007,29(11):24-27.
ZHANG Subo, LIAO Yong, ZOU Jiankang, et al. Optimize the occupation plan of arrival-departure lines in passenger station based on genetic algorithm[J]. Railway Transport and Economy, 2007,29(11):24-27.
[5] 雷定猷, 王栋, 刘明翔. 客运站股道运用优化模型及算法[J]. 交通运输工程学报, 2007,7(5):84-87.
LEI Dingyou, WANG Dong, LIU Mingxiang. Optimization model and algorithm of utilization of arrival and departure tracks in railroad passenger station[J]. Journal of Traffic and Transportation Engineering, 2007,7(5):84-87.
[6] 吕红霞, 何大可, 陈韬. 基于蚁群算法的客运站到发线运用计划编制方法[J]. 西南交通大学学报, 2008(2):153-158.
LÜ Hongxia, HE Dake, CHEN Tao, Method of arrival and departure tracks utilization plan in railroad passenger station based on ant colony algorithm[J]. Journal of Southwest Jiaotong University, 2008(2):153-158.
[7] 张英贵, 雷定猷, 汤波, 等. 铁路客运站股道运用窗时排序模型与算法[J]. 铁道学报, 2011(1):1-7.
ZHANG Yinggui, LEI Dingyou, TANG Bo, et al. Due windows scheduling model and algorithm of track utilization in railway passenger stations[J]. Journal of the China Railway Society, 2011(1):1-7.
[8] 王保山, 侯立新, 刘海东. 客运专线车站到发线运用优化方法[J]. 交通运输系统工程与信息, 2012,12(2):105-110.
WANG Baoshan, HOU Lixin, LIU Haidong, Optimized utilization of arrival and departure tracks in dedicated passenger lines[J]. Journal of Transportation Systems Engineering and Information Technology, 2012,12(2):105-110.
[9] 乔瑞军, 朱晓宁, 张天伟, 等. 客运专线车站到发线运用多目标优化模型[J]. 北京交通大学学报, 2012(3):57-64.
QIAO Ruijun, ZHU Xiaoning, ZHANG Tianwei, et al. Multi-objective optimization model of station arrival and departure tracks utilization for passenger dedicated lines[J]. Journal of Beijing Jiaotong University, 2012(3):57-64.
[10] 吕颖, 马驷, 王琳. 关于高速铁路车站到发线运用优化研究[J]. 铁道运输与经济, 2014(8):26-31.
LÜ Ying, MA Si, WANG Lin. Study on optimization of arrival-departure line using in high-speed railway stations[J]. Railway Transport and Economy, 2014(8):26-31.
[11] Kroon L G, Edwin Romeijn H, Zwaneveld P J. Routing trains through railway stations: complexity issues[J]. European Journal of Operational Research, 1997,98(3):485-498.
[12] Zwaneveld P J, Kroon L G, van Hoesel S P M. Routing trains through a railway station based on a node packing model[J]. European Journal of Operational Research, 2001,128(1):14-33.
[13] 史峰, 陈彦, 秦进, 等. 铁路客运站到发线运用和接发车进路排列方案综合优化[J]. 中国铁道科学, 2009,30(6):108-113.
SHI Feng, CHEN Yan, QIN Jin, et al. Comprehensive optimization of arrival-departure track utilization and inbound-out bound route assignment in railway passenger station[J]. Journal of the China Railway Society, 2009,30(6):108-113.
[14] 陈彦, 史峰, 秦进, 等. 旅客列车过站径路优化模型与算法[J]. 中国铁道科学, 2010,31(2):101-107.
CHEN Yan, SHI Feng, QIN Jin, et al. Optimization model and algorithm for routing passenger trains through a railway station[J]. Journal of the China Railway Society, 2010,31(2):101-107.
[15] Caprara A, Galli L, Toth P. Solution of the train platforming problem[J]. Transportation Science, 2011,45(2):246-257.
[16] 苗建瑞, 于勇, 孟令云, 等. 面向稳定性的高速铁路车站作业计划优化方法[J]. 交通运输系统工程与信息, 2012(3):115-121.
MIAO Jianrui, YU Yong, MENG Lingyun, et al. Stability-oriented optimization of train platforming problem on high speed railway[J]. Journal of Transportation Systems Engineering and Information Technology, 2012(3):115-121.
[17] 白紫熙, 周磊山, 王劲, 等. 基于拉格朗日的高速铁路车站作业优化[J]. 交通运输系统工程与信息, 2014(4):120-125.
BAI Zixi, ZHOU Leishan, WANG Jin, etal. A lagrangian relaxation model for high-speed railway station operation optimization[J]. Journal of Transportation Systems Engineering and Information Technology, 2014(4):120-125.
[18] 乔瑞军. 客运专线车站接发车进路选择与调整问题研究[D]. 北京: 北京交通大学, 2012.
QIAO Ruijun. Research on selection and adjustment of receiving routes and dispatching routes in passenger dedicated line station[D]. Beijing: Beijing Jiaotong University, 2012.
[19] Sels P, Vansteenwegen P, Dewilde T, et al. The train platforming problem: The infrastructure management company perspective[J]. Transportation Research Part B: Methodological, 2014,61(1):55-72.
[20] 朱昌锋. 铁路大型客运站到发线分配耦合优化及时域调整研究[D]. 兰州: 兰州交通大学, 2014.
ZHU Changfeng. Research on coupling optimization of arrival and departure track scheduling for railway large-scale passenger station and its receding horizon adjustment[D]. Lanzhou: Lanzhou Jiaotong University, 2014.
[21] LI Xiaojuan, HAN Baoming, ZHANG Qi. Delay adjustment method at transfer station of high-speed railway[J]. Advances in Mechanical Engineering, 2013(5):1-12.
[22] 王克豹. 客运专线与既有线衔接站到发线运用优化研究[D]. 成都: 西南交通大学, 2011.
WANG Kebao. Optimal operation research on arrival-depart line of cohesion station between passenger dedicated line and exiting line[D]. Chengdu: Southwest Jiaotong University, 2011.
[23] 郭根材, 聂磊, 贺振欢, 等. 基于欧洲列车时刻表的高速铁路列车衔接方案探讨[J]. 北京交通大学学报, 2012(6):21-26.
GUO Gencai, NIE Lei, HE Zhenhuan, et al. Train connection plan for high-speed railway based on European rail timetable[J]. Journal of Beijing Jiaotong University, 2012(6):21-26.
(编辑阳丽霞)
Optimization of High-speed railway station operation plan based onacross-platform transferZHAO Qianrui1,2, ZHANG Qi2
(1. State Key Laboratory of Rail Traffic Control and Safety, Beijing Jiaotong University, Beijing 100044, China;
2. School of Traffic and Transportation,Beijing Jiaotong University, Beijing 100044, China)
Abstract:Based on high-speed railway station operation plan optimization, the across-platform transfer was studied. Aiming at minimizing the unbalanced degree of arrival-departure tracks allocation and maximizing the potentially served transfer passenger flow, a multi-objective 0-1 integer programming model was established based on the principle of coordination optimization between route choices in throat areas and arrival-departure tracks allocation. By using genetic algorithm, the problem was resolved and the efficiency of the algorithm was improved by introducing general route. Case study of high-speed area in Wuhan railway station showed that the model and algorithm is of feasibility and effectiveness.
Key words:high-speed railway; station operation plan; across-platform transfer; genetic algorithm
中图分类号:U292.1
文献标志码:A
文章编号:1672-7029(2016)01-0020-08
通讯作者:张琦(1982-),女,山西太原人,副教授,博士,从事高速铁路运输组织研究;E-mail:qzhang6@bjtu.edu.cn
基金项目:国家自然科学基金资助项目(U1434207);中央高校基本科研业务费专项资金资助项目(2015JBM046);轨道交通控制与安全国家重点实验室自主研究课题(RCS2014ZTY1)
收稿日期:*2015-06-19

