含能流的横磁场中各向同性XY自旋链在有限温度下的热纠缠研究

刘　丹，张金岩

(1.大连民族大学 物理与材料工程学院，辽宁 大连 116605；

2.鞍山市第八中学，辽宁 鞍山 114031)



含能流的横磁场中各向同性XY自旋链在有限温度下的热纠缠研究

刘丹1，张金岩2

(1.大连民族大学 物理与材料工程学院，辽宁 大连 116605；

2.鞍山市第八中学，辽宁 鞍山 114031)

摘要：利用拉氏乘子法构建能流算符，使用多体熵积度量方案计算了三比特系统在温度为零时的纠缠和有限温度下的热纠缠性质；根据拉氏乘子的不同区间分析热纠缠随温度、磁场的变化关系，研究了横磁场中各向同性XY自旋链在能量流影响下的能谱。研究发现：当自旋链中没有能量流时，自旋链的极大纠缠为0.46；而当拉氏乘子大于零时，自旋链中出现能量流动，导致体系的热纠缠增加，热纠缠极大值可达到0.92。自旋链中的能量流动会导致体系的热纠缠增加。当体系处于能流相时，横磁场越大，得到的热纠缠就越大。能流的增加，则会导致体系更容易在较低温度获得较大纠缠。

关键词：热纠缠；自旋链；能流；横磁场

量子纠缠特性研究是量子通信、量子计算等应用的理论基础，对于量子多体系统的描述和理解具有十分重要的作用，已成为目前世界范围内重要的研究课题之一。科学家预测，基于量子多体纠缠理论构建的量子计算机可显著提高经典计算机的计算速度，并可为量子通信提供更加安全的通信方法。目前，在量子纠缠特性的研究上已衍伸发展出了许多具体应用方向，如量子密钥分配[1-2]、量子机密共享[3-4]、量子密集编码[5]、量子安全直接通信[6-8]等。近年来，人们对两体量子态的纠缠[9-12]以及各种类型的多体纠缠态[13-17]已进行了广泛的研究。结果表明，一维量子自旋系统可作为量子纠缠制备、传递的载体，具有十分重要的实用价值。人们在量子信息的范畴内对具有各种相互作用的自旋链模型已做了大量分析和讨论[18-24]，但对处于有限温度和外加磁场下的各种以海森堡相互作用耦合的多比特自旋链的纠缠[25-30]的理论研究还有待深入。一维量子自旋系统反映了许多关于量子本质的有趣现象，近年来成为理论和实验的热点研究内容之一。笔者已对横磁场中各向同性XY自旋链的能谱和温度为零时的基态纠缠[23]进行了分析，并对自旋链中引入能量流时，能流对温度为零时体系基态纠缠的影响进行了讨论[19]。但在实际量子纠缠的制备和输运过程中，温度为零的体系状态过于理想，因此，有必要对体系在有限温度T下系统的热纠缠性质进行进一步的理论研究。

本文在有限温度条件下，使用多体熵积度量方案[31]，研究了含有能流的横磁场中的三比特各向同性XY自旋链的热纠缠问题。分析了含有能流的三比特XY链的有效哈密顿量的能谱，系统在有限温度下的热纠缠，能量流、磁场对热纠缠的影响等体系的纠缠问题。

1含能流的各向同性XY自旋链模型

沿z方向横磁场中的各向同性XY自旋链的哈密顿量有如下形式：

(1)

在这个XY模型中，系统的总能量应守恒。因此，使用文献[24]中的方法构建能流算符。由于局域能流的局域能量满足连续性方程，因此可将宏观能流表示为所有局域能流之和。

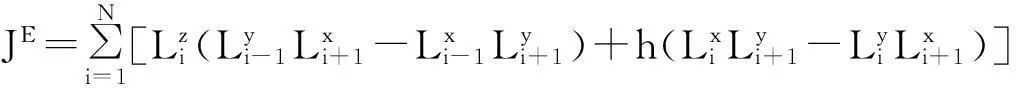
(2)

宏观能流与哈密顿量对易，即[HXY,JE]=0，可用拉氏乘子法将能流算符JE加到系统哈密顿量上构建出如下等效哈密顿量：

HE=HXY-λJE。

(3)

不失一般性，可考虑h≥0，λ≥0。因此，等效哈密顿量HE的任意本征态仍是哈密顿量HXY的定态波函数。HE的基态可看做是温度为零时HXY的携带能流的非平衡稳定态。此时，本征态将携带能流JE，这正是需要的结果。HE只是在数学上构建的用来找到HXY的非平衡态的另一平衡哈密顿量，而系统仍在HXY下演化。以此研究含能流的自旋链的基态纠缠和有限温度下的热纠缠将很有意义。

2含能流的XY自旋链哈密顿量能谱与基态纠缠

以自旋为1/2的三量子比特自旋链作为研究系统，将三比特系统的哈密顿量HE对角化，即可得到如下能谱：

E1=-4-h,

E2=-4+h,

E3=-3h,

E4=3h,

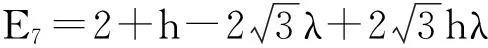
(4)

从三比特各向同性XY自旋链的等效哈密顿量能谱可看出，本征值E1-E4与λ无关，而能级E5-E8都是与λ相关的函数。也即当自旋链处于E5-E8之中的任一能级时，体系中将有能量流动。当λ=0时能级E5，E6及E7，E8是简并的，即E5=E6，E7=E8。当λ≠0，即在自旋链中引入能流后，这种简并现象将消除。

因此，可得与各能级对应的本征波函数如下：

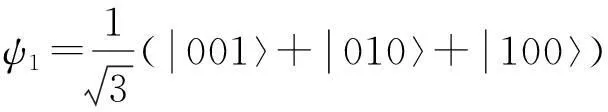
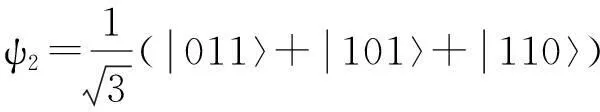
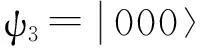
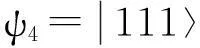
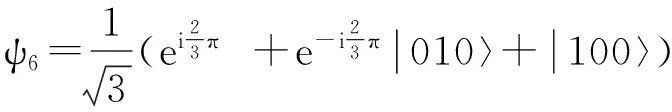
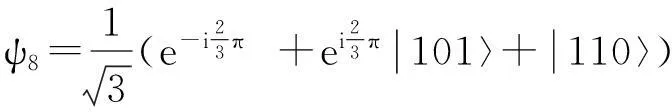
(5)

3含能流各向同性XY自旋链在有限温度下的热纠缠

当系统处于有限温度的热平衡状态时，量子态应表示为所有能量本征态分别按照与能级相关的概率混合而得到的混合态。该热平衡态的密度矩阵可表为

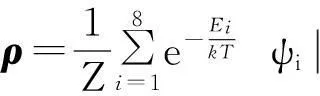
(6)

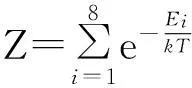
采用多重熵积度量方案[31](multipleentropymeasures,MEMS)来度量纠缠。在MEMS纠缠度量方案中，纯态的纠缠度可表为

…

(7)

MEMS定义混合态的纠缠度为

(8)

式中，Si(j)为纯态的纠缠度Si。因此，式(6)所表示的混合态的纠缠度可写作

(9)

利用式(9)，可以得出体系纠缠度与磁场强度h、拉氏乘子λ和温度T之间的关系。

当λ=0时，随着磁场强度取值的不同，纠缠度S随温度T的变化曲线如图1。由等效哈密顿能谱可知，λ=0时，自旋链中没有能量流动。当T=0时体系处于基态，此时h=2是相变点，这与文献[23]的分析结果一致；当h<2时，热纠缠S随温度T的增加而减小，且随着磁场h的增加，热纠缠S减小得越迅速；当h=0，T=0时，体系的热纠缠有极大值，即Smax≈0.46；当h>2时，S随T的增加而增加，并且随着磁场的增大，热纠缠增大得越迅速，并逐渐趋近于极大值Smax≈0.35。体系最小热纠缠为温度为零的情况。且当T=0时，随着h的增加，最小纠缠将越来越趋近于0。

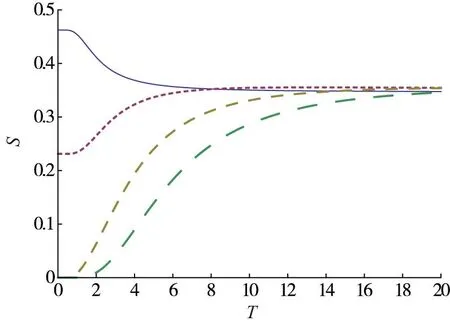
图1　当λ=0，h取不同值时体系

(从左边由上至下分别对应：实线为h=0，点线为h=2，短虚线为h=4，虚线为h=6)

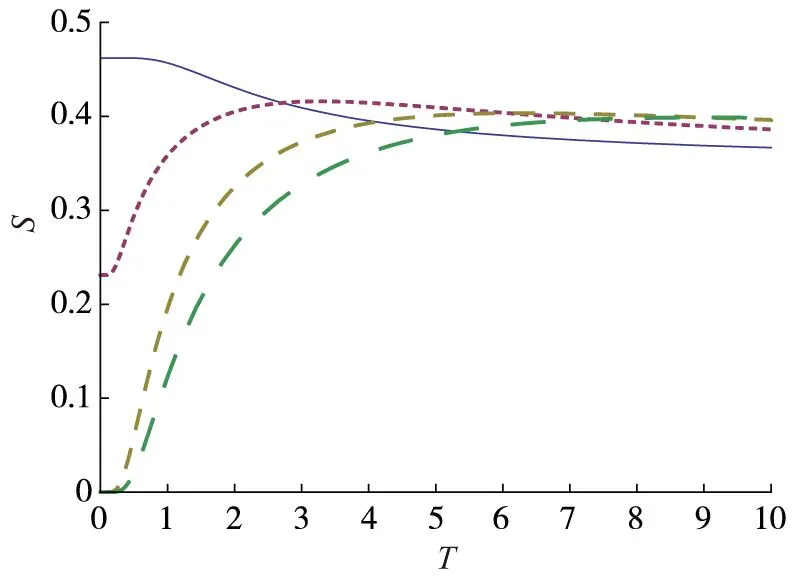
，h取不同值时体系

(从左边由上至下分别对应：实线为h=0，点线为h=2，短虚线为h=4，虚线为h=6)

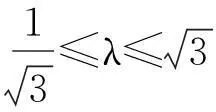
，h取不同值时体系

(从左边由下至上分别对应：实线为h=0，点线为h=0.5，短虚线为h=1，虚线为h=2，长虚线为h=3)

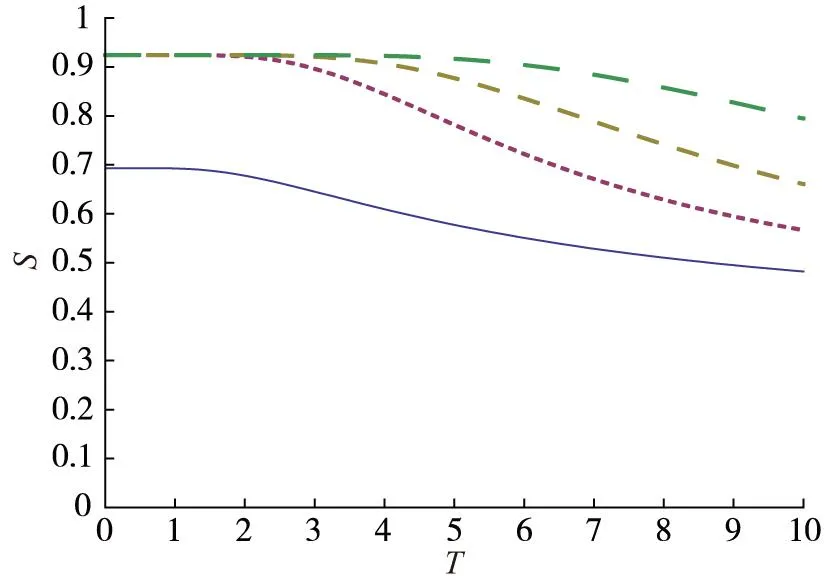
，h取不同值时体系

(从左边由下至上分别对应：实线为h=0，点线为h=0.5，短虚线为h=1，虚线为h=2)

当磁场强度为零时，S在T=0时有最大值Smax≈0.69；当h>0时，热纠缠的最大值为Smax≈0.92。此时热纠缠随温度升高而降低，且磁场强度h越大，热纠缠减小的越慢。

4结语

本文讨论了当自旋链有能量流动时，体系的基态纠缠和有限温度下的热纠缠性质，分析了系统在横磁场和能流影响下，各向同性XY自旋链热纠缠的变化情况。采用文献[24]提出的拉氏乘子法构建了能流算符及等效哈密顿量，并按照表征能量流的拉氏乘子的不同取值区间对热纠缠特性做了详细讨论和理论分析。结果表明，自旋链中的能量流动会导致体系的热纠缠增加。当基态处于非能流相时，体系的极大热纠缠为0.46；而当基态跃变进入能流相之后，极大热纠缠增加为0.92。值得注意的是，这也是三比特XY自旋链可能获得的最大热纠缠。理论分析还发现，基态由非能流相跃变到能流相时，会导致体系的热纠缠增大。且当基态处于能流相时，横磁场越大，体系的热纠缠越大。而能流的增大，将导致体系更容易在较低温度获得较大纠缠。事实上，由于自旋链处于横磁场中，如何进一步考虑磁场流，了解体系的基态纠缠和有限温度下的热纠缠性质，将是我们进一步要研究的内容。

参考文献：

[1]EKERTAK.QuantumcryptographybasedonBell’stheorem[J].PhysRevLett, 1991, 67: 661-663.

[2]LIXH,DENGFG，ZHOUHY.Efficientquantumkeydistributionoveracollectivenoisechannel[J].PhysRevA, 2008, 78: 022321.

[3]LONGGL,LIUXS.Theoreticallyefficienthigh-capacityquantum-key-distributionscheme[J].PhysRevA, 2002, 65: 032302.

[4]LIUD,ZONGZC，MAW.High-capacityquantumsecretsharingwithhyperdensecodingassistedbyhyperentangledphotonPairs[J].IntJTheorPhys, 2013, 52: 2245-2254.

[5]BENNETTCH，WIESNERSJ.Communicationviaone-andtwo-particleoperatorsonEinstein-Podolsky-Rosenstates[J].PhysRevLett, 1992, 69: 2881-2884.

[6]DENGFG,LIXH,LICY,etal.QuantumsecuredirectcommunicationnetworkwithEinstein-Podolsky-Rosenpairs[J].PhysLettA, 2006, 359(5): 359-365.

[7]LONGGL,DENGFG,WANGC,etal.Quantumsecuredirectcommunicationanddeterministicsecurequantumcommunication[J].FrontPhysChina, 2007, 2(3): 251-272.

[8]LIUD,CHENJL，JIANGW.High-capacityquantumsecuredirectcommunicationwithsinglephotonsinbothpolarizationandspatial-modedegreesoffreedom[J].IntJTheorPhys, 2012, 51: 2923-2929.

[9]POURKARIMIM,RAHNAMAM,ROOHOLAMINIH.DecoherenceeffectonquantumcorrelationandentanglementinaTwo-qubitspinchain[J].InternationalJournalofTheoreticalPhysics, 2015, 54(4): 1085-1097.

[10]GONZALEZJC,ROVERSIJA.Decreaseofthedecayrateoftheentanglementofasystemoftwoentangledqubitsbyincreasingthetemperatureofthethermalbath[J].QuantumInformationProcessing, 2015, 14(4): 1377-1385.

[11]SHIJD,XUSM,WENC,etal.Purifyingtwo-qubitentanglementinnonidenticaldecoherencebyemployingweakmeasurements[J].QuantumInformationProcessing, 2015, 14(4): 1387-1397.

[12]GUEVARAI,VIVIESCASC.Averageentanglementdynamicsinopentwo-qubitsystemswithcontinuousmonitoring[J].PhysicalReview, 2014, 90(1): 012338.

[13]JAFARPOURM,ASHRAFPOURIF.Three-qubitprotocoltopurifygeneralizedwernerstates[J].InternationalJournalofTheoreticalPhysics, 2015, 54: 1689-1697

[14]EISLERV,RáCZZ,VANWIJLANGF[J].MagnetizationdistributioninthetransverseIsingchainwithenergyflux.PhysicalReview, 2003,E67: 056129.

[15]ALIZADEHS,SAFAIEER,GOLSHANM.Effectoftemperatureonphoton-photonentanglementinanonlinearnanocavity[J].PhysicaAstatisticalMechanicsandItsApplications. 2015, 428: 133-139.

[16]LILF,CAIRG,LIL.Entanglemententropyinaholographicp-wavesuperconductormodel[J].NuclearPhysicsB, 2015, 894: 15-28.

[17]DUKALSKIM,BLANTERYM.Tripartiteentanglementdynamicsinasystemofstronglydrivenqubits[J].JournalofPhysicsBatomicMolecularandOpticalPhysics, 2012, 45(24): 245504.

[18] ZHAO Y, GONG S S, WANG Y J, et al. Low-energy effective theory and two distinct critical phases in a spin-1/2 frustrated three-leg spin tube [J]. Physical Review, 2012, B86(22): 224406.

[19] LIU D, ZHANG Y, LIU YANG, et al. Entanglement in the ground state of an isotropic three-qubit transverse XY chain with energy current [J]. Chin Phys Lett, 2007, 24(1):8-10.

[20] TAN X D, HUANG S S, JIN B Q. New insights into quantum and classical correlations in XY spin models [J]. European Physical Journal B, 2012, 85(12): 411.

[21] ZENCHUK A I. Unitary invariant discord as a measures of bipartite quantum correlations in an N-qubit quantum system [J]. Quantum Information Processing, 2012, 11(6): 1551-1570.

[22] BRIDGEMAN J C, O'BRIEN A, BARTLETT S D, et al. Multiscale entanglement renormalization ansatz for spin chains with continuously varying criticality [J]. Physical Review, 2015, B91(16): 165129.

[23]刘丹, 宗子超, 邓芸. 横磁场中各向同性XY链的基态纠缠研究[J]. 大连民族学院学报,2013, 15(3): 272-275.

[24] ANTAL T, RACZ Z, RAKOS A, et al. Isotropic transverse XY chain with energy and magnetization currents[J]. Physical Review, 1998, E57(5):5184-5189.

[25] ESKANDARI M R, REZAEE L. Thermal entanglement of two qubits with dipolar ordered initial state coupled to a spin chain in mq nmr system [J]. International Journal of Modern Physics B, 2012, 26(32): 1250184.

[26] HE X, HE J Z, ZHENG J. Thermal entangled quantum heat engine [J]. Physica Astatistical Mechanics and its Applications, 2012, 391(24): 6594-6600.

[27] HUANG X C, SI T Y, YANG Z H. Quantum entanglement investigation on impurity effects in the transverse Ising chain [J]. Physica Bcondensed Matter, 2015, 462: 25-29.

[28] GUO J L, WEI J L, QIN W, et al. Examining quantum correlations in the XY spin chain by local quantum uncertainty [J]. Quantum Information Processing, 2015, 14(4): 1429-1442.

[29] SADIEK G, ALKURTASS B, ALDOSSARY O. Entanglement in a time-dependent coupled XY spin chain in an external magnetic field [J]. Phusical Review, 2010, A82(5): 052337.

[30] ZHANG Y, WANG C, JIN G S. The ground-state entanglement in the spin-XX chain with a magnetization current [J]. Chinese Physics B, 2010, 19(11): 110308.

[31] LIU D, ZHAO X , LONG G L. Extremal entangled four-qubit pure states with respect to multiple entropy measures [J]. Communications in Theoretical Physics, 2008, 49: 329.

[32] ARNESEN M C, BOSE S, VEDRAL V. Natural thermal and magnetic entanglement in the 1D Heisenberg model[J]. Phys Rev Lett 2001, 87: 017901-1-4.

(责任编辑邹永红)

Thermal Entanglement under Finite Temperature of an Isotropic Transverse

XY Spin Chain with Energy Current

LIU Dan1, ZHANG Jin-yan2

(1.School of Physics and Materials Engineering, Dalian Minzu University, Dalian Liaoning 116605, China;

2.The Eighth Middle School of Anshan, Anshan Liaoning 114031, China)

Abstract:The energy current operator was built by Lagrange multiplier method in this paper. The multiple entropy measures were used to calculate both the entanglement under the zero temperature and the thermal entanglement under the finite temperature in the three-qubit system. According to the different interval of the Lagrange multiplier, the changes of thermal entanglement with temperature and magnetic field were analyzed. The energy spectrums were studied under the influence of the energy current in the isotropic transverse XY spin chain. The study found that When the energy current didn’t flow in the spin chain, the maximum value of entanglement in the spin chain was 0.46. When the Lagrange multiplier was greater than zero, the energy current began to flow in the spin chain. Those would make the thermal entanglement increase, and the maximum value could be up to 0.92. The flow of energy would increase the thermal entanglement of the system. When the system was in the energy current phase, the spin chain would have greater thermal entanglement with greater transverse magnetic field. The increase of the energy current would make the system obtain greater entanglement in lower temperature.

Key words:thermal entanglement; spin chain; energy current; transverse magnetic field

中图分类号：O413.1

文献标志码：A

文章编号：2096-1383(2016)01-0056-06

作者简介：刘丹(1979-)，女，湖南益阳人，副教授，博士，主要从事量子光学、量子信息与计算研究。

基金项目：中央高校基本科研业务费专项资金资助项目(DC201502080402)；辽宁省教育厅科学研究一般项目(L2013505)。

收稿日期：2015-06-02；最后修回日期：2015-06-29