基于混沌映射协同差分进化的最优路径规划

刘剑英，杨文艳，刘丹丹

(1.大连职业技术学院 信息工程学院，辽宁 大连 116035；

2. 黑龙江科技大学 电气与控制工程学院，哈尔滨 150022)



基于混沌映射协同差分进化的最优路径规划

刘剑英1，杨文艳1，刘丹丹2

(1.大连职业技术学院 信息工程学院，辽宁 大连 116035；

2. 黑龙江科技大学 电气与控制工程学院，哈尔滨 150022)

摘要：为提高轨迹优化的精度，提出一种基于混沌映射的协同差分进化算法。该模型不依赖数学模型和梯度信息，即可对优化目标进行分组寻优和信息共享，实现快速轨迹优化。在寻优后期的子代构建过程中引入混沌映射，使算法在保持种群多样性的同时，平衡了全局搜索能力和局部搜索能力。通过标准函数对比测试，所提算法在全局寻优能力方面取得明显的改进效果，将其应用于解决轨迹优化的实际问题，可以高效地获得全局最优轨迹，有效地提升差分进化算法的性能。

关键词：差分进化；协同进化；轨迹优化；混沌映射

最优路径规划轨迹优化是运动控制领域中的一个重要分支，在大型矿井中最优路径规划等领域得到广泛的应用[1]。总体目标是使物体运动到指定目标位置，并且不碰到障碍物，与此同时路径最短或耗时最少[2]。自由空间法[3]是其中最经典的方法，该方法将环境空间分为自由空间和障碍物空间两部分，然后采用搜索策略在自由空间中找到一条较优的轨迹，但其计算复杂度受到障碍物数目的影响，不能保证每次获得最优轨迹。随着遗传算法、群体智能计算算法等方法的发展，轨迹优化领域也获得进步[4-5]。

差分进化(Differential Evolution, DE)算法是于1995年为了求解切比雪夫多项式而提出来的一种采用浮点矢量编码在连续空间中进行随机搜索的优化算法[6]。该算法的原理简单，受控参数少，实施随机、并行、直接的全局搜索，易于理解和实现[7-9]。近20年里差分进化算法在自适应控制[10]、遥感图像处理[11-13]等领域得到深入研究。Qu等[14]利用邻域突变特性改进差分进化算法，并将其应用于多峰函数优化。焦李成等[15]提出一种基于差分进化的多目标优化算法，提高了算法的均匀性和宽广性。向万里等[16]提出高效率反向差分进化算法，改进变异搜索方程，获得了较好的收敛精度和速度。在模糊聚类中也可以使用差分进化框架进行有效的初始化[17]。然而由于差分进化算法是根据父代个体间的差分矢量进行变异、交叉和选择操作的，因此，它与其他群体智能算法一样存在早熟收敛现象。此外，差分进化在寻优过程后期，收敛速度会明显减慢。

本文提出一种基于混沌映射的协同差分进化算法，将待优化进行有效分组，然后进行信息共享，提高搜索效率。在寻优后期引入混沌映射机制，提高群体的多样性，从而提高优化结果。最终将其应用于实际最优路径规划问题中，分析其有效性。

1差分进化算法

差分进化算法是通过引入差分变异算子进行迭代的随机算法。首先随机生成初始种群，再利用当前群体中的个体差异构造变异个体，并与第3个随机选择的个体向量进行加权加和，随后将以一定的概率进行杂交生产试验矢量。若试验矢量优于目标矢量，则将较优个体矢量保持到下一代。通过逐步迭代寻找到最优结果。差分进化算法一般包括如下4个基本操作：

步骤1随机初始化

利用均匀随机分布的方法产生初始种群xij：

xij,1=xjmin+rand×(xjmax-xjmin),

i=1,2,…,NP,j=1,2,…,D

(1)

式中，rand为[0,1]之间的随机数，xjmin和xjmax分别为第j个变量的下界和上界，NP为种群规模，D为优化问题的维数。NP越大，种群多样性越强，获得最优解的概率越大。

步骤 2差分变异策略

变异矢量定义为

DG=xr1,G-xr2,G，

(2)

式中，G为进化代数，r1，r2分别为不同的索引号。将差分矢量随机叠加另外一个个体矢量上，实现变异操作如下：

vi,G+1=xr1,G+F×(xr2,G-xr3,G) ，

(3)

式中，r1，r2，r3和i为[1,2,…,NP]中表示3个不同个体，F为变异因子。

步骤 3交叉操作

将群体中的目标矢量个体xi,G与变异矢量vi,G+1进行交叉操作，产生试验矢量个体ui,G+1：

(4)

式中， rand(j)为[0,1]间的随机数；CR为交叉概率因子，取值范围为[0,1]；randn(i)为[1,2,…,D]之间的随机整数。为保证矢量xi,G能够进化，必须使得ui,G+1中至少有一位由vi,G+1贡献。

步骤 4选择策略

通过目标函数进行试验矢量ui,G+1和目标矢量xi,G的选择：

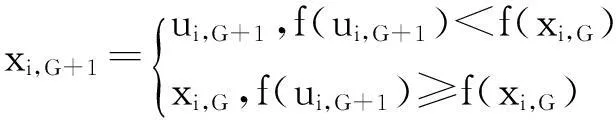
(5)

这里f为目标函数。若ui,G+1的目标函数值小于xi,G的目标函数值，则由ui,G+1替代目标矢量xi,G；反之，则保留xi,G生成新矢量，迭代计算直至符合停止条件。

2基于混沌映射的协同差分进化算法

为了提高差分进化算法的优化能力，构造协同进化框架，将待优化问题进行拆分，然后在每个组内利用混沌映射差分进化算法进行快速寻优，之后进行信息共享。

2.1　协同进化框架

在协同进化(CooperativeCoevolution,CC)框架中，首先对待优化问题进行随机初始化，令最大迭代次数为Tmax，迭代次数变量time=0，种群数目NP，每组内的最大迭代次数T1，整个循环的分组内当前循环次数k=0，进而设定交叉概率因子CR和变异因子F。在整个循环过程中，首先对待优化进行随机分组，拆分成L个小组，分别利用混沌映射差分进化算法(ChaosMappingDifferentialEvolution,CMDE)在小组内进行寻优。之后将各个位置矢量信息进行共享，构建整体矢量，对目标函数进行比较，获得最优个体，循环迭代直至算法收敛停止。协同进化模式可以提高并行计算速度，对大规模模型参数优化具有较好的优势。在利用计算机进行模拟优化的过程中，可以采用图形图像处理单元(GraphicProcessingUnit，GPU)进行硬件上的并行处理分析。通过ComputeUnifiedDeviceArchitecture(CUDA)统一编程平台，利用cudaMalloc和cudaMemcpy命令将GPU计算所需要的参数设定等数据读入到显存中，采用NCVV生成设备端代码。采用Kernel程序为每一个分组建立一个线程块。每个线程代表一个矢量，计算每个矢量的目标函数值，通过每个Block中的共享内存，记录每个矢量的当前位置信息，从而实现组内每个Thread的信息共享和交互，完成变异、交叉和选择的操作，实现子问题的有效快速寻优。当分组寻优之后，满足全局停止条件，将全部结果返回主机内存，获得全局最优位置，提高算法的计算效率。

2.2　 混沌映射矢量变异

混沌运动独有的特征表现为：有界性、遍历性、随机性、分维性、标度性、普适性和统计特征。

定义1混沌定义。 [a,b]上的连续自映射f称为是混沌的，若其满足：

(1)f的周期点无上界；

(2)存在不可数子集S⊂[a,b]，S中无周期点，且满足：

①对任意x,y∈S，有

②对任意x,y∈S，有

③对任意x∈S和f的任意周期点y，有

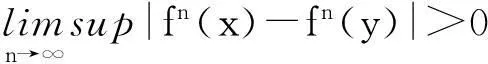
基于混沌映射协同差分进化算法的流程如图1。

基于混沌映射协同差分进化算法首先进行初始化设定，然后对待优化参数随机分组，在每个组内采用混沌映射差分进化算法开始分组寻优，通过信息交互之后，返回上层循环迭代，直至算法收敛。差分进化算法在寻优后期过程中个体差异减弱，整个算法的寻优能力会大幅度的下降，出现“早熟”的现象，所以为了保证轨迹优化过程中搜索的寻优成功概率，就要充分利用混沌映射的遍历性来提高矢量群体的多样性。

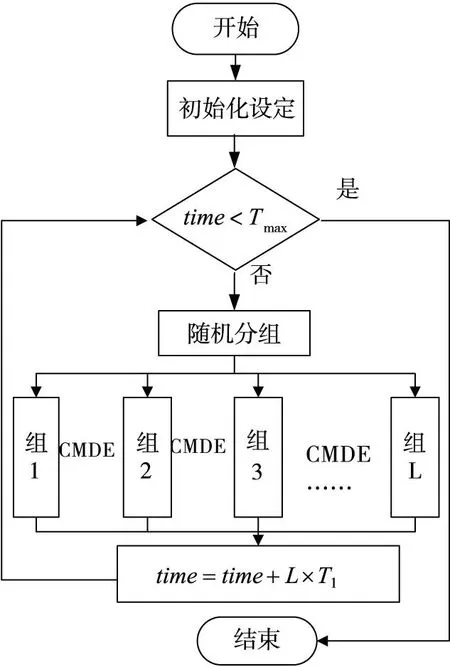
图1　基于混沌映射协同差分进化算法流程图

为进一步确定矢量子代重构标准，对第j个分组内的多样性定义为

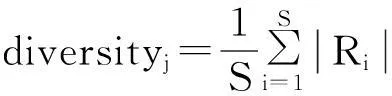
(6)

式中，S为分组内的矢量个数，R为各矢量之间的位置距离。当diversity<ε时，进行子代矢量重构。另一方面采用目标函数变化阈值分析，获得子代重构的判定标准：

f(xn)-f(xn+1)≤ε 。

(7)

当目标函数变化小于ε时，采用混沌重构模式。采用Chebyshev混沌映射，其迭代方程为

xn+1=cos(μacos(xn)),xn∈[-1,1]，

(8)

令μ=4，数据序列处于混沌状态。

当目标函数变化小于ε时，采用混沌重构模式，对矢量中的每一维数据加入混沌变异量，产生NP×D 个混沌随机序列，建立对应矩阵

(9)

然后将混沌随机矩阵赋值于xi,j，产生迁移位置量：

(10)

式中，[xjmin,xjmax]为矢量个体的取值范围，将其加入到原始矢量中，得到新的群体：

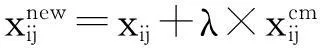
(11)

式中，λ为[0,1]之间的混沌映射编译比例系数，控制矢量混沌迁移的大小。在每个分组内的混沌映射差分进化算法的伪代码如下：

Start

initializethepopulation

evaluatethefitness: = f(x)

While(terminationcondition=false)

Do

Mutation,cross,chooseprocessusing(3), (4)and(5),respectively;

Evaluatethediversityandthechangeoffitnessfunctionusing(6)and(7),respectively;

IF(reconstructcondition=ture)

Calculatechaossequenceandreconstructthevectorsusing(8)-(11);

EndIF

EndDo

End

3基于CMDE-CC的最优路径规划

本研究主要探索运动物体无碰撞且轨迹最短的多目标最优路径规划。在轨迹长度方面，可以通过欧几里得距离而得到长度能量函数——长度能量函数值越小，轨迹长度越短；无碰撞方面，可以通过碰撞罚函数来约束——碰撞罚函数值越小，碰撞的可能性越小，当碰撞罚函数的值小于一定阈值时，表示轨迹无碰撞。因此，多目标最优路径规划的目标函数可以表示为长度能量函数和碰撞罚函数两部分的加权和：

E=wEl+(1-w)Ec，

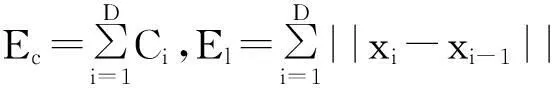
选择起始点和目标点连线上均匀分布的点向量作为初始最优个体，然后再进一步进化寻优。整个流程如图2。

当最优解经过一定代数后没有发生变化或变化不大，而且碰撞罚函数大于一定阈值时，对群体中所有个体进行混沌映射重构，随后进行变异、交叉和选择操作。

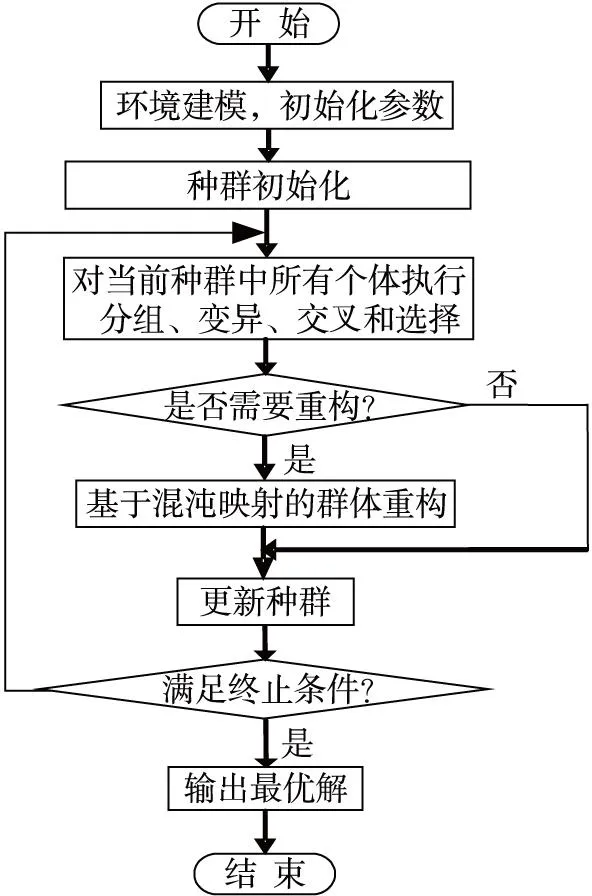
图2　基于CMDE-CC最优路径规划流程图

4仿真分析

为验证所提CMDE-CC算法的有效性，选用4个标准测试函数进行比较不同差分进化算法的有效性。此外，通过最优路径规划模拟实验进行数据对比分析。

4.1　标准函数测试

为了验证所提CMDE-CC算法的有效性，选择4个不同类型的标准测试函数进行分析，这些函数有单峰的、多峰的、连续的、非连续的和不可导的，从而充分验证所提算法的适应性。

标准函数1：Sphere函数

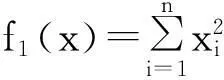
(12)

标准函数2：Ackley‘s函数

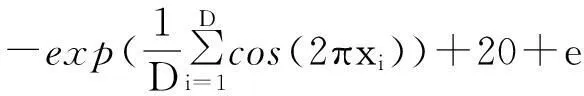
(13)

标准函数3：Griewank’s函数

(14)

标准函数4：复合函数

f1,…,f10:GriewankFunction

[σ1,…,σ10]=[1,…,1]

[λ1,…,λ10]=[5/100,…,5/100]。

(15)

在仿真实验中令维数D分布为100，1 000，其他参数L=10，F=0.5，CR=0.9，NP=100，T1=3 000和Tmax=3 000D。每次实验重复20次，记录其平均值和方差。为了验证所提算法CMDE-CC的有效性，仿真中与经典差分进化算法(DE)和协同差分进化算法(DE-CC)进行比较，仿真结果平均值和方差分别见表1和表2。从数据中可以看出，本文提出的CMDE-CC算法在大部分平均最优值和标准差上精度都有所提高，说明该算法不仅寻优能力更强，而且具有更高的稳定性。

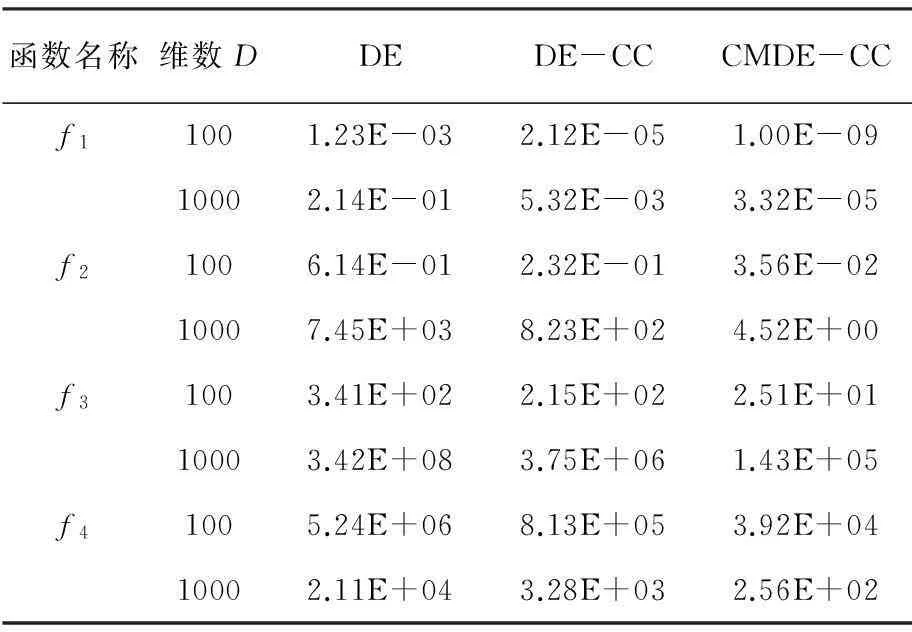
表1　函数优化平均值结果

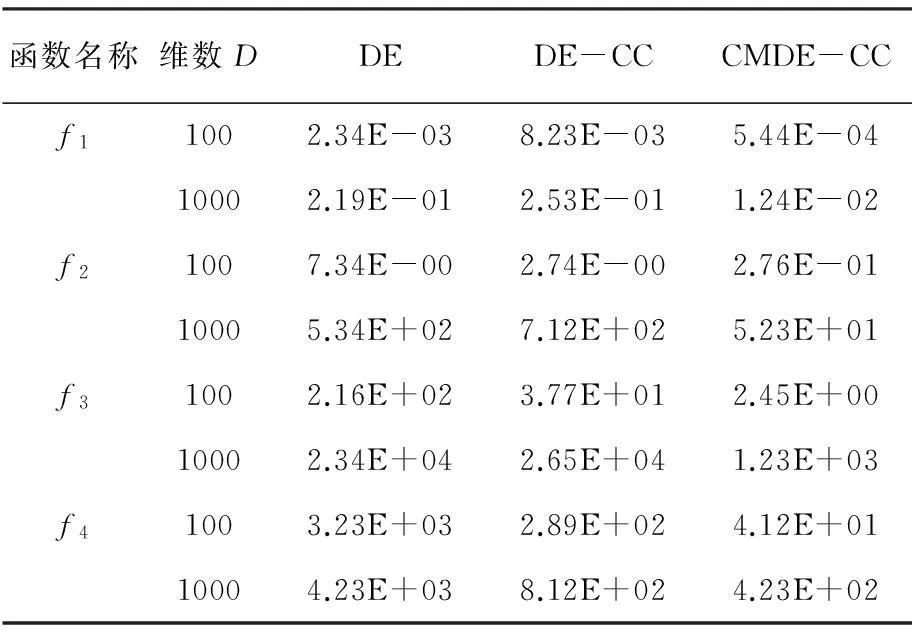
表2　函数优化方差结果

4.2　最优路径规划

采用CMDE-CC算法作为搜索算法，即计算出式(10)的一系列轨迹节点pi,i=1,…,D的位置坐标，采用直角坐标系，故其每个轨迹节点的位置坐标用(xi,yi)来表示，待优化的个体参数矢量可以表示为

xi=[(x1,y1),…,(xi,yi),…,(xD,yD)] 。

(16)

可以看出轨迹节点数越多，得到的轨迹越精确，但是相应所花费的时间也就越长。为了保证精确度，本文中取15个节点，即D=15。为了简化运动物体的模型，本文将运动物体视为质点。CMDE-CC的参数设置为：D=15，NP=100，F=0.5，CR=0.9，n=5，λ=0.3，g=0.001，Tmax=500，T1=100，L=3。目标函数中，w=0.001，起始点坐标p1=[5,5]，目标点坐标pm=[95,95]。路径迭代优化过程中函数变化曲线如图3。

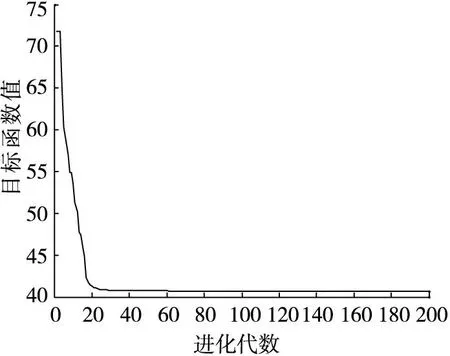
(a)目标函数变化曲线

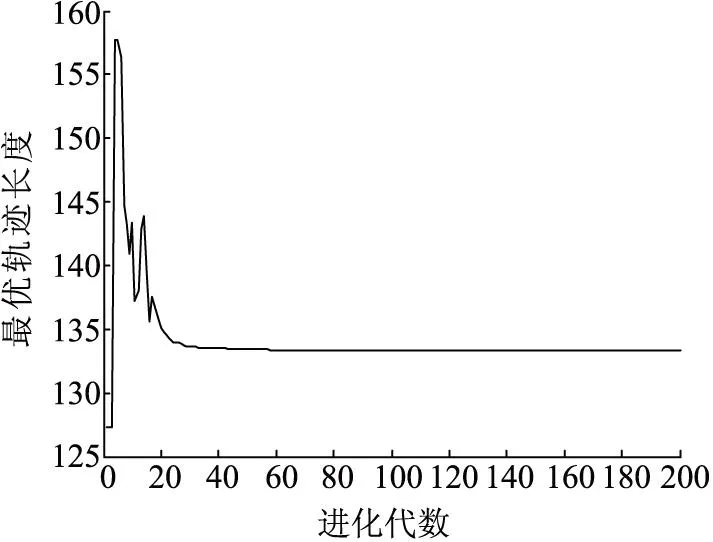
(b)长度能量函数变化曲线

从图3(a)可以看出，CMDE-CC算法在大约40步的时候就已经收敛，而且是全局最优，轨迹长度也是所有可行轨迹中最短的，且没有与障碍物发生碰撞(如图3(b))，即轨迹优化成功。经过CMDE-CC优化得到的最优路径规划结果如图4。

(a)原始最优路径

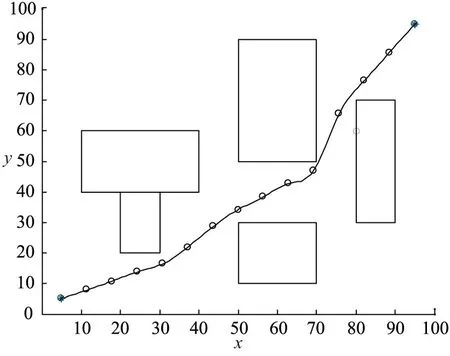
(b)经过差值平滑处理的最优路径

图4(a)为最终得到的最优轨迹，图4(b)将所得最优轨迹经过简单的三次样条插值处理，得到速度与加速度均没有跳变的符合运动学约束的平滑可行轨迹，获得较好的结果。

5结语

本文提出的基于混沌映射协同差分进化算法，不依赖具体问题数学模型，将待优化问题进行随机分解，然后进行分组学习和信息共享，当维数较高时优化效果的改进程度更加明显。此外，在算法的后期引入混沌映射，提高了种群的多样性和算法的优化能力，在最优路径规划的应用中快速准确地寻找到最优路径，充分验证了模型的有效性。

参考文献：

[1] XIA Q L, GUO T, QI Z K. Study of trajectory optimization using terminal-node adaptive-altered spline algorithm [J]. Journal of Systems Engineering and Electronics, 2009, 20(3): 551-557.

[2] KUWATA Y, HOW J P. Cooperative distributed robust trajectory optimization using receding horizon MILP [J]. IEEE Transactions on Control Systems Technology, 2011, 19(2): 423-431.

[3] ALEXOPOULOS C, GRIFFIN P M. Path planning for a mobile robot [J]. IEEE Transactions on Systems Man and Cybernerics, 1992, 22(2): 318-322.

[4] VASILE M, MINISCI E, LOCATELLI M. An inflationary differential evolution algorithm for space trajectory optimization [J]. IEEE Transactions on Evolutionary Computation, 2011, 15(2): 267-281.

[5] FU Y G, DING M Y, ZHOU C P, et al. Route planning for unmanned aerial vehicle (UAV) on the sea using hybrid differential evolution and quantum-behaved particle swarm optimization [J]. IEEE Transactions on Systems Man and Cybernetics: Systems, 2013, 43(6): 1451-1465.

[6] RAINER S, KENNETH P. Differential Evolution-A simple and efficient adaptive scheme for global optimization over continuous spaces [R]. Technical report International Computer Science Institute, Berkeley, California, USA , 1995.

[7] 刘剑英. 基于GPU的并行协同差分进化算法研究[J]. 计算机工程与应用, 2012, 48(7): 48-50.

[8] FAN Q Q, YAN X F. Self-adaptive differential evolution algorithm with discrete mutation control parameters [J]. Expert Systems with Applications, 2015, 42(3): 1551-1572.

[9] 董丽丽, 黄贲, 介军. 云计算中基于差分进化算法的任务调度研究[J]. 计算机工程与应用, 2014, 50(5): 90-95.

[10] GUO H X, LI Y N, LI J L, et al. Differential evolution improved with self-adaptive control parameters based on simulated annealing [J]. Swarm and Evolutionary Computation, 2014, 19: 52-67.

[11] ZHONG Y F, ZHANG S, ZHANG L P. Automatic fuzzy clustering based on adaptive multi-objective differential evolution for remote sensing imagery [J]. IEEE Journal of Selected Topics in Applied Earth Observations and Remote Sensing, 2013, 6(5): 2290-2301.

[12] ZHONG Y F, ZHANG L P. Remote sensing image subpixel mapping based on adaptive differential evolution [J]. IEEE Transactions on Systems Man and Cybernetics, Part B: Cybernetics, 2012, 42(5): 1306-1329.

[13] BAZI Y, ALAJLAN N, MELGANI F, et al. Differential evolution extreme learning machine for the classification of hyperspectral images [J]. IEEE Geoscience and Remote Sensing Letters, 2014, 11(6): 1066-1070.

[14] QU B Y, SUGANTHAN P N, LIANG J J. Differential evolution with neighborhood mutation for multimodal optimization [J]. IEEE Transactions on Evolutionary Computation, 2012, 16(5): 601-614.

[15] 刘若辰, 焦李成, 马亚娟. 一种差分多目标优化算法 [J]. 模式识别与人工智能, 2011, 24(6): 748-755.

[16] 向万里, 马寿峰. 一种高效率收敛的反向差分进化算法 [J]. 小型微型计算机系统, 2014, 35(2): 343-347

[17] POIKOLAINEN I, FERRANTE N, FABIO C. Cluster-Based Population Initialization for differential evolution frameworks [J]. Information Sciences, 2015, 297(10):216-235.

(责任编辑邹永红)

Optimal Trajectory Planning Based on Chaos Mapping

Cooperative Differential Evolution

LIU Jian-ying1, YANG Wen-yan1, LIU Dan-dan2

(1. School of Information Engineering, Dalian Vocational Technology College, Dalian

Liaoning 116023, China;2. College of Electrization and Control Engineering,

Heilongjiang University of Science and Technology, Harbin Heilongjiang 150022, China)

Abstract:In order to improve the precision of trajectory optimization, a cooperative differential evolution algorithm based on chaotic mapping is proposed. The algorithm does not rely on mathematical model and gradient information. It can optimize by group and share information for the optimizing target, and achieve rapid trajectory optimization. We introduce the chaos mapping into the process of children construction in the later period of optimization, which makes the algorithm keep the diversity of the population and balance the ability of global search and local search. By comparing with standard functions, we validate the global optimization ability of the cooperative differential evolution algorithm. Furthermore, the practical application of the algorithm is applied to the trajectory optimization ,which can obtain the global optimal trajectory. The performance of differential evolution algorithm is improved effectively.

Key words:differential evolution; cooperative coevolution; trajectory optimization; chaos mapping

中图分类号：TP391.9

文献标志码：A

文章编号：2096-1383(2016)01-0050-05

作者简介：刘剑英 (1979-), 女，黑龙江黑河人, 副教授，主要从事智能计算、计算机软件研究。

基金项目：国家自然科学基金资助项目 (51374099) 。

收稿日期：2015-06-04；最后修回日期：2015-09-20