人工鱼群算法的改进

唐 莉，张正军，王俐莉

(1.南京理工大学 理学院，江苏 南京 210094；2.海军指挥学院 科研部，江苏 南京 210016)

人工鱼群算法的改进

唐 莉1，张正军1，王俐莉2

(1.南京理工大学 理学院，江苏 南京 210094；2.海军指挥学院 科研部，江苏 南京 210016)

人工鱼群算法(AFSA)是一种新型随机搜索优化算法。通过初步的研究表明，该算法具有许多优良的性质，但也有一些不足之处。针对均匀随机行为和常数拥挤度因子而导致算法运行时间长或陷入局部最优的问题，引入对称正态随机行为，自适应调整该行为参数，减少了由于迂回搜索导致的无用计算，也使人工鱼可在解空间进行更为广泛的搜索，提高了搜索效率。采用了自适应拥挤度因子并提出新的适应度函数，加快了系统满意解的收敛速度，使数值解更加稳定。实验结果表明，与基本人工鱼群算法相比，该方法具有明显的优越性。

随机行为；拥挤度因子；适应度函数；人工鱼群算法；优化

0 引 言

随着动物的进化，根据优胜劣汰的自然法则，它们形成了各式各样的生存方式，这些方式为人类带来了许多灵感和启发。一个动物集群通常定义为一群自治体的集合，自治体是指在自然环境中具备自身活动能力的一个实体。将自治体的概念引入动物优化算法中，通过解决局部问题逐步达到解决最终问题的目的，从而形成人工鱼群算法。该算法是由李晓磊等长时间通过对鱼群生活习性的观察而模仿鱼类生存行动方式提出的，是一种基于动物行为的新型仿生优化随机搜索算法[1]，其归纳总结出符合鱼群行为并适用于鱼群算法的几种典型行为：觅食行为、聚群行为、追尾行为和随机行为。该算法根据“富含营养物质最多的地方一般是水域中鱼生存数目最多的地方”这一特点来模拟各行为，从而实现全局优化，是集群智能思想的一个具体应用，具有并行性、简单性、快速性、较强的鲁棒性和较好的收敛性等特点。但也存在不足之处：

(1)算法在寻优过程中的随机行为，存在迂回搜索的问题，对于求解多极值函数，由于随机行为移动步长太小导致收敛速度慢甚至难以跳出局部最优解。

(2)拥挤度因子δ与人工鱼领域内伙伴的数目nf相结合决定人工鱼群是否执行追尾行为和聚群行为，避免人工鱼过度拥挤而陷入局部极值，但在算法后期，固定数值的拥挤度因子会使得位于极值点附近的人工鱼之间相互排斥，不能进行觅食、聚群和追尾行为，从而无法精确地逼近极值点。

2009年王联国在基本人工鱼群基础上提出全局版人工鱼群[2]；2007年范玉军等对人工鱼移动方式进行改进[3]；刘彦君等采用自适应视野和步长对人工鱼群进行改进[4-6]，采用跳跃行为[7]；黄光球等利用网格划分策略和禁忌搜索算法做了适当改进[8]，并证明了其全局性收敛[9-10]；2008年王联国等基于领域正交交叉算子动态调整视野和步长[11]。

文中引入对称正态行为，自适应调整正态分布方差，并提出新的自适应拥挤度因子对基本人工鱼群算法进行改进。

1 基本人工鱼群算法及参数拥挤度因子δ的性能分析

1.1 相关定义

人工鱼状态定义为X=(x1,x2,…,xn)，其中xi(i=1,2,…,n)为寻优变量；每条人工鱼当前食物浓度表示为Y=f(X)，其中Y为目标函数值，是一个关于xi的n元函数；任意两条人工鱼个体之间的距离表示为di,j=‖Xi-Xj‖；人工鱼所能感应到的视野范围表示为Visual；Step表示人工鱼移动步长；δ表示拥挤度因子；Np表示鱼群个数；trynumber表示尝试次数。

1.2 基本行为

(1)觅食行为。

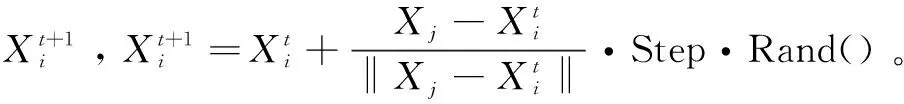
(2)聚群行为。

为了保证鱼群的生存和躲避危害，鱼在游动过程中会自然地聚集成群。在人工鱼群算法中对每条人工鱼做如下规定：一是避免每条人工鱼相互之间过分拥挤；二是人工鱼的移动尽量向临近伙伴的中心靠拢。

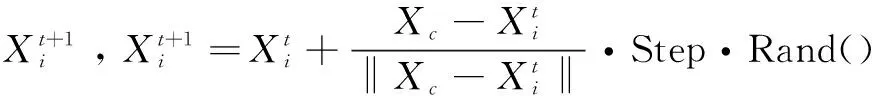
(3)追尾行为。

(4)随机行为。

在需要移动的人工鱼视野范围内随机选择一个状态，然后向该方向移动，该行为事实上是觅食行为的缺省行为：

(1)

1.3 拥挤度因子δ对算法性能的影响

1.3.1 拥挤度因子定义

1.3.2 参数δ的性能分析

δ的引入避免了人工鱼过度拥挤而陷入局部极值，与nf相结合，通过决定人工鱼是否执行追尾行为和聚群行为对寻优产生影响。实验证明[12]，δ越大，人工鱼觅食或者随机行为比较突出，摆脱局部极值能力越强；δ越小，聚群行为和追尾行为在寻优过程中的作用逐渐凸显，有利于提高极值的精确度。而由于每次迭代人工鱼只向鱼群中心位置或鱼群最优位置移动一步，因此影响了算法收敛速度。

2 改进的人工鱼群算法

2.1 引入对称正态随机行为

在基本人工鱼群算法中，觅食行为奠定了算法收敛的基础，聚群行为提供了算法收敛的稳定性，追尾行为增强了算法收敛的快速性和全局性，而随机行为可以逃出局部极值域。然而对于一些多极值函数，特别是达到局部极值与全局最优值的人工鱼所处位置相差甚远时：第一，若该人工鱼X达到局部极值点，而随机行为的步长过小，那么迭代多次仍然可能跳不出局部极值；第二，当人工鱼X迭代至逼近局部极值的位置附近时，若根据该人工鱼的行为评价选择随机行为，那么随机移动步长的过小会使得人工鱼X在局部最优解的附近迂回，反之随机移动步长的过大容易使得人工鱼X跳过全局极值Xbest附近，从而增加收敛时间。

根据上述分析，文中引入对称正态随机行为，采用正态分布随机数调整随机行为中的移动步长step，定义该随机数的方差σ为：

σ=(‖f‖+ε)-1

(2)

动态搜索增强了全局搜索能力，在一定程度上削弱了振荡现象对优化精度的影响并提高了收敛速度。

2.2 自适应拥挤度因子δ

随着δ从大变小，人工鱼逐渐从觅食行为或者随机行为变为聚群行为或追尾行为，在进行全局搜索迭代过程后逼近全局极值点，再逐步进行精确搜素，使结果更加准确。根据上述分析，针对聚群行为和追尾行为中的拥挤度因子δ，定义Xi在当前位置的适应度函数f(Xi)[13-14]为：

(3)

其中，N(Xi)表示当前人工鱼视野范围内感应到的人工鱼个数；di,j表示任意两条人工鱼之间的距离，通常用欧几里德距离；参数αi,j为：

(4)

采用指数式衰减变化策略[10]：δ=δ·T。其中，T=e-β·f(Xi)，β为一固定值，那么T称为衰减因子。随着迭代次数的增加，δ自适应减小，有利于提高搜索解的精度。

2.3 改进的人工鱼群算法步骤

(1)初始参数设置，包括人工鱼群的总数Np、每条人工鱼的初始位置X、移动步长Step、视野范围Visual、尝试次数trynumber以及拥挤度因子δ。

(2)计算每条人工鱼当前的目标函数值Y=f(X)，并在公告板中记录所有函数值中全局最优的人工鱼状态X。

(3)对每条人工鱼评价即到达全局最优的人工鱼保持不动，未到达的进行移动并选择所要执行的行为，包括觅食行为、聚群行为、追尾行为和对称正态随机行为。

(4)将人工鱼移动后与公告板中的值进行比较，更新每条人工鱼目前所处的位置信息。

(5)更新全局最优人工鱼的状态。

(6)根据循环条件，一般为判断连续所得最优目标函数值的均方差小于允许的误差，或判断聚在某个区域内的人工鱼数目达到某个值(某个比例)，或判断连续多次所获取的值均不超过已寻找的极值的次数，或设置最大迭代次数等，则输出结果，否则返回步骤(2)。

3 仿真实现

在Matlab7.0环境下，选取两个经典测试函数进行实验。

实例1：函数。

(5)

该函数在(0,0)处存在唯一极大值1，原点附近散布着一些局部极值。

参数选取：人工鱼总数Np=20，迭代次数IT=50，步长Step=0.7，尝试次数trynumber=5，视野范围Visual=10。下面分别在图1和图2中给出基本人工鱼群算法(AFSA)和改进人工鱼群算法(IAFSA)公告板中最优值的收敛曲线。其中，b_vaule曲线代表公告板最优值，afs_value表示每经过一次迭代后所有人工鱼中的最优值。并在表1中记录了两种算法的执行时间、最优人工鱼极值点(best_x，best_y)及公告板最优值b_value。

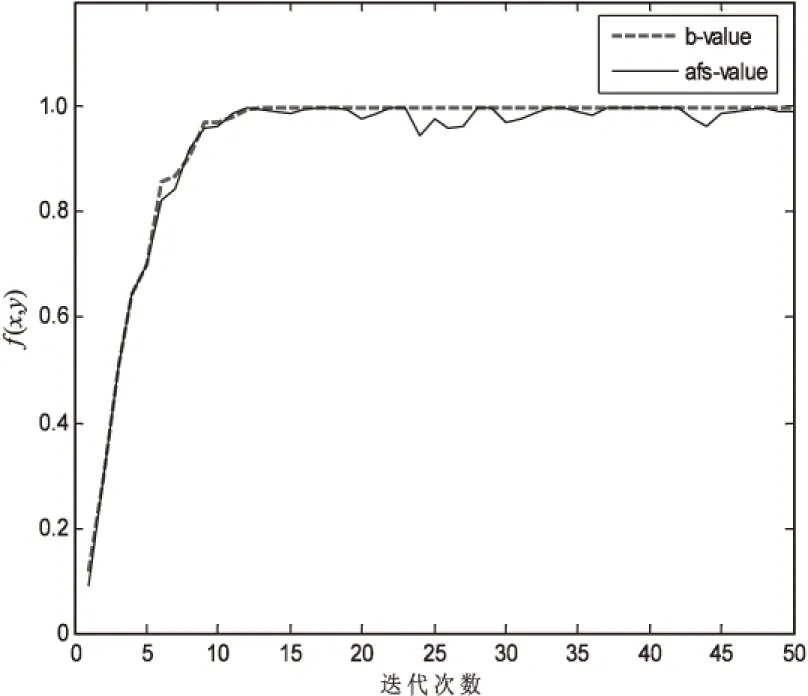
图1 AFSA实例1的收敛曲线

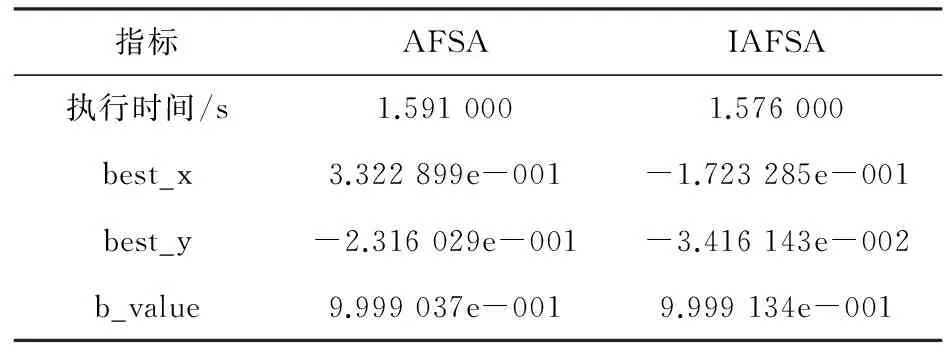
指标AFSAIAFSA执行时间/s1.5910001.576000best_x3.322899e-001-1.723285e-001best_y-2.316029e-001-3.416143e-002b_value9.999037e-0019.999134e-001

从表1可以看出，在时间上IAFSA算法比AFSA加快1%，距极大值点(0，0)近0.229 356 9，且更加收敛于极大值1。

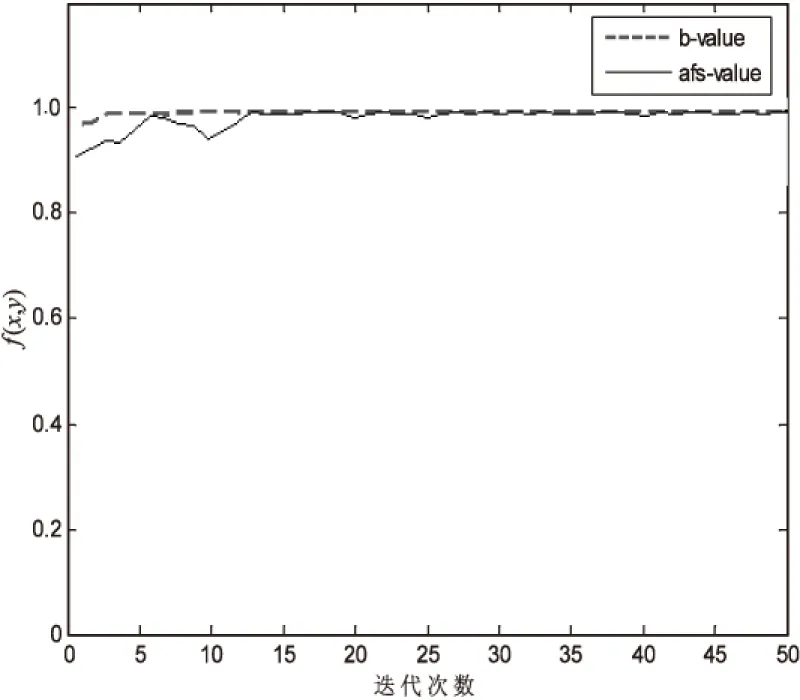
图2 IAFSA实例1的收敛曲线

实例2：函数(Needle-in-a-haystack)。

该函数为典型的多极值问题，其中(0,0)点为全局极值点，且全局最优值为3 600，(-5.12，5.12)、(-5.12，-5.12)，(5.12，-5.12)、(5.12，5.12)为函数的四个局部极值点，且局部极值为2 748.782 3。

参数选择：人工鱼总数Np=60，迭代次数IT=200，步长Step=0.2，尝试次数trynumber=1，视野范围Visual=2。

图3、图4分别为AFSA和IAFSA的收敛曲线，表2为对应的执行时间、最优人工鱼位置(best_x，best_y)及公告板最优值b_value。

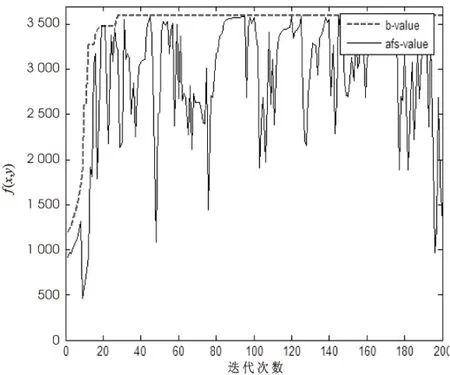
图3 AFSA实例2的收敛曲线

从表2可见，IAFSA算法比AFSA时间加快了1%，距极大值点(0,0)近0.008 938 7，且同样更收敛于极大值1。

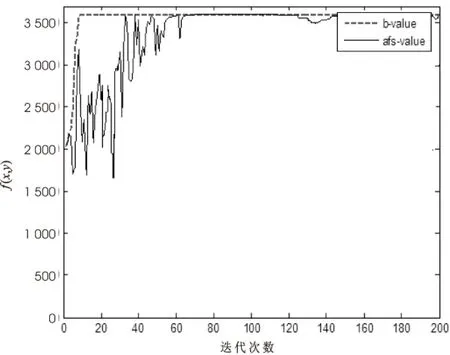
图4 IAFSA实例2的收敛曲线

指标AFSAIAFSA执行时间/s33.29000032.963000best_x-3.070736e-0022.420133e-002best_y2.586932e-0021.971042e-002b_value3.597964e+0033.599593e+003

综上所述，基本人工鱼群算法获取的是近似最优解，改进的人工鱼群算法不仅缩短了算法运行时间，而且具有更好的稳定性和更高的优化精度。

4 结束语

人工鱼群算法是一种新型随机搜索优化算法，具有许多优良的性质。文中引入对称正态随机行为，对基本人工鱼群算法中的随机行为进行改进，减少了迂回搜索的无用计算，同时采用自适应拥挤度因子并提出新的适应度函数，加快了系统满意解的确定。结果表明，与基本人工鱼群算法相比，该方法有效可行。

[1] 李晓磊,邵之江,钱积新.一种基于动物自治体的寻优模式：鱼群算法[J].系统工程理论与实践,2002,22(11):32-38.

[2] 王联国,洪 毅,施秋红.全局版人工鱼群算法[J].系统仿真学报,2009,21(23):7483-7486.

[3] 范玉军,王冬冬,孙明明.改进的人工鱼群算法[J].重庆师范大学学报:自然科学版,2007,24(3):23-26.

[4] 刘彦君,江铭炎.自适应视野和步长的改进人工鱼群算法[J].计算机工程与应用,2009,45(25):35-37.

[5]JiangMingyan,MastorakisNE,YuanDongfeng.Multi-thresh-oldimagesegmentationwithimprovedartificialfishswarmalgorithm[C]//ProcofEuropeancomputingconference.AthensGreece:Springer-Verlag,2007.

[6] Jiang Mingyan,Yuan Dongfeng.Wavelet threshold optimization with artificial fish swarm algorithm[C]//Proceedings of 2005 international conference on neural networks.Piscataway,USA:IEEE Press,2005:569-572.

[7] Jiang Mingyan, Yuan Dongfeng, Francisco R,et al.Spread spectrum code estimation by artificial fish swarm algorithm[C]//Proc of IEEE international symposium on intelligent signal processing.Madrid,Spain:IEEE,2007.

[8] 黄光球,王西邓,刘 冠.基于网格划分策略的改进人工鱼群算法[J].微电子学与计算机,2007,24(7):83-86.

[9] 黄光球,刘嘉飞,姚玉霞.人工鱼群算法的全局收敛性证明[J].计算机工程,2012,38(2):204-206.

[10] Iisufescu M.Finite Markov processes and their application[M].Chichester,UK:Wiley Press,1980.

[11] 王联国,施秋红.人工鱼群算法的参数分析[J].计算机工程,2010,36(24):169-171.

[12] 徐晓华,陈 崚.一种自适应的蚂蚁聚类算法[J].软件学报,2006,17(9):1884-1889.

[13] 朱 峰,陈 莉.一种改进的蚁群聚类算法[J].计算机工程与应用,2010,46(6):133-135.

[14] 陈广洲,汪家权,李传军,等.一种改进的人工鱼群算法及其应用[J].系统工程,2009,27(12):105-110.

Improvement of Artificial Fish Swarm Algorithm

TANG Li1,ZHANG Zheng-jun1,WANG Li-li2

(1.School of Science,Nanjing University of Science and Technology,Nanjing 210094,China; 2.Research and Development Section,Nanjing Naval Command Academy,Nanjing 210016,China)

Artificial Fish Swarm Algorithm (AFSA) is a new random search optimization algorithm.The preliminary study shows that it has many promising features,but also some disadvantages.Aiming at the problem of AFSA,such as long running time or being in local optimal,caused by uniformly random behavior and constant of congestion factor.Based on symmetric normality random behavior,self-adaption adjusts the parameter of this behavior,and a large number of unused circuitous searches are reduced,and a more complete search within solution space is obtained for artificial fishes so that a high search efficiency is arrived at.The self-adaption congestion factor is adopted and a new fitness function is porposed,increasing the convergence rate of satisfactory solution domain,making the result more stable.Results of experiments show that there is an obvious advantage for this improved method compared with the basic artificial fish-swarm algorithm.

random behavior;congestion factor;fitness function；artificial fish swarm algorithm;optimization

2016-01-27

2016-05-05

时间：2016-10-24

全国统计科学研究计划重点项目(2013LZ45)

唐 莉(1993-)，女，硕士研究生，研究方向为数据挖掘与分析；张正军，博士，副教授，研究方向为数据挖掘与分析。

http://www.cnki.net/kcms/detail/61.1450.TP.20161024.1114.060.html

TP301.6

A

1673-629X(2016)11-0037-04

10.3969/j.issn.1673-629X.2016.11.008