基于梁段有限元法的悬索桥板桁结合型加劲梁剪力滞分析

李 磊，颜智法，车世杰

(1.浙江省交通规划设计研究院，杭州 310006；2.中交公路规划设计院有限公司，北京 100088；3.岱山县秀山投资开发有限公司，舟山 316200)

基于梁段有限元法的悬索桥板桁结合型加劲梁剪力滞分析

李 磊1，颜智法2，车世杰3

(1.浙江省交通规划设计研究院，杭州 310006；2.中交公路规划设计院有限公司，北京 100088；3.岱山县秀山投资开发有限公司，舟山 316200)

悬索桥板桁结合型加劲梁桥面系与主桁共同受力，桥面系剪应力沿截面横向分布不均匀，使其弯曲正应力的横向分布呈曲线性状，此即剪力滞效应。相比采用实体或板壳单元进行板结合桁梁剪力滞分析建模复杂、效率低下等问题，利用最小势能原理，采用梁段有限元法的思路，以桁架梁连续化为基础，提出了一种计入剪切变形、剪力滞翘曲影响的悬索桥板桁结合桥面系加劲梁的平面薄壁梁单元，并在求解过程中考虑大变形的影响，推导了加劲梁单元刚度矩阵和几何刚度矩阵，并据此编写了计算程序。利用本程序对简支板桁结合型加劲梁和拟修建的三跨连续悬索桥的控制截面桥面板应力、主梁位移、截面有效宽度和剪力滞力矩进行了计算，并与采用板壳有限元法的计算结果进行了比较。结果表明，计算结果与板壳有限元法结果吻合较好。所建立的考虑剪切变形、剪力滞效应和大变形影响的梁段有限元法便于程序化，适用性和可扩展性强，便于工程计算使用。

梁段有限元法；板桁结合型加劲梁；平面薄壁梁单元；剪力滞；大变形

0 引 言

板桁结合型加劲梁是近几年发展起来的一种新的悬索桥加劲梁结构形式，与传统的分离式桥面系相比，其将桥面系与主桁结合起来，两者相互约束，共同受力。板桁结合加劲梁的采用提高了加劲梁的抗弯刚度和抗扭刚度，减轻了结构自重。目前已通车的板桁结合型加劲梁悬索桥有塔科玛新桥[1]、香港青马大桥；在建的有湖南洞庭湖二桥、贵州清水河大桥等。分离式桥面系、板桁结合桥面系如图1所示。

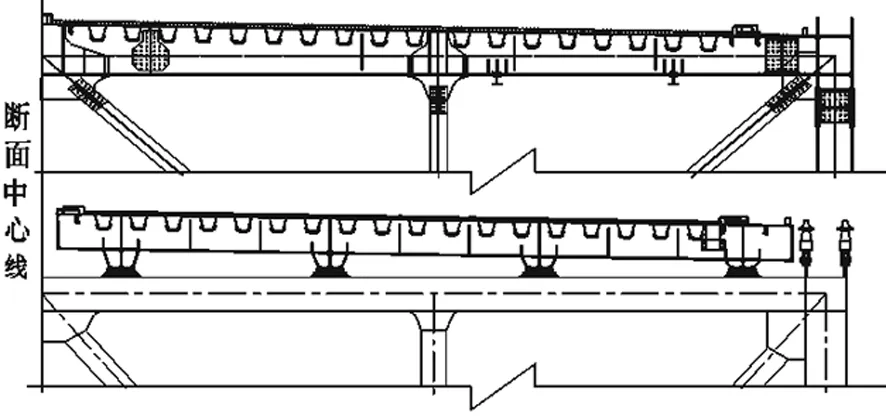
图1 加劲梁型式(上:板桁结合式；下:分离式)

1 问题提出及解决思路

板桁结合加劲梁由于桥面系与主桁共同受力，其计算较为复杂。若采用实体或板壳单元进行板结合桁梁剪力滞分析，则存在建模复杂、效率低下等问题。为提高计算效率，文献[2]中以桁梁连续化为基础，提出了基于离散吊索力、弯矩影响区间的剪力滞求解方法，其对于纵向位移函数中仅考虑一个纵向位移差的情况适用性很好，但当截面中含有多个纵梁需要通过多个纵向位移差函数来更好地考虑截面剪力滞效应时，变分法解析推导将变得极为复杂，且不一定能够得到各广义位移的闭合解。本文仍以桁梁连续化[3-4]为基础，以单层板桁结合桥面系加劲梁为例，采用梁段有限元法的思路对此进行求解，提出一种计入剪切变形、剪力滞翘曲影响的板桁结合桥面系加劲梁的平面薄壁梁单元，并在求解过程中考虑大变形的影响，该方法能够较好地解决文献中提到的问题，且可以从单层板桁结合桥面系拓展到双层板桁结合桥面系、多主桁的板桁结合桥面系桁梁中进行使用。根据上述的描述，对于本文板桁结合型加劲梁剪力滞求解的关键是进行弹性刚度矩阵及几何刚度矩阵的推导，现简要介绍如下。

2 弹性刚度矩阵推导

用变分法的最小势能原理来进行剪力滞问题的分析，具有物理概念清楚、公式简单、计算方便且能满足工程要求精度的优点，在工程中较为常用。本文选取三个独立的广义位移W(x),Q(x),U(x)以考虑腹板剪切变形的影响。

2.1 截面位移参数

采用截面形心处的广义位移作为截面的参考，广义位移向量表示如下：

{u}={uc,wc,θz,U}

(1)

式中：uc、wc分别为截面形心处的平面位移；θz为截面绕z轴的转角；U为剪力滞翘曲位移差。

对于平面梁问题，板桁结合桥面系薄壁梁内任一点的位移可以用截面形心处的广义位移参数表示为：

(2)

式中：ω(z)为与U(x)相应的广义坐标即剪滞翘曲位移函数。

2.2 体系的应变能

∏

+ωξ2(z)(U′)2+2htθ′ωξ(z)U′]+2Gtt(ωξ′)2U2dzdx

(3)

5 算 例

5.1 板桁结合桥面系简支桁梁

采用文献[6]76页中的桁梁参数，建立一桁架腹杆系简支梁结构，对每个节点施加F=2000kN，计算简图如图2；跨中位置应力计算结果如图3，位移计算结果如图4。

图2 板桁结合桥面系简支梁计算简图(单位：m&kN)

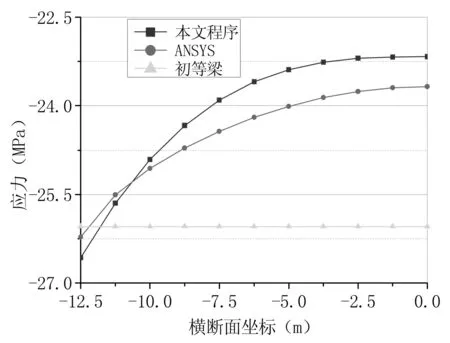
图3 跨中截面应力结果(x=61m断面)

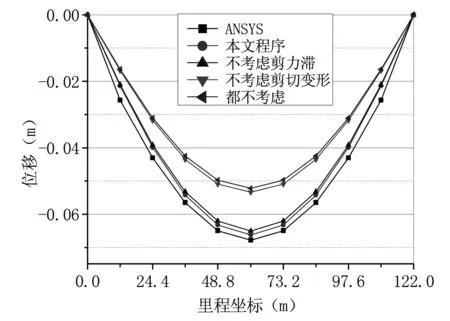
图4 位移计算结果

从图3可知，本文程序计算跨中截面的最大应力为-23.17MPa，最小应力为-26.58MPa；ANSYS计算跨中截面最大应力为-23.67 MPa，最小应力为-26.23 MPa，误差为2.6%。从图4可知，本文程序与ANSYS跨中位移差值仅为2.4%，由此说明本文程序对于板桁结合桥面系桁梁的计算具有较高的精度。另外对于本算例，由剪力滞引起的位移增量为2%，而由剪切变形引起的位移增量达24%。

通过以上算例，对于高跨比较大的板桁结合桥面系桁梁或者实腹板薄壁箱梁，剪力滞引起的位移增量一般较小可以忽略不计，但必须考虑剪切变形的影响，否则位移的计算结果有较大误差，但对应力没有影响。另外采用纵向位移函数为三次抛物线曲线形式得到的应力结果在最大值与ANSYS计算结果较为接近，在截面中心处的应力结果与ANSYS有一定的偏差。

5.2 板桁结合桥面系加劲梁悬索桥

同样以文献[6]中的桁架悬索桥为算例：

采用板桁结合桥面系结构型式的铁路悬索桥加劲梁，加劲梁为97.6m+660m+97.6m三跨连续梁，主缆跨径布置为132m+660m+132m，桥梁总体布置及加劲梁标准断面如图5所示。

图5 某铁路悬索桥总体布置图(单位：m)

以索塔处上弦杆最不利受力工况进行加载分析，同样采用ANSYS进行全桥板壳元有限元分析，如图6所示。计算得到桥塔断面处的应力见图7，全桥有效宽度比分布如图8所示。

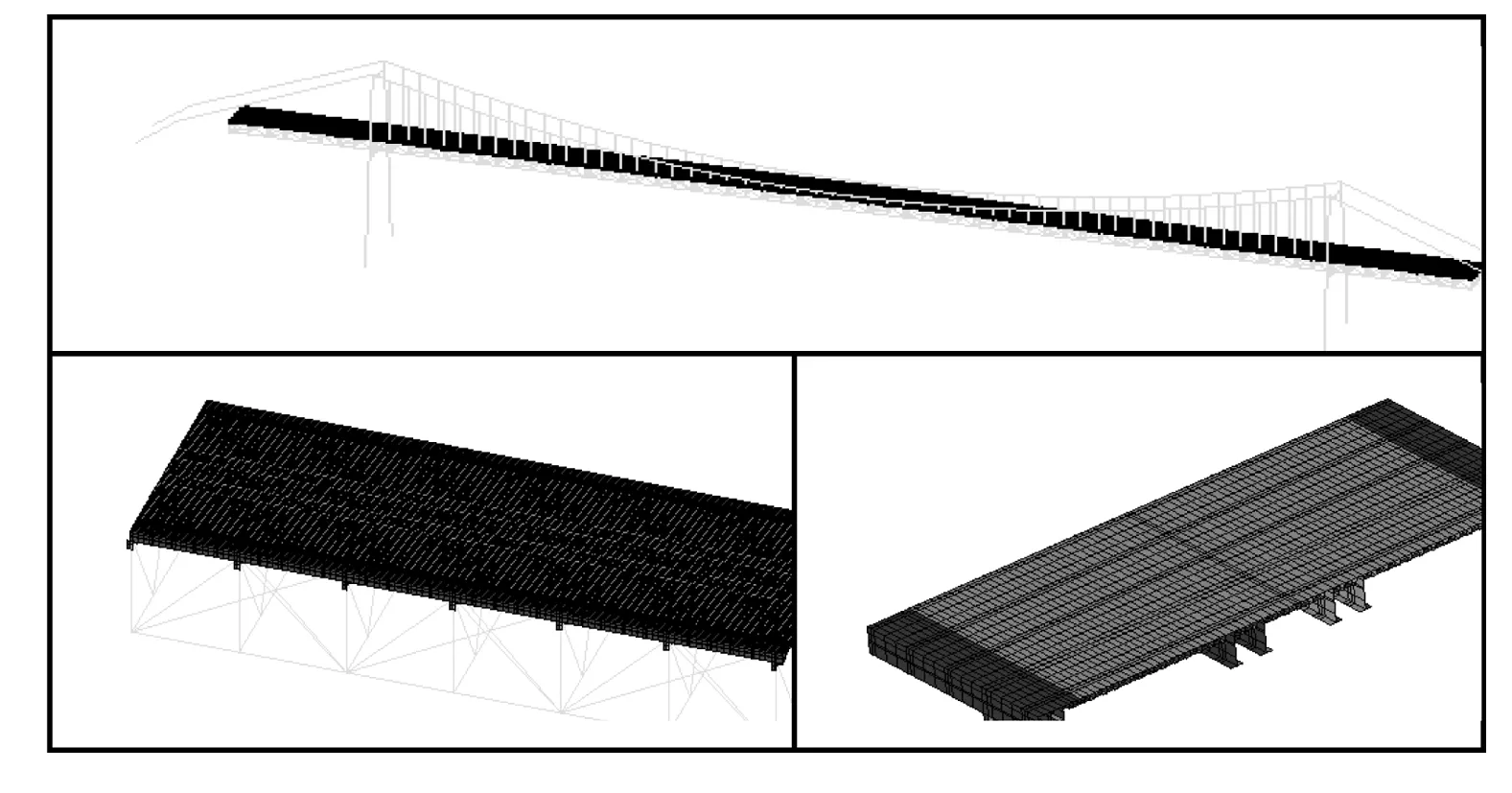
图6 有限元计算模型

从图7可知：本程序计算的应力结果与有限元计算结果规律大致相同。

对于桥塔处截面(里程-330m)：有限元计算钢桥面盖板应力在与弦杆接触处达到最大116.0MPa，在截面中心处最小值69.6MPa，有效宽度比0.721；本文程序计算得到了应力最大值为114.5MPa，最小值85.6MPa，有效宽度比为0.79，有效宽度比与有限元计算结果误差为9.7%，主要是由于本文应力结果在截面中心部较有限元结果大引起，该问题主要是由于桥塔附近截面的纵向位移函数的假定与真实情况有一定差异导致。

对于跨中处截面(里程-146.4m)：有限元计算结果最大值为-50.1 MPa，最小值为-52.8 MPa，有效宽度比0.97；本文程序计算该截面最大应力为-51.7 MPa，最小应力-52.7 MPa，有效宽度比为0.97，该截面有限元计算与本文程序吻合较好。

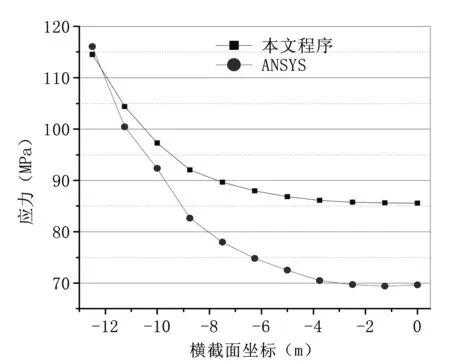
图7 桥塔处应力分布

图8 全桥有效宽度比分布

在初等梁理论中，与弯曲转角相对应的内力为弯矩，与轴向位移相对应的内力为轴力，张元海在文献[7]中提出了与剪力滞位移相对应的内力为剪力滞力矩。本文将不同位置主梁的剪力滞力矩计算汇总于图9。剪力滞矩与弯矩的分布规律相同，且弯矩与剪力滞力矩的比值约为20左右。

图9 剪力滞矩计算结果

6 结 语

(1)梁段有限元法适用性较强，能够较为方便的计算得到截面任意点处的应力、截面的剪力滞系数及有效分布宽度，且能够考虑大变形的影响。

(2)本文所有剪力滞计算模型均是以三次抛物线纵向位移函数为基础，通过算例计算可知，该曲线对于高跨比较大的板桁结合桥面系桁梁的适用性较好；该曲线对于板桁结合桥面系截面中心的应力计算有一定的误差，但应力最大值能够较好地吻合。因此，下一阶段需要对更合理的纵向位移函数进行研究。

(3)本文提出的梁段有限元的方法进行板桁结合加劲梁悬索桥剪力滞分析，方便快捷，易于程序化，推广性较强，具有一定的工程参考。

[1]KP Serzan，T Spoth.Advancements of New Narrows Suspension Bridge Design in Tacoma,Washington[J].Transportation Research Record Journal of the Transportation Research Board,2008,(2050):59-66.

[2]沈锐利，颜智法，唐茂林，等.悬索桥板桁结合型加劲梁剪力滞计算的简化方法[J].桥梁建设，2015，45(3)：82-87.[3]彭旺虎.合成桥面桁梁悬索桥静动力分析理论研究[D].长沙:湖南大学,2013.

[4]李国豪.桥梁结构稳定与振动[M].北京:中国铁道出版社,2002.

[5]项海帆.高等桥梁结构理论(第二版)[M].北京:人民交通出版社,2013.

[6]颜智法.悬索桥板桁结合桥面系力学特性及剪力滞计算方法研究[D].成都:西南交通大学,2014.

[7]张元海.箱形梁桥剪滞效应和温度效应理论研究及其应用[D].成都:西南交通大学,2008.

Finite Segment Method for the Shear Lag Effect in Integral Orthotropic Truss Girders of Suspension Bridge

LI Lei1, YAN Zhi-fa2,CHE Shi-jie3

(1. Zhejiang Provincial Institute of Communications Planning, Design & Research, Hangzhou 310006，China; 2.CCCC Highway Consultants Co., Ltd., Beijing 100088，China; 3. Daishan Investment Development Limited, Zhoushan 316200，China)

The integral orthotropic truss girder is a type of girder which combines deck and truss to an integrity and make them work together. Since the shear stress of deck is unevenly distributed along the horizontal direction of section, the transverse distribution of bending normal stress is in the shape of curve. This is known as the shearing lag effect. Based on the minimum potential energy principle and finite segment method and assuming that the truss girder is continuous, a type of plane thin-walled beam element for integral orthotropic truss girder of suspension bridge which has already considered the influence of shear deformation and shear lag is presented. Besides, the large deformation situation has been taken into account during the solutions, and element stiffness matrix and geometric stiffness matrix have been derived. As a result, a calculating program has been written in this paper. By using this calculating program, the deck plate stress of control sections, displacement of girder, the section effective width and shear lag moment of a simply-supported deck-truss composite stiffening girder and a three-span continuous suspension bridge are calculated respectively and compared with the results calculated on the basis of shell finite element method. It can be found that the results calculated by the calculating program are basically consistent with that by adopting shell finite element method. Overall, the finite segment method established in this paper can be easily programmed and have wide applicability, which means this method is very suitable for engineering calculation.

finite segment method; integral orthotropic truss girders; plane thin-walled beam element; shear lag; large deformation

2016-12-05

李 磊(1983-)，男，山东新泰人，工程师，硕士，E-mail：160711446@qq.com。

TU311.41；U448.25

A

10.3969/j.issn.1671-234X.2016.04.003

1671-234X(2016)04-0013-06