几何约束条件下的SIFT倾斜影像匹配

闫　利，叶志云

(武汉大学测绘学院,湖北 武汉 430079)

Image Matching with SIFT for Oblique Photography under Geometry Constraint

YAN Li，YE Zhiyun



几何约束条件下的SIFT倾斜影像匹配

闫利，叶志云

(武汉大学测绘学院,湖北 武汉 430079)

Image Matching with SIFT for Oblique Photography under Geometry Constraint

YAN Li，YE Zhiyun

摘要：针对倾斜摄影包含多个视角的影像因而使不同视角之间的影像具有较大的仿射畸变的问题，提出了一种基于几何约束和SIFT的倾斜影像匹配算法。首先根据POS值对所有的倾斜影像进行畸变校正，然后利用SIFT GPU对所有影像进行匹配。对于整个测区的影像，首先根据POS值获取影像间的拓扑关系，其次是影像之间的两两匹配，最终完成特征点追踪，生成光束法平差所需的同名点对。试验结果表明，该算法在效率、精度及匹配点数量上都可以很好地满足后续的光束法平差。

关键词：仿射纠正；尺度不变；特征点追踪

目前，在数字城市的建立过程中，倾斜摄影被越来越广泛地采用[1-7]。相对于传统的垂直航空影像，倾斜影像存在着地物分辨率变化大、旋转、几何变形大、地物遮挡等特点[8]，传统的空三处理软件匹配算法一般是基于灰度或不抗仿射的特征的匹配算法，应用于倾斜航空影像时成功率和可靠性会大大降低，甚至失败。从文献[9—10]也可以看到倾斜影像快速匹配问题尚未得到很好的解决，极大地限制了该技术的实际应用。

针对倾斜影像的成像特点，匹配算法必须满足仿射不变、尺度不变、旋转不变性。传统的摄影测量一般采用C Heipke提出的基于金字塔模型的相对定向策略[11]，并在每一层上使用相关系数匹配和核线约束，但是考虑到倾斜和垂直影像仿射变化比较大，一般考虑使用抗仿射的特征匹配算法，匹配分为特征点检测与特征点描述两个过程。K Mikolajczyk分别对Harris-Affine、Hessian-Affine、MSER等6种具有仿射不变特征的检测算法在不同的场景下进行了比较，并没有哪一种算法在任何场景或仿射类型下完全优于其他算法，但是大多数情况下MSER的表现优于其他算法[12-13]；虽然K Mikolajczyk评测的算法都具有很强的抗仿射性，但是这些算法没有考虑倾斜摄影测量中影像具有初始外参，即仿射矩阵初值是已知的，导致以上相关算法的时间复杂度非常大。文献[14—16]围绕如何消除相关窗口之间的仿射变形，提出了相关的倾斜影像匹配算法，首先利用仿射变换矩阵近似影像局部区域之间的对应关系并进行仿射变形改正，然后在几何变形改正后邻域上完成相关系数匹配算法，最终利用最小二乘匹配获取子像素精度，但基于灰度的相关系数匹配算法不具有尺度不变性与旋转不变性，对于倾斜影像不同分辨率的同一地物也不能有效地完成匹配，并且局部的仿射纠正也增加了算法的复杂度。文献[17]针对仿射变换参数的变化幅度与景深的变化幅度呈正相关，即针对倾斜影像地面分辨率变化大的特点，提出了通过划分仿射近似平面以准确求取同名区域的仿射变换矩阵，算法对于倾斜影像的匹配是有效的，但同样存在时间复杂度的问题。基于特征的匹配算法一般可以满足尺度不变与旋转不变性，如果能将仿射纠正与特征匹配结合起来，就可以获得满足倾斜匹配要求的算法，从而提高算法的鲁棒性。

综上所述，本文提出了一种适用于倾斜影像的基于几何约束的SIFT匹配算法，算法既满足了仿射不变，又满足了尺度不变与旋转不变性，分为2个阶段：①根据POS数据对倾斜影像进行仿射纠正；②SIFT匹配与特征点精化。

另外，传统的构建航带法是先将影像构成航带，再利用人工选取的若干个航带偏移点建立相邻航带间的近视空间变换关系。为了获得较好的变换关系，这种方式需要选取数目较多的人工点。本文将利用POS数据来全自动获取任意两张影像间的重叠关系，在后面的空中三角测量中不再存在航带的概念，而是利用P Moulon提出的快速无序的特征点追踪完成多度重叠特征点的生成[18]，从而完成整个测区的影像匹配。

一、 算法

整个测区的匹配过程主要分为3个阶段：①对所有倾斜影像进行仿射纠正；②影像SIFT匹配，并将纠正后的影像匹配坐标换算到原始影像上；③特征点追踪，获取多度重叠点。影像仿射纠正和SIFT匹配阶段都采用GPU实现，可以节约匹配时间，主要流程如图1所示。

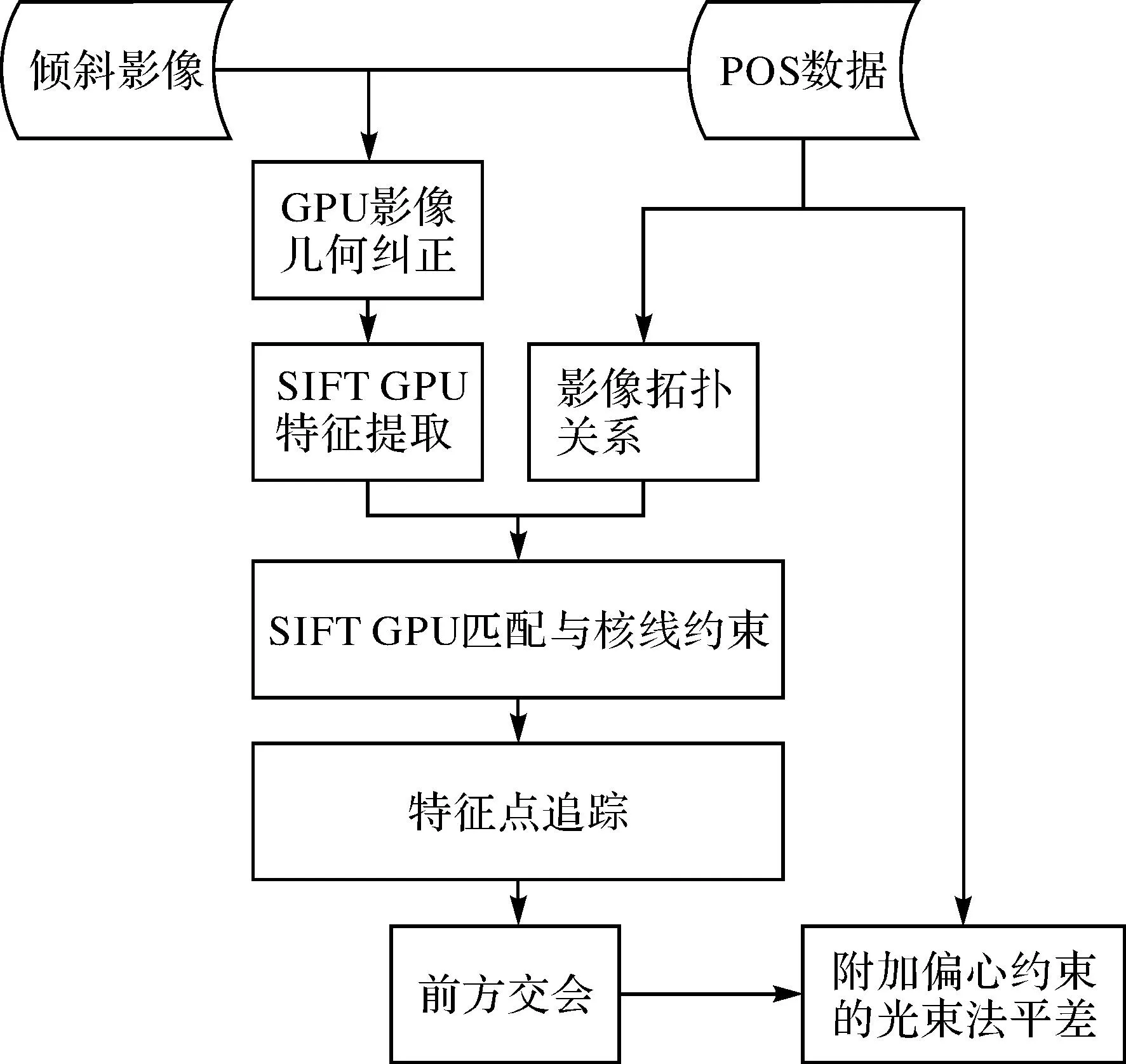
图1　影像匹配主要流程

1. 影像整体仿射纠正

倾斜影像可以获得地物多个角度的影像，影像整体仿射纠正就是为了减弱因为不同角度拍摄而造成的几何变形。这里需要提供影像的POS外参数与飞行航高，通过飞行航高估算近似地面高。具体步骤如下：

1) 根据地面高和POS，将影像4个顶点投影到地面，获取投影四边形。

2) 求得投影四边形的矩形凸包，根据垂直影像的地面分辨率划分凸包格网，并计算四边形顶点在凸包中的坐标。

3) 根据4个投影顶点在凸包中的坐标与顶点在影像中的坐标，计算凸包平面和影像平面间的单应矩阵，根据单应矩阵将影像重采样到矩形凸包上。

经试验表明，经过以上仿射纠正后，SIFT算法可以很好地对纠正后的影像完成匹配。为了提高纠正的效率，可以采用GPU实现。

2. 影像SIFT匹配与RUNSAC约束

SIFT算法的实质是在不同的尺度空间上查找关键点(特征点)，并计算出关键点的方向。SIFT所查找到的关键点是一些十分突出，不会因光照、仿射变换和噪音等因素而变化的点，如角点、边缘点、暗区的亮点及亮区的暗点等。SIFT稳健匹配分解为如下步骤：

1) 构建尺度空间：生成高斯金字塔与高斯差分金字塔。

2) 尺度空间极值检测与消除边缘响应：搜索所有尺度上的图像位置。通过高斯微分函数来识别潜在的对于尺度和旋转不变的兴趣点。

3) 关键点定位：在每个候选的位置上，通过一个拟合精细的模型来确定位置和尺度。关键点的选择依据它们的稳定程度。关键点定位后通过在离散空间点插值得到连续空间极值点，最终获得子像素精度的极值点坐标。在关键点精确定位后通过单应矩阵计算出在原始倾斜影像上的极值点坐标。

4) 方向确定：基于图像局部的梯度方向，给每个关键点位置分配一个或多个方向。

5) 关键点描述生成：在每个关键点周围的邻域内，在选定的尺度上测量图像局部的梯度。这些梯度被变换成一种表示，这种表示允许比较大的局部形状的变形和光照变化。

6) 描述符匹配：利用POS获得任意两两影像间的重叠关系，在重叠率超过30%的影像间完成SIFT匹配，计算比较最近邻距离与次近邻距离的距离比率,距离比率小于某个阈值的则认为是正确匹配。

7) 基于基础矩阵的RUNSAC约束：通过对匹配点的重复抽样不断估计基础矩阵，选取最大的一致集，如果最大一致集大于阈值，则保留，并且将所有的外点剔除。

研究表明，经仿射纠正、SIFT匹配与RUNSAC约束剔除粗差点后，无论是同方向的影像还是不同角度拍摄的影像之间都可以获得大量的同名点对。为了提高匹配效率，可使用GPU实现SIFT匹配，由于仿射纠正后的影像一般较大，若GPU的显存不足，可以采用分块提取特征点与特征描述符。

3. 特征点追踪，获取多度重叠点

特征点追踪是为了在两两匹配的同名点对结果的基础上，找出同名点的多视对应。特征点追踪问题可以看作是动态连通性类问题，使用到了一种叫作并查集的数据结构，称为Union-Find。主要思想是将所有SIFT匹配出的特征点看作是一个连通图的节点，同名点对之间是连通的。详细步骤如下：

1) 将特征点编号。

2) 查询节点属于的组，数组对应位置的值即为组号。

3) 判断两个节点是否属于同一个组，分别得到两个节点的组号，然后判断组号是否相等。

4) 连接两个节点，使之属于同一个组，分别得到两个节点的组号后，组号相同时操作结束；不同时，将其中的一个节点的组号换成另一个节点的组号。

经试验证明，特征点追踪的算法效率非常高。

二、试验与结果分析

1. 试验数据

为了验证上述方法的有效性，选取了一套河津测区的倾斜数据作为试验数据。数据包含5条航带，每条航带36或37个测站，每个测站包含5个方向的影像，共计905张影像，整个测区数据的叠拼图如图2所示。选取了3张影像样片如图3所示，像片大小为5616×3744像素。

图3　倾斜和垂直影像样片

2. 试验结果

试验中的倾斜影像分为两组：第一组为垂直影像ER_0692和倾斜影像BR_0694；第二组为两张倾斜影像BR_0694和DR_0688。试验中只针对在倾斜摄影中具有较大仿射畸变的影像匹配，第一组两张影像的拍摄角度约为35°，第二组两张影像的拍摄角度为70°，两组数据都是倾斜影像匹配中的典型样例，对于同方向拍摄的影像匹配结果基于篇幅就不再给出。试验步骤如下：

1) 对两张倾斜影像BR_0694和DR_0688进行仿射纠正，纠正结果如图4所示。

图4　倾斜样片纠正

2) 对两组影像对分别进行基于几何约束的SIFT匹配，RUNSAC剔除粗差点，两组数据的最终匹配结果如图5和图6所示。

图5　ER_0692-BR_0694匹配结果

图6　BR_0694-DR_0688匹配结果

3) 对以上的两两匹配结果进行特征点追踪，特征点追踪结果如图7所示。

图7　BR_0694-ER_0692-DR_0688的3°重叠点

算法程序使用VS2010实现，程序运行的平台为i7-CPU、GTX650显卡、8 GB内存。SIFT匹配采用GPU实现，由于影像较大，对影像采取分块处理。对两组匹配结果进行基础矩阵估计，计算同名点距离核线的距离v，以v的中误差评价匹配的整体精度，计算公式为

式中，n为点数。两组影像的匹配结果统计及整体匹配精度见表1。对整个测区的影像进行匹配及特征追踪，匹配点对的最终统计结果与像点多度重叠状况统计见表2与图8。

3. 试验结果分析

由表1可知本文的匹配算法精度可以达到亚像素级别，且匹配效率高，对于两两匹配，同名点对在1000左右，3°重叠点的数目也较多。通过图5和图6还可知匹配点分布较为均匀，表明本算法能够应用于倾斜摄影匹配，即使两张影像存在较大的仿射畸变和尺度变化，算法也可以取得很好的匹配结果。

表1　两对倾斜影像匹配结果统计

表2　河津测区倾斜影像匹配结果统计

由图5—图7可知，倾斜匹配的同名点基本位于街道、绿地、屋顶等平地，这是因为仿射校正是将所有影像校正到水平面，只有与水平面平行的影像区域消除了相对于垂直拍摄而产生的仿射畸变。在地面和屋顶都有匹配点也说明了SIFT算法的尺度不变性。

由表2可知，整个测区在仅仅保留3°及以上重叠点时仍然能够保证每张影像平均约2000个匹配像点，每张像片最少有470个，最多有5121个，而部分影像的像点数少于1000也主要是因为影像位于测区边缘，和其他影像的3°以上重叠区域只占影像的1/3~1/2。每个加密点平均对应着5.5个像点，同时，由图8可知一个加密点最多对应47个像点，这说明提取的特征点都是非常稳定的。本文的算法是为了后续的光束法平差，匹配结果无论是从数量还是精度与效率来看显然是满足要求的。

图8　河津测区倾斜影像加密点对应像点的统计

三、结束语

倾斜影像主要用于建立数字城市，针对倾斜影像存在较大仿射畸变的问题，提出了基于几何约束和SIFT的匹配算法。该方法首先根据初始的外参对影像进行仿射纠正，然后利用SIFT对影像进行快速匹配，最后对特征点进行RUNSAC剔除与特征点追踪，获得了满足后续光束法平差的数量与精度要求的同名点对。试验结果表明，该算法是有效且高效的。

参考文献：

[1]HÖHLE J. Photogrammetric Measurements in Oblique Aerial Images[J]. Photogrammetrie, Fernerkundung, Geoinformation, 2008 (1): 7-14.

[2]RUPNIK E, NEX F, REMONDINO F. Oblique Multi-Camera Systems——Orientation and Dense Matching Issues[J]. ISPRS International Archives of the Photogrammetry, Remote Sensing and Spatial Information Sciences, 2014, 1(1): 107-114.

[3]PECHATNIKOV M, SHOR E, RAIZMAN Y.The New Vision Map A3 Airborne Camera System[C]∥Proc. 52nd Photogrammetric Week. Stuttgart: [s.n.], 2009:99-109.

[4]KISA A, OZMUS L, ERKEK B, et al. Oblique Photogrammetry and Usage on Land Administration[J]. ISPRS International Archives of the Photogrammetry, Remote Sensing and Spatial Information Sciences, 2013, 1(2): 161-165.

[5]PECHATNIKOV M, SHOR E, RAIZMAN Y. Visionmap A3——Super Wide Angle Mapping System Basic Principles and Workflow[C]∥21st ISPRS Congress. Beijing： [s.n.], 2008.

[6]GRENZDÖRFFER G J, GURETZKI M, FRIEDLANDER I. Photogrammetric Image Acquisition and Image Analysis of Oblique Imagery[J]. The Photogrammetric Record, 2008, 23(124): 372-386.

[7]HÖHLE J. Oblique Aerial Images and Their Use in Cultural Heritage Documentation[J]. ISPRS International Archives of the Photogrammetry, Remote Sensing and Spatial Information Sciences, 2013, 1(2): 349-354.

[8]KARB O N, SCHROTH R. Oblique Aerial Photography: A Status Review[C]∥Photogrammetric Week. Stuttgart:[s.n.], 2009.

[9]WIEDEMANN A, MORÉ J. Orientation Strategies for Aerial Oblique Images[J]. ISPRS International Archives of the Photogrammetry, Remote Sensing and Spatial Information Sciences, 2012(1): 185-189.

[10]朱庆,徐冠宇,杜志强,等. 倾斜摄影测量技术综述 [EB/OL]. [2012-06-07].中国科技论文在线.

[11]LIANG T, HEIPKE C. Automatic Relative Orientation of Aerial Images[J]. Photogrammetric Engineering and Remote Sensing, 1996, 62(1): 47-55.

[12]MIKOLAJCZYK K, TUYTELAARS T, SCHMID C, et al. A Comparison of Affine Region Detectors[J]. International Journal of Computer Vision, 2005, 65(1-2): 43-72.

[13]MIKOLAJCZYK K, SCHMID C. A Performance Evaluation of Local Descriptors[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2005, 27(10): 1615-1630.

[14]杨化超，姚国标，王永波.基于SIFT的宽基线立体影像密集匹配[J].测绘学报,2011，40(5):537-543.

[15]杨化超，王永波，姚国标，等.基于SVD和SIFT的宽基线立体影像匹配[J].中国矿业大学学报,2011(6): 964-968.

[16]袁修孝,明洋.POS 辅助航带间航摄影像的自动转点[J].测绘学报,2010,39(2):156-161.

[17]姚国标，邓喀中，杨化超，等,基于几何约束的倾斜立体影像匹配[J]. 中国矿业大学学报, 2013(4): 676-682.

[18]MOULON P, MONASSE P. Unordered Feature Tracking Made Fast and Easy[C]∥The 9th European Conference on Visual Media Production. [S.l.]: CVMP, 2012.

引文格式： 闫利，叶志云. 几何约束条件下的SIFT倾斜影像匹配[J].测绘通报，2016(1)：37-40.DOI:10.13474/j.cnki.11-2246.2016.0009.

通信作者：叶志云

作者简介：闫利(1966—)，男，教授，研究方向为摄影测量与遥感。E-mail:lyan@sgg.whu.edu.cn

收稿日期：2014-11-18

中图分类号：P23

文献标识码：B

文章编号：0494-0911(2016)01-0037-04