利用Lunar Prospector Doppler数据解算并分析月球重力场
黄昆学,常晓涛,孙 玉
(1. 武汉大学测绘学院,湖北 武汉 430079; 2. 国家测绘地理信息局卫星测绘应用中心,北京 100830;
3. 代尔夫特理工大学,荷兰 代尔夫特)
Using Lunar Prospector Doppler Data to Recover and Analyze
Lunar Gravity Field
HUANG Kunxue,CHANG Xiaotao,SUN Yu
利用Lunar Prospector Doppler数据解算并分析月球重力场
黄昆学1,常晓涛2,孙玉3
(1. 武汉大学测绘学院,湖北 武汉 430079; 2. 国家测绘地理信息局卫星测绘应用中心,北京 100830;
3. 代尔夫特理工大学,荷兰 代尔夫特)
Using Lunar Prospector Doppler Data to Recover and Analyze
Lunar Gravity Field
HUANG Kunxue,CHANG Xiaotao,SUN Yu
摘要:Doppler技术可高精度测定卫星之间的距离变化率,可以和其他技术联合用于月球卫星定轨。本文利用Lunar Prospector月球项目4个月的Doppler跟踪数据,解算了75阶次月球重力场模型。首先介绍了数据预处理方法、力模型的使用及参数设置等关键技术,然后把解算的重力场模型与同阶次的其他月球重力场模型进行比较,可以看出低阶位系数较LP75G月球重力场模型稍差,但高阶位系数精度有所提高,可能是仅利用了低轨单星数据的原因。
关键词:Lunar Prospector;月球重力场;Doppler;数据解算
Lunar Prospector(LP)是美国NASA的月球探索任务,卫星于1998年1月6日发射升空,经过一系列调整之后进入月球极地近圆轨道。LP绕月轨道被设计为过两极的圆轨道,轨道高度设计为100 km,运行速度约为5517 km/h,运行周期为118 min。LP的设计初衷是用于探测、研究月球全球构成等,重点是探测南极水冰和分析月球的重力场及磁场。为完成不同的科学任务,LP任务分成3个阶段。正常任务阶段从卫星进入月球轨道至1999年1月,历时1年。其轨道为极地圆轨道,平均高度为100 km[1]。之后,LP进入短暂的过渡阶段,平均轨道高度为40 km。过渡阶段的主要任务是验证轨道预测的能力,为其后的扩展任务阶段做准备。LP扩展任务阶段开始于1999年1月29日,直到7月31日撞击月球表面为止,平均轨道高度约为30 km。采用较低的环月轨道是为了得到高精度、高分辨率的月球重力场模型。
美国JPL已经利用LP数据研制了一系列高精度、高阶次月球重力场模型,包括LP75D、LP75G、LP100J、LP100K、LP150和LP165等[2-3]。此外,也有学者利用GEODYN和SOLVE软件处理了公布在PDS上的LP Doppler跟踪数据,从而实践了月球重力场解算技术流程。文献[4]利用正常任务阶段数据模制了75阶月球重力场模型。也有学者利用扩展任务阶段数据,以LP100J为初始重力场模型解算了100阶月球重力场模型。但上述文献主要介绍了基本解算原理和方法,均未涉及LP数据预处理等具体信息。本文详尽介绍了数据预处理方法、力模型的使用及参数设置等关键技术,然后对解算的重力场模型进行了比较分析。
一、数据处理方法和流程
本文所采用的数据来自美国PDS的LP轨道数据文件(ODF)。该数据文件包含美国深空网(DSN)对LP的Doppler跟踪观测数据,包括距离变率(测速)和距离(测距)两种数据。距离变率数据采样间隔为10 s,精度较高(约为0.3 mm/s);距离数据采样间隔为33 s,精度平均约为0.5 m。由于最终要使用GEODYN Ⅱ软件处理观测数据,因此需要将ODF中的数据记录转换为GEODYN Ⅱ可识别的格式。首先根据数据格式说明文件TRK-2-18将ODF由二进制文件转为ASCII文件。ODF中的距离变率数据以Hz为单位,距离数据则以range unit(RU)为单位,为了使其符合GEODYN Ⅱ对于数据格式的特殊要求,需要按下式将二者单位分别转换为m/s和m
Doprate=0.5×C/(T×Fref)×Dopfreq
(1)
Doprange=0.5×C/(FRU×Fref)×Doprange
(2)
式中,C表示光速;T为转换器上下行信号比,S波段应取为240/221;Fref为基准频率,可由数据文件中读取,其值接近于2093 MHz;FRU取值为0.5。由于ODF实际上为Ramp格式数据,其基准频率通常是随时间线性变化的。但在实际计算过程中,注意到绝大部分情况下基准频率的变率实际上为零,因此可以将其作为普通的Doppler数据来处理,即基准频率为常量。
本文研究所采用的卫星定轨及大地参数解算软件为GEODYN Ⅱ和SOLVE。GEODYN Ⅱ软件主要由3部分构成,即TDF、IIS和IIE。TDF是格式转换器,能够将某种数据记录转换为GEODYN II可处理的格式。但由ODF转换得到的ASCII数据记录格式仍然不能被TDF识别,因此需要利用程序再次进行转换。经过TDF转化后,观测数据文件的格式变为GEODYN II binary格式,该格式可以被GEODYN II所识别。根据情况进行弧段划分(Arc1,Arc2,…,Arcn)。由于月球背面存在重力信息空白,轨道弧段不宜过长,一般取为2 d。还要注意同一弧段中不应包括对卫星的人工操作,即卫星机动的时间段应排除在连续弧段之外。上述数据预处理过程如图1所示。SOLVE严格意义上应该属于GEODYN Ⅱ的一部分,其主要功能是进行矩阵求逆运算。图1中的ReadODF与Trans2TDF为数据格式转换程序。

图1 LP 数据预处理流程
二、月球重力场模型解算
本文解算使用1998年1月11日至5月1日正常任务阶段约4个月的Doppler跟踪双程、三程数据,所使用的LP数据稍多于LP75G(3个月)。解算流程如图2所示,图2中Ematrix表示法方程矩阵。所采用的力学模型、星历及参数设置等见表1。用于解算GLGM2的数据主要来自轨道高度约为200km的Clementine任务。以该模型作为初始重力场模型对LP进行轨道积分时,显然精度不够,即使积分弧段为2d仍然会导致部分弧段不收敛。对于不收敛的弧段,先缩短其积分长度直至收敛[5-6]。利用所有积分弧段解算重力场模型,将更新后的重力场模型作为先验重力场模型替换GLGM2[7-12]。更新后的重力场模型包含LP探测的重力场信息,可使所有2d积分弧段均收敛。
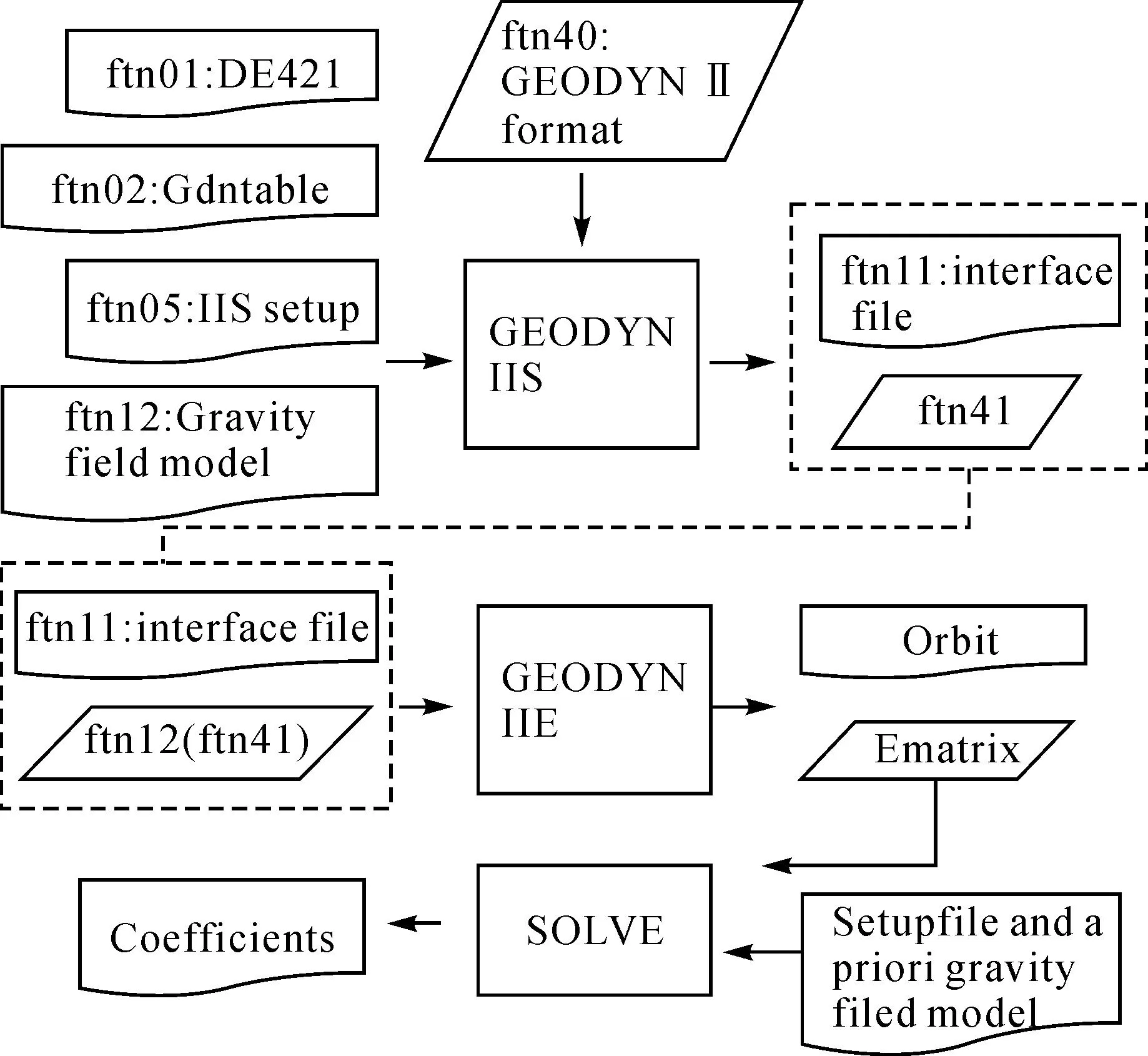
图2 利用GEODYN II和SOLVE解算月球重力场位系数的具体流程及所需文件
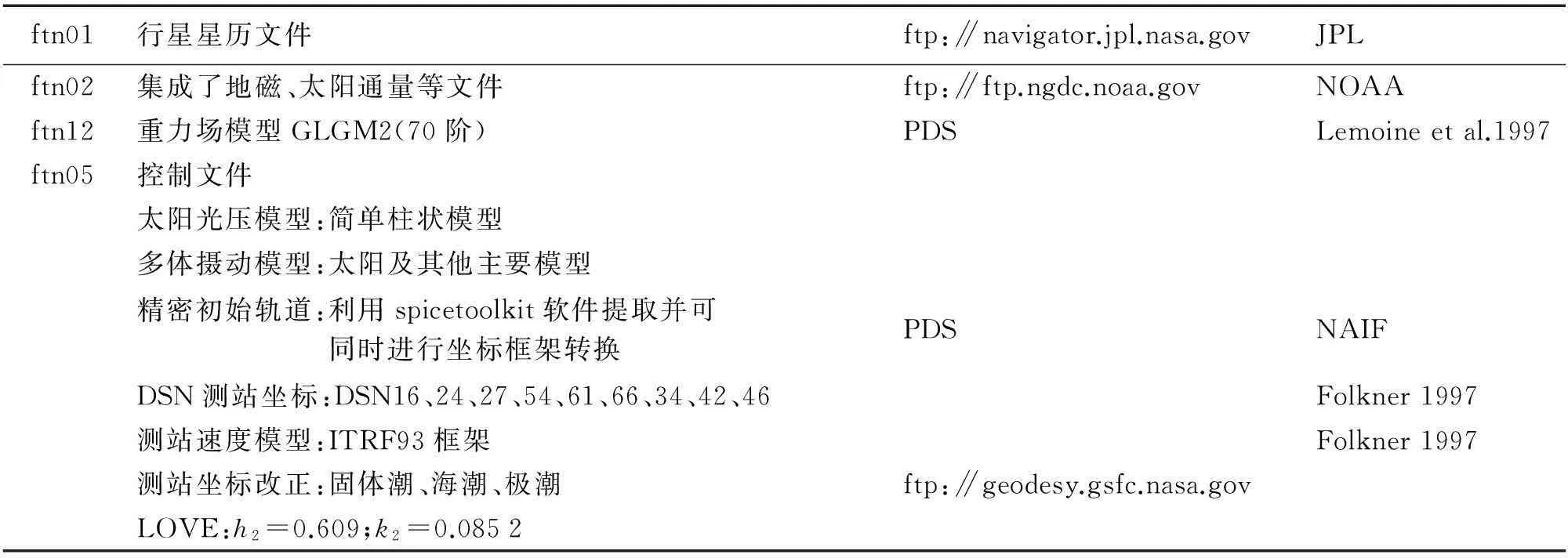
ftn01行星星历文件ftp:∥navigator.jpl.nasa.govJPLftn02集成了地磁、太阳通量等文件ftp:∥ftp.ngdc.noaa.govNOAAftn12重力场模型GLGM2(70阶)PDSLemoineetal.1997ftn05控制文件太阳光压模型:简单柱状模型多体摄动模型:太阳及其他主要模型精密初始轨道:利用spicetoolkit软件提取并可同时进行坐标框架转换 PDSNAIFDSN测站坐标:DSN16、24、27、54、61、66、34、42、46Folkner1997测站速度模型:ITRF93框架Folkner1997测站坐标改正:固体潮、海潮、极潮ftp:∥geodesy.gsfc.nasa.govLOVE:h2=0.609;k2=0.0852

续表1
首先,根据所选初始力模型(月球重力场模型、三体摄动模型、太阳光压模型等)对LP轨道进行数值积分;然后便可得到线性观测方程,该观测方程建立了观测数据(距离、距离变率数据)与重力场位系数、初始状态向量等未知参数之间的函数关系,并可形成法方程矩阵(Ematrix);最终利用SOLVE对该法方程矩阵求逆,便可得到待求参数[13-14]。
三、模型分析
LPD75的模型阶方差曲线与LP75G比较接近(如图3所示),但在低阶次(7~20阶)出现了明显误差,这在其误差阶方差曲线中也体现了出来。主要原因是由于GLGM2及LP75G都融合了多个历史探月任务的数据,而本文解算的LPD75仅利用了LP的Doppler跟踪数据,所恢复的月球重力场模型低阶位系数精度较差。图4显示了LPD75和LP75G模型与月球地形模型STM359_grid-03的相关性。LPD75与地形的相关性在前50阶次与LP75G相比总体上略差,50阶次以上则优于LP75G。显然,轨道较低(正常任务阶段月100 km)的LP任务对月球重力场短波信息较为敏感,所增加的一个月的LP数据,有助于提高模型高阶位系数的精度,但对50阶以下的重力场位系数没有改进。

图3 模型阶方差及误差阶方差
由LPD75解算的月球自由空气重力异常 (如图5(a)所示)、月球大地水准面起伏(如图6(a)所示)与LP75G(如图5(b)、图6(b)所示)可以看出,两个模型的差别主要集中在月球背面和极区。LPD75的高频噪声明显少于LP75G。

图4 重力场模型与地形模型相关性

图5 月表自由空气重力异常及其差值
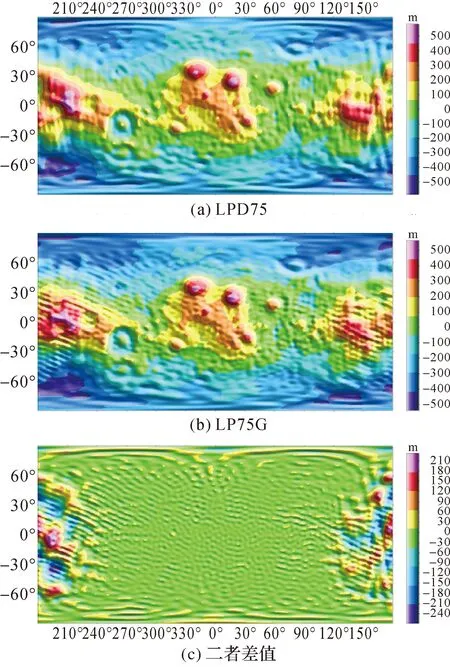
图6 月球大地水准面起伏及其差值
四、结束语
本文基于LP Doppler数据,利用GEODYN Ⅱ和SOVLE软件解算了月球重力场模型,得到了合理可靠的结果,验证了数据处理、软件使用的正确性。文中重点说明了其他学者忽略的LP数据预处理方法和过程,详细阐述了月球重力场解算的流程,给出了必要文件及参数设置信息。除LP数据预处理过程外,文中所述GEODYN Ⅱ与SOLVE的解算过程均为通用过程,对于其他任务和类型的数据,只需要进对预处理过程和控制文件(ftn05)作相应改动即可,可对今后利用GEODYN Ⅱ和SOLVE软件进行月球重力场模型解算提供有借鉴。
参考文献:
[1]BINDER A B. Lunar Prospector: Overview [J]. Science, 1998, 281(5382): 1475-1476.
[2]KONOPLIV A S, BANERDT W B, SJOGREN W L. Venus Gravity: 180th Degree and Order Model [J]. Icarus, 1999, 139(1): 3-18.
[3]KONOPLIV A S, ASMAR S W, CARRANZA E, et al. Recent Gravity Models as a Result of the Lunar Prospector Mission [J]. Icarus, 2001, 150(1): 1-18.
[4]GOOSSENS S, MATSUMOTO K. Lunar Satellite Orbit Determination Analysis and Quality Assessment from Lunar Prospector Tracking Data and Selene Simulations [J]. Advances in Space Research, 2007, 40(1): 43-50.
[5]丰海,李建成,李大炜,等.月球Airy均衡状态与月壳厚度估计[J]. 测绘学报,2012 ,41 (4): 543-548.
[6]PING J S, HUANG Q, YAN J G, et al. Lunar Topographic Model Cltm-s01 from Chang’e-1 Laser ALtimeter [J]. Science in China Series G: Physics Mechanics and Astronomy, 2009, 52(7): 1105-1114.
[7]罗志才,李琼,钟波. 利用GRACE时变重力场反演黑河流域水储量变化[J]. 测绘学报,2012,41 (5): 676-681.
[8]GUO J Y, SUN Y, CHANG X T,et al. Lunar Deflections of the Vertical and Their Distribution [J]. Natural Science, 2011, 3(5): 339-343.
[9]ARAKI H, TAZAWA S, NODA H, et al. Lunar Global Shape and Polar Topography Derived from Kaguya-LALT Laser Altimetry [J]. Science, 2009, 323(5916): 897-900.
[10]李森,安智明. 克里金模型在区域重力数据插值中的应用[J]. 测绘通报, 2013 (10): 63-66.
[11]MAZARICO E, LEMOINE F, HAN S C et al. GLGM-3: A Degree-150 Lunar Gravity Model from the Historical Tracking Data of NASA Moon Orbiters [J]. Journal of Geophysical Research, 2010(115): E05001.
[12]FOLKNER W M, WILLIAMS J G, BOGGS D H. The Planetary and Lunar Ephemeris de 421 [J]. IPN Progress Report, 2008:172-178.
[13]曹金国,王建斌,戴山岭. 重力场扰动位泰勒展开式低阶项应用研究[J].测绘通报,2014(1):54-55.
[14]GOOSSENS S, MATSUMOTO K. Lunar Satellite Orbit Determination Analysis and Quality Assessment from Lunar Prospector Tracking Data and Selene Simulations [J]. Advances in Space Research, 2007, 40(1): 43-50.
引文格式: 黄昆学,常晓涛,孙玉. 利用Lunar Prospector Doppler数据解算并分析月球重力场[J].测绘通报,2016(1):19-22.DOI:10.13474/j.cnki.11-2246.2016.0005.
作者简介:黄昆学(1985—),男,博士生,主要研究方向为月球重力场解算。E-mail:shulang2003@163.com
基金项目:国家自然科学基金 (41204007); 国家高技术研究发展计划(2013AA122502); 国家重点基础研究发展计划(2013CB733302); 中国地质调查局地质调查工作项目(12120113019100)
收稿日期:2014-11-25; 修回日期: 2015-10-16
中图分类号:P228
文献标识码:B
文章编号:0494-0911(2016)01-0019-04

