轴对称悬滴法液体表面张力实验系统

张小龙，吕　萍，赵贯甲

(太原理工大学 电气与动力工程学院 热能系，山西 太原 030024)



轴对称悬滴法液体表面张力实验系统

张小龙，吕萍，赵贯甲

(太原理工大学 电气与动力工程学院 热能系，山西 太原 030024)

摘要：研制了悬滴法液体表面张力测量系统，该系统包括图像采集系统、耐高压实验本体和温度控制系统等. 悬滴图像信息由高分辨率的CMOS相机采集，并利用Canny算法进行边缘检测，进而提取悬滴边界并进行坐标变换，以获取悬滴的轮廓坐标，采用坐标轮换法与Newton法结合实现悬滴边界的全轮廓拟合计算. 实验系统的温度范围和温度波动度分别为：20~180 ℃，±0.01 ℃；压力范围为：0~20 MPa. 为了检验系统的可靠性和精确性，测量了正庚烷在温度范围为293.15~373.15 K的表面张力. 通过不确定度分析，测量流体表/界面张力的相对不确定度为0.22%.

关键词：表面张力；悬滴法；正庚烷

表面张力是流体力学中重要的热物理性质之一，对流体界面传热、传质以及微缩通道的流动、传热均有重要影响. 常用实验测量方法主要有：毛细上升法、吊环/片法、最大气泡压力法、悬滴法、表面光散射法等. 其中，悬滴法具有测定范围广、精度高、样品用量少、浸润性要求低等优点，尤其适用于高温高压下液体表/界面张力的测量[1-2].

悬滴法测量液体表/界面张力的关键点在于如何利用液体悬滴的轮廓信息求解其理论方程并获得液体的表/界面张力. 目前，主要有2种数据处理的方法：一是选择平面法；二是轴对称悬滴法. Andreas等[3]在前人工作的基础上，通过进一步的分析与研究提出了选择平面法. 选择平面法选取液滴轮廓上2个关键位置处截面的半径，并将两者的比值作为悬滴轮廓的形状因子，通过对形状因子的数据分度表进行差值计算获得液体的表面张力，此方法在数据采集过程中会引入较大的误差. Rotenberg等[4]将采集到的悬滴轮廓线与理论廓线进行非线性拟合，这种方法即为轴对称悬滴法(Axisymmetric drop shape approach，ADSA)，也称为全轮廓拟合方法. 此方法将目标函数定义为悬滴轮廓与理论廓线上对应点之间法向距离的平方和，同时将悬滴顶点坐标作为变量参与到最优化计算中，减小了拟合偏差. 随着计算机和数字图像技术的快速发展，ADSA中悬滴轮廓线的采集和拟合计算可以完全实现数字化，并由计算机程序来控制和求解复杂的拟合算法，提高了悬滴法测量液体表/界面张力的自动化程度和测量精度. 艾芳洋等[5]在对悬滴法表面张力实验原理研究的基础上，在C++语言平台下开发了全轮廓拟合算法程序并研制了悬滴法表面张力实验系统.

国内学者在采用悬滴法进行表/界面张力的实验研究时[6-7]，数据处理大多采用选择平面法，实验精度低. 本文在Matlab平台上编写了悬滴全轮廓拟合计算的程序，并研制了包含实验本体、温度控制系统和图像采集系统在内的悬滴实验平台，实现了液体表/界面张力的高精度测量.

1实验原理

悬滴法的测量原理基于以下2个假设：一是液滴仅在表面张力和重力的合力作用下处于静平衡状态；二是液滴具有轴对称的外形轮廓. 如图1所示[8]，以悬滴顶点为坐标原点，该点处的切线为x轴，悬滴轮廓的对称轴为z轴，建立平面直角坐标系. 设悬滴轮廓上任意一点P的坐标为(x1，z1)，P点处切线与x轴的夹角为θ，P点相对于坐标点的弧长为s1，则悬滴模型可以用无量纲化的一阶微分方程组表示：

图1　悬滴法示意图

(1)

其中：σ为表面张力，R1和R2分别为P点的第一和第二曲率半径，R0为原点处的曲率半径，Δρ为界面两相的密度差，g为重力加速度，z为P点距离参考平面的铅垂高度. 由悬滴顶点处的弧长为0，可得方程组(1)的边界条件为

x(0)=z(0)=θ(0)=0 .

(2)

(3)

当E取得最小值时，即可求得β和R0，进而获取液体的表/界面张力.

2全轮廓拟合算法

图2所示为采集到的25 ℃时正庚烷的悬滴图像，采用Canny算法对悬滴图像的边界进行提取，如图3所示. 图4所示为提取到的悬滴边界的局部放大示意图.

图2　悬滴图像

图3　悬滴边界提取

图4　悬滴边界局部放大示意图

最优化计算前，首先要对提取获得的悬滴边界坐标进行坐标变换和尺度变换，具体做法可参见相关文献[5]. 式(3)所示的目标函数E简化为关于形状因子β和悬滴顶点处曲率半径R0的二元函数. 因此，对目标函数E的最优化计算可归结为二维的无约束最优化问题. 本文基于坐标轮换法的思想并结合Newton法对关于β和R0的目标函数进行了最优化求解，在保证计算精度的同时兼具了较高的稳定性和计算速度. 计算时，首先给定β和R0的初值，然后固定R0不变，对β进行一维寻优，在寻得β的最优解后，将其作为定值，并采用Newton法对R0进行最优化计算. 如此不断循环，直到目标函数E<ζ(其中ζ为给定的收敛条件). 具体的计算流程如图5所示.

图5　最优化计算流程图

3实验系统

为了获得稳定的悬滴图像，实验系统的各组成元件均置于高精度气垫式光学隔震平台上.如图6所示，实验系统由图像采集系统、实验本体、温度控制系统和悬滴形成系统等组成. 图7所示为实验系统实物图.

光源选用艾菲特光电技术有限公司生产的LED白色冷光源(型号为AFT-BL50). 该光源发热量低，且光照强度均匀、平行度较好，适宜作为图像采集系统的光源. 相机选用艾菲特公司生产的像素为1 400万的CMOS相机(型号为MV-1400UC)，同时配置相应的放大镜头(型号为ZML-1024). 该镜头的可调倍率范围为0.1 ~ 0.4，其视场范围可达到3.3 mm×4.4 mm~9.3 mm×12.4 mm. 对于绝大部分的悬滴，6.0 mm×8.0 mm的视窗足以将其全部容纳，可根据实际情况调节镜头的放大倍率，以保证采集到的悬滴图像具有锐利的边缘和足够的像素.

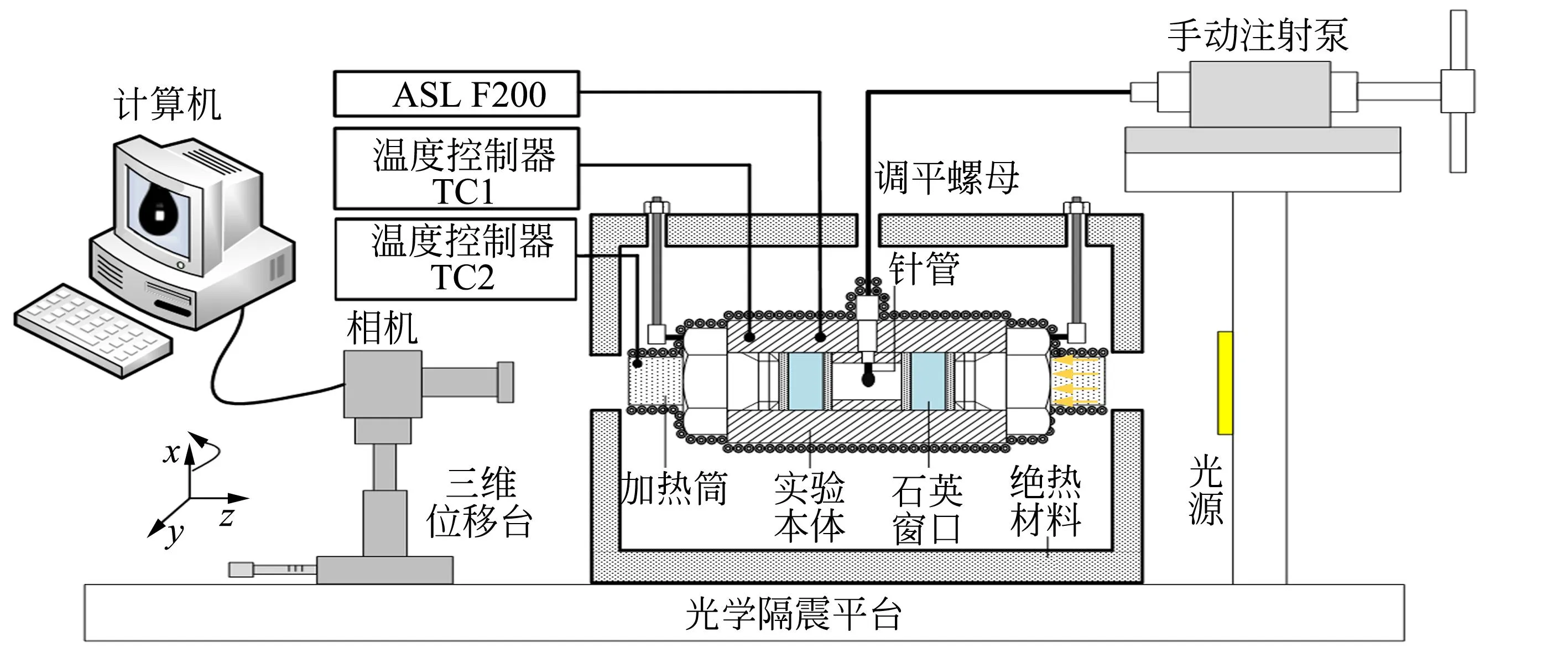
图6　实验系统示意图

图7　实验系统实物图

实验本体材料为316不锈钢，设计承压范围为0~20 MPa，如图8所示，两端设计有法兰结构的石英观察窗，规格为25 mm×25 mm. 装置两侧采用氟素橡胶O型圈配合法兰进行密封. 图9所示为实验本体安装加热丝外壳和加热筒.

实验本体通过螺纹杆悬至于环氧树脂保温箱体内部，并利用调平螺母调节本体的高度和水平，从而使本体内部的针管处于铅垂位置并在相机视野的中心. 温度控制方式为电加热分段控制，在实验本体的非观察面上均匀缠绕电加热丝并利用

Fluke 2100温度控制器控制本体的温度，图10所示为Fluke 2100高精度温度控制器. 同时为防止在升温的过程中窗口结雾，在观察窗两侧加装加热筒，并控制加热筒的温度高于本体温度约5~10 ℃. 实验系统的温度范围为20~180 ℃，温度波动度好于±10 mK.

图8　实验本体

图9　实验本体(装加热丝)

图10　Fluke 2100温度控制仪

图11　ASL F200测温仪

实验本体的温度采用ASL F200高精度温度测量仪测量，如图11所示，全量程测温的不确定度为±10 mK，标定过的Pt100温度计的不确定度为±5 mK. 因此，实验系统的温度扩展不确定度为±30 mK(k=2). 悬滴形成系统主要包括针管、管路和手动注射泵. 其中针管的材料为316不锈钢，要求针头部分端口平整，外径规格为(1.610±0.005) mm，内径为0.30 mm，通过螺纹结构紧固于实验本体. 手动注射泵与实验本体之间通过管路以NPT方式连接，泵体容积为12.5 mL，设计承压的范围为0~5 MPa. 实验系统设计承压达到5×106Pa，对于大多数沸点较低的液体，本文所述系统的优势在于不受物质沸点的影响，可以实现沸点温度以上的表/界面张力的测量.

4实验方法

1)实验前应对实验本体、针头、管路和手动注射泵等进行仔细地反复清洗. 首先用丙酮溶液进行浸泡，再用酒精进行反复清洗，最后用去离子水在超声波清洗机中恒温60 ℃清洗90 min. 清洗完成的各实验部件采用高压空气吹干后备用.

2)组装各实验部件，并将加热丝外壳加装在本体外表面，加热线的接线端与温度控制器相连接，将铂电阻及温差电偶线固定在本体的相应位置处. 连接完成后，将实验装置吊装在箱体内.

3)采用一次性医用注射器将待测液注入到手动注射泵内，并将其固定在实验平台的相应位置处，通过NPT管路将实验本体与注射泵连接.

4)调节固定在本体两端的4组调平螺母对实验本体的位置进行调整，使针头铅垂，悬滴图像基本处于视场的最中央为宜. 然后，调整CMOS相机的焦距，直到悬滴图像清晰可见，轮廓锐利分明. 应在视场中保留2~3 mm的针头，实验时随悬滴图像一同被采集，作为拟合计算的标尺.

5)实验开始时，控制温度达到预设的温度点，并稳定在1 h以上，待温度波动平稳之后，控制注射泵进样成滴，以悬滴外形达到最大为宜. 形成悬滴之后稳定温度在30 min以上，再开始采集悬滴图像. 每组实验共采集30张图像数据(时间间隔为2 s)，拟合计算并取平均值作为最后的实验结果.

5结果与讨论

5.1　实验样品及实验数据

正庚烷由阿拉丁公司提供，纯度为99%. 表1为实验测得的正庚烷表面张力数值. 计算所使用的气液相密度ρ′和ρ数据均取自NIST REFPROP 9.0[10]. Δσ为30次测量值的标准偏差.

表1　正庚烷表面张力实验数据

将正庚烷表面张力数据拟合为Van De Waals形式：

(4)

其中:T的单位为K，正庚烷的临界温度Tc=540.13 K，拟合值σ0=52.984 mN·m-1，n=1.236. 本文实验值与方程拟合值的最大相对误差为0.29%，平均相对误差为0.14%.

如图12所示，利用本文正庚烷表面张力数据拟合得到的方程与大多数文献的实验值相对误差基本在-1%~2%之间. 赵贯甲[9]利用光散射法测量了正庚烷的表面张力，测量温度范围为293.03~402.98 K，本文方程与其在温度为293.03~373.07 K之间，最大相对误差不超过0.085%，最小相对误差0.008 6%，平均相对误差0.038%. 同时，本文数据与Wadewitz[11]和Jasper[12]数据吻合得较好，与Stephan[13]，Vargaftik[14]和Shengshan[15]数据相对误差较大，最大相对误差为3.57%. 可以看出Vargaftik的数据相对于其他文献数据存在很明显的随温度变化的系统相对误差. 综上所述，除了少数文献值偏大于本文方程，绝大多数文献的数据点与本文方程相对误差均不超过±1%.

□本文数据；○文献[10]数据；△文献[11]数据；　　▽文献[12]数据；◁文献[13]数据；▷文献[14]数据；　☆文献[15]数据；◇文献[16]数据；+文献[9]数据图12　正庚烷表面张力与文献值比较

5.2　相对不确定度分析

实验系统的测量相对不确定度由以下误差传递公式估计：

(5)

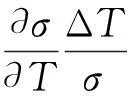
综上所述，本文系统测量表面张力的相对不确定度为0.22%.

6结束语

搭建了用于测量表面张力的高精度悬滴法实验系统，实验系统包括图像采集和处理、温度控制、悬滴形成以及耐高压实验本体. 利用参考物质正庚烷对实验系统进行了检验，结果表明本文测量值与文献值的相对误差绝大部分都在±1%之内. 不确定度分析表明，系统的扩展测量相对不确定度为0.22%，可以满足液体表面张力的高精度测试要求.

参考文献：

[1]王海涛，伦增珉，骆铭，等. 高温高压条件下CO2/原油和N2/原油的界面张力[J]. 石油学报，2011，32(1)：178-180.

[2]Arashiro E Y, Demarquette N R. Use of the pendant drop method to measure interfacial tension between molten polymers [J]. Materials Research, 1999,2(1):23-32.

[3]Andreas J M, Hauser E A, Tucker W B. Boundary tension by pendant drops [J]. Journal of Physical Chemistry, 1938,42(8):1001-1019.

[4]Rotenberg Y, Boruvka L, Neumann A W. Determination of surface tension and contact angle from the shapes of axisymmetric fluid interfaces [J]. Journal of Colloid and Interface Science, 1983,93(1):169-183.

[5]艾芳洋,毕胜山,吴江涛. 全轮廓拟合悬滴法表面张力实验系统[J]. 物理实验,2015,35(5):1-6.

[6]李啸风，陈志荣，潘海华，等. 结合图像数字化技术用悬滴法测动态界面张力——动态界面张力与表面活性剂浓度的关系[J]. 化工学报，2001，52(6)：545-548.

[7]赵海龙,刘大顺，陈效鹏. 一种基于数字图像的表面张力测量方法一悬滴法[J]. 实验力学，2010，25(1)：100-105.

[8]赵贯甲. 表面光散射法黏度和表面张力实验系统研制及应用[D]. 西安：西安交通大学，2013.

[9]Song B, Springer J. Determination of interfacial tension from the profile of a pendant drop using computer-aided image processing: 1. Theoretical[J]. Journal of Colloid and Interface Science, 1996, 184(1):64-76.

[10]Lemmon E W， Huber M L， McLinden M O. REFPROP 9.0 [CP]. Boulden，Colorado：NIST，2010.

[11]Wohlfarth Ch, Wohlfarth B. Surface Tension of Pure Liquids and Binary Liquid Mixtures[M]. Berlin: Springer, 1997.

[12]Jasper J J, Kring E V. The isobaric surface tensions and thermodynamic properties of the surfaces of a series ofn-alkanes, C5to C18, 1-alkenes, C6to C16, and ofn-decylcyclopentane,n-decylcyclohexane andn-dcylbenzene [J]. Journal of Physical Chemistry, 1955,59(10):1019-1021.

[13]Stephan K, Hildwein H. Recommended data of selected compounds and binary mixtures[M]. Frankfurt:Dechema, 1987.

[14]Vargaftik N. Dictionary of thermophysical properties of gases and liquids [M]. Moskva: Izd. Nauka, 1972.

[15]Bi S S, Zhao G J, Wu J T. Surface tension of diethyl ether, diisopropyl ether, and dibutyl ether [J]. Journal of Chemical & Engineering Data, 2010,55(4):1523-1526.

[16]Abdulagatov I M, Adamov A P, Abdurakhmanov I M. Surface tension coefficient of the n-pentane+ n-heptane system near the “liquid-gas” critical point[J]. Journal of Engineering Physics and Thermophysics, 1992,63(6):1193-1198.

[17]Aguila-Hernández J， Hernández I， Trejo A. Temperature dependence of the surface tension for binary mixtures ofn-butanenitrile plusn-alkanes[J]. International Journal of Thermophysics，1995，16(1)：45-52.

[责任编辑：尹冬梅]

Pendent-drop apparatus for accurate

determination of liquid surface tension

ZHANG Xiao-long， LÜ Ping， ZHAO Guan-jia

(Department of Thermal Energy Engineering, College of Electrical and Power Engineering,

Taiyuan University of Technology, Taiyuan 030024, China)

Abstract:A pendent-drop apparatus, consisting of image acquisition, pressure vessel, temperature control and liquid drop gerneration systems was developed to accurately determine the liquid surface tension. A CMOS digital camera was adopted to capture and process the image of the liquid drop. The edge of the image was then detected by Canny operator and fitted to the theoretical equation of liquid drop with Matlab to obtain the surface/interfical tension. The pressure vessel, its temperaturethe was well controlled in the range from 20 ℃ to 180 ℃ with a stability better than 0.01 ℃, could work under the pressure up to 20 MPa. The surface tension of heptane was measured in the temperature range from 293.15 K to 373.15 K and a good agreement was achieved with literature. The relative uncertainty was better than 0.22%

Key words:surface tension； pendent-drop method； heptane

中图分类号：O552.421

文献标识码：A

文章编号：1005-4642(2016)01-0014-07

通讯作者：吕萍(1957-)，女，浙江东阳人，太原理工大学电气与动力工程学院副教授，硕士，主要从事热工质物性研究和传热技术研究.

作者简介：张小龙(1988-)，男，山西宁武人，太原理工大学电气与动力工程学院2013级硕士研究生，研究方向为热物性测试技术.

基金项目：国家自然科学基金资助(No.51506140,No.51306127)

收稿日期：2015-08-31；修改日期：2015-10-22