基于贝叶斯决策法的城市地震应急决策研究
翟丹妮,左静璇,刘光浩
(1.南京邮电大学 管理学院,江苏 南京 210023;2.南京邮电大学 贝尔英才学院,江苏 南京 210023)
基于贝叶斯决策法的城市地震应急决策研究
翟丹妮1,左静璇1,刘光浩2
(1.南京邮电大学 管理学院,江苏 南京 210023;2.南京邮电大学 贝尔英才学院,江苏 南京 210023)
贝叶斯决策法是最常见的以期望为标准的分析方法。传统贝叶斯方法的基本原理是,在不完全情报下,对部分未知的状态用主观概率估计,利用贝叶斯公式对发生概率进行修正,最后根据修正概率和期望值做出最优决策。贝叶斯方法直接应用于城市地震应急决策时存在两个问题:将灾害事件作为单一事件考虑及直接计算不同地震级别下各方案的效用。为提高决策的科学性,文中对贝叶斯方法进行改进,将修正过的后验概率与次生灾害处于不同级别的概率相结合,得到更精确的概率;并将各方案的效用分解为各方案对次生灾害的子效用,进行综合后得到总效用,由此计算出的总效用更精确、具体。将改进后的方法应用于地震应急决策,通过算例分析得出最优方案,说明了该方法的有效性和实用性。
应急决策;贝叶斯决策法;效用函数;地震
1 概 述
我国是全世界地震灾害最严重的国家之一。20世纪全世界发生的7级以上的强震中,中国占了35%[1]。城市是人类社会进步的产物,与农村相比,城市具有空间的集中性,人口的密集性,经济结构的多样性、聚集性、开放性和社会活动的广泛性及基础结构的完善性,因而地震灾害更为严重,抵御地震的能力更为脆弱,后果更具有全局性[2]。只有震后及时采取有效的应急响应方案,并按照方案开展应急救援活动,才能将损失降到最低[3]。贝叶斯决策法是一种成熟的多元判定决策方法,常用于解决多方案选优及风险性决策问题[4-6],适用于地震等灾害应急决策中的方案选优。
基于贝叶斯理论的决策方法在各个领域都有应用,例如,贝叶斯决策法是分析现代证券价格波动模式的重要手段。杨胜刚等[7]以贝叶斯决策准则为框架,通过引入不确定效应和信息扩散因素,重新诠释了信息冲击下的证券市场过度反应特征;袁瑞英[8]将贝叶斯决策法应用于上市公司风险预警实证研究;孙丽娜等[9]将贝叶斯决策法应用于安全检查领域中固体爆炸物识别问题的研究,给出了基于最小错误概率的贝叶斯决策理论的判别函数、决策方程以及分类判别规则;在电力、机械领域,针对设备状态维修时机不明确的问题,刘念等[10]提出了一种利用贝叶斯理论对设备所处状态进行修正的决策模型。
随着贝叶斯决策法在各个领域取得的成功应用,将其与灾害分析及应急相结合的研究方向逐渐引起相关学者的注意。例如,张锦等[11]在划分应急子区域的基础上,引入贝叶斯风险决策理论,建立起码头核应急贝叶斯决策模型,进行多方案选优;同样是应急决策中的多方案选优问题,丁继勇等[12]将贝叶斯方法与博弈论的内容相结合,将灾害发生过程中不断调整应急方案的过程近似地看作“暴雨内涝”与“决策组”动态博弈的过程,基于贝叶斯决策法提出应急方案动态生成方法。并且贝叶斯模型已被证明可以对地震灾害等突发性自然灾害的主体和客体进行风险评估和应急决策支持。Benjamin首先提出将贝叶斯模型用于地震的发生过程,随后很多学者从不同角度发展了这个模型(Lomnitz、Cornell、Estevα、MeGoire、Cαmpbell),此外Mortgat和Shah提出了危险分区的贝叶斯模型[13];刘在涛等[14]将贝叶斯方法用于地震应急响应等级的判断,以震级、震区人口密度等相关信息为依据,建立起地震应急响应等级的判别规则。
但以上研究都把灾害事件作为单一事件去考虑,存在计算出的概率不够精确的问题。文中针对这一问题,对贝叶斯方法在应急决策中的应用提出两点改进,由此得到更精确的贝叶斯后验概率,提高决策的科学性、合理性。
2 贝叶斯方法的基本原理
进行任何决策时都需要对事件的未来发展状态进行估计,但是很多事件的发生发展带有不确定性,事前的预测不能保证完全正确,但又带有一定的规律性,所以如何根据事前的预测来估计事件未来的发展状态,是很常见的一种预测需求。贝叶斯决策法可以做到这一点。贝叶斯决策法是最常见的以期望为标准的分析方法,是在不完全情报下,对部分未知的状态用主观概率估计,然后用贝叶斯公式对发生概率进行修正,最后再利用期望值和修正概率做出最优决策[13]。它的基本原理如下所述。
2.1 事件概率的推算
任何事件的发生都具有一定的概率(即先验概率),这个可以根据事件发生过的历史记录进行统计得到。用θi表示某个事件状态,p(θi)表示该状态发生的先验概率。
常常会邀请专家对于事件的发展进行预测,专家虽然在某领域内具有丰富的经验,但是对于事件的估计未必每次都正确。当事件的未来状态是θi时,专家可能把它估计为某个状态τj,这个估计有可能是正确的,也有可能是错误的。将事件在实际状态为θi的情况下,专家做出不同估计的概率记为p(τj/θi),称作条件概率。
但对于决策者而言,更希望知道的是,当专家预估事件状态为τj时,事件的实际状态为θi的概率会有多大。这个概率用p(θi/τj)表示,称为后验概率,可以通过贝叶斯公式计算得到:
(1)
2.2 贝叶斯决策法与效用函数的结合
贝叶斯方法用于应急决策时,通常与效用函数结合使用。效用函数是用于计算备选方案的效果、效用、价值的函数,其决策步骤如下:
(1)准备备选方案。
假设某类事件按严重程度分为几种状态,事先准备多个备选的救援方案,在不同事件状态下各备选方案的效用不同,如表1所示。

表1 某城市不同地震级别θj实施方案αi的效用表
其中,U(θj/αi)表示地震级别为θj时实施方案αi的效用。
(2)计算后验概率。
在对应急方案进行选择时,并不知道事件处于哪种状态,这时需要借助贝叶斯方法对专家推断的主观概率用式(1)进行修正,得到事件处于不同级别下的后验概率。
(3)计算各方案的期望效用。
根据效用表及上一步得到的后验概率分别计算出各方案的期望效用。
(4)得出决策结果。
期望效用最高的备选方案就是决策结果。
3 贝叶斯方法的不足之处
3.1 将灾害事件作为单一事件来考虑
传统的贝叶斯方法用于应急决策时,通常把灾害事件作为一个整体来看待,其实往往是多个灾害事件同时出现,某次灾害(主事件)可能导致其他灾害(子事件),主事件处于不同级别时子事件的概率是不同的,不能一概而论。
因此,为了提高决策的科学性,应当同时考虑某次灾害(主事件)及其导致的次生灾害(子事件)。不同级别的主事件的发生有个概率,在某个主事件下不同级别的子事件的发生也有概率,决策者需要估计的是所有事件发生的概率,将主事件处于不同级别的发生概率与子事件的概率结合起来,才能得到更精确的概率。
3.2 直接计算不同地震级别下各方案的效用
传统的贝叶斯方法中预估效用是对整个方案进行预估,实际一个救援方案中要包含针对各个子事件的应对措施。以往贝叶斯方法应用于地震应急决策的案例中,总是直接计算不同地震级别下各个方案的效用,由此得到期望效用。由于各方案对某次灾害导致的子事件的效用更易于确定,故将直接计算各方案的总效用改为计算针对各子事件的效用,进行综合后得到总效用,由此计算出的总效用更精确、更具体。
4 贝叶斯方法的改进思路
4.1 灾害事件的结构分析
城市地震导致的灾害包括直接灾害以及由直接灾害引起的次生灾害和衍生灾害,将后两种灾害统称为城市地震次生灾害,表示以震动的破坏后果为导因引起的一系列其他灾害[2]。由于城市的特殊性,地震发生后,最容易产生地震次生灾害。
次生灾害按照其严重程度可以分为几个等级,在不同的地震级别下,次生灾害处于各个级别的概率也不同。将地震处于不同级别的概率与次生灾害处于不同级别的概率相结合,就得到更精确的次生灾害的概率,此处称为子概率。
4.2 效用函数的扩展
由于各种状态下实施不同方案的效用难以确定,但实施不同方案对于地震次生灾害的效用是易于衡量和确定的,故此处可以将实施不同方案的效用分解成不同方案对各次生灾害的效用,此处称为子效用。假设各次生灾害之间没有相互关联,就可以通过计算子效用之和计算期望效用。
改进后的贝叶斯方法在地震应急决策中应用的大致思想描述如下:在地震发生初期,信息尚不完备时,应急指挥部门可以对地震处于不同级别的概率做出一个最初的假设,通过相关地震参数及震区背景信息初判响应等级,即先验概率;一旦搜集了信息和地震应急领域专家的知识,就会用贝叶斯公式对先验概率进行修正,新形成的这个概率即后验概率;将次生灾害按照其严重程度分级,根据历史数据可以得到不同状态下次生灾害处于不同级别的概率,将它们与贝叶斯公式计算出的后验概率p(θi/τj)相乘,就得到了子概率;由历史数据还可得到地震处于不同级别下采取不同方案对次生灾害的子效用,由此计算出实施不同方案的期望效用;最后利用效用函数和期望效用最大化原则选择出最合适的地震应急响应方案。
5 改进的贝叶斯方法在地震应急决策中的应用
将改进后的贝叶斯决策法应用到地震应急决策中,具体实施步骤分为五个,分别是:地震后验概率推算、次生灾害的子概率推算、次生灾害的子效用推算、期望效用推算、选择最优方案。
5.1 地震后验概率推算
(1)假设城市地震共分成m个阶段,第一阶段地震的可能状态用θi(i=1,2,3)表示,i=1,2,3时分别代表地震级别为1级、2级和3级。假设第一阶段有n个方案可供选择,用αi表示,i=1,2,…,n。
(2)应急决策部门事先不知道地震的具体级别θi,但知道地震属于级别θi的先验概率,假设应急决策部门判断地震处于级别θi时的先验概率为p(θi)(i=1,2,3)。
(3)通过对历史数据的收集得到一组条件概率,即实际的地震级别为θi时专家的判断为τj的概率p(τj/θi),专家的判断τj与实际地震级别θi相同时的概率为p(j=i)。
(4)再利用式(1),可得地震级别θi发生的后验概率,即专家判断地震级别为τj而实际地震级别为θi的概率p(θi/τj)。
5.2 次生灾害的子概率推算
对次生灾害按照其严重程度分级,记为βkn。其中,k表示次生灾害的数量,n表示次生灾害的级数。由历史数据可得到不同地震级别下次生灾害处于不同级别的概率,记为p(βkn),将其与地震后验概率相乘,即不同级别的次生灾害的子概率:p(θi/τj)p(βkn)。
5.3 次生灾害的子效用推算
由历史数据可得到采取不同方案对次生灾害的效用,即u(θim,τjm,αw,βkn),表示在第m阶段,地震级别为θi,专家判断为τjm,应急决策部门采取方案αw时次生灾害βkn的效用水平。用式(2)可求出应急方案αw对第k次生灾害的子效用:
(2)
例如,在地震第1阶段,级别为2级时,应急方案α1对第一个次生灾害的子效用为:
其中,m=1,i=2,k=1,ω=1。
5.4 期望效用推算
采取方案αw的期望效用就是采取该方案对所有次生灾害的子效用之和,用式(3)计算:
(3)
5.5 选择最优方案
按期望效用最大化原则选取方案,期望效用最大的即为最优方案。
6 算例分析
假设某一城市发生地震,地震的处理过程分为m阶段。地震级别大小决定了灾害的严重程度。按照各多震国家的建筑物标准,级别较小(Ⅷ度以下)的地震造成房屋严重破坏或者倒塌的可能性较小;级别过大(如Ⅻ度)则将造成毁灭性破坏,任何城市都无法承受。
出于以上因素的考虑,也为了方便读者理解和计算,文中只考虑级别为Ⅷ~Ⅺ度的地震,并将Ⅷ~Ⅸ度、Ⅸ~Ⅹ度、Ⅹ度以上的地震级别值分别记作1级、2级、3级。
假设第1阶段的应急响应方案有三个,分别为α1,α2,α3。地震级别处于1级,2级,3级分别用θ1,θ2,θ3来表示。假设应急决策部门判断地震处于3个级别的先验概率分别为:p(θ1)=0.2,p(θ2)=0.3,p(θ3)=0.5。设实际地震级别为θi时专家的判断为τj的条件概率p(τj/θi)的数值如表2所示。

表2 第一阶段条件概率p(τj/θi)的值
1)地震后验概率推算。
用式(1)计算出这三种状态的后验概率,结果如表3所示。
假设专家根据应急指挥部门收集到的信息,判断地震级别为2级,则由表2可知,3个状态的后验发生概率分别为0.16,0.46和0.38。
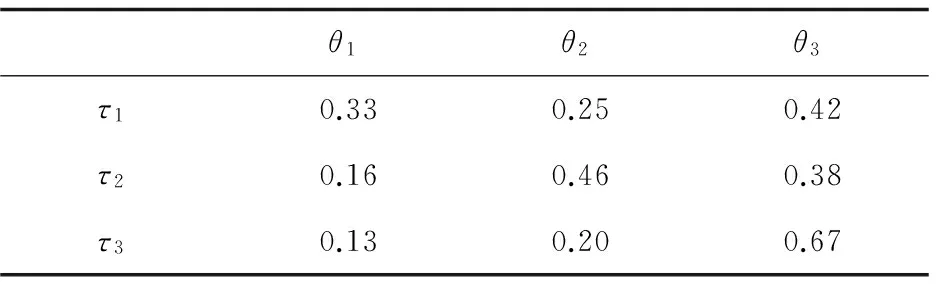
表3 第一阶段地震级别后验概率p(θi/τj)
2)次生灾害的子概率推算。
为了方便读者理解,简化计算,假设此次地震引发的次生灾害有三种,分别是建筑物倒塌、火灾和传染病。假设各次生灾害之间没有相互关联,按次生灾害的严重程度,将各个次生灾害按照以下标准分为几个等级,记为βkn(k=1,2,3,n=1,2,3,4)。
(1)建筑物倒塌:在此按照建筑物的倒塌量将其分为建筑物没有倒塌、倒塌了少数、倒塌了大部分和全部建筑物倒塌这四个级别,分别记为β11,β12,β13和β14。
(2)火灾:将火灾次数极少(10次以下)或者没有,记为β21,火灾次数多或发生大规模火灾,记为β22。
(3)传染病:在此将无传染病流行记为β31,发生传染性小、死亡率低的传染病记为β32,发生死亡率高的传染病记为β33。
假设在地震状态为2级的情况下,根据以往的经验和数据统计,建筑物倒塌处于四个级别的发生概率分别为0.1,0.5,0.15和0.25,火灾处于两个级别的概率为0.75和0.25,传染病处于三个级别的概率为0.3,0.4和0.3。将这组概率分别与地震发生的后验概率相乘,就可以得到在后验概率下建筑物倒塌、火灾及传染病处于四个级别的子概率。计算结果如表4所示。

表4 后验概率下建筑物倒塌、火灾、传染病的子概率
3)次生灾害的子效用推算。
假设在地震处于2级,三个次生灾害处于不同级别时,分别采用α1,α2,α3应急方案的效用如表5所示。
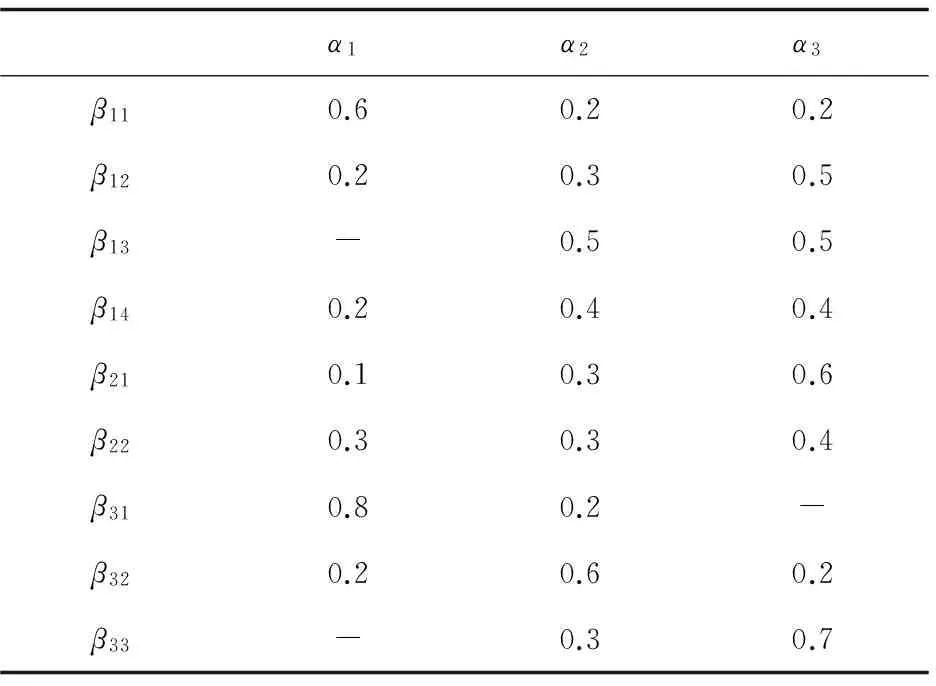
表5 三个应急方案对次生灾害的子效用
由式(2)可得到采取应急方案α1对建筑物倒塌、火灾和传染病的子效用分别是:U11=0.099 6,U12=0.069,U13=0.147 2;同理可得采取方案α2和α3的子效用,过程在此不再详述:U21=0.138,U22=0.179 4,U23=0.158 7;U31=0.253,U32=0.133 4,U33=0.204 7。
4)期望效用推算。
由式(4)可得到采取应急方案α1,α2,α3的期望效用分别为:
E1(U)=0.312 8,E2(U)=0.476 1,E3(U)=0.591 1
5)选择最优方案。
根据上述结果可知,改进后的贝叶斯方法对方案进行排序的结果是:方案3、方案2、方案1。期望效用最大的方案是α3,故方案3是最优方案。而传统贝叶斯方法得到的结果是:方案3、方案1、方案2。相比之下发生了变化。虽然最优方案的选择结果没有变,但用改进后更精确的概率和效用代入计算,发现方案2的排序后退,方案1的排序前移,证明对贝叶斯方法的改进是很有必要的。
7 结束语
文中对应用于城市地震应急决策的贝叶斯方法进行了扩展改进,用贝叶斯方法对地震处于各个级别的先验概率进行修正,与次生灾害概率相乘得到更精确的子概率,并将各个方案的效用分解成对次生灾害的效用,最后利用效用函数计算出实施各个应急方案的总效用,按期望效用最大化原则选择最优应急方案。
虽然扩展的贝叶斯方法克服了原有方法的缺陷,但为了简化计算,便于读者理解,文中假设案例中的三个次生灾害之间没有相互关联。而在次生灾害之间有复杂联系的情况下,应急响应方案的选择问题还没有得到准确的解答,需进一步调整后验概率的测算方式。这种情况下如何确定效用函数,也是亟待解决的问题。
[1] 马宗晋,杜品仁,高祥林,等.东亚与全球地震分布分析[J].地学前缘,2010,17(5):215-233.
[2] 宋利萍,张俊玲,柏 琳,等.城市地震成灾机制分析[J].高原地震,2005,17(2):38-43.
[3]JacobM,HellstromT.Policyunderstandingofscience,publictrustandtheBSE-CJDcrisis[J].JournalofHazardousMaterials,2000,78(3):303-317.
[4]BradleyR.AunifiedBayesiandecisiontheory[J].TheoryandDecision,2007,63(3):233-263.
[5]JiangX,MahadevanS.Bayesianrisk-baseddecisionmethodformodelvalidationunderuncertainty[J].ReliabilityEngineering&SystemSafety,2007,92(6):707-718.
[6]BayesT.Anessaytowardsolvingaprobleminthedoctrineofchances[J].PhilosophicalTransactionsoftheRoyalSocietyofLondon,1763,53:370-418.
[7] 杨胜刚,成 博.基于贝叶斯决策的证券市场过度反应[J].系统工程,2014(10):24-29.
[8] 袁瑞英.贝叶斯决策下上市公司风险预警实证研究[J].财会通讯,2014(8):112-113.
[9] 孙丽娜,杨 斌.基于贝叶斯决策理论的爆炸物识别方法[J].东北大学学报:自然科学版,2013,34(1):123-126.
[10] 刘 念,李建兰,陈 刚,等.基于贝叶斯理论的刀具维修决策模型[J].制造业自动化,2013,35(8):11-14.
[11] 张 锦,蔡 琦,张 帆,等.基于贝叶斯风险决策理论的码头核应急决策模型[J].辐射防护,2010(3):155-159.
[12] 丁继勇,王卓甫,郭光祥.基于贝叶斯和动态博弈分析的城市暴雨内涝应急决策[J].统计与决策,2012(23):26-29.
[13]ShahCH,鲍霭斌,董伟民.地震危险性分析中贝叶斯模型的意义及其应用[J].地震工程与工程振动,1982,2(4):1-16.
[14] 刘在涛,王栋梁,张维佳,等.基于贝叶斯判别分析的地震应急响应等级初判方法[J].地震,2011,31(2):114-121.
Study on Urban Earthquake Emergency Decision-making Based on Bayesian Decision Method
ZHAI Dan-ni1,ZUO Jing-xuan1,LIU Guang-hao2
(1.School of Management,Nanjing University of Posts and Telecommunications,Nanjing 210023,China;2.Bell Honors School,Nanjing University of Posts and Telecommunications,Nanjing 210023,China)
The Bayesian decision-making is commonly used analysis approach taking the expectation as the standard.The basic principle of the traditional Bayesian method is to estimate the probability of the occurrence of the unknown state with the subjective probability and to use the Bayesian formula to modify the probability of occurrence and make the optimal decision according to the modified probability and expected value.When Bayesian method is applied directly to the urban earthquake emergency decision making,there are some problems such as treating disaster event as a single event and calculating the utility of each solution directly under different earthquake levels.Therefore,it is needed to improve Bayesian method.Firstly,the modified posterior probability and probability of secondary disasters in different levels is combined to obtain more accurate probability.Then the utility of each solution can be decomposed into the sub utility of the secondary disasters.Consequently,the improved method is applied to the earthquake emergency decision making.It demonstrates that the modified method is effective and practical.
emergency decision;Bayesian decision method;utility function;earthquake
2015-08-14
2015-11-18
时间:2016-05-05
教育部人文社科项目(10YJC630365);江苏省高校哲社研究基地(产业信息安全与应急管理)重大招标项目(TJS211021)
翟丹妮(1973-),女,副教授,研究方向为应急管理、决策理论与方法;左静璇(1990-),女,硕士研究生,研究方向为应急管理、决策理论与方法。
http://www.cnki.net/kcms/detail/61.1450.TP.20160505.0829.082.html
C934
A
1673-629X(2016)05-0183-05
10.3969/j.issn.1673-629X.2016.05.040

