基于小波变换的改进软阈值图像去噪算法

李晓飞，邱晓晖

(南京邮电大学 通信与信息工程学院，江苏 南京 210003)

基于小波变换的改进软阈值图像去噪算法

李晓飞，邱晓晖

(南京邮电大学 通信与信息工程学院，江苏 南京 210003)

由于经典的小波阈值函数存在一定的缺陷，如硬阈值函数在阈值处不具有连续性，软阈值函数的小波估计系数和原系数之间存在着恒定的偏差，会导致去噪后的图像出现失真、产生吉布斯震荡等问题。文中综合典型的小波阈值函数的优点，并综合一些改进的方法，针对其缺点，提出了一种改进的阈值函数。该函数不仅在阈值处是连续的、小波估计的系数渐进原系数，并且具有可微性，易于实现梯度算法的自适应学习。为了验证该阈值函数的优越性，通过仿真实验对几种小波去噪方法的均方差(MSE)和峰值信噪比(PSNR)进行了对比。实验结果表明，用改进后的阈值函数进行去噪，无论是在视觉效果上，还是在均方差和峰值信噪比性能分析上均优于常用的阈值函数。

小波变换;图像去噪;小波阈值去噪;阈值函数;高斯噪声;均方差;峰值信噪比

0 引 言

图像在传输或者提取的时候,会受到各种各样噪声的污染，因此，会影响图像的质量和对图像的后续处理。故图像去噪是图像处理过程中一个必不可少的步骤。小波变换能同时在时频域中对信号进行分析，利用它进行图像去噪是小波变换的重要应用领域之一。1994年,DonohoDL和JohnstoneIM在小波变换的基础上提出了小波阈值去噪算法，在目前应用广泛[1-2]。但是由于典型的软、硬阈值函数都有相应的缺陷，硬阈值函数在阈值处不连续，而软阈值函数中估计的小波系数和带有噪声的小波系数之间存在着一个恒定的偏差，从而限制了小波阈值的进一步应用。文献[3-5]分别提出了三种不同的改进算法，这些改进算法也可以对典型软、硬阈值函数的缺点进行一定的改善，但是效果并不是很明显。

因而，文中结合经典的软、硬阈值函数的特点以及文献[3-5]中各阈值函数的优缺点，提出了一种更好的阈值函数。该函数不仅在阈值处连续、小波估计系数渐进原系数，并且易于计算。

1 小波阈值去噪的基本原理

小波变换具有比较好的数据去相关性，它可以使大部分能量集中在少量较大的小波系数上，而噪声的能量分布在整个小波域，对应着大量的较小的小波系数；即在小波域，有效信号对应的系数很大，而噪声对应的系数很小[6-8]。故可以选取合适的阈值对小波系数进行截断处理，将绝对值小于阈值的小波系数都置为零，而将大于阈值的小波系数保留或者予以适当收缩，得到估计后的小波系数，然后对估计的小波系数进行重构，最后可以得到去噪后的信号[9]。

小波阈值去噪过程可以分为3步：

第一步：对噪声图像进行小波变换，选择合适的小波基和小波分解层数,将含噪图像进行小波分解,得到相应的小波分解系数；

第二步：根据设定的阈值和阈值函数对信号进行去噪处理；

第三步：对处理过的小波系数进行小波逆变换，得到去噪后的估计信号。

1.1 小波阈值函数

(1)硬阈值函数：保留大于阈值的系数，把小于阈值的系数都置为零。

该阈值函数的表达式为：

(2)软阈值函数：把大于阈值的系数减去阈值的大小，把小于阈值的系数置零，表达式为：

软阈值函数去噪后得到的小波系数的整体连续性较好，但它的缺陷是，当系数超过设定的阈值后，小波系数的估计值和原系数之间有恒定的偏差，这将直接影响重构的信号与真实信号的逼近程度；硬阈值函数去噪虽然在均方误差意义上比软阈值函数要有优势，但是它在阈值处不连续，得到的估计信号会产生一定的附加震荡，光滑性不是很理想[11]。

1.2 改进的阈值函数

针对典型的软、硬阈值函数的缺点,文献[3-5]分别提出了不同的阈值函数，它们都在一定程度上改善了软、硬阈值函数的缺点，对含噪图像的处理都有一定的效果。文中根据经典的软、硬阈值函数和文献[3-5]的启发构造了一种新的阈值函数：

改进的小波阈值函数的数学分析如下：

(1)连续性分析。

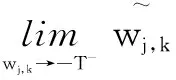
(2)渐进性分析。

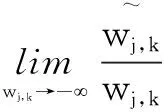
2 仿真实验及结果分析

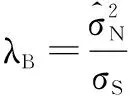
图1为friendgray的仿真实验图。

为了更好地验证文中提出的新阈值函数的去噪效果，下面用均方差(MeanSquaredError,MSE)和峰值信噪比(PeakSignal-to-NoiseRatio,PSNR)进行图像去噪后的效果分析。MSE的值越小，说明图像的质量越好，而PSNR的值越大，说明图像的质量越好[13]。定义式分别为：

图1 friendgray的仿真实验图

PSNR=10×lg(2552/MSE)

通过仿真实验得到的实验数据如表1所示。

表1 降噪后各图像的MSE和PSNR对比

通过表1的数据可知，改进阈值函数的去噪效果比传统的软、硬阈值及文献[3-5]中改进的阈值函数的去噪效果好。

3 结束语

文中综合典型的小波阈值函数的优点，并结合一些改进的方法，提出了一种改进的阈值函数。通过仿真实验对几种小波去噪方法的MSE和PSNR进行了对比。结果表明，用该函数进行去噪，无论是在视觉效果上，还是在均方差和峰值信噪比性能分析上均优于常用的阈值函数。

[1]DonohoDL.Adaptingtounknownsmoothnessviawaveletshrinkage[J].JournalofAmericanStatisticalAssociation,1995,90:1200-1224.

[2]DonohoDL.De-noisingbysoft-thresholding[J].IEEETransonIT,1995,41(3):613-627．

[3] 王 蓓，张根耀，李 智，等．基于新阈值函数的小波阈值去噪算法[J]．计算机应用，2014，34(5)：1499-1502．

[4]CuiHuimin，ZhaoRuimei,HouYanli．Improvedthresholddenoisingmethodbasedonwavelettransform[C]//Procofinternationalconferenceonmedicalphysicsandbiomedicalengineering.[s.l.]:[s.n.],2012:1354-1359．

[5]LingDC,SamsudinA,AbduliahR.Aestheticmeasuresforassessinggraphicscreens[J].JournalofInformationScienceandEngineering,2000,16:97-116．

[6] 张 平，高义中．工业设计的色彩量化处理[J]．南京理工大学学报:自然科学版，1998，22(5)：407-411．

[7] 叶重元，黄永东.小波阈值去噪算法的新改进[J]．计算机工程与应用，2011,47(12)：141-145．

[8] 王 可,余隋怀,乐万德,等．面向计算机辅助工业设计的色彩设计系统[J]．计算机辅助设计与图形学学报，2004，16(10)：1425-1429．

[9]ChangSG,YuB,VetterliM.Adaptivewaveletthresholdingforimagedenoisingandcompression[J].IEEETransactionsonImageProcessing，2000,9(9):1532-1546.

[10] 刘成云，陈振学，马于涛.自适应阈值的小波图像去噪[J]．光电工程，2007,34(6)：77-81．

[11] 吴芳平，狄红卫.基于Curvelet变换的软硬阈值折衷图像去噪[J]．光学技术，2007，33(5)：688-690．

[12]BruceAG，GaoHongye．Waveshrinkandsemisoftshrinkage[J]．StatisticsSinica，1997，7(4)：855-874．

[13] 邢丹俊，王继成.基于提升小波的自适应阈值图像去噪[J]．计算机技术与发展，2008,18(2)：42-45．

AnImprovedSoft-thresholdImageDenoisingAlgorithmBasedonWaveletTransform

LIXiao-fei,QIUXiao-hui

(CollegeofCommunicationandInformationEngineering,NanjingUniversityofPostsandTelecommunications,Nanjing210003,China)

Astheclassicalwaveletthresholdingfunctionhascertaindefects,forexample,thehardthresholdfunctionisnotcontinuousatthethreshold,andthereisconstantdeviationbetweentheoriginalcoefficientforsoft-thresholdfunction,whichcancauseimagedistortionafterdenoisingandproducetheproblemsuchasGibbsphenomena.Animprovedthresholdfunctionbasedontheadvantagesofthetypicalwaveletthresholdingfunctionandcombinedsomeimprovedmethodsisproposed.Thefunctionisnotonlycontinuousatthethreshold,theestimatedwaveletcoefficientsapproachingtheoriginalcoefficient,butalsodifferentialandeasytorealizetheadaptivelearningofgradientalgorithm.Inordertoverifythesuperiorityofthethresholdingfunction,throughthesimulationexperiment,theMeanSquareError(MSE)andPeakSignal-To-NoiseRatio(PSNR)fromseveralwaveletdenoisingmethodsarecompared.Accordingtotheexperimentalresults,thisproposedmethodhasbetterinvisualeffectandperformanceanalysisforMSEandPSNRthanthetraditionalthresholdfunctions.

wavelettransform;imagedenoising;waveletthresholddenoising;thresholdfunction;Gaussiannoise;MSE;PSNR

2015-07-03

2015-10-15

时间：2016-03-22

江苏省自然科学基金(BK2011789)；东南大学毫米波国家重点实验室开放课题(K201318)

李晓飞(1989-)，女，硕士研究生，通信作者，研究方向为智能信号处理、数字图像处理；邱晓晖，教授，研究方向为现代信号中的智能信号处理。

http://www.cnki.net/kcms/detail/61.1450.TP.20160322.1519.050.html

TP

A

1673-629X(2016)05-0076-03

10.3969/j.issn.1673-629X.2016.05.016