广义贝叶斯字典学习K-SVD稀疏表示算法

周飞飞，李 雷

(南京邮电大学 理学院，江苏 南京 210023)

广义贝叶斯字典学习K-SVD稀疏表示算法

周飞飞，李 雷

(南京邮电大学 理学院，江苏 南京 210023)

稀疏字典学习是一种功能强大的视频图像稀疏表示方法，在稀疏信号处理领域引起了广泛关注。K-SVD算法在稀疏表示技术上取得了巨大成功，但遇到了字典原子未充分利用的问题，而稀疏贝叶斯字典学习(Sparse Bayesian Dictionary Learning,SBDL)算法存在稀疏表示后信号原子不稀疏和不收敛的缺点。广义贝叶斯字典学习(Generalized Bayesian Dictionary Learning,GBDL) K-SVD算法提供了一种新型稀疏表示系数更新模式，使得过完备字典稀疏学习算法逐步收敛的同时训练向量足够稀疏。仿真结果表明，对有损像素和压缩传感这两种视频图像帧进行稀疏化，GBDL K-SVD算法表示的视频图像帧的重构效果与SBDL K-SVD算法相比有明显的提高。

稀疏贝叶斯学习；视频图像稀疏表示；字典学习；K-SVD算法

0 引 言

近年来，信号的过完备字典[1]稀疏表示已成为重要的科研议题并引起了广泛的研究和讨论。信息时代下的信息获取和处理方法已然成为一个是重要的议题。现实世界中，信息采样技术已成为数字信息和沟通的重要桥梁，高维数据的稀疏表示是机器学习和计算机视觉领域[2]所关注的一个热门话题。它的基本设想是自然图像本身是稀疏信号，也就是说，当使用一组过完备基来线性表示输入信号时,获得的对应系数被认为是输入信号在某一稀疏条件下的良好逼近。这些稀疏表示方法在压缩传感、图像去噪、视频稀疏编码、特征提取等重要应用中取得了巨大的成功。过完备特性意味着它所拥有的原子个数大于原子的维度，一组基信号的过完备集合的目标是用字典原子的稀疏组合线性地表示输入信号。过完备字典的最大优点是在有噪环境或退化信号条件下的鲁棒性，更重要的是，它在字典中引入更多种形式导致了输入信号的各种不同稀疏表示。

过去几年中，要提出最好的稀疏表示方式是一个被广泛研究的困难议题[3]。K-SVD算法[4]是一种迭代算法，优化迭代步骤分为两步：样本稀疏编码，这是基于固定的字典原子；其次是更新字典原子，使该字典更好地适应数据。稀疏贝叶斯字典学习(Sparse Bayesian Dictionary Learning,SBDL)算法是基于稀疏表示信号的最大后验(Maximum A Posteriori,MAP)，它可以加入K-SVD算法的第一步来改善过完备学习词典的自适应性。文中提出一种广义稀疏贝叶斯字典学习(Generalized Bayesian Dictionary Learning，GBDL)算法来扩展和修改SBDL算法的缺陷，证明了改进算法的可行性和有效性。

1 稀疏贝叶斯字典学习K-SVD算法综述

1.1 K-SVD算法

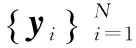
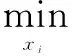
(1)

其中：‖•‖2为矩阵的2-范数；T0为稀疏表示系数向量中的非零元素的最大个数。

首先是K-SVD稀疏编码阶段，要解决问题(1)，产生一个随机标准化列的初始字典D0，通过固定字典不变而产生稀疏矩阵X。也就是找出每个训练信号yi对应于当前字典D的稀疏表示xi。所选择的稀疏编码算法必须限制非零元素的最大数量的解决方案，因此通常使用OMP算法[6]来得到稀疏表示矩阵X。

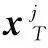
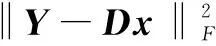
(2)

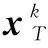
(3)

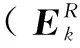
1.2 SBDL算法

SBDL算法是以最大后验概率为基础的算法，被用于稀疏基恢复。稀疏贝叶斯模型是通过一种特定的先验参数来优选稀疏系数组合的贝叶斯处理过程。基于高斯似然模型[7]的稀疏贝叶斯字典学习方式表示为：

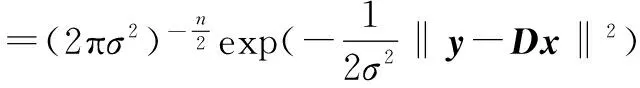
(4)

目标是最大化方程(4)中的向量x和常量σ2的似然估计。为了避免模型中与训练样本数量相等的参数数量造成严重的匹配问题，添加一个满足先验概率分布的参数，得到的满足零均值高斯分布的向量x的先验分布为：

(5)

其中，α=(α0,α1,…,αK)是一个由K个超参数组成的向量。

假设噪声参数σ2和超参数向量α满足Gamma先验概率分布，可以得到方程(6)中向量x的后验概率：

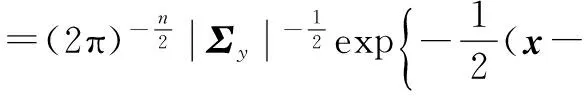
(6)

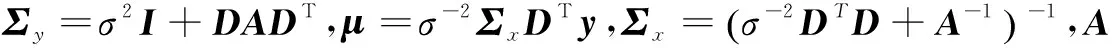
(7)

2 广义贝叶斯字典学习K-SVD算法(GBDL K-SVD)

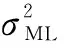
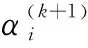
(8)

相似地，对于σ2的更新规则可以被如方程(9)简单地合成表示为：

(9)

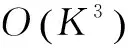
(10)

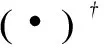
因此明显知道x所对应的α的稀疏概况和观察到所有的x都是可行的，并且如果y是D的跨度且所有的α被初始化为非零值，这将永远是可行的。

那么，GBDLK-SVD算法关键步骤如下所述：

步骤2(初始化)：过完备字典矩阵D(0)∈Rn×K，先验估计噪声方差σ2，超参数向量α=(α0,α1,…,αK)，并设置J=0和S=0。

步骤3(主程序)：执行J=J+1，重复如下步骤直到满足收敛或停止准则J≥Jmax：

1)执行S=S+1，重复如下步骤直到满足停止准则S≥Smax：

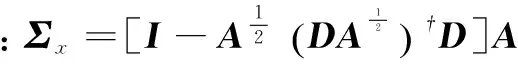
(3)更新噪声方差和超参数：

2)如果‖xi‖>T0，继续用OMP算法来优化向量x，直到满足‖xi‖≤T0。

3)更新字典，更新D(J-1)中k=1,2,…,K的每一列。

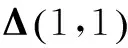
3 实验仿真和分析

3.1 字典学习结果对比分析

文中仿真实验使用由一组图像帧组成的视频序列作为样本，从由51个Y帧组成的视频信号中提取出大小为176×144的一组图像帧[10]。为提高视频图像帧的稀疏度，采用重叠块滑动窗口的块算法来获得分块图像。从图像帧获得多个8×8大小的重叠块，并将每个依次重新排列成维数是64的向量，最后以这些向量为列构成64×23 153大小的矩阵。选择过完备字典的大小为64×256，设定SBDL算法和GBDL算法的Smax=10,Jmax=10。经过视频序列分解和分块图像处理后，分别用SBDLK-SVD算法和GBDLK-SVD算法对图像帧进行稀疏编码，获得的基于图像块训练字典的结果如图1所示。

从图1可以看到，通过仿真实验，由SBDLK-SVD稀疏编码训练后的块信号，虽然训练信号的每一块的特点大致能够表现出来，但图像帧的训练特征不明显。然而，通过GBDLK-SVD算法稀疏编码后，被训练的标准信号的特征纹理较前一种字典训练后的特征更加突出，纹理更加清晰。因此，使用GBDLK-SVD过完备字典训练图像帧信号更具有前瞻性和有效性。

图1 算法训练结果

3.2 稀疏表示信号的重构性能对比分析

根据实际经验，视频经过媒介传输，在解码器端解码后会产生不同程度的失真。为了使仿真实验符合实际情况，随机地从视频序列中选择一个图像帧。首先，从图像帧中损失不同数量的像素，而后分别在SBDLK-SVD算法和GBDLK-SVD算法这两种过完备稀疏字典学习算法的训练下，重构出非损失像素的图像帧。为直观地比较不同学习字典的效果，对损失像素范围在10%～90%的图像帧进行重构，得到的对比结果如图2所示。

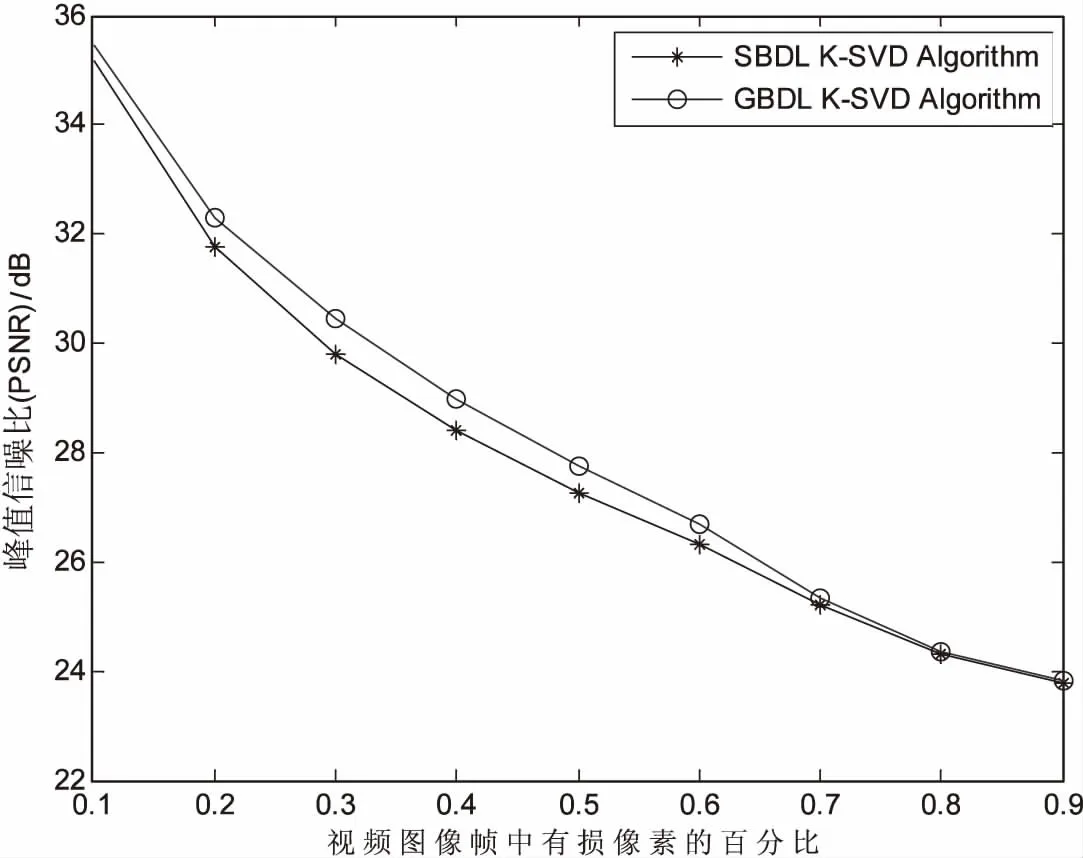
图2 过完备稀疏字典对不同程度有损

从图2可以看到：若图像帧有损像素比例是10%，经两种不同稀疏字典稀疏表示后重构出的图像帧的峰值信噪比(PSNR)可以上升到35dB左右。损失的像素占原像素的比率越低，过完备字典稀疏表示后的重构图像的PSNR值都相对较高。但随着损失像素的比例相对增加，获得的PSNR值近似线性下降。通过GBDLK-SVD算法获得的PSNR值总是高于SBDLK-SVD算法获得的PSNR值。因此改进后的过完备字典学习算法比原始的稀疏表示性能强，这是由于改进算法稀疏编码步骤中新更新模式考虑了EM算法最大化后验概率。因此通过GBDLK-SVD算法获得的信号稀疏表示来处理损失像素的图像帧具有更好的性能。

压缩感知[11-12]是近年来新兴的技术并逐渐成熟，它主要包含信号的采样稀疏、压缩测量和重构三个主要步骤。采样稀疏也就是常说的稀疏编码，它在压缩感知技术中起着举足轻重的作用。在稀疏编码步骤中，选择一个合适的稀疏变换基或矩阵Ψ，或者选择一种过完备字典稀疏学习来获得信号的稀疏表示系数，再通过对稀疏系数的压缩测量，获得一个低维的向量。信号通过传输媒介后，在解码器端获得压缩后的信号。为了获得原始信号的逼近值并重构出图像帧，通常情况下采用贪婪迭代算法重建图像帧，如：正交匹配追踪(OMP)[8]、分段正交匹配追踪(StOMP)[13]和稀疏度自适应匹配追踪(SAMP)[14]。

为了比较稀疏表示算法的性能，设置了从0.3到0.7范围的不同采样率，对比结果见图3。其中，m表示图像矩阵列向量的维数，采样率表示获得的信号数量占原始图像帧数量的比率。

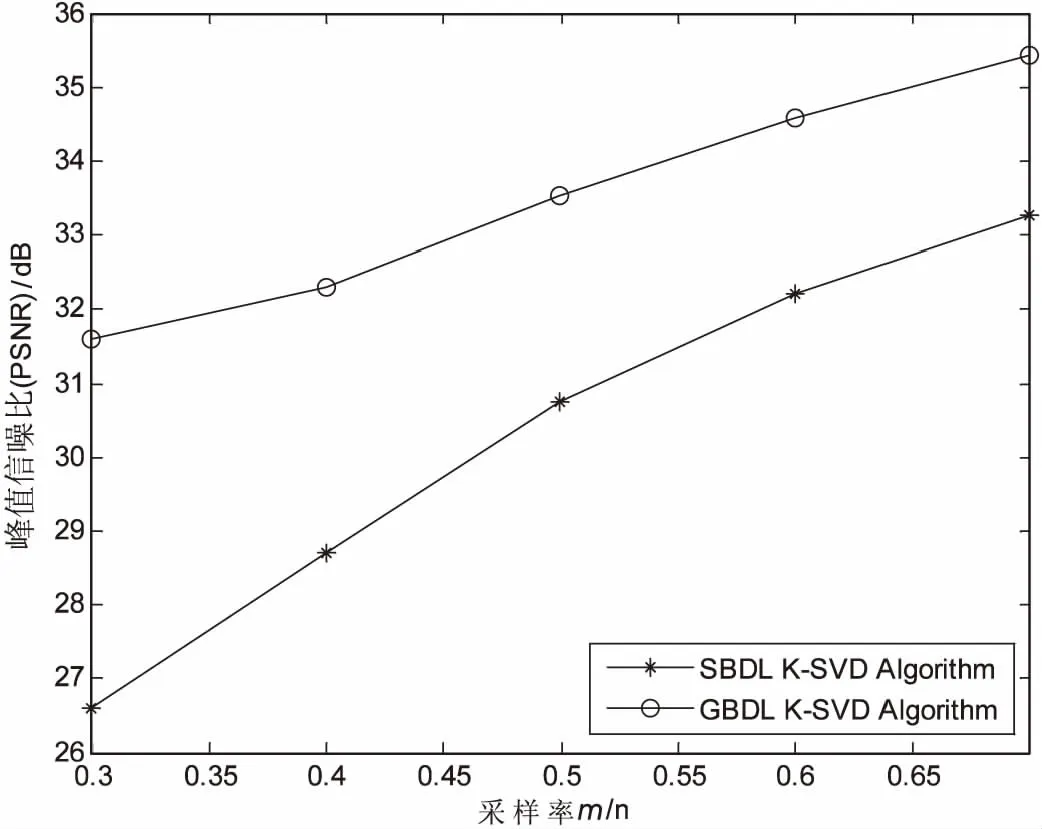
图3 过完备稀疏字典对基于压缩感知

从图3可以看出，当采样率较低时，经两种算法稀疏表示后的重构图像帧的PSNR值相对较低，但随着采样率增加，PSNR值也明显提高。通过GBDLK-SVD算法获得的PSNR总是高于SBDLK-SVD算法获得的PSNR。

所以改进后的算法具有更强的重构性能，这很大程度上取决于它的稀疏表示系数在新型更新模式中使得学习算法逐渐收敛。

4 结束语

文中通过深入研究过完备稀疏字典学习的稀疏表示方法，提出了GBDLK-SVD算法。对稀疏编码步骤做出改进，改进协方差矩阵的计算和稀疏向量的估计方式，进而改进了常量σ2和γ的更新模式，提高了重构精度，加快了收敛速度。此外，仿真实验表明，在有损像素的图像帧和基于压缩传感的图像帧两种情况下，视频图像帧通过GBDLK-SVD算法稀疏表示后的重构效率高于SBDLK-SVD稀疏字典学习算法。总而言之，改进的过完备字典学习始于非稀疏表示信号，并通过迭代过程逐步收敛到一个稀疏表示系数。实验结果说明了提出算法的正确性并证实了其有效性。

[1]DelgadoKK,MurrayJF,RaoBD.Dictionarylearningalgorithmsforsparserepresentation[J].NeuralComputation,2003,15(2):349-396.

[2]MairalJ,BachF,PonceJ,etal.Onlinelearningformatrixfactorizationandsparsecoding[J].JournalofMachineLearningResearch,2010,11:19-60.

[3]SongXN,LiuL,YangXB,etal.AparameterizedfuzzyadaptiveK-SVDapproachforthemulti-classesstudyofpursuitalgorithms[J].Neurocomputing,2014,123:131-139.

[4]AharonM,EladM,BrucksteinA.K-SVD:analgorithmfordesigningovercompletedictionariesforsparserepresentation[J].IEEETransactionsonSignalProcessing,2006,54(11):4311-4322.

[5]TroppJA,WrightSJ.Computationalmethodsforsparsesolutionoflinearinverseproblems[J].ProceedingsoftheIEEE,2010,98(6):948-958.

[6]TroppJA,GilbertAG.Signalrecoveryfrompartialinformationviaorthogonalmatchingpursuit[J].IEEETransactionsonInformationTheory,2007,53(12):4655-4666.

[7]BabacanSD,MolinaR,KatsaggelosAK.Bayesiancompressivesensingusinglaplacepriors[J].IEEETransactionsonImageProcessing,2010,19(1):53-63.

[8]ZhouFF,LiL.ModifiedsparseBayesiandictionarylearningK-SVDalgorithmforvideoimagesparserepresentation[J].JournalofComputationalInformationSystems,2015,11(12):4567-4580.

[9]WipfDP,RaoBD.SparseBayesianlearningforbasisselection[J].IEEETransactionsonSignalProcessing,2004,52(8):2153-2164.

[10]SunYP,XuM,TaoXM,etal.Onlinedictionarylearningbasedintra-framevideocoding[J].WirelessPersonalCommunications,2014,74:1281-1295.

[11]DonohoDL.Compressedsensing[J].IEEETransactionsonInformationTheory,2006,52(5):1289-1306.

[12]ZhouFF,LiL.ResearchonclippingthresholdSAMPalgorithmbasedonhighfrequencysub-bandwavelettransform[J].ComputerTechnologyandDevelopment,2014,24(5):83-86.

[13]DonohoDL,TsaigY,DroriI.Sparsesolutionofunderdeterminedsystemsoflinearequationsbystagewiseorthogonalmatchingpursuit[J].IEEETransactionsonInformationTheory,2012,58(2):1094-1121.

[14]ThongT,GanL,NguyenN,etal.Sparsityadaptivematchingpursuitalgorithmforpracticalcompressedsensing[C]//ProcofAsilomarconferenceonsignal,systemsandcomputers.PacificGrove,California:[s.n.],2008.

K-SVD Sparse Representation Algorithm of Generalized Bayesian Dictionary Learning

ZHOU Fei-fei，LI Lei

(College of Science，Nanjing University of Posts and Telecommunications，Nanjing 210023，China)

Sparse dictionary learning is a powerful sparse representation method for video image which has attracted much attention in exploiting sparsity in signal processing.The K-SVD algorithm has achieved success in sparse representation but suffers from the problem of underutilization of dictionary atoms.Sparse Bayesian Dictionary Learning (SBDL) algorithm exists the drawbacks of non-sparse representation and convergence of signal atoms.But Generalized Bayesian Dictionary Learning (GBDL) K-SVD algorithm offers a novel update mode of sparse represent coefficient to make the learning algorithm gradually convergent and give the training vectors a perfect opportunity to become extremely sparsity over the overcomplete dictionary.The simulation experiment of two cases where image frames with missing pixels and ones based on compressive sensing shows that the efficiency of sparsely represent by GBDL K-SVD algorithm is better than SBDL K-SVD algorithm.

sparse Bayesian learning;video image sparse representation;dictionary learning;K-SVD algorithm

2015-07-25

2015-11-05

时间：2016-05-05

国家自然科学基金资助项目(61071167,61373137)；江苏省研究生科研创新计划项目(KYZZ_0233)

周飞飞(1990-)，女，硕士研究生，研究方向为非线性分析及应用；李 雷，博士，教授，研究方向为智能信号处理和非线性科学及其在通信中的应用。

http://www.cnki.net/kcms/detail/61.1450.TP.20160505.0817.050.html

TP301.6

A

1673-629X(2016)05-0071-05

10.3969/j.issn.1673-629X.2016.05.015