基于RSSI滤波的改进型泰勒级数室内定位算法

程 俊，周礼争，余 敏，唐 瑞

(1.江西师范大学 计算机信息工程学院，江西 南昌 330022；2.江西师范大学 软件学院，江西 南昌 330022)

基于RSSI滤波的改进型泰勒级数室内定位算法

程 俊1，周礼争1，余 敏1，唐 瑞2

(1.江西师范大学 计算机信息工程学院，江西 南昌 330022；2.江西师范大学 软件学院，江西 南昌 330022)

针对基于RSSI测距的无线传感网络室内定位算法中，RSSI值易受环境影响、定位精度差的问题，文中提出了一种RSSI值优化处理、泰勒级数进行改进的定位算法。该算法先将采集的RSSI值进行高斯-卡尔曼滤波处理，然后在不用求模型参数的情况下，引入降维思想求出了测距值，最后对泰勒级数进行改进，并用加权极大似然和改进的泰勒级数相结合的定位算法求出了定位位置。仿真结果表明：经过RSSI滤波的改进型泰勒级数定位算法，优化了RSSI值，提高了测距精度，使得定位算法的定位误差维持在0.9～1.2 m，提高了定位的稳定性和精确度。

接收信号强度指示；室内定位；高斯-卡尔曼滤波；模型参数；泰勒级数

0 引 言

近年来，随着无线传感器网络(Wireless Sensor Network，WSN)[1]的快速发展，无线定位技术的应用进入了一个崭新的时代。在各种体育馆、复杂的购物商场等大型建筑，为了获得人员或物品的确切位置，室内定位技术显得格外重要。目前，无线传感器网络的室内定位技术可以分为测距和非测距两大类[2-3]。测距算法包括TOA[4]、TDOA[5]、RSSI[6]、AOA[7]等；非测距算法包括APIT[8]、凸规划法、质心法、DV-Hop[9]等等。

基于RSSI测距的室内定位算法操作简单，无需额外大量硬件，使之得到了广泛应用[10]。但是由于RSSI值易受环境影响，所以此方法得到的定位结果会存在很大误差[11]。文献[12]用高斯滤波减少了RSSI样本中偏离真实值较大的部分，使得滤波得到的RSSI值更加准确。文献[13]提出了一种基于RSSI距离比的定位算法，在测距阶段利用距离比关系消除了模型参数A，减少了因为计算模型参数带来的误差，提高了测距精度。文献[14]将加权极大似然法得到的值，作为泰勒级数的初始展开位置，有效减少了泰勒级数迭代的次数，降低了定位误差。

受上述相关研究的启发，文中提出了基于RSSI高斯-卡尔曼滤波的改进泰勒级数和加权极大似然法相结合的定位算法。

1 RSSI值的优化

1.1 传统滤波方法分析

室内定位中，由于存在人员走动、信号反射等不稳定因素，使接收的RSSI值存在很大误差。为了提高其精确度，常常对其进行滤波处理，其中高斯滤波、卡尔曼滤波是常用的滤波处理方法。高斯滤波可以解决RSSI在实际测试中易受干扰、稳定性差等问题，但对于阴影效应、电子仪器本身干扰等长时间干扰问题处理效果欠佳，无法对数据进行平滑输出；卡尔曼滤波能去除叠加在信号上的加性噪声，平滑显著误差，但却无法去除误差，若末尾几个测量值误差大，将对结果产生重大影响。

1.2 高斯-卡尔曼滤波优化RSSI值

文中采用混合滤波的方法，将卡尔曼滤波、高斯滤波相结合，提出高斯-卡尔曼滤波。该滤波先对采集的RSSI值信号进行高斯拟合，筛选出高概率发生区域的RSSI值，再对筛选出的RSSI值进行卡尔曼滤波。

1.2.1 高斯滤波取值

同一个节点接收到的多个RSSI值，由于各种干扰，必然存在由误差引起的小概率事件，通过高斯模型可以筛选出高概率发生区的RSSI值。

设RSSI服从(0,δ2)的高斯分布，其概率密度函数为：

(1)

1.2.2 卡尔曼滤波

高斯滤波取值可以滤除一大部分偏离真实值的RSSI值，但是对于叠加在信号上的加性噪声，则无能为力。而且传统的高斯滤波只是对高斯滤波取值后的数据进行简单的求平均，并不能平滑RSSI值，为此文中在高斯滤波取值后进行了卡尔曼滤波。其具体过程如下：

状态预测方程为：

(2)

状态更新方程为：

(3)

式中：X(k|k-1)为目前状态的预测值，X(k-1|k-1)为上一转态值；A、B为系统参数；U(k)为现在转态的控制量，如果没有，可以为0；P(k|k-1)为对应于X(k|k-1)的协方差，P(k-1|k-1)为X(k-1|k-1)对应的协方差；Q为系统噪声；Z(k)为k时刻的测量值；H为测量系统的参数；Kg(k)为卡尔曼滤波增益；R为量测噪声；P(k|k)为目前转态的更新值；I为单位矩阵，对于单模型单测量，I=1。

由式(2)和(3)可以看出，卡尔曼滤波可以通过“预测-更新”的模型递归思想，由系统的实际测量值和预估值来消除随机噪声，用上一状态RSSI预估值和现在状态RSSI的测量值来推导出现在现在状态的RSSI值，平滑了数据。

综上所述，通过高斯-卡尔曼滤波，可以有效去除RSSI数据中的突变数据和噪声波动，实现RSSI值的准确、平滑输出，为测距模型的精确建立打下基础。

2 无需测量模型参数的测距算法

假设定位节点周围有n个锚节点单播互发空侦，它们之间一跳的距离为r1,r2,…,rn，相对应的经过高斯-卡尔曼滤波的RSSI值为|RSSI1|,|RSSI1|,…,|RSSIn|，则根据对数模型可得：

(4)

公式可以写成Y=bX形式，其中：

(5)

由于A和n计算繁琐，而且如果算法不合理或考虑不全面，将会影响到后面的定位算法。为此，引入了降维的思想，在Y=bX两边同时左乘bT，将矩阵降至2维，得公式如下：

(6)

(7)

通过式(6)和(7)可以将bTY=bTbX还原为二元二次方程，再结合未知节点的距离信号关系方程，可列出以下方程组：

(8)

(9)

3 定位算法的改进

3.1 加权极大似然和泰勒级数结合的定位算法

Taylor级数展开定位法具有很高的定位精度，但是倘若初值设置不当，将使迭代次数增加，计算复杂度大大增加。文献[9]将加权似然法得到的初始坐标作为泰勒级数的初始展开位置，减少了迭代次数，降低了定位误差，其具体步骤如下：

(10)

真实坐标可表示为加权似然得到的坐标与位置偏移量之和：

x=x′+Δx,y=y′+Δy

(11)

在节点估计坐标(加权似然法得到的坐标)处按泰勒级数展开(消除非线性项)：

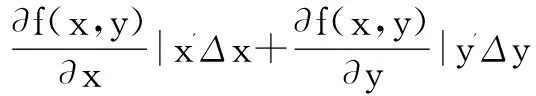
(12)

将式(12)用矩阵表示：

B=AΔ

(13)

其中：

方程的解为：

Δ=(ATA)-1ATB

(14)

令：

重复上述过程，直到|Δx|+|Δy|<ε，ε为预先设定的阈值，将此时的(x',y')作为定位节点的最终估计位置。

3.2 加权极大似然和改进型泰勒级数结合的定位算法

根据这一思想，可以对泰勒级数做如下改进：

QB=AΔ

(15)

(16)

最后，用加权极大似然法计算出初始估计坐标，代入改进的泰勒级数展开，可以得到新的定位结果。

4 实验结果与分析

文中采用Matlab对提出的算法进行仿真实验，以此来验证算法的有效性。仿真环境设计在一个8 m×6 m的矩形区域，用障碍物无规则的移动(快速、中速、慢速都有可能)代替室内环境下的人员走动，并在区域中加入均值为0、方差为4dB的高斯白噪声。然后在同一高度的四个角落布置4个锚节点，其坐标分为(0,0),(8,0),(0,6),(8,6)，锚节点和未知节点的采样频率都为5 次/s，同一段连续时间后，未知节点采集到不同锚节点发送的200次RSSI信号，每个锚节点采集到其他不同锚节点发送的200次RSSI信号，然后改变未知节点位置，重复上述实验10次，获得10组不同的数据。

4．1 滤波性能的分析

每一次实验都分别从4个锚节点发送给未知节点的200次RSSI信号中随机取出50个值，将它们重新整合，建立样本，并以样本标准差σs作为滤波性能的判定，其公式为：

(17)

其中：RSSI为样本平均值；RSSIi为采样点上滤波值。

图1比较了高斯滤波、卡尔曼滤波、高斯-卡尔曼滤波对RSSI的滤波性能。

图1 RSSI样本标准差对比图

由图1可以发现：

(1)卡尔曼滤波模型的RSSI样本标准差波动比较大。这是由于，当显著误差不多时，卡尔曼滤波能在一定程度上将采样值平滑输出，而当显著误差较多时，由于卡尔曼滤波只能平滑显著误差，无法去除，其去除显著误差的能力不如高斯模型。

(2)高斯滤波能够消除显著误差，并在一定程度上减小由于短时间干扰引起的RSSI值波动比较大的情况，使得σs偏差维持在1.5dBm左右。

(3)经过高斯-卡尔曼滤波后，RSSI样本标准差误差维持在1dBm左右，相比高斯模型，其整体上波动更小，滤波性能更稳定，平滑了RSSI的输出值。

4．2 定位精度的分析

将未知节点和锚节点收到的200次RSSI信号进行高斯-卡尔曼滤波，并通过式(9)求得未知节点到锚节点的距离，最后进行定位实验。

选取定位误差e作为定位性能的判定，其公式为：

(18)

其中，未知节点真实坐标为(x0,y0)，计算得到的坐标为(x,y)。

图2比较了两种定位算法：加权极大似然和泰勒级数结合的定位算法、加权极大似然和改进泰勒级数结合的定位算法。

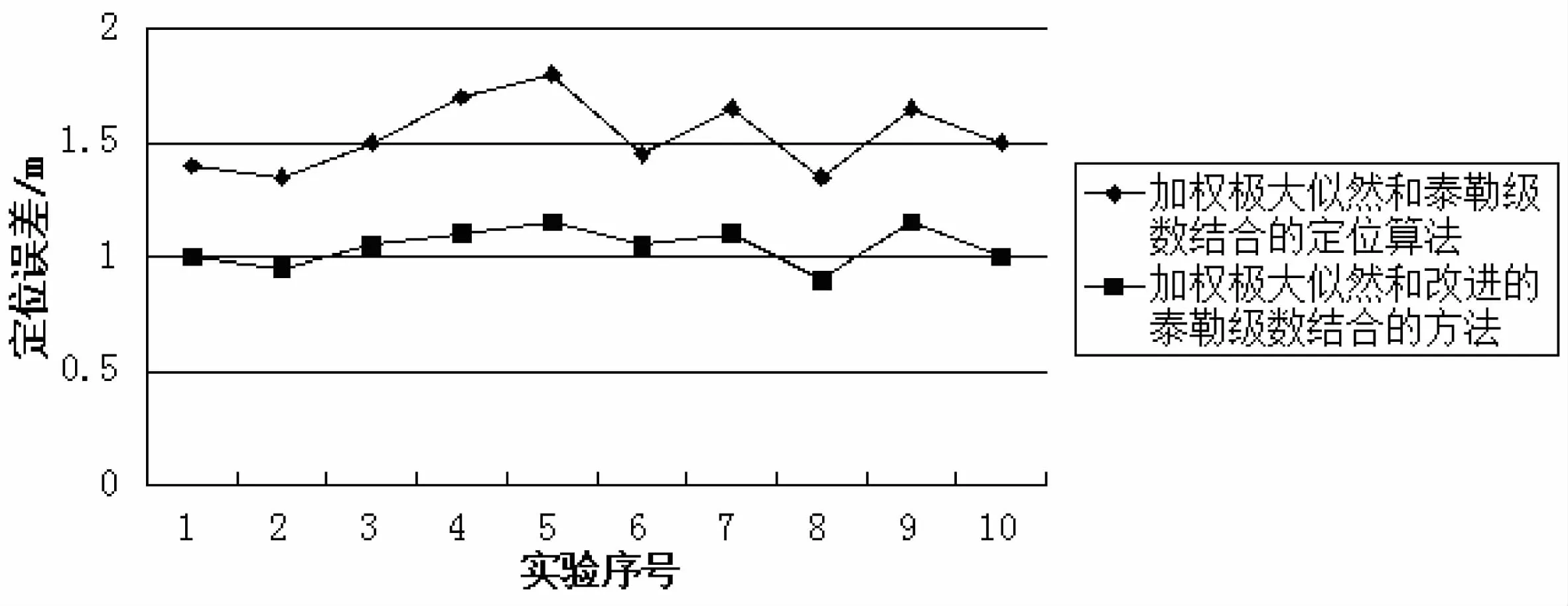
图2 定位误差对比图

由图2可知：

(1)和传统定位方法相比，改进的方法整体上的定位误差明显小于传统方法。传统定位方法的定位误差为1.5m左右，而改进的方法降低为1.0m左右。

(2)传统定位方法的定位误差波动范围为1.2～1.8m，而改进的定位算法由于考虑了距离因素的影响，定位误差波动范围减小为0.9～1.2m，减少了定位误差，提高了定位的稳定性。

5 结束语

文中针对室内环境下基于RSSI测距的定位算法误差比较大的问题，提出先用高斯-卡尔曼滤波优化RSSI值，然后利用锚节点的关系，在不用测模型参数的情况下，求出了测距值，最后对泰勒级数进行改进，并将加权极大似然法和改进的泰勒级数相结合求出了定位位置。实验结果表明：基于高斯-卡尔曼滤波的加权极大似然和改进泰勒级数相结合的定位算法，有效减少了定位误差，使得定位误差维持在0.9～1.2m，提高了定位的准确度和稳定性。

基于高斯-卡尔曼滤波的加权极大似然和改进泰勒级数相结合的定位算法提高了定位精度，但仍存在一定的局限，以后可以从以下几个方向进行改进：

(1)加权极大似然和改进泰勒级数相结合的定位算法，增加了算法复杂性。下一步工作将寻找某种算法，使得定位精度提高的同时，减小算法的复杂度。

(2)文中针对的只是基于RSSI测距的静态定位算法，下一步将考虑在未知节点移动的情况下，如何进行有效定位的问题。

[1]YickJ,MukherjeeB,GhosalD.Wirelesssensornetworksurvey[J].ComputerNetworks,2008,52(12):2292-2330.

[2]NasipuriA,LiK.Adirectionalitybasedlocationdiscoveryschemeforwirelesssensornetworks[C]//ProceedingsofACMinternationalworkshoponwirelesssensornetworksandapplication.Atlanta,USA:ACM,2002:105-111.

[3] 彭 渤.基于RSSI测距误差补偿的无线传感器网络定位算法研究[D].大连:大连理工大学,2008.

[4]HanerA,HopperA,StegglesP,etal.Theanatomyofacontext-awareapplication[C]//Procofthe5thannualACM/IEEEinternationalconferenceonmobilecomputingandnetworking.[s.l.]:ACM,1999.

[5] 陈鸿龙,李鸿斌,王 智.基于TDOA测距的传感器网络安全定位研究[J].通信学报,2008,29(8):11-21.

[6]LuthyKA,EgrantD,HendersonTC.LeveragingRSSIforroboticrepairofdisconnectedwirelesssensornetworks[C]//Procof2007IEEEinternationalconferenceonroboticsandautomation.[s.l.]:IEEE,2007:10-14.

[7]ZengFanzhen，YuMin，ZouChengwu,etal．Animprovedpointintriangulationlocalizationalgorithmbasedoncosinetheorem[C]//Procof2012 8thinternationalconferenceonwirelesscommunications,networkingandmobilecomputing.Shanghai,China:IEEE,2012:1652-1655．

[8]ZhangJianping,YuMin,ZhangKe,etal.AnimprovedweightedtrianglecentroidlocalizationalgorithmofAPITforwirelesssensornetworks[C]//Procof2012internationalconferenceoncomputerandinformationscience,safetyengineering.Wuhan,China:IEEE,2012:18-21.

[9]ZhangDengyin,CuiGuodong.AnunionnodelocalizationalgorithmbasedonRSSIandDV-HopforWSNs[C]//Procof2012secondinternationalconferenceonIMCC.[s.l.]:[s.n.],2012:1094-1098.

[10] 陶为戈,朱昳华,贾子彦.基于RSSI混合滤波和最小二乘参数估计的测距算法[J].传感技术学报，2012,25(12):1748-1753．

[11] 吴君钦,卢 陶.基于RSSI测距的无线传感器网络定位算法[J].微电子学与计算机，2014,31(5):49-52.

[12] 董莹莹.WiFi网络下的三维空间定位技术研究[D].北京:北京邮电大学,2012.

[13] 吴桂平,虞慧群,范贵生.一种基于RSSI距离比的传感器节点定位算法[J].华东理工大学学报:自然科学版,2013,39(5):596-600.

[14] 肖婷婷.基于RSSI测距的室内定位算法研究及改进[D].南昌:江西师范大学,2015.

Indoor Localization Algorithm of Improved Taylor Series Based on RSSI Filter

CHENG Jun1,ZHOU Li-zheng1,YU Min1,TANG Rui2

(1.School of Computer Information and Engineering,Jiangxi Normal University,Nanchang 330022,China;2.School of Software,Jiangxi Normal University,Nanchang 330022,China)

Aiming at the problem that the RSSI is susceptible to the environment and the accuracy is poor in the indoor localization of wireless sensor networks,a kind of positioning algorithm is proposed by the optimized RSSI and the improved Taylor series.Firstly,all measured RSSI that the node received are processed by the Gauss-Kalman filtering.Although it does not introduce the model parameters,the value of ranging is got by thought of dimension reduction.Finally,the Taylor series is improved and the position is got by the weighted maximum likelihood estimation method and the improved Taylor series.The simulation shows that the RSSI is optimized and the accuracy of ranging is improved by the indoor localization algorithm of the improved Taylor series based on RSSI filter.It made the accuracy kept between 0.9 to 1.2 m,improving the accuracy and stability of the indoor positioning.

received signal strength indication;indoor localization;Gauss-Kalman filter;model parameters;Taylor series

2015-08-11

2015-11-12

时间：2016-05-05

国家自然科学基金资助项目(41374039)；国际科技合作项目(35-14)

程 俊(1989-)，男，硕士研究生，研究方向为无线传感网络；余 敏，教授，硕士生导师，研究方向为无线传感网络。

http://www.cnki.net/kcms/detail/61.1450.TP.20160505.0828.072.html

TP393

A

1673-629X(2016)05-00051-05

10.3969/j.issn.1673-629X.2016.05.011