基于SEIRS模型的机场飞行区人为风险传染过程研究
唐辛欣, 罗 帆
(武汉理工大学 管理学院,湖北 武汉 430070)
基于SEIRS模型的机场飞行区人为风险传染过程研究
唐辛欣, 罗 帆
(武汉理工大学 管理学院,湖北 武汉 430070)
为更科学合理地结合风险演化规律和传染过程进行风险管控,构建了基于SEIRS(susceptible-exposed-infected-recovered-susceptible,易感群体-潜伏群体-感染群体-免疫群体-易感群体)传染病模型的机场飞行区人为风险传染过程模型,界定了模型的假设条件,并分析了模型的平衡点及稳定性,模型在平衡点均为渐进稳定的。运用Matlab对模型进行模拟仿真,风险传染初期、中期和末期潜伏群体、感染群体和免疫群体最终均趋于零平衡。其中潜伏群体呈较为平滑的递减趋势,感染群体在急速减少后逐渐趋于零平衡,免疫群体均短期内快速增长后迅速回落。不同阶段各群体的变化率有显著区别。末期潜伏群体在急速减少后呈缓慢上升趋势,最终趋于零平衡。结论为风险管控不同阶段的策略重点提供了理论依据。
人为风险; 风险传染; 机场飞行区; 传染病模型
近年来,随着航空工作人员工作量和工作压力的增加,因人员操作失误或人员心理问题等人为风险酿成的航空灾难不断增多。如2015年复兴航空客机坠落、2014年韩亚航空坠机、中华航空1994年和1998年接连发生两次飞机坠毁等国内外多起重大航空事故,皆因飞行员人为操作失误、与空中交通管制员沟通障碍等人为责任所导致。高危性、生还率低等特点使得频发的航空事故给国民安全和财产造成了严重损失,航空安全风险管理工作也受到了严峻的挑战。飞行区作为机场的重要组成部分,与航空器安全联系最为紧密,其安全保障能力直接影响着旅客和航空器的安全。机场飞行区人因差错最终造成人员风险,演化为设备设施风险、环境风险和管理风险等其他表现形式的风险。这些风险为机场飞行区安全埋下隐患,对航空安全的威胁也不断增大。对机场飞行区人为风险传染过程的研究,能更好地总结风险演化的规律,对风险实行分类、分阶段针对性管控,并根据研究结论归纳切实有效的风险管控措施,以保障机场飞行区安全。
机场飞行区是指为飞机地面活动及停放提供适应飞机特性要求和保证运行安全的构筑物的统称,包括跑道、升降带、滑行道、停机坪、地面标志、灯光助航设施及排水系统。其中机坪、跑道和净空等对机场安全威胁最大。飞行区所涉及到的工作人员包括飞行区管理部行政人员及一线员工、空中交通管制员、飞行员、车辆驾驶员,行人等,其在工作中的失误都可能危及机场安全。本文将机场飞行区人为风险界定为:在机场飞行区范围内,由人为责任所带来的不安全事件发生的风险,其中不安全事件包括安全事故、事故征候和其他不安全事件等。如飞机滑出跑道可能涉及飞行员操作失误、情境丧失、与管制员通讯沟通障碍、视线受阻等人为责任,将这类风险定义为人为风险。人因所导致的可能诱发不安全事件的隐患和风险,其风险的传染兼具风险演化及生物传染系统,如人员情绪、行为传染的特征。
生物传染系统的运作表现为病原体经传播途径,从传染源感染到易感人群,出现病征的易感人群转为患者;携带病原体,但是并没有出现明显病征的转为携带者;通过病原体入侵获得免疫能力的易感人群转为免疫者。有别于医学上的传染的概念,风险管理中的传染主要是指通过语言或行动引起他人相同的思路感情和行为。风险传染是指正面或负面影响的不确定性在不同主体之间的传染过程,是由存在风险的主体向其他主体传递风险的过程。构成传染的过程需要3个条件:病原体的致病性、机体的反应性和外界环境的影响。传染病模型主要为传染能力相同模型,包括SIRS(susceptible-infected-recovered-susceptible,易感群体-感染群体-免疫群体-易感群体)模型、SEIRS模型(susceptible-exposed-infected-recovered-susceptible,易感群体-潜伏群体-感染群体-免疫群体-易感群体)和SIRSLS(susceptible-infected-recovered-susceptible model with lower susceptibility,低易感性的易感群体-感染群体-免疫群体-易感群体模型)等[1]。机场飞行区人为风险的演化也是从一个风险源向另一个风险源感染的过程,风险源在受到感染时也呈现出不同的状态和结果。
国内外对于风险传染的研究主要集中在经济金融方面,从系统的角度出发,运用复杂网络[1-2]、动态性和时间序列相结合[3-6]、蒙特卡洛模型[7]、KMV模型、DCC-MSV模型[8]等分析工具和方法探究风险传染的机理[9],构建了危机的传染病动力学模型[10-12],以检验系统的某一特定时期的风险传染难易程度[9]、系统动态的脆弱性的相关度等[7],通过境外关联,对风险传染的规避具有一定的积极作用[1-2]。且风险的传染还具有一定的方向性[13-14],存在羊群效应[15-16]和依赖结构[17]。在航空风险演化和传递方面,运用复杂网络理论[18-19]、动力学模型[20-21]等对航空风险的演化规律、途径和模式进行了深入探究。在SEIRS模型应用方面,学者基于研究对象的恐慌源、阶段性、流行性和免疫性,将SEIRS模型应用于员工离职恐慌行为的传染[22]、食品行业突发事件风险感知[23]、商业模式扩散机制[24]等方面的研究。此外,有国内外学者就突发事件中群体的行为和情绪的传播机理进行了探究,运用前景理论[25]、分对数离散选择模型[26]、SI(susceptible-infected,易感群体-感染群体)传播模型[27]、演化博弈论方法[28]等对交通、舆情等方面风险决策和传播的群体行为的规律进行了研究。
综上所述,国内外学者对于传染机理的研究已经逐渐从医学领域逐渐延伸到其他领域,包括风险管理领域等。而在风险管理领域中传染机理的研究,则更多集中在金融方向。近年来,随着工作人员心理问题的突出,国内外学者开始将研究目光转到如员工离职风险、员工行为风险等方面。由于机场人为风险传播和演化途径与群体行为和情绪的传播、演化途径相似,因此可借鉴传染病或大众传播模型进行人员风险演化的研究,运用复杂网络[29]、动力学模型等进行风险传染的仿真模拟。通过国内外文献的查阅,为人为风险传染机理的研究提供了较多思路和视角。
1 模型构建
1.1 方法适用性论证
机场飞行区人为风险的演化和防范具有生物传染和免疫系统共同的特征:可追溯性、阶段性、传染性和免疫性。在实际生物体传染研究中,很难采取试验的形式获取数据,历史资料不完全、不充分。且不同类型的传染病传播过程特点不同,较难从纯医学的角度进行传染的分析。因此,在探究传染系统的传染机理时,按照大众传播机理建立模型,并结合生物传染系统的特点,进行模型的修正和优化,构建传染病模型。运用较为成熟的传染病模型进行机场飞行区人为风险传染过程的研究,符合机场飞行区人为风险特性和演化规律,能更好地梳理和探究风险构成要素和内在变化规律。
传染病模型是由常微分方程所描述的用以刻画传染病传播和流行规律的建模方法。目前普遍采用的传染病模型主要有:SI模型、SIS(susceptible-infected-susceptible,易感群体-感染群体-易感群体)模型、SIR(susceptible-infected-recovered,易感群体-感染群体-免疫群体)模型等。通过各类模型对比可见,SI模型虽不适用于机场飞行区人为风险传染的研究,但其对于所涉及主体的分类和主体行为的研究仍有一定的启示意义;SIR模型虽考虑了免疫者的存在,但并未考虑免疫者获得免疫能力后可能会由于环境的变化、自身抵抗能力等影响丧失免疫能力,再次成为具有传染性的群体进入到传染系统中的情况。机场飞行区人为风险的日常管控中,将由于风险暴露采取管控措施较好地规避的风险类比为免疫群体,但这种风险规避是有一定时效性的,在一定时间段后,已规避风险会再次以传染源进入风险的传染系统中。SIS模型考虑到免疫者可能由于疾病特征或群体自身免疫力的原因,在获得免疫能力后仍为易感群体,符合机场人为风险不能达到长期免疫效果的特性。而在机场人为风险的研究时期内,风险源增加或减少的情况较少,故出生率和死亡率可考虑不计。
由于风险发生前存在一定的潜伏期,且在未显现病症之前一直处于隐显状态,本文在SIR模型的基础上,建立SEIRS传染病模型,对机场飞行区人为风险传染过程和演化机理进行研究,且不考虑出生率和死亡率。
1.2 模型的假设条件
在模型构建之前,本文作出如下假设。
1)假设机场飞行区人为风险传染的周期较短,且在该周期内,参与作业的人员、设备等主体的数量是固定不变的,即排除员工及设备设施增加或减少的情况。
2)将机场飞行区人为风险分为易感群体、潜伏群体、感染群体和免疫群体4类,其中免疫群体具有一定免疫能力,但可能由于病原体变异、免疫能力丧失等原因仍存在被传染的可能,分别用S(t)、E(t)、I(t)和R(t)来表示t时刻4类群体在总的风险源中所占的比例,其中t>0,4者存在如下关系:
S(t)+E(t)+I(t)+R(t)=1。
(1)
3)β为染病的风险源的传染率,ε为潜伏群体因风险被传染病症显现而转化为感染群体的比例,γ为感染群体转化为免疫群体的比例,δ为免疫群体因免疫能力变弱而转化为易感群体的比例,其中,β、ε、γ和δ均为0~1之间的常数。
4)将1/ε、1/γ、1/δ分别定义为平均潜伏期、平均染病周期和平均免疫期。
1.3 模型的平衡点及稳定性分析
基于以上假设,根据动力学原理,建立如下机场飞行区人为风险传染病模型微分方程组:
(2)
对模型进行讨论,存在如下情况:
当δ=0,即1/δ→∞时,机场飞行区人为风险系统内免疫群体的免疫能力可持续,不会减弱,免疫群体不会被传染转化为易感群体,因此缺少免疫群体向易感群体转化的环节,模型简化为SEIR模型;
当δ→∞,即1/δ→0时,免疫群体可被忽略,模型中缺少免疫群体,简化为SEIS模型;
当ε→∞,即1/ε→0时,潜伏群体被忽略,模型中缺少潜伏群体,模型简化为SIRS模型。
对模型的平衡点进行讨论,包括风险规避的平衡点和风险流行的平衡点。
1)风险规避平衡点及稳定性。
在机场人为风险传染系统中,当潜伏群体、感染群体和免疫群体均为0,即系统内均为易感群体时,达到风险规避的平衡状态。此时,微分方程的取值为p0(1,0,0,0),系统在该点风险均得到有效规避,不存在风险传染的状态。但此状态为理想状态,实际中是不存在的。
对于微分方程组进行讨论,由于S(t)+E(t)+I(t)+R(t)=1,故讨论微分方程式,只需其中3个方程满足条件即可。运用雅克比(Jacobian)矩阵进行平衡点分析,uij是关于x1,x2,…,xn的m维方程组,x1,x2,x3分别表示潜伏群体、感染群体和免疫群体所占比例。则对于uij来说,其雅克比矩阵为
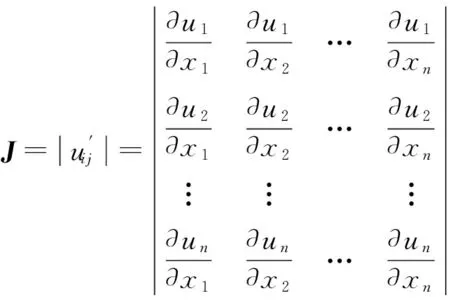
(3)
因此,平衡点p0处的雅克比矩阵为

(4)
求解该矩阵的特征方程为:(λ+δ)×(-1)3+3×[(λ+ε)(λ+γ)+βε]=(λ+δ)[λ2+(γ+ε)λ+(λ+β)ε]=0。可见,J0的一个特征根为λ1=-δ,而δ∈(0,1],则λ1>0。另外两个特征根由方程λ2+(γ+ε)λ+(λ+β)ε=0的解决定,有假设可得β、ε、γ和δ均为0~1之间的常数,则γ+ε>0,(λ+β)ε>0,两个特征根λ2、λ3为负实数或存在负实部。根据李雅普诺夫(Lyapunov)稳定性判别定理推论,方程本身为线性方程为正定,平衡点处微分方程负定,则系统平衡点p0(1,0,0,0)是Lyapunov渐近稳定的。
2)风险爆发平衡点及稳定性。
根据系统平衡点的定义,需满足平衡点位置所有变量的微分为0,即
(5)
解得:
(6)
当T≥1时,I≤0,结合假设,取I=0,此时T=1,系统存在唯一平衡点,即上文所讨论的风险规避平衡点。说明在机场飞行区人为风险传染系统中,随着时间的增加,人为风险对系统的影响逐渐减弱,并最终得到有效规避。
当T<1时,系统存在唯一正平衡点,风险爆发平衡点
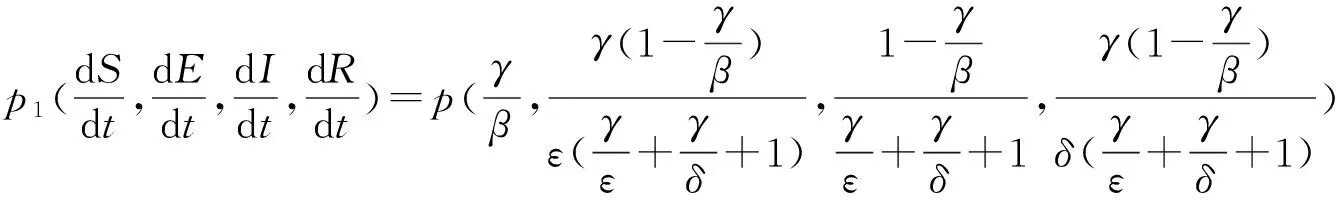
(7)


(8)
求解该矩阵的特征方程,解得

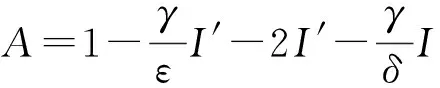
λ*3+(βI′+ε+γ+δ)λ*2+(βγI′+βδI′+εγ+εδ+γε-βεA-βεI′)λ*+(βγδI′+εγδ-βεδA)=0。
(9)
(10)

通过分析可知,机场人为风险系统中个别风险凸显时,并不一定会大面积传染,只有当系统达到阈值时,人为风险才会传播开来。
2 模型仿真分析
本文运用Matlab软件进行机场飞行区人为风险传染过程的仿真研究。
2.1 参数假设
根据前文假设,β为染病的风险源的传染率,ε为潜伏群体被传染且病症显现而转化为感染群体的比例,γ为感染群体转化为免疫群体的比例,δ为免疫群体因免疫能力变弱而转化为易感群体的比例,结合机场飞行区实际工作情况,分别对β、ε、γ和δ作出假设:β=0.04,ε=0.07,γ=0.85,δ=0.41。由于机场工作环境和内容的特殊性,往往风险出现的可能性较小,一旦发生,较为严重,且与环境互动导致的易感群体在传染源中的暴露程度往往较大,但风险源间的相互作用可能性较小。结合这些特征,在对参数进行假设时,传染率相对较小;染病率大于传染率,即被传染后有更大的可能出现病症;一旦风险爆发,不安全事件发生,其管控措施将被严格记录下来,二次感染时能快速作出反应,因此γ值较大;而机场所处环境多变,易感群体的暴露程度较大,且风险易出现变异,因此δ值较大。

(11)
2.2 仿真结果分析
1)传染初期仿真。
分别设定x1,x2,x3的初始值为0.31,0.15,0.10,可见此时的系统尚处于染病的初期,此时易感人群数量最多,免疫群体最少,设定仿真周期为[0,30],编写Matlab编码,得到如图1所示的结果。
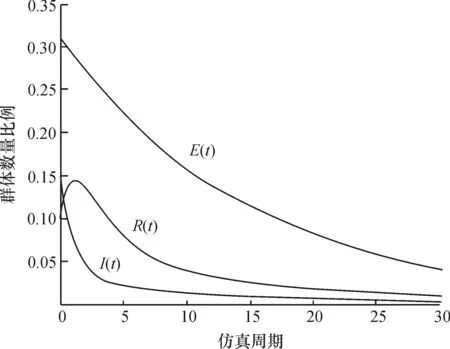
图1 传染初期仿真结果Fig.1 Simulation result of the infection early stage
由仿真结果可以看出,机场飞行区人为风险在传染初期时,潜伏群体、感染群体和免疫群体随着时间的推移,最终达到相对平衡的状态。其中免疫群体在初期将出现较短时间的快速增加,这与机场风险预案的完备是相关的。但由于风险种类的变异和风险预案库的局限性,免疫群体在出现增长的高峰之后会迅速回落,最终免疫群体趋于零平衡。
潜伏群体则呈较为平滑的递减趋势。而感染群体则是在最初系统非特异性免疫,即系统的应激反应产生影响急速减少后,当特异性免疫,即系统的稳态反应起作用后减速逐渐放缓,最终趋于零平衡。
因此,在机场飞行区人为风险的传染初期防疫工作中,应把握免疫群体快速增加和感染群体快速减少的阶段,即做好系统抗原入侵时初次应答的非特异性免疫能力和多次应答的预案匹配。结合人为风险的特征,在机场日常管理中,通过增强工作人员的业务能力、风险应对能力和心理素质等措施提升系统的非特异性免疫能力。在风险初次发生时,应及时采取有效的管控措施,形成风险预案,提高多次应答预案的匹配度。
2)传染中期仿真。
分别设定x1,x2,x3的初始值为0.20,0.51,0.13,可见此时的系统处于染病的中期,此时易感人群数量减少,免疫群体仍最少,感染群体数量最多,设定仿真周期为[0,30],编写Matlab编码,得到如图2所示的结果。

图2 传染中期仿真结果Fig.2 Simulation result of the infection middle stage
当系统进入传染中期后,潜伏群体、感染群体和免疫群体随着时间的推移,均趋于达到零平衡,系统中将出现易感人群占大部分比例的平衡状态。潜伏群体在传染中期呈平缓的减少趋势;感染群体与传染初期类似,出现急速的减少后,初见趋于平缓减少趋势,直至趋近于0;免疫群体则在短期的急速增加后,急速减少,最终趋于零平衡。
由此可见,在机场飞行区人为风险系统处于传染中期时,应尽量延长免疫群体快速增加和感染群体快速减少的阶段,加强非特异性免疫预案库的匹配程度。同时加快特异性免疫的反应速度,增加特异性免疫的免疫能力。在机场的风险管理中,应注重工作人员心理素质和生理素质的锻炼,提高其应对风险的灵活性和风险预案的可操作性,优化风险管控流程,从而提升预案匹配度和免疫反应速度。
3)传染后期仿真。
分别设定x1,x2,x3的初始值为0.08,0.15,0.52,可见此时的系统处于染病的后期,此时免疫人群数量最多,潜伏群体最少,设定仿真周期为[0,30],编写Matlab编码,得到如图3所示的结果。

图3 传染后期仿真结果Fig.3 Simulation result of the infection late stage
在机场飞行区人为风险传染的后期,不同于初期和中期,潜伏群体在急速减少后呈缓慢的增加趋势,最终趋于零平衡,但低于0的情况与本文假设相悖,仅就其变化趋势进行分析。
由变化趋势可以看出,潜伏群体在短时间内被快速感染并治愈,成为免疫群体或易感群体。可见,机场人为风险系统在风险传染的后期,应做好潜伏群体的防疫工作,关注人员的情绪和行为变化,一旦出现异常,及时进行干预和疏导,避免潜伏群体病症的大面积爆发,威胁系统安全。
3 结论
由于机场飞行区人为风险具有一定潜伏期,且在完全爆发前存在隐性状态,故本文采用SEIRS传染病模型进行风险传染过程的分析,将风险分为易感群体、潜伏群体、感染群体和免疫群体4类。建立机场飞行区人为风险传染病微分模型,模型分别存在风险爆发和风险规避的平衡点,且在平衡点渐进稳定。通过分析可知,机场人为风险系统中个别风险凸显时,并不一定会大面积传染,只有当系统达到阈值时,人为风险才会传播开来。
运用Matlab软件进行机场飞行区人为风险传染过程仿真,结果表明潜伏群体、感染群体和免疫群体随着时间的推移,最终均达到相对平衡的状态。其中,对于易感群体而言,应通过提升其业务技能、强化心理和生理素质、和谐团队关系等加强其遗传免疫力,避免风险感染的可能;潜伏群体是风险监测的重点对象,实时监测各项风险指标,一旦突破阈值,即转化为感染群体,潜在的风险显现出来,应及时采取有效的风险管控的措施,启动飞行区人为风险系统的特异性免疫和非特异性免疫;感染群体则为风险管控的重点对象,通过管理手段等干预疗法提升其免疫性,将其转化为免疫群体;而免疫群体在免疫期内是相对安全的,因此对其免疫期限的评估和监管则较为重要,一旦免疫能力失效,则转化为易感群体。可通过风险管控方案的不断完善和已发风险所形成的预案的演习等手段延长免疫群体的免疫期。具体各阶段风险群体的变化规律如下。
1)风险传染初期,免疫群体由于机场风险管控预案的实施在较短时间内快速增加,预案库的局限性导致免疫群体在快速增加后迅速回落,最终趋于零平衡。潜伏群体呈较为平滑的减弱趋势。感染群体初期由于机场风险管控系统的应激反应急速减少后,在系统稳定反应的作用下降低的速度逐渐放缓,最终趋于零平衡。可见,在风险传染初期,应尽可能延长免疫群体快速增长和感染群体快速减少的阶段,即加强机场非特异性免疫系统的建设,完善风险管控预案库,提高管控预案的可操作性和应激性,做好抗原入侵的初次应答和多次应答的预案匹配。
2)风险传染中期,系统平衡状态下易感群体将占较大比例。各群体变化趋势与初期类似,但速率有所差异。可见,在风险传染中期,应进一步加大非特异性免疫预案库与风险的匹配程度,并加强特异性免疫的反应速度和免疫能力,缩短风险在特异性免疫前夕的传染时间,减小传染力度。
3)风险传染后期,潜伏群体在短时间内被快速感染并治愈,成为免疫群体或易感群体。潜伏群体急速减少后呈缓慢的增加趋势,最终趋于零平衡。可见,在风险传染后期,应做好潜在风险的排查,关注人员的情绪和行为异常,积极进行心理疏导和干预,避免潜在风险爆发威胁系统安全。
[1]TONZER Lena. Cross-border interbank networks, banking risk and contagion[J]. Journal of Financial Stability, 2015, 18(6): 19-32.
[2]LADLEY Daniel. Contagion and risk-sharing on the inter-bank market[J]. Journal of Economic Dynamics & Control, 2013, 37(7): 1384-1400.
[3]ALBULESCU Claudiu Tiberiu, GOYEAU Daniel, TIWARI Aviral Kumar. Contagion and dynamic correlation of the main European stock index futures markets: a time-frequency approach[J]. Procedia Economics and Finance, 2015, 20(3): 19-27.
[4]AKAY Ozgur (Ozzy), SENYUZ Zeynep, YOLDAS Emre. Hedge fund contagion and risk-adjusted returns: a Markov-switching dynamic factor approach[J]. Journal of Empirical Finance, 2013, 22(6): 16-29.
[5]SUH Sangwon. Measuring sovereign risk contagion in the Eurozone[J]. International Review of Economics and Finance, 2015, 35(1): 45-65.
[6] 陈庭强,何建敏.基于复杂网络的信用风险传染模型研究[J].软科学,2014,28(2):111-117.
CHEN Tingqiang, HE Jianmin. Credit risk contagion model based on complex network[J]. Soft Science, 2014, 28(2): 111-117.
[7]GAGLIARDINI Patrick, GOURIÉROUX Christian. Correlated risks vs contagion in stochastic transition models[J]. Journal of Economic Dynamics & Control, 2013, 37(11): 2241-2269.
[8]谢赤,王彭,杨姣姣,等.基于DCC-MSV-KMV模型的第三产业行业信用风险传染效应度量[J].湖南大学学报(自然科学版),2013,40(10):111-116.
XIE Chi, WANG Peng, YANG Jiaojiao, et al. Measurement of the credit risk contagion effects between the sectors in the tertiary industry based on DCC-MSV-KMV model[J]. Journal of Hunan University (Natural Sciences), 2013, 40(10): 111-116.
[9]MARTINEZ-JARAMILLO Serafin, PÉREZ Pérez Omar, EMBRIZ Fernando Avila, et al. Systemic risk, financial contagion and financial fragility[J]. Journal of Economic Dynamics & Control, 2010, 34(11): 2358-2374.
[10]CAO Huaihu, ZHU Jianming. Research on banking crisis contagion dynamics based on the complex network of system engineering[J]. Systems Engineering Procedia, 2012, 5(4): 156-161.
[11]HAUSENBLAS Václav, KUBICOVA Ivana, LESANOVSKA Jitka. Contagion risk in the Czech financial system: a network analysis and simulation approach[J]. Economic Systems, 2015, 39(1): 156-180.
[12] 陈建新,罗伟其,庞素琳.银行风险传染的集合种群模型——基于元胞自动机的动态模拟[J].系统工程理论与实践,2012,32(3):543-548.
CHEN Jianxin, LUO Weiqi, PANG Sulin. The risk infection for the bank of met population model-based on the dynamic simulation of the cellular automata[J]. System Engineering-Theory & Practice, 2012, 32(3): 543-548.
[14]ASGHARIAN Hossein, NOSSMAN Marcus. Risk contagion among international stock markets[J]. Journal of International Money and Finance, 2011, 30(1): 22-28.
[15]BEIRNE John, FRATZSCHER Marcel. The pricing of sovereign risk and contagion during the European sovereign debt crisis[J]. Journal of International Money and Finance, 2013, 34(4): 60-82.
[16]FONG Tom Pak Wing, WONG Alfred Y-T. Gauging potential sovereign risk contagion in Europe[J]. Economics Letters, 2012, 115(3): 496-499.
[17]BOUDREAULT Mathieu, GAUTHIER Geneviève, THOMASSIN Tommy. Contagion effect on bond portfolio risk measures in a hybrid credit risk model[J]. Finance Research Letters, 2014, 11(2): 131-139.
[18]卢盛.基于复杂网络理论的航空货运系统鲁棒性分析[D].吉林:吉林大学,2014.
LU Sheng. Robust analysis of aviation logistics system based on complex network theory[D]. Jilin: Jilin University, 2014.
[19]赵贤利,罗帆.基于复杂网络理论的机场飞行区风险演化模型研究[J].电子科技大学学报(社科版),2013,15(4):31-34.
ZHAO Xianli, LUO Fan. Research on the risks evolution model based on complex networks in airport flight area[J]. Journal of UESTC(Social Sciences Edition), 2013, 15(4): 31-34.
[20]赵贤利,罗帆.基于系统动力学的跑道侵入风险演化博弈研究[J].工业工程,2015,18(2):73-79.
ZHAO Xianli, LUO Fan. A research on evolutionary game of runway incursion risks based on system dynamics[J]. Industrial Engineering Journal, 2015, 18(2): 73-79.
[21]许红军,田俊改.通用航空安全体系自组织演化动力学机制与模式研究[J].中国安全生产科学技术,2012,8(3):135-140.
XU Hongjun, TIAN Jungai. Research on dynamics mechanism and mode of general aviation safety management system self-organizing evolvement[J]. Journal of Safety Science and Technology, 2012, 8(3): 135-140.
[22]周站. 员工离职恐慌的传染机理与免疫机制研究[D].武汉:武汉理工大学,2010.
ZHOU Zhan. Study on mechanisms of employee turnover panic′s contagion and immune[D]. Wuhan: Wuhan University of Technology, 2010.
[23]马颖,张园园,宋文广.食品行业突发事件风险感知的传染病模型研究[J].科研管理,2013,34(9):123-129.
MA Ying, ZHANG Yuanyuan, SONG Wenguang. Research on epidemic model of emergency events risk perception in food industry[J]. Science Research Management, 2013, 34(9): 123-129.
[24]王砚羽,谢伟.基于传染病模型的商业模式扩散机制研究[J].科研管理,2015,36(7):10-18.
WANG Yanyu, XIE Wei. A study on the diffusion mechanism of business model based on the Epidemic model[J]. Science Research Management, 2015, 36(7): 10-18.
[25]樊治平,刘洋,沈荣鉴.基于前景理论的突发事件应急响应的风险决策方法[J].系统工程理论与实践,2012,32(5):977-984.
FAN Zhiping, LIU Yang, SHEN Rongjian. Risk decision analysis method for emergency response based on prospect theory[J]. System Engineering-Theory & Practice, 2012, 32(5): 977-984.
[26]Dell’OLIO Luigi, IBEAS Angel, BARREDA Rosa, et al. Passenger behavior in trains during emergency situations[J]. Journal of Safety Research,2013,46:157-166.
[27]王亚奇,蒋国平.考虑交通流量的复杂网络病毒传播行为研究[J].系统工程学报,2010,25(6):773-778.
WANG Yaqi, JIANG Guoping. Epidemic spreading on complex networks with traffic flow[J]. Journal of Systems Engineering, 2010, 25(6): 773-778.
[28]王治莹,李勇建.舆情传播与应急决策的结构化描述及其相互作用规律[J].系统工程理论与实践,2015,35(8):2064-2073.
WANG Zhiying, LI Yongjian. Structural description and interaction law of public opinion propagation and emergency decision-making[J]. System Engineering-Theory & Practice, 2015, 35(8): 2064-2073.
[29]夏承遗,马军海,陈增强.复杂网络上考虑感染媒介的SIR传播模型研究[J].系统工程学报,2010,25(6):818-823.
XIA Chengyi, MA Junhai, CHEN Zengqiang. SIR epidemic model with infection medium on complex networks[J]. Journal of Systems Engineering, 2010, 25(6): 818-823.
InfectionProcessofAirportFlightAreaHumanRiskBasedonSEIRSEpidemicDiseaseModel
TANG Xinxin,LUO Fan
(School of Management, Wuhan University of Technology, Wuhan 430070,China)
Infectious process model of airport flight area human risk is constructed based on SEIRS (susceptible-exposed-infected-recovered-susceptible) epidemic disease model for risk management and control in a more scientific and rational way. The assumptions of the model are defined. The equilibrium point and stability of the model are analyzed. The model is asymptotically stable at the equilibrium point. Model simulation results by Matlab software shows that latent group, infected group and immune group all finally tend to zero balance no matter in the early stage, the middle stage or the late stage of the risk of infection. Latent group shows a relatively smooth decreasing trend. Infected group tends to zero balance after rapid decline. Immune population has a rapid growth in the short term after the rapid decline. There is a significant difference in the rate of change of different groups at different stages. Latent group shows a slow upward trend till zero balance after the rapid decline in the last stage. The conclusion provides the theoretical basis for the strategic focus of different stages of risk management and control.
human risk; risk infection; airport flight area; epidemic disease model
2016- 07- 08
国家自然科学基金资助项目(71271163)
唐辛欣(1987-),女,湖北省人,博士研究生,主要研究方向为风险预警管理、人力资源管理.
10.3969/j.issn.1007- 7375.2016.06.009
X
A
1007-7375(2016)06- 0056- 08

