小波分频及其在海洋地震数据瞬时属性提取中的应用
刘 洋, 黄光南
(1.东华理工大学放射性地质与勘探技术国防重点学科实验室,江西 南昌 330013;2.东华理工大学地球物理与测控技术学院地球物理系,江西 南昌 330013)
小波分频及其在海洋地震数据瞬时属性提取中的应用
刘 洋1,2, 黄光南1,2
(1.东华理工大学放射性地质与勘探技术国防重点学科实验室,江西 南昌 330013;2.东华理工大学地球物理与测控技术学院地球物理系,江西 南昌 330013)
小波变换是用伸缩和平移小波形成的小波基来分解或重构时变信号的一种信号处理方法。将小波变换运用于地震数据分析,其目的是在时频域内细致地分析地震记录的时变特性,以获得详细的有用地质体信息。针对墨西哥湾海域地震数据噪音干扰大、分辨率有限的问题,应用小波分频的方法对该海域的地震数据进行处理并提取其瞬时属性,结果表明该方法具有很好的时频分辨能力,可有效压制噪音干扰,提高地震记录的分辨率,在确定地质体分布以及识别地质体的构造特征方面,取得了理想的效果。
小波变换;信号分解与重构;瞬时振幅;瞬时相位;瞬时频率
小波变换经历了数次跳跃式的发展,并取得了丰硕的科研成果(周伟等,2006; 彭丹,2014)。小波函数起源于Harr小波,其为一组相互正交归一的函数集,数学家对傅里叶级数进行二进制的分解,从而建立了二进制频率分量的分组理论(Littlewood,1931)。随后Y.Meyer在偶然间构造出了小波基,并从理论上证明了一维小波函数的存在,并与S.Mallat合作共同给出了分解及重构的快速算法—Mallat算法(Mallat,1989),由此小波分析才开始蓬勃发展起来。传统的卷积小波运算过程复杂、计算量巨大,不便于在计算机上实现快速运算。20世纪末新式小波变换被创造出来,克服了旧式小波的平移与伸缩的不可变性,计算简单且快速,并进一步增强了其适用性(Sweldens,1995)。
利用小波变换的时间和频率特性,可以实现地震记录的分频处理(黄捍东等,2008;高爱荣等,2014)。应用小波变换的多尺度特性,对不同尺度的地震信号进行分离,经过小波分频处理后可以得到不同频段的高分辨率数据(马朋善等,2007),而地震属性分析最早可以追溯到1940年代,它是信号分析快速发展的产物。1970年代,Taner将复地震道分析与提取瞬时属性法应用于地震剖面的处理,随后我国科研人员也加大研究力度,取得了理想效果(王西文等,2000;张宇等,2014)。复地震道分析法主要是分析地震的瞬时属性剖面,即瞬时振幅、瞬时相位、瞬时频率剖面,故也称之为三瞬时属性法(邱陶兴等,1991)。本文将小波分频以及三瞬时属性法相结合,将其应用于墨西哥湾海域噪音干扰较大的海洋地震数据处理中,取得了显著效果。
1 小波变换的理论
1.1 连续小波变换的基本原理
对任意函数f(t)=L2(R),其小波变换定义为:
W(a,b)=[f(t),ψa,b(t)]=
(1)
不同的a和b构成的小波基函数为:
(2)
满足约束条件:
(3)
若尺度因子a>1,则小波基函数在时域的波形被拉伸,它的频谱在变窄的同时向低频方向移动,其多分辨率特性为大的尺度参数对应于低频端,频率分辨率越高,时间分辨率越低。式中b为平移因子。函数经过小波变换,将其投影到时间-尺度相平面上,使得有利于提取信号中的有用成分。小波变换就是通过伸缩平移运算逐步对信号进行多尺度细化,最终达到高频处时间细分,低频处频率细分,能自动适应时频信号分析的要求,从而可聚焦到信号的任意细节。实质上是运用不同尺度的小波基将信号分解到相应的频段,尺度因子越小,其对应频带的中心频率越高。
1.2 常用的基本小波
傅里叶分析方法是将一个信号分解成各种不同频率的正弦波,所以正弦波是傅里叶变换的基函数。与之相仿,小波分析是将一个信号分解成由原始小波通过位移和缩放后的一系列小波,因此小波是小波变换的基函数。小波函数多以开发者的名字命名。
(1)Haar小波
Haar函数是一组相互正交归一的函数集。Haar小波是由其衍生得到且为全部已知小波中最简单的。它是支撑范围中的单个矩阵波。
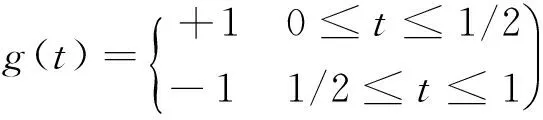
(4)
(2)高斯小波
高斯小波是高斯函数的一阶导数:
(5)
dbNg(ω)=iωe-ω2/2
(6)
高斯小波具有良好的时间、频率局部特性:关于0轴反对称。它在信号与图像的边缘提取中具有十分广泛的应用。
(3)Daubechies (dbN) 小波系
Daubechies小波它是由著名的小波分析专家Inrid Daubechies构造的小波函数,通常写为dbN,N表示为小波阶数。dbN小波函数中尺度函数φ与小波函数ψ的有效支撑长度为2N-1,小波函数ψ的时矩为N,因此这个序列的小波扩展性较好,可以灵活地权衡由增加支集长度引起的边界问题。
1.3 地震数据瞬时属性的提取
地震信号是一种非稳态信号,其振幅、相位、频率都是随时间变化而发生改变的函数。通过振幅、相位、频率等参数不但可以描述出任何一种地震波的状态,而且从中可以体现出地质体的相关信息。所以对地震信号瞬时参数的提取,有利于准确地认识地质体的分布及作出合理地质解释。
地震信号为实信号,其计算其瞬时参数的基本步骤为:首先构造出地震信号的复信号;其次利用解析信号法直接求出瞬时振幅、瞬时相位、瞬时频率等参数。对于一个实际的地震道x(t),其相对应的复数道:
R(t)=x(t)+ih(t)
(7)
其中:
(8)
那么,常规复数道分析方法中各参数的数学表达式为:
瞬时振幅:
A(t)=[x2(t)+h2(t)]1/2
(9)
瞬时相位:
(10)
瞬时频率:
(11)
计算地震信号相对应的复信号方法有很多种,但是实际地震数据处理的过程中,通常选用的方法是Hilbert变换的方法:首先计算地震实信号的Hilbert变换,将其作为复信号的虚部;然后将待分析的地震信号作为复信号的实部;最后将构成的复信号直接计算出瞬时属性。在对同一个区域内进行探测,通过以上公式的计算,若其瞬时振幅、瞬时相位以及瞬时频率相比较而言发生了明显 的改变,通常可以断言:该探测区域存在着岩石物理性质的改变(徐敬领等, 2010)。瞬时振幅可用于判断岩性变化,例如局部断层,不整合面,油气富集带等。瞬时相位可清晰反应断层,超覆、尖灭等岩性圈闭。瞬时频率可推断气层和裂缝的存在,由于瞬时频率在薄层处数值会偏高,故在薄层显示不明显的常规地震剖面上,可以用来识别薄层(石颖等, 2008; 高静怀等, 2005)。
1.处理好审与被审的关系。能否处理好与被审计对象工作上的沟通协调问题,直接影响着审计组的工作质量和效率。审计组长要引导审计组成员树立“监督是手段,服务是目的”的理念,以一种平等待人的态度,不卑不亢,既不以势压人,也不低三下四。比如,在对被审计单位进行审计过程中,要注重发挥审计的监督性作用,同时也要发挥审计的建设性作用,既要对服务对象工作中取得的成绩予以肯定,同时也要指出工作中存在的问题,取得被审计单位的理解、支持与配合,构建和谐的审与被审关系。
2 模拟信号的小波分频
以下是由Matlab语言模拟出的含噪音信号。图1中,x为含噪音的模拟信号,将用’db3’小波将含噪音信号分解为3层。a1-a3为小波分解的第一层至第三层低频信号。图2中,d1-d3为小波分解的第一层至第三层高频信号。
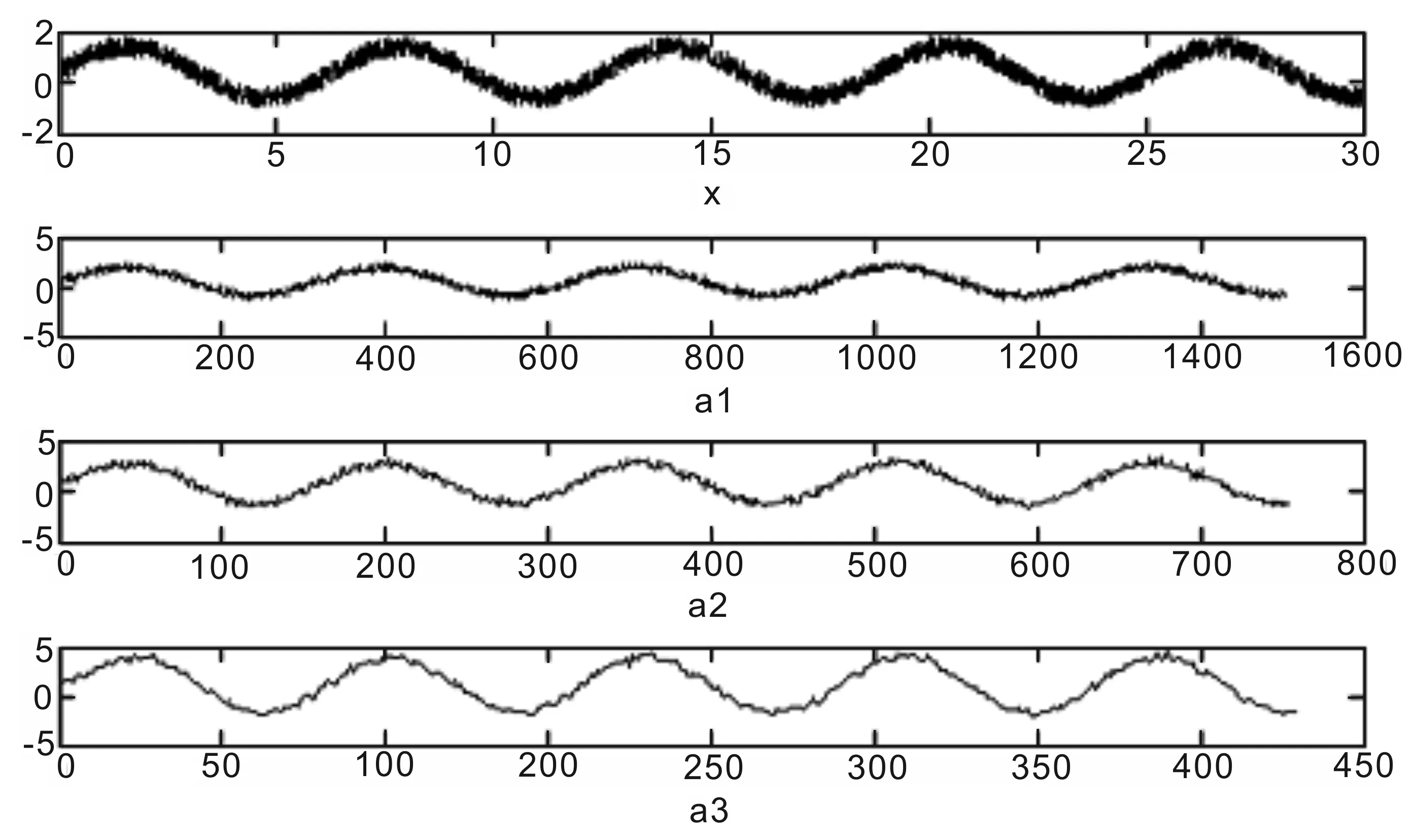
图1 理论信号低频分解Fig.1 The theory signal of low frequency decomposition

图2 理论信号高频分解Fig.2 The theory signal of high frequency decomposition
通过以上对理论模拟的噪音信号进行小波分解,可去除噪音对主频信号的影响,清晰准确地分析模拟信号的各个成分,即含噪音的模拟信号主要是由低频的正弦信号以及高频的随机干扰信号构成。
3 海洋地震数据的瞬时提取
图3是在墨西哥湾海域使用浅震源激发,接收电缆沉放深度较大的海洋单道地震反射剖面。其中,0.77 s处的同相轴为海底平面,由于电缆产生干扰噪音能量远远超过从海底及以下平面传回的有效信息能量,导致海底平面以下的地质体分布情况并不能从此地震反射剖面中清晰地获得。本文首先将80道地震记录剖面的每一道依次用“db4 ”小波进行低频分解及高频分解;然后将已经进行了低频及高频分解的每一道地震记录按地震道号再进行小波重构,形成新的低频及高频地震记录剖面;最后根据低频及高频剖面各自绘制其瞬时振幅、瞬时相位、瞬时频率剖面图。
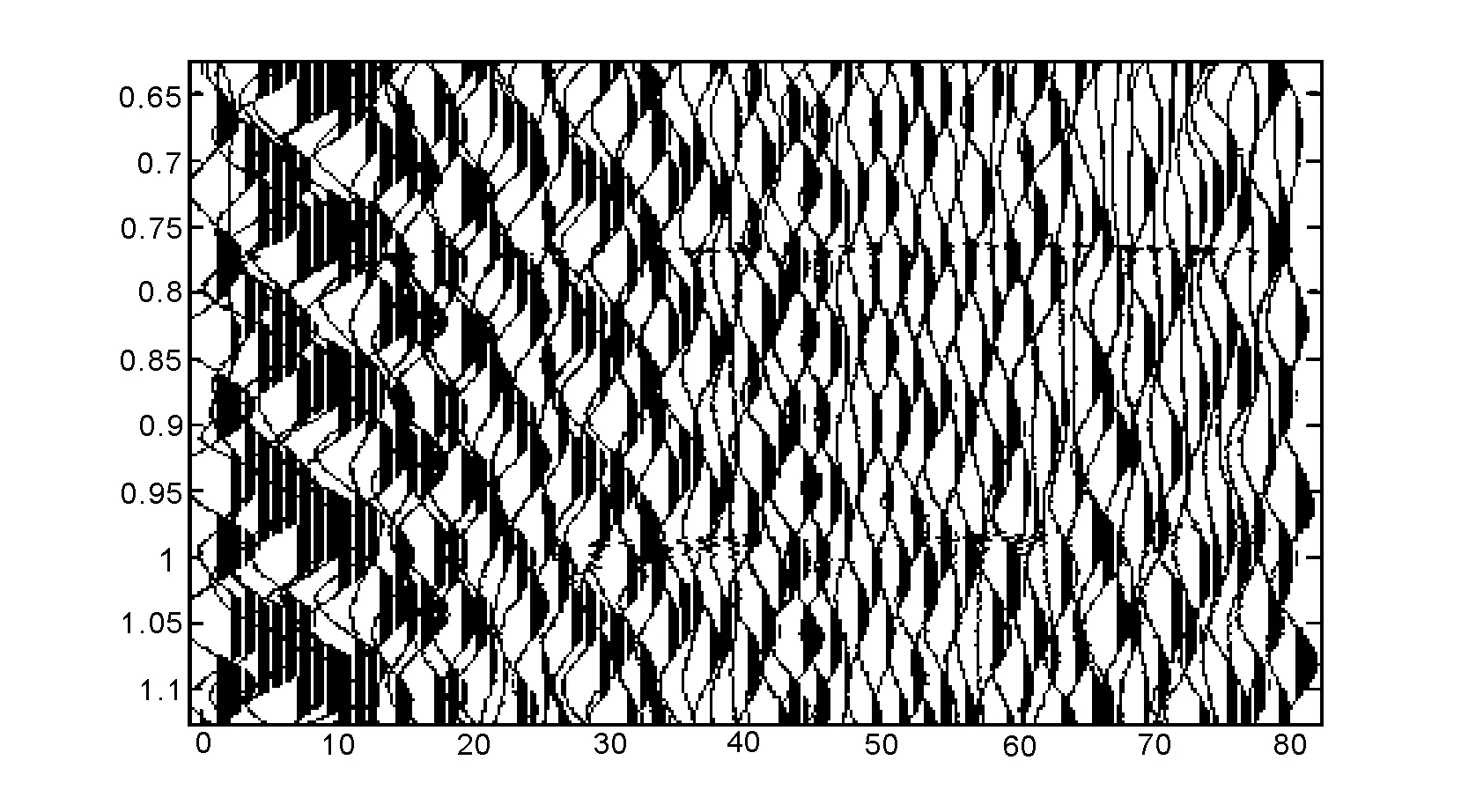
图3 海洋单道地震剖面Fig.3 The single-channel profile of marine seismic

图4 海洋单道地震剖面的低频成分 Fig.4 Low-frequency components of single-channel marine seismic profile

图5 海洋单道地震剖面的高频成分Fig.5 High-frequency components of single-channel marine seismic profile
图4是海洋单道地震剖面的低频成分,其中虽然含有很强的低频电缆及人为噪音干扰,但仍然包含少量的有效海底地层反射信息。图5是海洋单道地震剖面的高频成分,此剖面图不仅可清晰地反应0.77 s处的海底平面,而且在1 s处反应了部分海底地质体的分布情况。
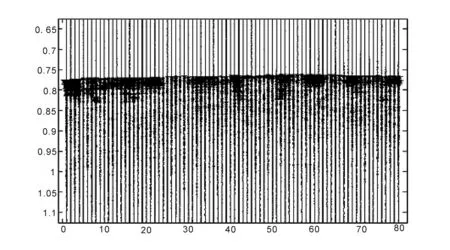
图6 海洋单道瞬时振幅属性剖面Fig.6 The single-channel profile of the instantaneous amplitude
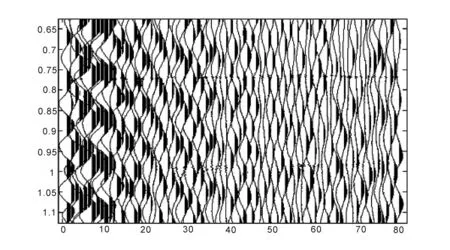
图7 低频成分的瞬时振幅属性剖面Fig.7 The low-frequency instantaneous amplitude profile
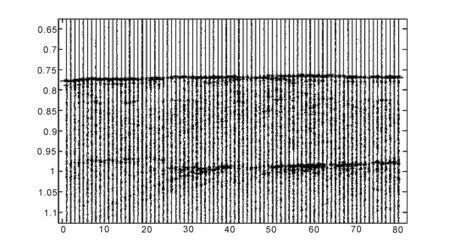
图8 高频成分的瞬时振幅属性剖面Fig.8 The high-frequency instantaneous amplitude profile
图6为海洋单道瞬时振幅属性剖面,其中海底平面瞬时振幅明显,海底平面以下的地质体分布情况则完全没有体现。 图7与图8分别是低频及高频成分的瞬时振幅属性剖面,瞬时振幅的大小与反射波的能量强度有着密切的联系,主要体现能量上的改变。在高频成分的瞬时振幅属性剖面中,可通过瞬时振幅的改变来判岩石的物理性质的变化。
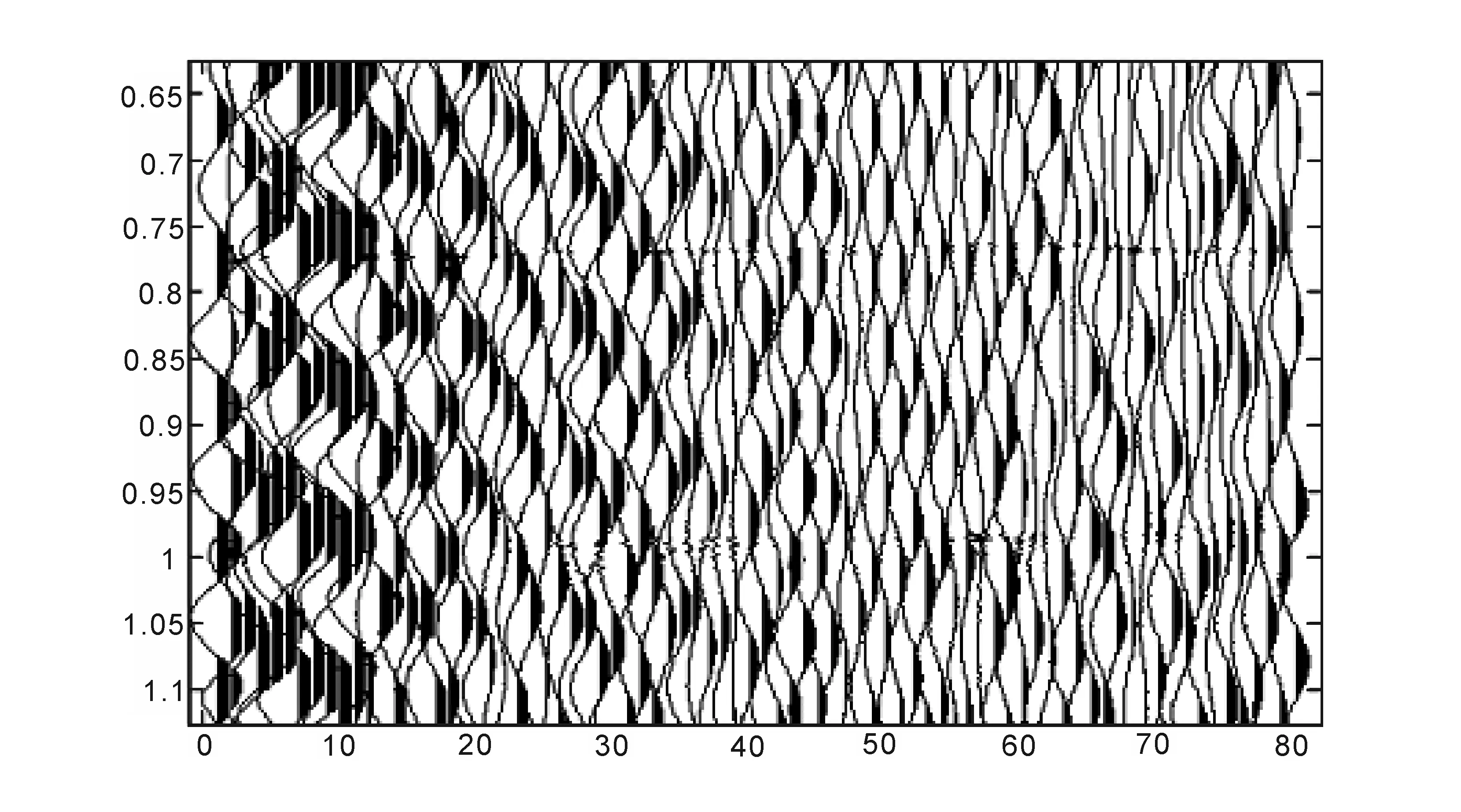
图9 海洋单道瞬时相位属性剖面Fig.9 The single-channel profile of instantaneous phase

图10 低频成分的瞬时相位属性剖面Fig.10 The low-frequency instantaneous phase profile

图11 高频成分的瞬时相位属性剖面Fig.11 The high-frequency instantaneous phase profile
图9为海洋单道瞬时相位属性剖面,其对于海底平面及以下地质体分布的体现并不突出。 图10 与图11分别是低频及高频成分的瞬时相位属性剖面,瞬时相位是某一时刻子波真实相位的度量,其对反射强度较弱的地震波有明显的体现。若瞬时相位剖面中出现中断时,可以断定在此处存在地质体异常或识别层位信息。但在对此海域进行瞬时相位属性剖面的提取时,无论是低频还是高频成分在对反射强度较弱的地震波并没有十分清晰的体现。
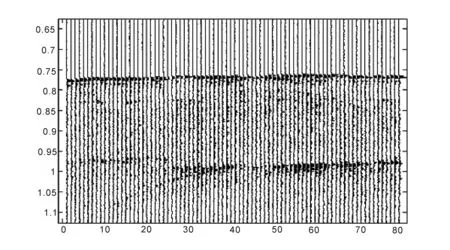
图12 海洋单道地震瞬时频率属性剖面 Fig.12 The single-channel profile of instantaneous frequency

图13 低频成分的瞬时频率属性剖面 Fig.13 The low-frequency instantaneous frequency profile
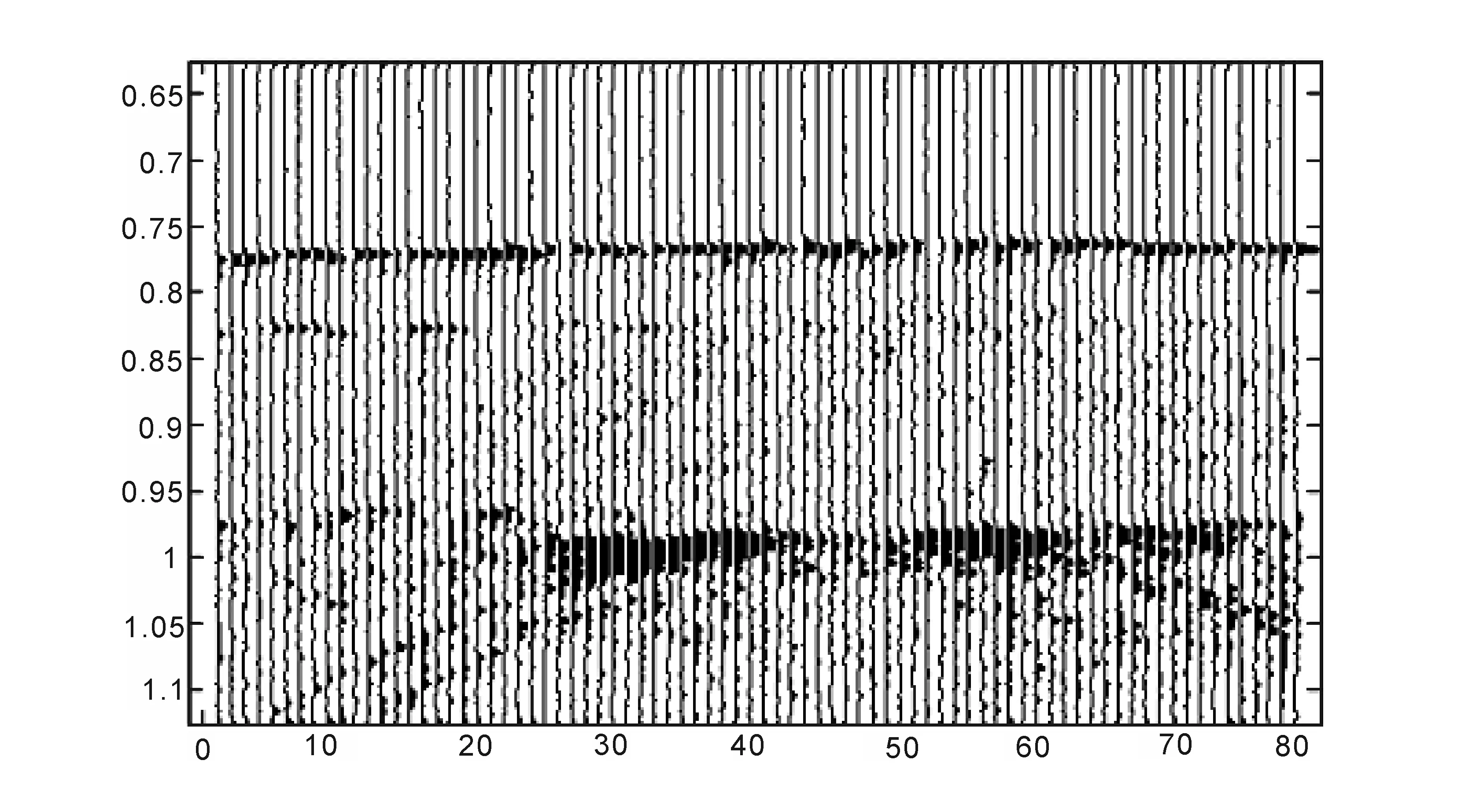
图14 高频成分的瞬时频率属性剖面Fig.14 The high-frequency instantaneous frequency profile
图12为海洋单道地震瞬时频率属性剖面,其海底平面及以下地质体结构已相对清晰。图13与图14分别是低频及高频成分的瞬时频率属性剖面,瞬时频率是根据对地震道中的频率作逐点抽样得到的,相当于对瞬时相位做时间的导数。其特点为地震波在地下传播时,遇到不同的地质体时频率会随之发生改变,此改变可以清楚的显示在瞬时频率的剖面上,同样可以用来反映地层的岩石性质变化以及识别地层。在此瞬时频率属性剖面提取中,其低频部分含有低频噪音干扰使得该剖面并不清晰,但高频成分的瞬时频率剖面已经能很清晰地反应该海域海底地质体的分布。综上所述通过各个剖面的提取有利于确定此海域内海底地质体分布情况并作出合理解释。
4 结论
通过对理论信号以及实际海洋地震记数据进行小波变换、分解并提取其瞬时属性可得出以下结论:本文的研究方法是小波分频与三瞬时属性法的结合,其结果表明该方法具有很好的时频分辨能力,在确定地质体分布方面,取得了理想效果。通过对该海域海洋地震数据的处理,理论上可通过瞬时振幅及瞬时频率判断出地下地质体的大致位置,再通过瞬时相位确定其地质体的边界,但在进行瞬时相位属性剖面的提取时,无论是低频还是高频成分效果并不十分明显,这其中的原因可能是地质体的复杂结构以及岩石物理性质的骤然改变等各种因素引起的,这就要求结合其他地质资料或者借助其他技术手段做进一步的深入研究。
高爱荣, 秦广胜. 2014. 地震资料分频处理及应用[J]. 内蒙古石油化工,14(1): 11-12.
高成, 董长虹, 郭磊, 等.2007. Matlab小波分析与应用[M]. 北京: 国防工业出版社:22-78.
高静怀, 陈风, 陈树民. 2005. 利用地震瞬时属性进行薄互层分析[J].煤田地质与勘探, 33(3):67-70.
何光明, 高如曾, 韩德贵, 等. 1996.小波变换在地震资料高分辨处理中的应用[J]. 石油物探,35(2):44-54.
黄捍东, 张如伟, 郭迎春. 2008. 地震信号的小波分频处理[J]. 石油天然气学报, 30(3): 87-91.
马朋善, 高秀花, 汪桂春. 2007. 小波分析在地震资料分频处理中的应用[J]. 特种油气藏,14(3):35-39.
彭丹.2014.小波分析概述及其应用研究[J]. 装备制造技术, 6(2):145-147.
齐宇, 刘震, 魏建新, 等. 2010. 基于小波变换的谱分解技术在地震模型解释中的应用[J]. 新疆石油地质, 31(4):417-419.
邱陶兴, 廖其林, 王振明. 1991. 三瞬剖面法在人工地震测深中的应用研究[J]. 地震研究, 14(3):247-256.
石颖, 刘洪. 2008. 地震信号的复地震道分析及应用[J].地球物理学进展,23(5):1538-1543.
王西文, 刘全新, 李幼铭, 等.2000. 地震信号瞬时特征在小波域分频提取的方法和应用[J]. 石油地球物理勘探, 35(4):453-460.
徐敬领,刘洛夫,王贵文,等.2010. 应用测井资料的“三瞬属性”进行地层划分及对比研究[J]. 地球科学进展, 25(4):408-417.
张宇, 康建红, 庞晶源, 等. 2014. 地震信号高精度谱分解方法综述[J]. 防灾减灾学报, 30(1): 91-95.
周伟, 桂林, 周林. 2006. Matlab小波分析与高级技术[M]. 西安: 西安电子科技大学出版社:26-43.
Littlewood, Paley. 1931. Theorems on Fourier Series and Power Series [J]. London Math, 6(3): 230-233.
Mallat.1989. Multiresolution approximations and wavelet orthonormal bases of[J].Transactions AMS, 315(1): 69-87.
Satish Sinha, Partha S.Routh, Phil D.Anno. 2005. Spectral decomposition of seismic data with continuous-wavelet transform[J]. GEOPHYSICS, 70(6):19-25.
Wim Sweldens. 1995.Geek Page-Wavelet Image Compression: Beating the bandwidth bottleneck[J]. Wired. Retrieved, 132(5):18-34
Wavelet Decomposition and Its Application in Instantaneous Attribute’s Extraction for Marine Seismic Data
LIU Yang1,2, HUANG Guang-nan1,2
(1. Fundamental Science on Radioactive Geology and Exploration Technology Laboratory, East China University of Technology, Nanchang, JX 330013, China; 2. School of Nuclear Engineering and Geophysics, East China University of Technology, Nanchang, JX 330013, China)
Wavelet transform is a process of decomposing or reconstructing time-varying signals by using wavelet basis.Wavelet base consists of extended and translated wavelet functions. Apply wavelet transformation to the seismic data analysis, the purpose is to carefully in the time-frequency domain analysis of time-varying characteristic of seismic record, in order to obtain detailed information of geological body. In this paper, due to the problem of limited resolution of seismic data in Gulf waters, the application of the wavelet frequency method to deal with the area of seismic data and extract the instantaneous attributes, the results show that the method has good time-frequency resolution, which can effectively suppress the noise interference, improve the resolution of seismic record, in determining the distribution of geological body and identify the geological structure characteristics, the ideal results have been achieved.
Wavelet transform; Signal decomposition and reconstruction; The instantaneous amplitude; The instantaneous phase; The instantaneous frequency
2016-09-03
国家自然科学青年基金(41504095);核技术应用教育部工程研究中心基金(HJSJYB2015-9);东华理工大学博士科研启动基金(DHBK2013212)。
刘 洋(1992—),男,硕士生,主要从事地震资料信号处理与面波层析成像研究。E-mail: 497935238 @qq.com
10.3969/j.issn.1674-3504.2016.04.008
P631.4+4
A
1674-3504(2016)04-0352-10
刘洋,黄光南.2016. 小波分频及其在海洋地震数据瞬时属性提取中的应用[J].东华理工大学学报:自然科学版,39(4):352-361.
Liu Yang,Huang Guang-nan.2016. Wavelet decomposition and its application in instantaneous attribute’s extraction for marine seismic data[J].Journal of East China University of Technology (Natural Science), 39(4):352-361.
——工程地质勘察中,一种做交叉剖面的新方法

