波形特征的高斯混合模型锋电位分类算法

万 红 张 超 刘新玉 尚志刚

(郑州大学电气工程学院，郑州 450001)

波形特征的高斯混合模型锋电位分类算法

万 红*张 超 刘新玉 尚志刚

(郑州大学电气工程学院，郑州 450001)

锋电位分类是进行大脑信息处理机制研究的基本步骤之一。针对锋电位信号的复杂性和非平稳性，从统计聚类的角度出发，采用高斯混合模型描述锋电位信号的概率密度函数，提出了一种新的基于波形变化率特征和高斯混合模型聚类的锋电位分类方法。首先计算锋电位的波形变化率，然后利用最大差异方法获得锋电位波形的低维特征，最后采用高斯混合模型算法对特征进行聚类，实现锋电位分类。采用开放的仿真数据分析了该算法的分类精度和可行性，然后分别利用来自5只大鼠和1只恒河猴初级视觉皮层的实测数据验证了该算法的实用性，并与主成分分析特征的高斯混合模型聚类、幅值特征的高斯混合模型聚类和变化率特征的k均值聚类等3种方法进行了比较。仿真实验中，在噪声水平为0.05、0.10、0.15、0.20时，误分率分别为1.18%±1.18%、1.41%±1.06%、2.27%±1.51%、2.98%±2.06%, 低于其他3种方法；实测实验中，恒河猴数据的J3准则值为13.50±5.26，大鼠数据的J3准则值为26.43±10.46。与其他3种方法相比，平均J3准则值较大，且显著高于幅值特征的高斯混合模型聚类算法。所提出的方法表现出较高的分类精度和较好的类可分性，为实现神经元锋电位的可靠分类提供了一种有效的手段。

锋电位分类；波形变化率；最大差异算法；高斯混合模型

引言

在神经科学中，锋电位(spike)是神经信息接收、编码和传递的载体，具有重要的研究意义。在微电极阵列胞外记录方式中，每根微电极尖端可能被多个神经元包围，即一个电极可能同时记录到多个神经元发放的锋电位。因此需要首先把微电极阵列记录到的不同神经元的放电活动区分开来，即实现spike分类。然而在神经电生理实验中，神经信号会受到背景噪声的污染，使spike波形发生改变，增加了spike分类的难度。寻求简单高效的特征提取方法，进而实现精确的spike分类是目前神经信息编码机制研究一直致力解决的问题。

Spike分类一般包括带通滤波、检测、波形对齐、特征提取、降维和聚类等阶段。其中，特征提取是spike分类中至关重要的一步，特征提取的质量对分类结果有决定性作用。经典的特征提取方法主要提取spike的波形特征，如幅值、波宽、能量或相位[1-2]等，这种方法计算简单、效率较高，尤其对于波形差异较大的spike分类效果较好，但是对于波形比较接近的spike则不甚理想；此外，主成分分析(principal component analysis，PCA)[3-4]、小波变换[5-6]等特征提取方法应用也比较广泛，虽然这些方法提高了特征的分类性能，但是PCA难以完整刻画出spike波形，而且小波变换对小波基的选择并没有有效的准则。

此外，特征聚类也是spike分类中的关键步骤，目前常用的方法有k均值聚类[7]、超顺磁聚类[8]等，虽然这些方法都取得了较好的聚类效果，但是k均值需要首先根据初始聚类中心确定一个初始划分，而且这个初始聚类中心对聚类结果有很大影响；超顺磁聚类虽然是无监督聚类方法，但计算繁琐、速度较慢。封洲燕等利用PCA结合最大最小距离聚类的spike分类方法，在大鼠海马区spike信号的分类中取得了较好的分类效果[9]。但是这种方法只适用于多通道的spike分类。

针对以上问题，本研究提出一种新的spike分类方法，即首先计算spike波形变化率，并基于spike的偶极子模型从理论上探讨了波形变化率在描述spike特征时的优势，然后利用最大差异方法获得spike的低维特征，最后采用高斯混合模型实现特征聚类。波形变化率，即一阶导数，能够有效度量不同神经元spike波形之间的差异，而最大差异算法是一种自适应的特征提取方法，可以根据spike波形自动寻找到差异最显著的特征。因此，本研究提出的spike分类方法可以根据神经信号的不同自适应的提取出具有显著差异的spike波形特征，提高了spike的分类性能。实验中利用仿真数据和大鼠初级视觉皮层(又称V1区)和恒河猴V1区神经信号对算法进行了验证。

1 材料与方法

1.1 锋电位分类方法

假设一次实验(即trial)中，对于给定通道，微电极共记录到了N个spike，分别来自于C个神经元，而且每个spike有M个采样点组成，即Xi={xi,1,xi,2,…,xi,M}(i=1,2,…,N)，则这N个spike可以表示为

(1)

式中，Z为N×M矩阵，表示微电极阵列在一次trial中记录到的所有spike波形的幅值。

Spike分类就是利用模式识别方法将这些无标签的spike信号分为不同类别，以实现对单个神经元活动特性进行研究的目的。Spike分类过程如图1所示。

图1 Spike分类过程Fig.1 Spike sorting procedure

1.1.1 锋电位特征提取

特征提取是spike分类中的关键步骤，特征提取的质量直接关系到分类的性能。从理论上讲，同一神经元发放的锋电位波形相同，而不同神经元的锋电位在波形上存在一定差异，然而，在信号采集过程中，背景噪声模糊了这种差异。变化率，又称陡度[7]，表示幅值随时间变化的改变程度，可以表征波形变化的细微差别，是波的一个重要特征。

本研究使用spike变化率特征的灵感最初是来自于spike的偶极子模型[7]，偶极子p在距偶极子中心r处产生的电势可表示为

(2)

式中，p为偶极子算子，r为电极与神经元之间的距离，θ为向量p与向量r之间的夹角，ε0为电介质常数。

偶极子是由细胞外的电流形成的，该电流是由Na+从细胞外空间流向细胞内空间，以平衡细胞膜而形成的。

从式(2)可以看出，距离神经元远近不同的两个电极，假如第1个电极与神经元间的距离小于第2个电极与神经元间的距离。在这种情况下，从这两个电极记录到的spike会表现出相同的形状但幅值不同。这是因为spike幅值反比例于r2，由于两个记录到的spike具有不同的幅值，所以spike幅值可以作为区分两个不同神经元spike的特征。而变化率是波形的一阶导数，刻画的是波形在不同时刻的波形变化趋势，能明显反映出幅值变化急剧程度，是波形变化的显著数字特征。因此，利用spike波形的变化率作为分类特征，并利用最大差异法[10]对特征进行降维。

(3)

式中，i=1,2,…,M-1，Zk,i表示矩阵Z中的第k行、第i列的元素值，Δt为采样间隔。

(4)

式中，Ld为局部差异向量。

1.1.2 高斯混合模型分类算法

假设spike数据集X={x1,x2,…,xN}服从由K个高斯成分(即K类)组成的高斯混合模型(gaussianmixturemodel，GMM)。对于单个spike样本xi，其高斯混合分布的概率密度函数为

(5)

(6)

GMM的训练过程需要利用最大期望(expectationmaximization，EM)算法进行非线性概率函数的优化，首先对确定的分类数目进行模型初始化，并给出θk的初始估计值θ0k。待求出参数λ=(πk,θk)后，就可以得到每个spike属于每一类的概率，根据最大后验概率准则，将该spike判为概率最大的那一类。EM算法的计算过程如下：

EM算法有两步，即期望歩(E-step)和最大值歩(M-step)，通过更新参数πk，μk，σk在E步和M步之间进行迭代，使似然函数达到最大。

1)E-step：通过似然函数计算当前估计和上次估计的差值Q(p,pold)[5]，表示为

(7)

式中，N和K分别表示spike总数和混合模型中高斯成分的个数。

2)M-step：使式(7)中的Q(p,pold)达到最大，得到新的参数πk，new、μk，new、σk，new，更新过程可由下列式子得出

(8)

这些新的参数可以在又一次的迭代中得到估计和修正，直到使Q(p,pold)达到预定的收敛条件，至此就可以获得参数λ，完成spike的分类。

1.2 评价指标

1.2.1 误分率

对spike分类而言，由于分类而造成的误分样本的个数是一个重要的评价指标。因此，使用误分率来定量衡量分类算法的性能。假设待分数据集X={x1,x2,…,xN}可分为K类，每类的误分样本数为wi(i=1,…,K)，则误分率R可表示为[11]

(9)

1.2.2J3准则值

对于spike分类而言，从模式识别的角度看，提取的特征应当满足两个条件：一是要使每一类的特征值紧密的分布在某个值附近，即类内方差要小；二是不同类之间的特征值分布的距离要尽可能远，即类间距离要大。由类可分性准则可知，特征的类可分性越好，其J3准则值就会越大。J3准则表征了特征的类可分性，定义为[12]

J3=tr{S-1Sm}

(10)

1.3 数据采集

为了验证所提出方法的有效性和实用性，采用仿真数据研究了该算法的可行性和分类精度，用实测数据验证了实际分类效果，并与多种分类算法进行了比较。关于仿真数据和实测数据的来源分别简述如下：

为了说明该算法的有效性，仿真数据选用了公开的spike分类测试数据，来源于文献[13]。该数据共包含有4组仿真信号，每组信号中由噪声水平分别为0.05、0.10、0.15、0.20的4段数据组成, 噪声水平定义为信号背景噪声的标准差。这4组数据分别记为data1、data2、data3和data4。每段数据时间长度为60 s，采样频率为24 kHz，共包含有来自3个神经元发放的大约3 400个spike，每个spike由64个采样点组成。

为了验证该算法的实用性，采用的实测数据包含两部分，实测数据1为从CRCNS.org神经数据共享平台—恒河猴V1区采集得到，选择了其中5组典型的数据，分别记为data5、data6、data7、data8和data9；实测数据2为本课题组从大鼠V1区采集得到，选用其中5组来自不同大鼠且具有代表性的数据，分别记为data10、data11、data12、data13和data14。

实测数据1：来源于Collaborative Research in Computational Neuroscience-Data sharing(CRCNS)的数据共享平台[14]。实验动物为体重为4～5 kg的恒河猴1只，利用氯胺酮麻醉后在V1区植入8×8微电极阵列(Neuronexus，电极间距为200 μm，电极直径30 μm)采集得到，详细实验过程请参考文献[15]。所选用的5组数据分别包含有32 042、54 749、41 097、31 151和28 116个spike，采样频率为24.4 kHz，每个spike由12个采样点组成。

实测数据2：实验动物为体重200～250 g的成年Long Evans(LE)大鼠5只，雌雄不拘。利用10%水合氯醛麻醉后在V1区植入2×8微电极阵列(Microprobe，铂铱合金，电极间距250 μm，电极直径125 μm，尖端直径15 μm，电极阻抗在0.5～1.0 MΩ之间)通过数据采集系统(CerberusTM，Blackrock Inc.)采集得到，详细实验过程请参考文献[16]。所选用的5组数据分别包含有747、1 329、810、1 130和1 417个spike，采样频率为30 kHz，每个spike由44个采样点组成。

2 结果

图2 3个典型的spike模板及其变化率。(a)～(c)3个典型的spike模板波形；(d)～(f)对应的变化率Fig.2 Three spike templates and its waveform changing rate. (a)～(c) Waveforms of the three spike templates；(d)～(f) Waveforms changing rate of the three spike templates

图3 3种不同方法对相同数据特征提取的统计分布对比。(a)波形变化率最大差异法；(b)PCA方法；(c)原始波形最大差异法Fig.3 Statistical distribution of features based on three extraction methods for the same data. (a) The maximum-difference of waveform changing rate method; (b) The PCA method; (c) The maximum-difference of original waveform method

图2为3个不同的spike模板波形图及其变化率。由图可知，3个spike模板的变化率差异要比原始信号的波形差异更显著。图3为波形变化率最大差异法、PCA法和原始波形最大差异法3种算法提取的第一维特征值统计分布，其中的粗实线为高斯曲线拟合结果。由图可知，除PCA法呈单峰分布外，本方法和原始波形最大差异法所提取特征的分布均呈双峰形状，但本方法提取的特征两峰之间距离较大，而且没有重叠。由此可知本方法提取的特征要优于PCA和原始波形最大差异特征提取方法。

2.1 仿真结果

图4为其中一组仿真数据的聚类结果。图中(a)是4个不同噪声水平(分别是0.05、0.10、0.15、0.20)的仿真数据波形，从中可以看出，随着噪声水平的增加，三类spike之间的差异越来越模糊；(b)～(e)分别为4种不同聚类效果方法的结果，即变化率特征的高斯混合模型聚类(变化率特征+GMM)、PCA特征的高斯混合模型聚类(PCA+GMM)、幅值特征的高斯混合模型聚类(幅值特征+GMM)、变化率特征的k均值聚类(变化率特征+k均值)。由图可知，随着噪声水平的增加，4种分类方法中不同spike类之间的重叠程度都逐渐增加，差异度变小，但是与其他3种方法相比，本方法类间距变化较小，依然保持着较好的分类效果，有着良好的分类性能。

为了进一步度量本算法的分类性能，表1给出了4种不同分类方法对4个仿真数据集的误分率对比结果。从表中可以看出，随着噪声水平的增加，4种方法的误分率都呈逐渐升高趋势，但与其他3种方法相比，在不同噪声水平时本方法的误分率都是最低的，分别为1.18%、1.41%、2.27%和2.98%。与图4的分类结果一致。综合图4和表1的结果可知，从特征提取的角度看，与PCA特征提取方法相比，最大差异特征提取方法能够有效选择出差异最显著的特征，而且与原始波形相比，变化率受噪声的影响相对较小，具有一定的抗噪能力；从聚类的角度看，GMM算法对spike波形特征的非高斯分布可以进行有效拟合，聚类效果也优于经典的k均值算法。

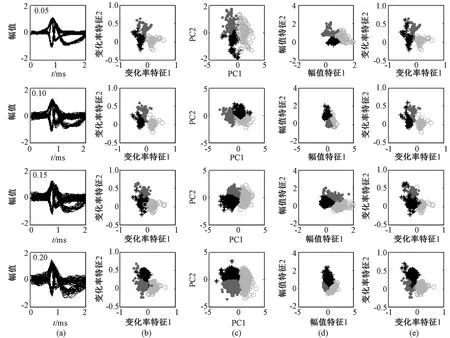
图4 不同特征提取方法分类结果对比(图中的不同颜色代表不同类别的锋电位特征值分布，最左侧图中数字表示噪声水平)。(a)Spike波形；(b)变化率特征+GMM算法；(c)PCA+GMM算法；(d)幅值特征+GMM算法；(e)变化率特征+k均值算法Fig.4 Results for different spike sorting methods from simulated data(The different colors denote the features of spike from the different clusters and the number in left figures denote noise level). (a) Spike waveforms; (b) Spike sorting method based on changing rate features and GMM cluster; (c) Spike sorting method based on PCA features and GMM cluster; (d) Spike sorting method based on waveform features and GMM cluster; (e) Spike sorting method based on waveform changing rate features and k-means cluster

表1 仿真数据的不同方法误分率对比表Tab.1 Comparison of misclassification rate of different methods in simulated data

注：平均误分率用(均值±标准差)表示(n=4)；*表示P<0.05，**表示P<0.01。

Note: The average misclassification rate is presented by mean ± standard deviation (n=4),*denotesP<0.05 and**denotesP<0.01.

2.2 实测结果

实测数据的分类结果如图5所示，其中前两组数据(data5和data6)来自于恒河猴V1区，后两组数据(data10和data11)来自于大鼠V1区。图中(a)是实测数据的spike波形；(b)为本方法的分类结果，(c)～(e)是其他3种不同方法的分类结果，与仿真数据的分类方法一致。从图(b)和(e)可以看出，当特征提取方法相同时，分类结果相似，方框标出了两种方法的分类结果不同之处。但是，从分类结果来看，本方法的聚类结果要明显好于其他方法，类间距离明显，类与类之间没有重叠，与仿真数据的结果一致。

图5 实测数据分类结果对比(图中的不同颜色代表不同类别的锋电位特征值分布)。(a)Spike波形；(b)变化率特征+GMM算法；(c)PCA+GMM算法；(d)幅值特征+GMM算法；(e)变化率特征+k均值算法Fig.5 Results for different spike sorting methods from real data (The different colors denote the features of spike from the different clusters). (a) Spike waveforms; (b) Spike sorting method based on changing rate features and GMM cluster; (c) Spike sorting method based on PCA features and GMM cluster; (d) Spike sorting method based on amplitude features and GMM cluster; (e) Spike sorting method based on changing rate features and k-means cluster

由于实测数据中每个spike信号的类别是未知的，难以用上述的误分率进行衡量，为了能定量度量本算法在实测数据中的分类性能，此处选择类可分性度量指标，J3准则值，对上述分类算法进行定量评估。表2给出了实测数据1和实测数据2的分类J3准则值。恒河猴的数据结果显示(实测数据1)，本算法的类可分性显著优于幅值特征+GMM算法(P<0.05)。虽然与PCA+GMM和变化率特征+k均值算法相比，并没有显著统计学差异，但是在平均水平上，本算法J3准则值高于这两种算法；大鼠的数据结果显示(实测数据2)，本算法显著优于PCA+GMM(P<0.05)和幅值特征+GMM(P<0.01)，而且平均J3准则值也高于变化率特征+k均值算法。综上可知，无论是恒河猴数据还是大鼠数据，本算法的平均J3准则值都大于其他3种算法，表现出了较好的类可分性。

表2 实测数据不同方法的J3准则值对比表Tab.2 Comparison of J3 criterion values of different methods in real data

注：J3平均值用(均值±标准差)表示(n=5)；*表示与本算法相比P<0.05，**表示与本算法相比P<0.01。

Note: The averageJ3value is presented by mean ± standard deviation (n=5),*denotesP<0.05 compared with the proposed algorithm,**denotesP<0.01 compared with the proposed algorithm.

3 讨论

Spike分类被认为是解析大脑信息处理机制的第1步[17]。Spike的产生机制决定了波形变化对于spike分类的重要性，而偶极子模型描述了影响spike波形变化的因子。本研究针对波形特征给出了一种新的spike分类方法，即首先提取出spike波形的变化率特征，然后利用最大差异法对波形变化率特征进行降维，最后利用高斯混合模型聚类算法对特征进行聚类，实现spike分类。算法验证方面采用来自公开的spike分类仿真测试数据和来自不同动物种类V1区的实测数据，保证了实验结果的客观性和通用性。

特征提取和聚类对于spike分类而言是两个至关重要的步骤。在特征提取上，通过前期大量的实验数据分析，本研究提出了一种新的spike分类特征提取方法，即基于spike的波形变化率，利用最大差异算法获得差异最显著的spike分类特征。本研究提出的spike分类特征提取方法最大的优势在于其是一种自适应的特征提取方法，可以根据spike波形自适应的提取出差异最显著的特征，而且对于spike波形相近的神经元，也具有较好的分类效果。在聚类上，由于神经元活动的复杂性和非平稳性，以及特征选择的自适应性，在spike特征分布上往往表现出非高斯特性，因此，选用GMM算法对上述spike分类特征进行聚类，GMM分类算法是一种统计聚类方法，可以有效表征spike特征的非高斯分布。

在实验分析上，本研究选用了公开的spike分类仿真数据和多种实测数据，并与目前常用的spike分类算法进行了对比。由仿真数据结果可知，本方法的平均误分率相对较低，对于不同的噪声水平，即0.05、0.10、0.15、0.20，其spike误分率分别为1.18%±1.18%、1.41%±1.06%、2.27%±1.51%、2.98%±2.06%(见表1)，表明本算法具有较高的分类精度；从对实测数据结果来看，本方法的平均J3准则值是4种方法中最大的，恒河猴数据为13.50±5.26，大鼠数据为26.43±10.46(如表2)，说明本算法得到的结果具有最大类可分性。仿真和实测数据的结果具有一致性，表明了所提出方法的有效性。

综上可知，不论从特征提取的角度，还是从聚类的角度，本方法都体现了较好的分类性能。波形变化率能够有效度量不同神经元spike波形之间的差异，GMM算法对spike波形特征的非高斯分布可以进行有效拟合，聚类效果也优于经典的聚类算法。但是，也不可否认的是，与原始波形相比，波形变化率可能会放大噪声，不过在嵌入式高放大倍数的spike信号采集方式下，加之特征提取前spike经过了滤波、阈值检测、波形对齐等步骤进行预处理，已将噪声干扰减小到最小，信噪比相对较高，故一般来说这个问题对spike分类而言影响较小。

4 结论

本研究提出了一种基于波形变化率特征和高斯混合模型聚类的spike分类方法，即首先提取出spike波形的变化率特征，然后利用最大差异法对波形变化率特征进行降维，最后利用高斯混合模型聚类算法对特征进行聚类，实现spike分类。并利用仿真信号和来自大鼠V1区及恒河猴V1区神经信号进行了验证。仿真和实测数据结果表明，本方法不仅可以自适应提取出具有显著差异的spike特征，而且具有较高的分类精度和较好的类可分性，为基于spike信号的神经信息编码和解码研究奠定了基础。

[1] Lewicki MS. A review of methods for spike sorting: the detection and classification of neural action potentials [J]. Network: Comp Neural, 1998, 9(4): R53-R78.

[2] Kim KH, Kim SJ. Neural spike sorting under nearly 0-dB signal-to-noise ratio using nonlinear energy operator and artificial neural-network classifier [J]. IEEE Trans Biomed Eng, 2000, 47(10): 1406-1411.

[3] Adamos DA, Kosmidis EK, Theophilidis G. Performance evaluation of PCA-based spike sorting algorithms [J]. Comput Meth Prog Bio, 2008, 91(3): 232-244.

[4] 丁伟东，袁景淇，梁培基. 多电极锋电位信号检测与分类方法研究 [J]. 仪器仪表学报, 2006, 27(12): 1636-1640.

[5] Bestel R, Daus AW, Thielemann C. A novel automated spike sorting algorithm with adaptable feature extraction [J]. J Neurosci Methods, 2012, 211(1): 168-178.

[6] 丁颖，范影乐，杨勇. 基于小波特征与动态高斯混合模型的动作电位分类研究 [J]. 仪器仪表学报, 2011, 32(2): 475-480.

[7] Paraskevopoulou SE, Barsakcioglu DY. Feature extraction using first and second derivative extrema (FSDE) for real-time and hardware-efficient spike sorting [J]. J Neurosci Methods, 2013, 215(1): 29-37.

[8] Wild J, Prekopcsak Z. Performance comparison of extracellular spike sorting algorithms for single-channel recordings [J]. J Neurosci Methods, 2012, 203(2): 369-376.

[9] 王静，封洲燕. 多通道神经元锋电位检测和分类的新方法 [J]. 生物化学与生物物理进展, 2009, 36(5): 641-647.

[10] Gibson S, Judy JW. Technology-aware algorithm design for neural spike detection, feature extraction, and dimensionality reduction [J]. IEEE Trans Neur Sys Reh, 2010, 18(5): 469-478.

[11] Geng Xinling, Hu Guangshu. Unsupervised feature selection by kernel density estimation in wavelet-based spike sorting [J]. Biomed Signal Proces, 2012, 7(2): 112-117.

[12] Theodoridis S, Koutroumbas K, 著. 李晶皎, 王爱侠, 王骄，等译. 模式识别 [M]. 北京: 电子工业出版社, 2010: 188-190.

[13] Martinez J, Pedreira C, Ison MJ, et al. Realistic simulation of extracellular recordings [J]. J Neurosci Methods, 2009, 184(2): 285-293.

[14] Chu CCJ, Chien PF, Hung CP. Multi-electrode recordings of ongoing activity and responses to parametric stimuli in macaque V1 [DB/OL]. CRCNS.org, http://dx.doi.org/10.6080/K0J1012K, 2014-03-06/2014- 10-10.

[15] Chu CCJ, Chien PF, Hung CP. Tuning dissimilarity explains short distance decline of spontaneous spike correlation in macaque V1 [J]. Vision Res, 2014, 96(1): 113-132.

[16] 万红，张晓娜，刘新玉，等. 基于局部场电位固有模态分量的响应调谐特性研究 [J]. 中国生物医学工程学报, 2013, 32(3): 292-298.

[17] Gibson S, Judy JW, Markovic D. Spike sorting: the first step in decoding the brain [J]. IEEE Signal Proc Mag, 2012, 29(1): 124-14.

Spike Sorting Using Gaussian Mixture Model of Waveform Feature

Wan Hong*Zhang Chao Liu Xinyu Shang Zhigang

(SchoolofElectricalEngineering,ZhengzhouUniversity,Zhengzhou450001,China)

Spike sorting is one of basic steps to study brain information processing mechanism. Regarding to the complexity and non-stationary of spike signals, a new spike sorting method based on waveform changing rate features and Gaussian mixture model (GMM) cluster was proposed in this work, in which the GMM described the probability density function of spike features from statistical clustering viewpoint. In the proposed method, firstly, the changing rate of spike waveforms was calculated, then low-dimensional features were obtained using maximum-difference method, and the features were finally sorted by the GMM. The accuracy and feasibility of the algorithm was measured by the simulated data from the published database, and the practicality was validated by the real data from primary visual cortex of five rats and one macaque monkey. And its performance was compared to other three sorting methods that based on principal component features and GMM cluster, based on waveform features and GMM cluster as well as based on waveform changing rate features andk-meancluster. For the simulated data, the misclassification rate of proposed method below the other three methods, that is 1.18%±1.18%, 1.41%±1.06%, 2.27%±1.51% and 2.98%±2.06% when the noise level is 0.05, 0.10, 0.15 and 0.20, respectively. For the real data, theJ3value of proposed method is 13.50±5.26 with monkey data and 13.50±5.26 with rat data. Compared with the other three methods, the proposed method gives the maximumJ3value and is higher significantly than the sorting method based on waveform features and GMM cluster. It has higher precision and classification performance as well as provides an effective approach to achieve reliable spike sorting.

spike sorting; waveform changing rate; maximum-difference algorithm; gaussian mixture model

10.3969/j.issn.0258-8021. 2016. 04.003

2014-10-28， 录用日期:2016-05-10

国家自然科学基金(U1304602)；河南省重点科技攻关项目(122102210102, 162102310167)

R318.04

A

0258-8021(2016) 04-0402-09

*通信作者(Corresponding author)， E-mail: wanhong@zzu.edu.cn