再入点参数偏差对过载定延时引信误差研究*
余江波,郑健,王伟,何雨洋
(火箭军工程大学 a.一系; b. 初级指挥学院,陕西 西安 710025)
探测跟踪技术
再入点参数偏差对过载定延时引信误差研究*
余江波a,郑健a,王伟b,何雨洋a
(火箭军工程大学 a.一系; b. 初级指挥学院,陕西 西安 710025)
为分析导弹再入点速度偏差和弹道倾角偏差对过载定延时引信爆高精度的影响,针对再入段的飞行特性,通过再入段弹道模型,分别分析实际弹道再入点速度、弹道倾角与标准弹道的偏差对过载定延时引信爆高精度的影响,仿真结果表明:弹道倾角偏差对过载定延时引信爆高精度影响较大,在实际飞行过程中传送再入点速度和弹道倾角时可有效减小过载定延时引信爆高误差。
弹道导弹;再入段;过载;引信;精度;误差
0 引言
过载定延时引信由过载信号器和延时电路组成,发射前根据标准弹道装订预定过载时对应高度到预定爆高的延时时间,弹头再入后在预定过载时过载开关动作,延时电路开始延时,延时结束时给出引爆信号。该引信简单可靠,且不受电磁干扰,但爆高精度较差。
由于实际弹道与标准弹道存在偏差[1],发射前装订的延时量与实际所需的延时量有误差,导致弹头实际爆高与装订爆高存在误差,因而影响了作战效果。本文主要分析了实际弹道再入点速度、弹道倾角与标准弹道再入点速度、弹道倾角的偏差对过载定延时引信爆高精度的影响,提出了在实际飞行过程中传送再入点速度、弹道倾角条件下可有效减小过载定延时引信爆高误差。
1 再入段弹道仿真分析
弹道导弹的再入段是指弹头重新进入稠密大气层的一段弹道,即再入点开始到弹头引爆的这段弹道[1-2]。
1.1 再入段弹道模型基本假设
弹头在再入段主要受地球引力和大气阻力的作用,由于再入段弹头速度快(一般为几km/s)、飞行时间较短(一般为几十s),所以在研究再入段弹道时,可作以下假设[1-3]:
(1) 飞行时间较短,可不考虑地球旋转,即ω=0。
(2) 认为地球为圆球,不考虑地球扁率影响,即地球引力场为一有心力场。
(3) 认为弹头纵对称轴一直处于由弹头再入点的速度矢量ve和径向re组成的二维平面内,即侧滑角β=0。
在以上基本假设条件下,导弹在再入段运动时可不受垂直于射面的侧力作用,因此再入段运动可理解为一平面运动[3]。
1.2 再入段弹道模型描述
导弹自由段是在近似真空环境中飞行,可理解为不受空气影响,因而可理解为其弹道为椭圆弹道[4]。弹头再入段在稠密的大气中飞行,且弹头速度非常快,空气对弹道的影响不可忽略。由于弹道导弹再入段的高度h为0~70 km范围,随着弹头所处的几何高度h不同,对应的温度T、压强p、密度ρ、重力加速度g、声速a随着h变化,根据参考文献[5-7]的标准大气模型可得到0~70 km任意高度所对应的T,p,ρ,g,a。
根据弹头受力分析得到弹头再入段运动微分方程组为[8-11]
(1)
式中:m为弹头质量;v为弹头的速度;Θ为弹道倾角;R为地球平均半径,取6 371 km;h为导弹与地面的高度;r=R+h为导弹与地心的距离;L=Rf为导弹再入段任意位置时的射程;X为阻力,Y为升力。其中X计算公式如下:
(2)
一般情况下导弹弹头以任意姿态进入大气层,由于弹头是静稳定的,因此,当有冲角再入大气时,稳定力矩将使其减小,甚至为0。所以在研究弹头的质心运动时,可认为冲角α=0,即可认为导弹在再入段不受升力的作用[1,3]。此时,弹头再入段运动微分方程组可由式(1)导出,即
(3)
给出弹头再入点的速度vc、地心距rc、弹道倾角Θc,并结合弹头质量m、阻力X以及标准大气参数可根据上述运动微分方程组求解弹头再入段弹道。
1.3 再入段弹道模型仿真分析
根据参考文献[12],导弹关机点参数为:关机点速度vK为2 543.2 m/s,弹道倾角ΘK为35°,地心距rK为6 450 km。根据导弹自由段椭圆弹道模型[8],假设再入点高度为70 km,得到导弹再入点参数为:再入点速度vc为2 577.5 m/s,弹道倾角Θc为-35.961 8°,地心距rc为6 440.9 km。
令导弹再入点时刻为0时刻,根据导弹再入段模型和导弹再入点参数vc,Θc和rc可解出任意时刻t时弹头的参数v(t),h(t),Nx(t),Θ(t),弹头再入段仿真结果如图1所示。
仿真得到弹道导弹再入段v(t),h(t),Nx(t),Θ(t)如图1所示。再入段时间为43.299 s。再入段速度如图1a)所示,再入点速度为2 577.5 m/s,由于弹头刚进入大气时,大气密度小,所受空气阻力小,此时地球引力大于空气阻力,速度仍在增加,在24 s左右达到最大速度2.7 km/s,在落地点达到最小速度1.4 km/s。再入段高度如图1b)所示, 弹头高度由70 km不断减小。再入段过载如图1c)所示,在再入段前期,弹头速度快,但大气密度很小,此时弹头所受气阻力很小,因而过载值很小;随着弹头高度的减小,弹头速度有所减小,但大气密度快速增大,此时负向过载迅速增大,在39.5 s左右负向过载达到最大约为-13.5;由于负向过载的增加,此时弹头速度迅速减小,大气密度增大对过载的影响小于速度迅速减小的影响,此时负向过载逐渐减小[13]。再入段弹道倾角如图1d)所示,弹道倾角单调递减,由再入点-35.961 8°变化到43.299 s时的-46.1°。
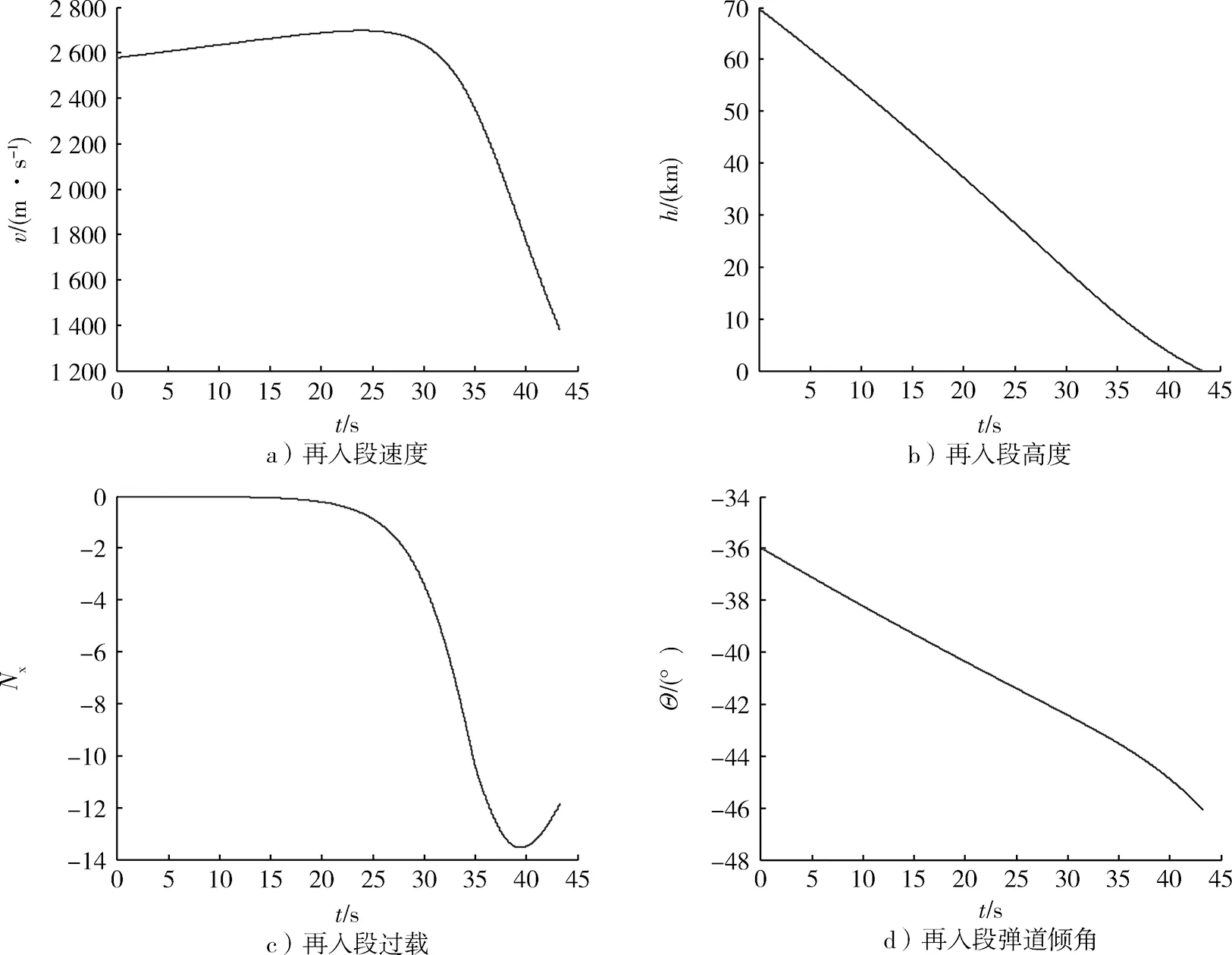
图1 弹道导弹再入段仿真结果图Fig.1 Reentry segment’s simulation results of ballistic missile
2 再入点参数偏差对过载定延时误差分析
假设弹头再入点参数为:速度vc为2 577.5 m/s,弹道倾角Θc为-35.9618°,地心距rc为6 440.9 km,再入点时刻为0时刻。利用再入段弹道模型,仿真得到标准再入弹道参数(Nx-h-t)如图2所示。
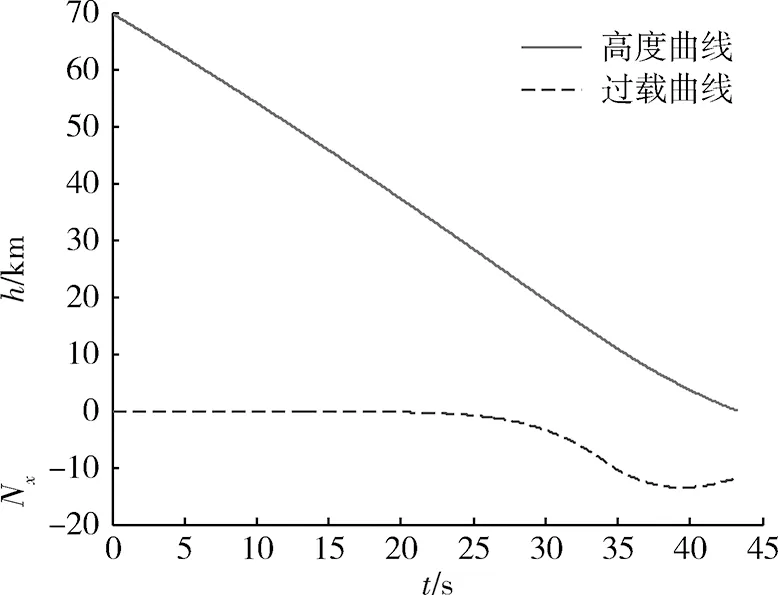
图2 标准再入弹道参数图Fig.2 Standard reentry segment’s parameters
由图2可见再入段高度单调递减,前期过载值单调递减,当过载达到负过载开关预定阈值时,此时对应某一高度和时刻,该时刻到预订爆高对应时刻的延时时间为Δt。发射前根据计算的标准再入弹道和要求爆高得到过载定延时引信延时时间Δt。弹头实际再入后,当再入轴向过载值达到负过载开关预定阈值(假设过载为-10)时,负过载开关动作,过载定延时引信开始延时。当装订的延时时间Δt结束时,过载定延时引信给出引爆信号。
在34.759 s时刻,过载值达到负过载开关预定阈值(过载为-10),此时弹头高度为11.312 km。以100 m为爆高间隔,选取可能作为弹头爆高的高度范围,根据标准再入弹道得到每个爆高h对应的过载定延时引信延时时间Δt如表1所示。
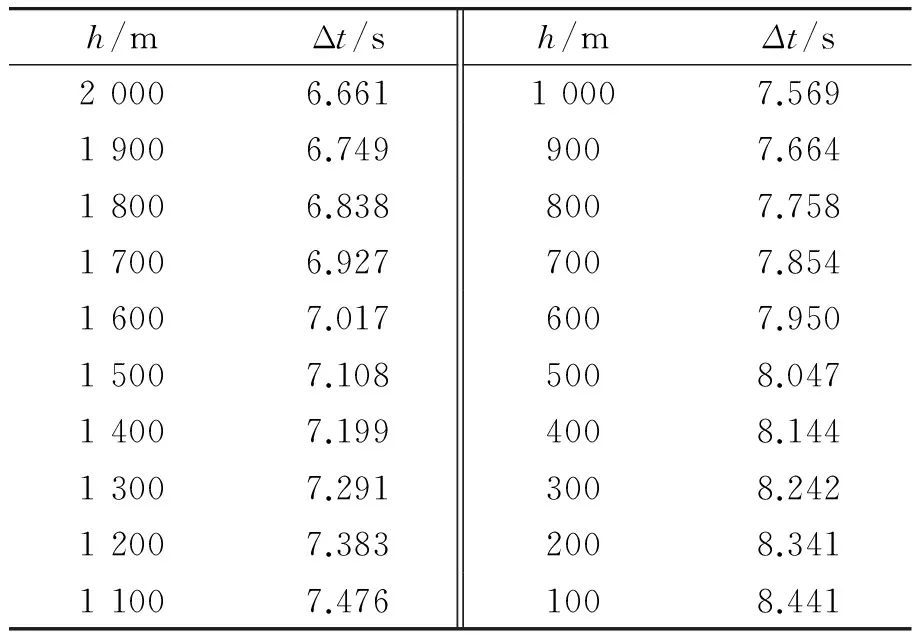
表1 过载定延时引信延时时间表Table 1 Delay time schedule of overload delay fuze
理论上,发射前装订时可选低于11.312 km高度(过载为-10)的任意高度作为弹头的爆高,得到不同爆高对应的定延时时间Δt。由于气象、导弹控制系统误差等导致弹头实际再入点参数与标准弹道再入点参数存在一定的偏差,导致弹头实际爆高与预订爆高存在误差,影响其杀伤效果[14-15]。
2.1 再入点速度偏差对爆高误差分析
假设发射前装订爆高为1 000 m,由表1可得过载定延时引信延时时间为7.569 s,假设实际飞行弹道再入点速度与标准弹道再入点速度的偏差范围为±20 m/s,实际飞行的再入点弹道倾角与标准弹道的弹道倾角无偏差,此时实际爆高如图3所示。
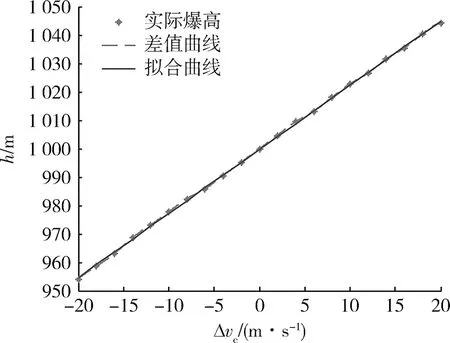
图3 存在再入点速度偏差条件下的爆高Fig.3 Blast height on the condition of reentry point’s velocity error
仿真得到存在再入点速度偏差条件下的实际爆高如图3所示。最大爆高为1 044.3 m,最小爆高为954.1 m,均值为999.8 m,标准差为28.0 m,爆高误差最大为-45.9 m。将爆高h和再入点速度偏差Δvc线性拟合得
h=999.8+2.258 3Δvc.
2.2 再入点弹道倾角偏差对爆高误差分析
假设实际飞行弹道再入点弹道倾角与标准弹道再入点弹道倾角的偏差范围为±1°,实际飞行的再入点速度与标准弹道的再入点速度无偏差,此时实际爆高如图4所示。
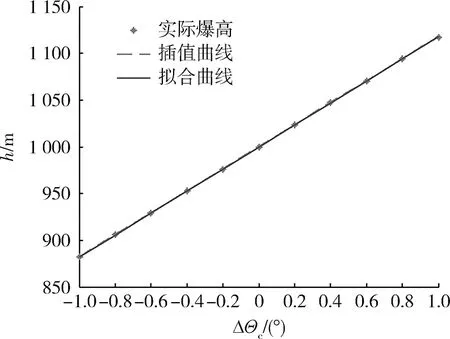
图4 存在再入点弹道倾角偏差条件下的爆高Fig.4 Blast height on the condition of reentry point’s flight path angle error
仿真得到存在再入点弹道倾角偏差条件下的实际爆高如图4所示。最大爆高为1 117.1 m,最小爆高为881.8 m,均值为999.7 m,标准差为78.1 m,爆高误差最大为-118.2 m。将爆高h和再入点速度偏差ΔΘc线性拟合得
h=999.7+117.674 3ΔΘc.
2.3 再入点速度和弹道倾角偏差对爆高误差分析
假设实际飞行弹道再入点速度与标准弹道再入点速度的偏差范围为±20 m/s,实际飞行弹道再入点弹道倾角与标准弹道再入点弹道倾角的偏差范围为±1°,此时实际爆高如图5所示。

图5 存在速度和弹道倾角偏差条件下的爆高Fig.5 Blast height on the condition of reentry point’s velocity and flight path angle deviation
仿真得到存在再入点速度和弹道倾角偏差条件下的实际爆高如图5所示。最大爆高为1 163.7 m,最小爆高为838.1 m,均值为999.5 m,标准差为83.3 m,爆高误差最大为163.7 m。由图6可以看出再入点弹道倾角偏差比再入点速度偏差对过载定延时引信爆高精度影响大。将爆高h和Δvc和ΔΘc线性拟合得
h=999.4+2.252 2Δvc+117.655 3ΔΘc.
由于存在再入点速度和弹道倾角偏差条件下的实际爆高精度较差,可利用测得的加速度信息实时改变延时时间的方法或者在实际飞行过程中传送再入点速度vc和弹道倾角Θc的方法,本文对第1种方法不作具体分析。
3 传送vc和Θc条件下爆高误差分析
由第2章分析可得,由于实际弹道存在关机点速度偏差Δvc和弹道倾角偏差ΔΘc,导致过载定延时引信按发射前装订的延时时间Δt延时带来较大的爆高误差,影响其杀伤效果。假设当在实际的飞行过程中能传送再入点速度vc和弹道倾角Θc时,可快速计算一条实际的再入段弹道,根据该实际再入段弹道计算过载定延时引信延时时间Δt′,能有效减小实际爆高误差。例如在实际的飞行过程中传送的再入点速度vc比标准弹道大10 m/s,传送的再入点弹道倾角Θc比标准弹道大0.5°时,利用再入段弹道模型,得到标准再入弹道参数和实际再入弹道参数(Nx-h-t)对比如图6所示。

图6 实际再入弹道和标准再入弹道参数对比图Fig.6 Actual reentry trajectory and standard reentry trajectory parameters comparison chart
在标准弹道中,34.759 s时刻过载值达到负过载开关预定阈值-10,此时弹头高度为11.312 km,当爆高为1 000 m时,延时时间为7.569 s。在实际弹道中,34.964 s时刻过载值达到负过载开关预定阈值-10,此时弹头高度为11.346 km,当爆高为1 000 m时,延时时间为7.646 s。实际飞行时,过载定延时引信7.569 s延时爆高为1 081.2 m,过载定延时引信7.646 s延时爆高为999.6 m,可见在飞行过程中传送再入点速度vc和弹道倾角Θc时可有效减小过载定延时引信误差。
4 结束语
本文对再入点速度偏差和弹道倾角偏差对过载定延时引信爆高精度进行了研究。首先通过建立弹道导弹再入段弹道模型,仿真得到再入段的弹道参数(Nx-h-t),分别对再入点速度偏差Δvc和弹道倾角偏差ΔΘc对过载定延时引信爆高精度的影响进行了分析,仿真结果表明再入点弹道倾角偏差ΔΘc比再入点速度偏差Δvc对过载定延时引信爆高精度影响大,在实际的飞行过程中传送再入点速度vc和弹道倾角Θc条件下可有效减小过载定延时引信误差。
[1] 张毅,肖龙旭,王顺宏. 弹道导弹弹道学[M].长沙:国防科技大学出版社,2005:243-250. ZHANG Yi, XIAO Long-xu, WANG Shun-hong. The Trajectory of Ballistic Missile[M]. Changsha: National University of Defense Technology Press, 2005:243-250.
[2] 祝强军. 弹道导弹弹道仿真与优化设计[D].西安:西北工业大学,2007:15-18. ZHU Qiang-jun. Trajectory Simulation and Optimization of the Ballistic Missile[D]. Xi’an: Northwestern Polytechnical University, 2007:15-18.
[3] 祝庆国,刘刚,鲜勇. 战术弹道导弹再入段机动弹道仿真研究[J]. 战术导弹技术,2008,10(1):79-82. ZHU Qing-guo, LIU Gang, XIAN Yong. Simulation of Reentry Maneuvering Trajectory of Tactical Ballistic Missile[J]. Tactical Missile Technology, 2008,10(1):79-82.
[4] 侯煜博,沈晓峰,李思思. 战术弹道导弹拦截的仿真研究[J].弹道学报,2007,19(3):34-37. HOU Yu-bo, SHEN Xiao-feng, LI Si-si. Research on Simulation of Tactical Ballistic Missile Interception[J]. Journal of Ballistics, 2007,19(3):34-37.
[5] 高洪月. 弹道导弹的弹道设计与仿真[D].哈尔滨:哈尔滨工业大学,2010:14-17. GAO Hong-yue. Trajectory Simulation and Design of the Ballistic Missile[D]. Harbin: Harbin Insititute of Technology, 2010:14-17.
[6] 杨涛,曹锐,王明海. 弹道导弹再入段大气参数修正[J]. 弹箭与制导学报,2009,29(3):166-168. YANG Tao, CAO Rui, WANG Ming-hai. Atmosphere Parameter Error Correction on Range of Reentry Ballistic Missile[J]. Journal of Projectiles, Rockets, Missiles and Guidance, 2009,29(3):166-168.
[7] 钱山,郑伟,张士峰,等. 一种弹道导弹再入弹道解析方法[J]. 飞行力学,2007,25(4):54-57. QIAN Shan, ZHENG Wei, ZHANG Shi-feng, et al. An Analytic Solution of the Ballistic Missile’s Reentry Trajectory[J]. Flight Dynamics, 2007,25(4):54-57.
[8] 范锐锐,王明海. 遗传算法解算弹道导弹再入段弹道[J]. 弹箭与制导学报,2010,30(5):156-158. FAN Rui-rui, WANG Ming-hai. Solution of Reentry Trajectory of Ballistic Missile Using Genetic Algorithm[J]. Journal of Projectiles, Rockets, Missiles and Guidance, 2010,30(5):156-158.
[9] 李毅,刘晶,邵锡军. 战术弹道导弹弹道仿真建模技术研究[J]. 弹箭与制导学报,2011,31(2):145-148. LI Yi, LIU Jing, SHAO Xi-jun. Research on Modeling Technology for Tactical Ballistic Missile Trajectory Simulation[J]. Journal of Projectiles, Rockets, Missiles and Guidance, 2011,31(2):145-148.
[10] 汤阳春,娄寿春,赵辉. 战术弹道导弹再入段弹道仿真设计[J]. 弹箭与制导学报,2006,26(2):98-99. TANG Yang-chun, LOU Shou-chun, ZHAO Hui. Simulation Design for Reentry of the Trajectory of TBM[J]. Journal of Projectiles, Rockets, Missiles and Guidance, 2006,26(2):98-99.
[11] 苏娟. 导弹防御系统目标速度计算方法研究[J]. 飞行力学,2005,23(4):59-62. SU Juan. On the Computational Method for the Object Velocity of a Missile’s Defense System[J]. Flight Dynamics, 2005,23(4):59-62.
[12] 呼玮,杨建军,龙光正,等. 弹道导弹被动段拦截时间窗口建模与仿真[J].弹箭与制导学报,2010,30(3):181-184. HU Wei, YANG Jian-jun, LONG Guang-zheng, et al. Modeling and Simulation of the TBM Post-Boost Interception Time Window[J]. Journal of Projectiles, Rockets, Missiles and Guidance, 2010, 30(3): 181-184.
[13] 高策,张淑梅,赵立荣,等. 基于数值积分法的弹道导弹落点实时预测[J]. 计算机测量与控制,2012,20(2):404-406. GAO Ce, ZHANG Shu-mei, ZHAO Li-rong, et al. A Real-Time Forecast Method for Impact Point of Ballistic Missile Based on Numerical Methods of Integration[J]. Computer Measurement & Control, 2012,20(2):404-406.
[14] 刘华章,李水杰,江贤志,等. 某型导弹加速度信号源设计[J]. 兵工自动化,2013,32(6):62-65. LIU Hua-zhang, LI Shui-jie, JIANG Xian-zhi, et al. Design of Certain Type Missile Acceleration Signal Source[J]. Ordnance Industry Automation, 2013,32(6):62-65.
[15] 王亚斌,刘明杰,谭惠民. 引信过载随机过程计算机模拟[J]. 机械工程学报,2004,40(5):30-33. WANG Ya-bin, LIU Ming-jie, TAN Hui-min. Computer Simulation for Stochastic Process of Overload in Fuse[J].Journal of Mechanical Engineering, 2004,40(5):30-33.
Error of Overload Setting Time Delay Fuse Caused by Trajectory Parameter Deviations of Reentry Point
YU Jiang-boa,ZHENG Jiana,WANG Weib,HE Yu-yanga
(The Rocket Force Engineering University,a.1st Department;b.Primary Command Academy,Shaanxi Xi’an 710025,China)
For the purpose of analyzing the influence of velocity deviation and flight path angle deviation of the missile's reentry point upon the precision of overload setting time delay fuse height of burst, a model of reentry trajectory is built based on the flight characters of the reentry segment, and the velocity deviation and flight path angle deviation between virtual trajectory and standard trajectory and their influence on the precision of overload setting time delay fuse height of burst are analyzed. The simulation results show that the deviation of flight path angle is more influential on the fuse precision, and in real trajectory flight, the transmission of velocity and flight path angle of the reentry point can effectively reduce the error ofoverload setting time delay fuse height of burst.
ballistic missile; reentry segment; overload; fuse; precision; error
2014-12-30;
2016-02-30
余江波(1989-),男,湖南长沙人。硕士生,主要从事引控与突防研究。
10.3969/j.issn.1009-086x.2016.06.020
TJ761.3;TJ43
A
1009-086X(2016)-06-0115-06
通信地址:710025 陕西西安灞桥洪庆镇同心路2号4502分队
E-mail:827620438@qqq.com

