基于改进SIFT和RANSAC图像拼接算法研究

马 强，项昭保，黄良学，王博化

(重庆邮电大学 工业物联网与网络化控制教育部重点实验室，重庆 400065)

基于改进SIFT和RANSAC图像拼接算法研究

马 强，项昭保，黄良学，王博化

(重庆邮电大学 工业物联网与网络化控制教育部重点实验室，重庆 400065)

就目前图像拼接算法复杂性和RANSAC算法迭代次数多的问题，文中提出了一种新的图像拼接算法。通过提取特征点、图像配准和加权平均融合方法，对图像进行拼接。利用改进算法提取特征点，减少了算法复杂度。此外，改进的RANSAC算法能够用来减少迭代次数。实验结果表明：该方法能够有效减少运算量，加快拼接速度，拼接效果较为理想。

图像拼接；SIFT算法；RANSAC算法；图像融合

0 引 言

近年来，图像拼接技术得到了广泛关注。配准的好坏对图像拼接的质量和效率有很大影响，是图像拼接的关键[1]。目前使用最广泛的特征匹配算法是尺度不变特征变换匹配算法[2](Scale Invariant Feature Transform,SIFT)。但是SIFT提取特征点后，必须排除误匹配点。传统的随机取样一致性算法[3](RANdom SAmple Consensus,RANSAC)迭代次数比较多，运行比较耗时，远远降低了图像拼接算法的效率。

当前主要的图像配准方法有灰度信息配准方法[4]、特征配准方法[5]和变换域配准方法[6]。Kasar T等[7]使用欧氏距离调节最近邻(NN)与次近邻(SCN)距离的比值阈值，从而减少误匹配，但也容易失去一些正确的匹配点，不能真正提高匹配率。邹北骥[8]、H. Nicolas等[9]提出基于特征点的中值滤波算法，但该算法不能彻底排除匹配特征点的误差，而且耗时。Fang Xianyong等[10]提出RANSAC的初始迭代特征点对用中值滤波来检测，但误匹配对没有得到排除，算法效率没有得到明显提高。

就当前图像拼接算法存在复杂性和RANSAC算法迭代次数多的问题，文中提出了一种新的图像拼接算法。采用改进SIFT进行特征提取，降低了算法的复杂度。改进后的RANSAC算法，提高了算法的效率和配准稳定性。图像融合选择加权平均融合方法，实现图像的无缝拼接。

1 SIFT特征提取

1.1 SIFT算法

2004年David G.Lowe提出一种基于尺度空间的、对图像缩放旋转以及仿射变换仍保持不变的图形局部特征算子—SIFT[11]。详细步骤如下：

(1)构建高斯差分尺度空间。

D(x,y,σ)=(G(x,y,kσ)-G(x,y,σ))*I(x,y)=L(x,y,kσ)-L(x,y,σ)

(1)

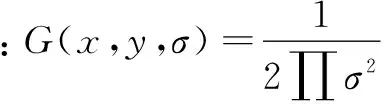
(2)高斯差分空间中寻找极值点，即特征点。

在整合三维二次函数后，精确定位极值点的位置和尺度，消除了对比度低和不稳定边响应点的点。边缘响应点通过式(2)去除。

(2)

式中，r为控制特征值大小的参数。

(3)为关键点分配方向。

为了让特征点具有局部旋转不变性，使用关键点邻域梯度像素的分布特性为每一个关键点分配方向参数，梯度的模和方向见式(3)和式(4)。

m(x,y)=

(3)

(4)

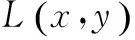
(4)形成特征点描述符。

最初把坐标轴旋转成关键点的主方向来保证旋转不变性，然后把以关键点为中心取的窗口平均分为16个小块，在每一个小块的8个方向梯度直方图上绘制每一个梯度方向的累加值，构成一个种子点，则每一个种子点含有8个方向的信息向量。描述了16个种子点，这是由128维矢量描述的特征点。

1.2 改进的SIFT特征点描述符

在步骤(3)中，特征点被分配一个主方向，并实现由局部区域特征点的抗旋转能力。考虑到圆具有良好的旋转不变性，兰视爽等[12]利用圆形区域周围的特征点构造SIFT特征描述子，当图像发生旋转时，子环中的像素位置发生了变化，其余的特征保持不变。

首先，计算圆环内每一个像素的梯度值和方向，统计出8个方向的梯度累加值。其次，对梯度累加值从大到小排序，确保旋转后排序值不变。最后，对这一向量进行归一化处理。

改进后的SIFT描述符自身具备旋转不变性，不需要通过旋转坐标轴来保证特征描述符的旋转不变性。同时，改进后的筛选描述符被减小到64个维度，从而大大提高了工作效率，降低了匹配特征点的复杂性。

2 特征点匹配与筛选

图像SIFT特征点提取后，从待匹配图像中选择正确特征点。林陆君等[13]采用优先k-d树从基准图像中查寻与该点欧氏距离最近的前两个特征点，获得距离最近的与次近的比值，若比值小于给定的阈值，则认为距离最近的点为匹配点。欧氏距离公式为：

(5)

其中，m=(m1,m2,…,mp)和n=(n1,n2,…,np)分别是两张图的特征向量。

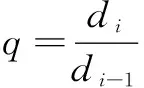
2.1 传统的RANSAC算法

为了增强算法的鲁棒性，周建平等[14]采用传统的RANSAC算法排除误匹配。步骤如下：

(1)按照置信概率P和数据错误率ω，以及所需的最小量的数据m来计算模型参数，由式(6)计算需要选择的抽样数量M：

(6)

(2)随机选择原始数据样本，估计每个样本的样本数量为模型参数所需的最小数据，并计算样本的相应模型参数。

(3)使用所有的原始数据来测试模型的参数，得到每个模型参数的正确数目；重复(2)、(3)步，直到完成M组抽样的处理。

(4)找出最优模型参数所对应的所有inliers，并用这些数据计算最终的模型参数。

2.2 改进的RANSAC算法

当匹配点中存在较多误匹配时，RANSAC的随机采样次数就会增多，造成运行缓慢，求出的变换矩阵精度不高，要对其进行改进。剔除原理如下：若(Pi，Qi)和(Pj，Qj)是一对正确匹配点，那么Pi和Pj的距离d(Pi,Pj)与Qi和Qj的距离d(Qi,Qj)是相似的。所以，利用Pi与第一幅图中所有感兴趣点Pj的关系和Qi与第二幅图中所有感兴趣点Qj的相似性来评价两点的对应关系，提出如下评价函数：

(7)

改进后RANSAC算法步骤如下：

(1)计算ω(i)的所有值；

(2)求出全部ω(i)的均值ω；

(3)判断ω(i)，如果ω(i)>0.8ω,Pi和Qi是正确匹配点，则保留，否则删除；

(4)将筛选出来的正确特征点作为RANSAC算法的初始迭代特征点对，求出精确的单应性矩阵H。

3 图像融合

图像配准好后，如果只是一个简单的叠加，会使图像模糊而且有明显的缝合线，造成不好的拼接。文中选用加权平滑法。

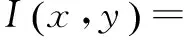
(8)

d1和d2的计算如下：设当前像素的横坐标为xi，重叠区域左右边界的横坐标分别为xl和xr，那么

4 实验结果及分析

实验所用的平台为VS2010和OpenCV，图像大小为340×280。选用4种典型的测试图进行测试，如图1所示。

特别说明的是：4组图像中左图为参考图像，右图为待拼图像。

首先，采用SIFT算法分别对图1中的4组图进行特征提取，确定图2(a)中SIFT特征点个数分别为1 376和1 071，图2(b)中的特征点个数分别为350和246，图2(c)中特征点个数分别为839和698，以及图2(d)的特征点个数分别为773和607。图中标注的箭头表示特征点的梯度信息，其中箭头方向表示特征点的梯度方向，而箭头长度表示特征点的梯度幅值大小。

然后，通过k-d树算法分别计算图2特征点，得到粗匹配点对并标注在测试图中：566对(图3(a))、121对(图3(b))、101对(图3(c))和230对(图3(d))。

图1 未提取特征点的测试图

图2 SIFT特征梯度描述

图3 特征粗匹配点对(1)

最后，通过RANSAC算法消除图3中存在的误匹配点对并计算出图像间的透视变换矩阵H，将待拼接图像变换到参考图像坐标系后进行渐进渐出图像融合，得到最后的拼接效果图。

由于在DOG空间中寻找极值点需要在三维平面中进行搜索并且搜索的层数较多造成图3中检测的特征点较大，搜索时间长。同样，图3中显示特征点粗匹配数目较大，然而计算透射变换矩阵H仅需要4对特征点对，这导致RANSAC算法剔除误匹配点的计算量增大，从而消耗内存，计算时间较长。

采用文中提出的改进的SIFT和RANSAC算法，对图像进行特征点提取，并通过设定阈值T的大小来限制图像特征点的个数。经过粗匹配后，粗匹配点对分别降为：199对(图4(a))、15对(图4(b))、18对(图4(c))和18对(图4(d))。

图4 特征粗匹配点对(2)

采用RANSAC算法来消除误匹配点对并用透视变换公式分别计算出图3中待拼接图像的坐标变换矩阵H中的参数：

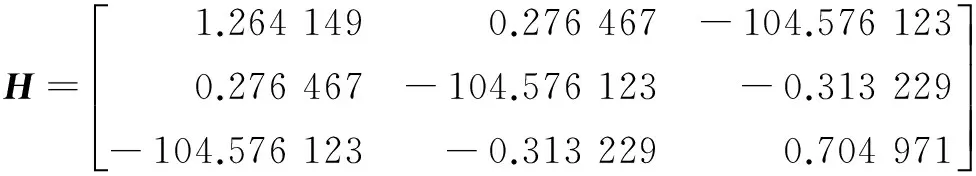
矩阵H的参数确定后，即分别得到了待拼接图像的透射变换图，将得到的透视图与图1中的参考图像分别进行渐进渐出融合，得到图5所示的最终融合图像。

图5 融合图

表1为选用同一组测试图所得的特征点个数、匹配点数及拼接所消耗时间。

由表可分析得出,采用所提方法的粗匹配对数、一致集的匹配对数、匹配精度和拼接耗时都有了明显的改善。

表1 SIFT算法与改进SIFT算法对图像的实验结果

5 结束语

文中提出了一种改进SIFT和RANSAC的图像拼接算法，提高了配准速率，相对于SIFT算法的图像拼接有明显的提高。由于初始配准中存在错误匹配点，采用RANSAC算法剔除误匹配点来获得准确的区域匹配，和坐标变换矩阵的特征点计算是正确的。这样，既满足了单应性矩阵的估算精度，又具备一定的拼接效果和鲁棒性。

[1] 张 琳,褚龙现.基于全局拼接的航拍图像拼接算法研究[J].计算机仿真,2012,29(4):282-285.

[2] 万 雪,张祖勋,柯 涛.一种利用零交叉点理论的改进SIFT特征提取算法[J].武汉大学学报:信息科学版,2013,38(3):270-273.

[3] 雒伟群,高 屹.基于改进RANSAC算法的图像拼接方法[J].科技创新与应用,2015,26(5):21-22.

[4] 廖 飞,叶玮琼,王鹏程,等.基于SIFT特征匹配的图像拼接算法[J].湖南工业大学学报,2014,28(1):71-75.

[5] 焦丽龙,韩 燮,李定主.改进的基于特征点匹配的图像拼接融合算法[J].计算机工程与设计,2014,35(3):918-922.

[6] 黄大坤,陆冬良,严志明,等.多图无缝拼接的配准算法[J].微型电脑应用,2014,30(2):62-65.

[7]KasarT,RamakrishnaaAG.Block-basedfeaturedetectionandmatchingformosaicingofcamera-captureddocumentimages[C]//ProcofIEEEregion10conference.Taipei:IEEE,2007:1-4.

[8] 邹北骥,阮 鹏,向 遥，等.一种精确匹配的全景图自动拼接算法[J].计算机工程与科学,2010,32(8):60-63.

[9]NicolasH.Newmethodsfordynamicmosaicking[J].IEEETransactionsonImageProcessing,2001,10(8):1239-1251.

[10]FangXianyong,ZhangMingmin,PanZhigeng,etal.Anewmethodofmanifoldmosaicforlargedisplacementimages[J].JournalofComputerScienceandTechnology,2006,21(2):218-223.

[11] 周 颖.基于SIFT算法的图像特征匹配[J].现代计算机,2015(5):63-68.

[12] 兰世爽,孙劲光.基于改进SIFT的抗几何攻击的数字水印[J].计算机工程与应用,2011,49(7):200-203.

[13] 林陆君,孙玲玲,李训根,等.一种改进的基于模板匹配的显微细胞图像拼接算法[J].计算机应用与软件,2010,27(1):108-110.

[14] 周建平,杨金坤,郑 宇.基于改进SIFT特征匹配的视频拼接—在倒车系统中的应用[J].企业技术开发,2011,30(22):70-71.

Research on Panorama Image Mosaic Algorithm Based on Improved SIFT and RANSAC

MA Qiang,XIANG Zhao-bao,HUANG Liang-xue,WANG Bo-hua

(Key Laboratory of Industrial Internet of Things & Network Control of MOE, Chongqing University of Posts and Telecommunications,Chongqing 400065,China)

In order to solve the problems of the complexity for the image mosaic algorithm and the large number of iteration for RANSAC,a panorama image mosaic algorithm is proposed in this paper.By feature points extraction,the image registration and weighted average fusion method,image stitching is conducted.The improved algorithm is used to extract the feature points,reducing the complexity of algorithm.In addition,the improved RANSAC algorithm can be used to reduce the number of iterations.Experimental results show that the improved method has lower computing load and increases the speed,besides,splicing efficiency has been significantly improved.

image mosaic;SIFT;RANSAC;image fusion

2015-09-14

2015-12-22

时间：2016-03-22

国家自然科学基金资助项目(60975008)；重庆市教委科学技术研究项目(KJ130529)

马 强(1990-)，男，硕士，研究方向为图像处理；项昭保，教授，研究方向为天然化合物的分离纯化、结构鉴定和结构修饰。

http://www.cnki.net/kcms/detail/61.1450.TP.20160322.1522.104.html

TP301.6

A

1673-629X(2016)04-0061-05

10.3969/j.issn.1673-629X.2016.04.013