基于欧氏比的快速分形编码算法

张爱华，何雨虹，张 璟

(南京邮电大学 理学院，江苏 南京 210046)

基于欧氏比的快速分形编码算法

张爱华，何雨虹，张 璟

(南京邮电大学 理学院，江苏 南京 210046)

分形编解码的时间过长，主要是因为编码过程中的搜索码本块的最佳匹配块占据了大量时间。如果能用某种方式，尽量缩短搜索码本块最佳匹配块的时间，那么分形编解码的时间就能大大缩短。文中提出了一种基于欧氏比的分形编码算法并给出了可行性分析。该算法将全局搜索最佳匹配块的算法转变为相对意义下的邻域搜索最佳匹配块的算法，即只搜索与R块的欧氏比相差较近的码本块，从而大大减少了搜索最佳匹配块所占用的时间,进而缩短了分形编解码的时间。用MATLAB对文中算法进行代码仿真，仿真效果用主观上观察图像的清晰度、图像编解码前后的信噪比和编解码的时间来评价。实验结果表明：该算法在尽量保证图像质量的前提下，使得分形编解码的时间大大缩短。

分形；分形图像编码；矢量叉乘向量；欧氏比

0 引 言

随着科学技术的发展，图像压缩引起了人们广泛的兴趣。同时，“分形”概念为复杂的自然景物的描述提供了一种有力的数学工具，之后，分形几何理论被应用在图像编码[1]，进而产生了比较新颖的图像编码方法—分形图像编码算法[2-4]。而分形图像编码的高压缩比、多分辨率以及较好的重构图像质量等特点，使得它的编码算法研究十分活跃。目前，分形图像编码研究还不是很成熟[5-6]，很多问题有待进一步探索。而这些研究的目的主要是为了改善以下几个方面：压缩比、编解码速度、重构图像质量。而固有的编码耗时限制了分形编码的发展。

近年来，许多专家和学者在分形图像编解码时间和重构图像质量等方面做了大量的研究[7-11]，也获得了一些成果，但是在保证一定图像质量的前提下缩短编解码时间仍然是研究的一个重要问题。而分形图像的编码中，从海量码本中搜索每个R块的最佳匹配码块占去了分形图像编码的大部分时间。目前在匹配方面，主要分为对图像子块进行分类和建立子块特征，前者将全局搜索转化为类内搜索来缩短编解码时间，后者是在子块特征的基础上将全局搜索转化为局部搜索来缩短编解码时间。而这种将全局搜索转化为局部搜索(类内搜索)其实有时并不能准确地、全面地反映子块与父块间的适配程度，但是文中算法研究发现，在一定的误差范围内，局部搜索是可以代替全局搜索的。如果能按照这种方式将不太可能匹配的R块排除，那么编码时间将会大大减小。这是大多数快速分形图像编码算法的基本思想。

基于这种想法，文中定义了图像子块的一种新特征—欧氏比，将“MSE意义上的最佳匹配”转化到“图像欧氏比特征空间的领域搜索”，大大减少搜索空间，加快编码速度[12-13]。此外，分析并给出了该特征与匹配误差之间的关系，基于这一关系提出了一种快速分形图像编码算法。

1 基本分形方法简介

1.1 图像分割

假定待编码图像F是N×N灰度图像，像素灰度值按照8比特量化(即把灰度值分为256级)。在应用中，N一般为2的方幂，例如256，512等。采用固定方块分割的方法，把图像I分割成一系列大小固定的B×B像素子块Ri(它们互不重叠且能够覆盖整幅图像)，也就是说：

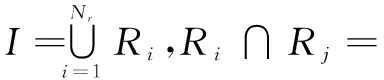
在分形编码中，这种子块称为Range块(以下简称R块)，应用中尺寸一般为4×4，8×8，16×16等，文中取R块为8×8。在由R块组成的子块中，通常按行序逐块编码，即把R块排列成：

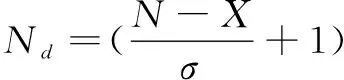
1.2 码本构成

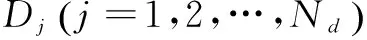
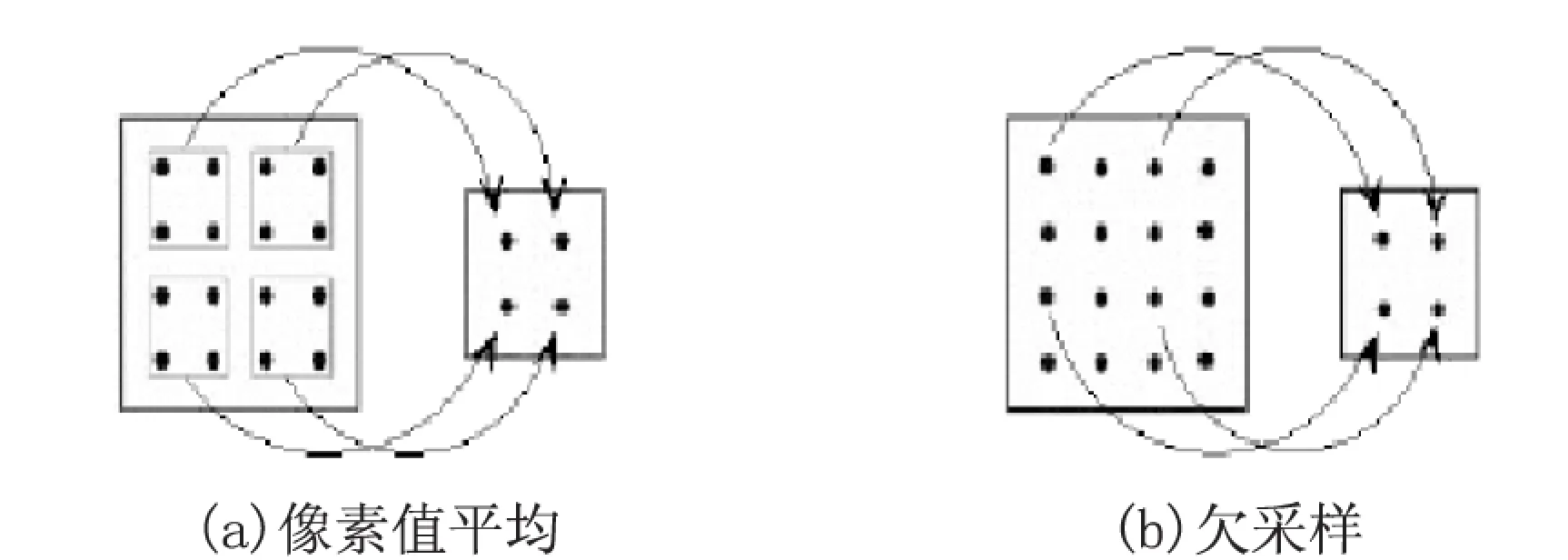
图1 收缩D块的构造

这种收缩子块的全体就构成“虚拟码本”，记这个码本为Ω，即

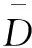
(1)恒等变换：(t0D)i,j=Di,j;

(2)关于铅垂中轴(j=B-1/2)对称的反射：(t1D)i,j=Di,B-1-j;

(3)关于水平中轴(i=B-1/2)对称的反射：(t1D)i,j=DB-1-i,j;

(4)关于主对角线(i=j)对称的反射：(t3D)i,j=Dj,i;

(5)关于次主对角线(i+j=B-1)对称的反射：(t4D)i,j=DB-1-j,B-1-i;

(6)关于D块的中心逆时针旋转90°：(t5D)i,j=Dj,B-1-i;

(7)关于D块的中心逆时针旋转180°：(t6D)i,j=DB-1-i,B-1-j;

(8)关于D块的中心逆时针旋转270°：(t7D)i,j=DB-1-i,j。

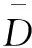
1.3 编码匹配阶段

E(R,D)=

然后记下D块位置，变换的类型以及s和o的值。

1.4 解码阶段

分形解码较为简单，重构的图像是分形码描述的压缩变换T的近似的不动点图像，可以按照分形码提供的分割信息对任何初始图像进行迭代来生成。不动点定理可保证迭代的收敛性，而拼贴定理则可保证压缩变换T的不动点就是原图像的近似[15-16]。

2 算法理论依据

首先给出一个比较简单的结果：给定R,D∈Rn×n，以及最小值的问题：

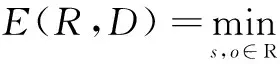
显然,‖R-sD-oI‖2是关于s和o的二次多项式，分别对s和o求偏导，并令导数值为零，解关于s和o的一个线性方程组，解其得：

在分形编码中，每个R块是由它的最佳匹配块D∈Ω的灰度变换来近似得到的，即

R≈s·D+o·I

下面定义了图像子块的一种新的特征，给出该特征与匹配误差之间的关系。然后，基于这种关系提出一种快速分形图像编码算法[17-19]。

将每一图像子块R与D均分为四个部分(见图2)，求出各部分的灰度均值，根据它们的空间位置，令其对角线两元素之差组成矢量叉乘向量：

由上述方法分别求得子块R与父块D的子块矢量叉乘向量r,d。

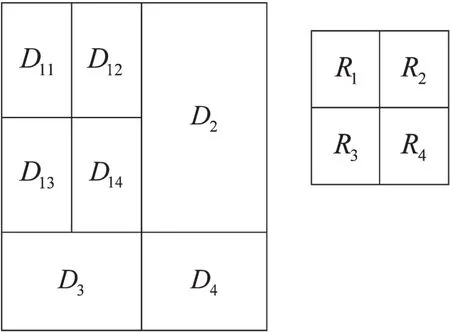
图2 D块(左)和 R块(右)

定义：设子块R=(r)，记

特征C(R)是通过子块叉乘向量的欧氏距离定义的，故把它称为欧氏距离比率特征，简称为欧氏比。

下面给出特征C(R)的可行性分析。

R≈s·D+o·I

Rin=s·Djn+o·I(n=1,2,3,4)

r=s·d

ri=s·di

显然有

因此得

C(R)≈C(D)

3 算法分析与实现

3.1 算法分析

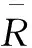
显然，这种做法不仅提高了重构图像质量，还能通过减少码块的数目来加快编码的速度。

为了降低邻域搜索较小时，局部的搜索匹配子块代替全局的匹配块而引起图像质量下降这一缺点，应注意以下几点[20]：

(1)设定阈值t，这一点可以保证在与R块欧氏比相差最小的Dm块的t邻域内寻找最佳匹配的码块D。

(2)设定一个误差阈值H，来保证这种误差不至太大，从而使得解码图像质量得以保证。

3.2 算法的实现

基于3.1的分析，算法的具体步骤如下：

Step1：图像的分割与码本的构成。把图像分割成不重叠的B×B块(R块，记为R),同时，以纵横方向步长均为x像素生成尺寸为2B×2B的D块池。对于每个D块，采用4-邻域像素值平均得到B×B块，这样的子块集合构成码本Ω。

Step2：参数的初始化。设定R子块的标准差阈值为y1，码块标准差阈值为η，误差阈值为H,初始邻域半径为t，扩域步长为L。

Step4：对于子块R：

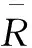
(2)若σR≥y1，对于每个R子块，计算出C(R),并用二分法在上述排好序的容许码本中搜索与C(R)相差的最小的D块，并记为Dm。

Step5：搜索最佳的匹配块。

(1)设定误差阈值为H。

(2)设置临时变量为t，并初始化t=k。

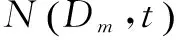
(4)否则，令t=t+L，转步骤(3)。

Step6:记录R的最佳匹配块D的位置，s和o的值以及变换类型。

Step7：对于其余子块R，重复步骤4～6。

4 实验仿真结果

在实验中[22]，用MATLAB7.0作为实验平台，选用512*512大小的Lena图像进行实验，实验结果用峰值信噪比(PSNR)和编码的时间来表示。t为搜索邻域半径，并取D块标准差阈值η为1 225，R块标准差阈值y1为1，实验结果见图3～5(图中t=3)。

分形图像压缩改进主要集中在缩短编解码时间、提高解码图像质量这两个方面。而文中算法自定义一种子块匹配特征，旨在保证一定解码图像质量的前提下尽量缩短编解码时间。下面，以相对梯度特征来作为最新颖的特征匹配算法的一个代表，将文中算法的欧氏比C(R)换成相对梯度特征,其他量基本不变来进行代码仿真，并输出其编解码的时间以及信噪比。

图3 原图

图4 实验结果图

图5 相对梯度特征算法实验结果图

表1给出了文中算法与基本分形算法以及相对梯度算法效果的比较。其中，以t表示编解码的时间，以信噪比表示重构图像质量。

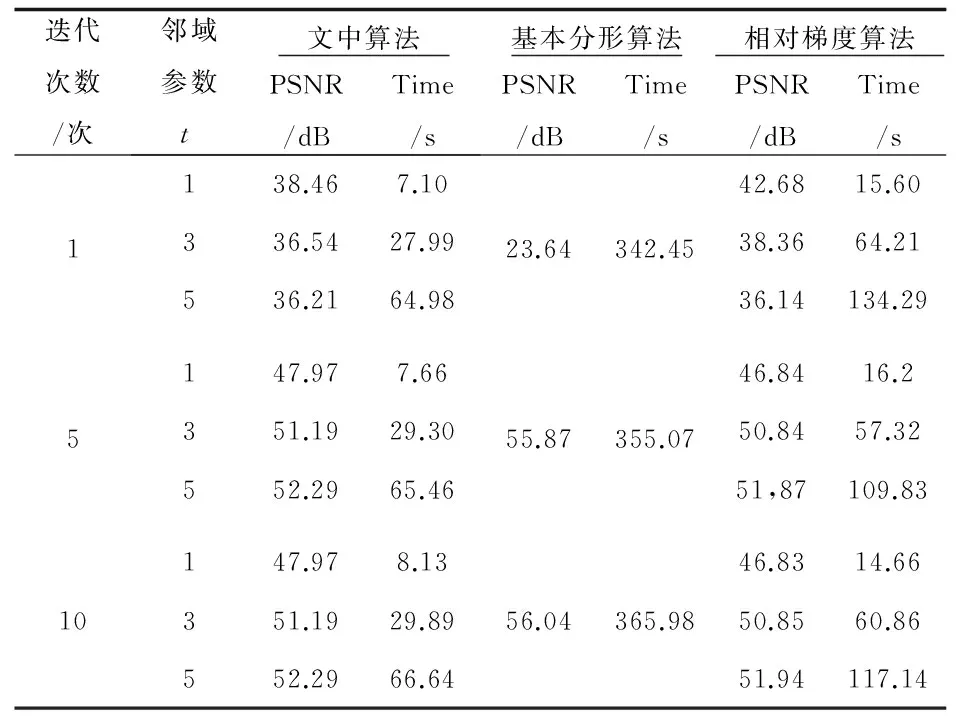
表1 文中算法与基本分形算法对比结果 (测试图像：Lena)

分析实验结果可得，主观上，基于欧氏比的快速分形编码算法的重构图像质量基本不变;客观上，主要从两个角度来看：其一，编解码时间。以此来衡量基于欧氏比特征的分形编解码的速度，而文中算法的编解码时间和基本分形编码以及子块特征编码中比较新颖的相对梯度算法比较，结果显示，编解码时间缩短的更加明显；其二，重构图像的信噪比。以此来衡量重构图像的质量，通过对比，文中算法的信噪比基本没变，从而在尽量保证一定信噪比的前提下，编解码时间可以大大减少。

5 结束语

由于基本分形编码时间过长，文中提出了一个基于欧氏比的改进方法来寻找最佳匹配块，以缩小码本块搜索的范围，提高编解码的速度。引进了参数t，η和y1，在尽量保证图像质量不变的条件下，缩短编解码的时间。实验结果表明，文中算法相对基本分形的算法应用前景更加广阔。

此外，文中算法还存在许多不足之处，比如信噪比基本没有改善等，这些问题都是今后需继续研究改善的，也是今后研究的重点。而为了在缩短编解码时间时，尽量改善图形质量，笔者将尝试将文中的子块特征与其他能够较好描述图像纹理细节及其他一些特征的量(如：分形维数、小波、DCT变换等)相结合来编写分形算法，以此来改善重构图像的质量。而目前也有大量专家在这种混合编码方向进行了研究，同时也取得了不少成果。从这些成果来看，一些混合编码对分形图像编码的编解码时间和重构图像的质量上都有所改善,故预计将文中算法与其他子块特征结合进行混合编码能够取得预期的效果，这也是之后研究与探索的重点。

[1]WohlbergB,deJagerG.Areviewofthefractalimagecodingliterature[J].IEEETransactionsonImageProcessing,1999,8(12):1716-1729.

[2]FisherY.Fractalimagecompress:theoryandapplication[M].NewYork:Spring-Verlag,1995.

[3]ShiYipen,GuWei,ZhangLiming.Somenewmethodstofractalimagecompression[J].CommunicationinNonlinerScience&NumericalSimulation,1997,13(2):80-85.

[4]ZhaoYao,YuanBaozong.Imagecompressionusingfractalsanddiscretecosinetransform[J].ElectronicsLetters,1994,30(6):474-475.

[5] 田 岩，彭复员.数字图像处理与分析[M].武汉:华中科技大学出版社,2009.

[6] 刘忠艳,周 波,车向前.一种高效的图像匹配算法[J].计算机技术与发展,2009,19(4):45-47.

[7]YamaguchiH.EfficientencodingofcoloredpicturesinR.G.Bcomponents[J].IEEETransactionsonCommunications,1984,32(11):1201-1209.

[8]LaiCM,LamKM,SiuWC.Afastfractalimagecodingbasedonkick-outandzerocontrastconditions[J].IEEETransactionsonImageProcessing,2003,12(11):1398-1403.

[9]PopescuDC,DimcaA,YanH.Anonlinearmodelforfractalimagecoding[J].IEEETransonImageProcessing,1997,6(3):372-382.

[10]HeC,YangSX,HuangX.Variance-basedacceleratingschemeforfractalimageencoding[J].IEEEElectronicsLetters,2004,40(2):115-116.

[11]JacquinAE.Anovelfractalblock-codingtechniquefordigitalimage[C]//ProceedingsofIEEEinternationalconferenceonASSP.[s.l.]:IEEE,1990.

[12] 陈衍仪.图像压缩的分形理论和方法[M].北京:国防工业出版社，1997.

[13] 陈守吉，张立明.分形与图像压缩[M].上海:上海科技教育出版社，1998.

[14] 李高平.分形图像压缩编码[M].成都:西南交通大学出版社，2010.

[15]BeaumontJM.Imagedatacompressionusingfractaltechniques[J].BritishTelecomTechJournal,1991,9(4):93-109.

[16]BarnsleyMF,HurdLP.Fractalimagecompression[M].Wellesley:AKPeters,1992.

[17]PolvereM,NappiM.Speedupinfractalimagecoding:comparisonofmethods[J].IEEETransactionsonImageProcessing,2000,9(6):1002-1009.

[18]MelnikovG,KatsaggelosAK.Anonuniformsegmentationoptimalhybridfractal/DCTimagecompressionalgorithm[C]//ProcofIEEEinternationalconferenceonacoustics,speech&signalprocessing.[s.l.]:IEEE,1998:2573-2576.

[19]TruongTrieu-Kien,JengJyh-Horng,ReedIS.AfastencodingalgorithmforfractalimagecompressionusingtheDCTinnerproduct[J].IEEETransactionsonImageProcessing,2000,9(4):529-534.

[20] 庄振静.分形图像压缩的两个快速编码算法[D].重庆:重庆大学,2009.

[21]JacobsEW,FisherY,BossRD.Imagecompression:astudyoftheiteratedtransformmethod[J].SignalProcessing,1992,29(3):251-263.

[22] 杨 帆，王志陶，张 华.精通图像处理经典算法[M].MATLAB版.北京:北京航空航天大学出版社，2014.

A Fast Fractal Image Coding Algorithm Based on Euclidean Ratio

ZHANG Ai-hua,HE Yu-hong,ZHANG Jing

(College of Science,Nanjing University of Posts and Telecommunications,Nanjing 210046,China)

Searching for the best matching block in coding processing occupies a lot of time,which is the main reason for the time of fractal encoding and decoding being too long.If one way is applied to shorten the time of searching the best matching block,the time of fractal encoding and decoding could be sharply decreased.A fractal image coding algorithm based on Euclidean ratio was proposed and the feasibility analysis was given.The algorithm transforms the global searching to the neighborhood searching,which means that only need to search the code block whose Euclidean ratio closes to R block’,the time of searching for the best matching block could be greatly reduced,thus shortening the time of fractal encoding and decoding.Code simulation was conducted for this algorithm by MATLAB.The indicators include image clarity,PSNR before and after encoding and decoding,and the time for encoding and decoding.The experimental results show the algorithm have been improved in terms of encoding time on the premise of guaranteeing the image quality.

fractal;fractal image coding;vector cross product of vectors;Euclidean ratio

2015-03-30

2015-09-04

时间：2016-01-26

国家自然科学基金面上项目(11471114,61372125);南京邮电大学攀登计划一项(NY210018)作者简介：张爱华(1969-)，女，教授，博士，研究方向为非线性分析及其应用。

http://www.cnki.net/kcms/detail/61.1450.TP.20160126.1521.072.html

TN919.81

A

1673-629X(2016)02-0061-05

10.3969/j.issn.1673-629X.2016.02.014