多端直流的交直流配电网潮流计算

刘耀华，裴玮，杨艳红，赵振兴，邓卫，于汀，黄仁乐

(1.中国科学院电工研究所，北京市 100190；2.中国科学院大学电子电气与通信工程学院，北京市 100190; 3.中国电力科学研究院，北京市 100192；4.国网北京市电力公司，北京市 100031)

多端直流的交直流配电网潮流计算

刘耀华1，2，裴玮1，杨艳红1，赵振兴1，邓卫1，于汀3，黄仁乐4

(1.中国科学院电工研究所，北京市 100190；2.中国科学院大学电子电气与通信工程学院，北京市 100190; 3.中国电力科学研究院，北京市 100192；4.国网北京市电力公司，北京市 100031)

传统的交直流潮流计算方法主要用于输电网计算，而交直流配电网需要考虑交流网侧三相不平衡和直流网侧分布式电源低压多端直流接入等问题。针对这一问题，提出了一种考虑三相不平衡的含多端直流的交直流配电网交替求解算法。(1)对交流系统和换流站三相不平衡建模；(2)计及换流站不同控制方式，推导了直流潮流方程，在其基础上，推导了含DC/DC变换器的直流潮流计算修正方程式，根据DC/DC变换器和换流站控制方式的不同，在交直流潮流计算中提出不同的等效处理方式；(3)通过改进的IEEE 34节点算例进行了仿真验证。仿真结果表明，在多端直流不同控制模式下，所述交直流配电网潮流计算方法处理三相不平衡、分布式电源直流接入等问题具有较好的收敛性能。

多端直流；配电网；补偿电流； DC/DC变换器；交替求解算法

0 引 言

随着新能源、新材料以及电力电子技术的快速发展与广泛应用，用户对供电质量、可靠性以及运行效率等要求日益提高，现有交流配电网正面临用电需求多样化、分布式发电规模化接入、潮流协调控制复杂化等多方面的巨大挑战。一方面，光伏、燃料电池等分布式发电大规模接入配电网；另一方面，配电网中用电设备的形态和数量发生了一定变化，大量电动汽车、储能设备、LED照明等直流设备广泛使用。为此必须采用新技术、新设备、新拓扑来满足未来供电局面的变换，而发展多端低压直流技术是解决这一问题的有效手段之一。如果采用直流接入方式，可以省去变换环节，提高整体的运行效率。由于交流设备仍是目前配电网中用电负载的主要形式，直流设备的接入会形成未来长时期交直流负载共存的局面。因此多端直流[1]的交直流配电网潮流计算研究具有重要意义。

单纯的交流配电网潮流计算已较为成熟，而用于电压多端交直流配电网潮流计算，依然是一个研究热点。交直流潮流计算主要分为统一迭代法和交替迭代法，统一迭代法利用交流节点电压的幅值和相角与直流系统的电压、电流以及换流站变比、功率因素、换流站控制角统一进行迭代求解[2-5]。交替迭代法将直流潮流与交流潮流方程分开迭代求解，交替迭代，直到收敛为止[6-7]。交替迭代法由于其灵活性和良好继承性，获得了较多的重视。许多国内外学者对含电压源型高压直流(voltage sourced converter-high voltage direct current，VSC-HVDC)系统交直流潮流计算有过大量的研究，已经取得了比较丰富的成果，文献[8]根据换流站不同运行控制方式，列出了交直流交替求解的接口方程，实现了基于等值功率注入的VSC-HVDC潮流计算算法。文献[9-10]主要针对两端VSC-HVDC系统的交直流潮流计算。文献[11]对多端VSC-HVDC系统模型的建立，允许有多个AC和DC网络，计及了换流站损耗，以及各种控制方式，形成了交替迭代算法，最后基于文献中提到的算法，开发了开源软件MATPOWER。文献[12]提出了一种基于双向迭代的混合潮流计算方法，该方法能够保留统一迭代法的收敛性，同时又可继承交替迭代法控制方式切换简易的特点。上述交直流潮流算法有一个共同点，研究主要集中在高压交直流输电网络。

本文主要研究交直流配电网，配电网与输电网有较大差异，如：配电网需要考虑三相不平衡，配电网中直接接入一些直流负荷，以及将风电、光伏、燃料电池直接接入直流母线，因此原有的输电网交直流潮流模型无法直接应用于配电网交直流潮流计算。本文从交流、电压源型换流站(voltage sourced converter,VSC)三相不平衡潮流模型出发，推导交直流潮流模型，在其基础上建立DC/DC变换器模型，推导含DC/DC变换器的直流潮流计算修正方程式，根据变换器和换流站控制方式的不同，提出不同的处理方法，充分考虑配电网的不对称性，发展配电网交直流混合潮流计算方法。最后通过改进的算例对模型和算法的有效性进行验证，采用交替迭代的交直流潮流程序具有结构清晰、编程简单，程序通用性好的优点。

1 交流不平衡模型

交流电力网络建模分2类元件，一类为功率转换元件(power conversion ，PC)，另一类为功率传输元件(power delivery，PD)，通常PC元件是非线性元件，PD元件是线性元件。交流网络中的线路、变压器、电容器等可以归结为PD元件，负荷、发电机、电流源、电压源等可以归为PC元件，负荷元件进行诺顿等效为元件的导纳Yprim与补偿电流I的并联，补偿电流用来补偿非线性部分，如图1所示。

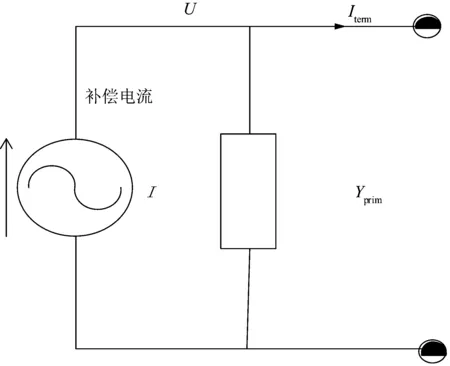
图1 PC元件等效模型Fig.1 Equivalent model of PC element

文献[13]给出了三相配电线路的各种元件Yprim的推导过程，不同类型负荷、发电机等PC元件都可以用文献类似的方法推出各个元件的Yprim。不失一般性，假设一个交流系统有n个节点，其中m个节点处有PC元件，n-m节点处有PD元件，含PD元件的节点处其补偿电流为0，则有

(1)

式中：上标t∈{a,b,c}三相；k表示交流潮流第k次迭代；系统导纳矩阵Ysys，包含负荷元件和发电机元件的Yprim，而通常传统潮流计算方法系统的导纳Ysys不含负荷元件和发电机形成的Yprim。PC元件中的负荷元件，由图1可知，负荷的补偿电流与节点电压存在如下关系

(2)

式中：Pspec，Qspec表示给定的有功和无功功率；Ut表示节点处的电压。

其他PC元件的补偿电流It,k+1也可以通过类似原理推导出，从式(2)可以看出补偿电流与节点电压存在非线性关系，需要求解非线性方程，通常有迭代法、对分法以及牛顿法，本文运用固定迭代法。利用式(1)，式(2)反复迭代计算，直到电压收敛为止，由于整个计算过程中无需形成雅克比矩阵，计算过程中，系统的导纳矩阵Ysys保持恒定不变，能够加快交直流潮流计算速度。交流计算流程可以参考文献[13]。

2 VSC的换流站不平衡模型

2.1 换流站模型

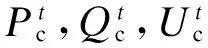
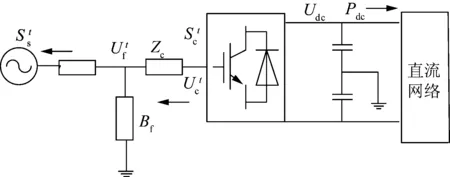
图2 VSC-HVDC交直流输电模型图Fig.2 Equivalent AC/DC transmission model of VSC-HVDC

(3)

(4)

2.2 控制方式

由于换流站的电流解耦控制，有功功率和无功功率能够独立控制，无功功率控制方式[11]有：(1)恒无功功率控制，注入交流系统的无功功率Qs是恒量；(2)恒电压控制，通过调整换流站无功功率，使得交流节点的电压Us保持不变。换流站有功功率有3种控制方式：(1)恒有功功率，如图3(a)所示，换流站注入交流系统的有功功率Ps保持恒定不变；(2)恒电压控制方式，如图3(b)所示，换流站直流侧的电压Udc保持恒定不变；(3)下垂控制方式，如图3(c)、3(d)所示，分别为电压对功率下垂和电流对电压下垂，下垂控制主要是指各个换流站会按照直流功率-电压斜线和直流电压-电流斜线实现功率分担，保证直流电压稳定。下垂系数kdc决定了换流站中不平衡的有功功率分配的多少，较大的kdc意味着换流站将分担较小的不平衡功率，较小的kdc意味着换流站分担较多的不平衡功率。

图3 换流站有功功率稳态控制方式Fig.3 Steady-state active power control mode forconverter station

2.3 换流站不平衡补偿

(5)

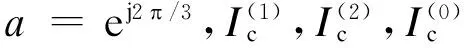
3 直流侧模型

3.1 直流网络方程

DC网络中不同节点的功率取决于不同节点的电压，假设DC网络有n个节点，第i个DC节点的注入电流，等于其余n-1个节点流入这个节点的电流之和，则有

(6)

式中：Udci、Udcj分别表示节点i、j处的电压；Ydcij表示节点i、j之间的导纳。

对称接地单极型直流电网，注入节点i的有功功率可以表示为

(7)

联立式(6)、(7)，得到直流潮流计算方程

(8)

对于下垂控制方式为电压对功率的换流站，其DC侧的有功功率与潮流计算的电压偏离参考电压的差值以及下垂系数有关，假设i表示第i个下垂控制的换流站，电压对功率下垂控制，则有

(9)

对于电压对电流下垂控制方式，则有

(10)

式中：Pdc,0、Udc,0i、Idc,0i分别表示下垂控制功率设定初始值，电压设定初始值，电流设定初始值。电压对功率下垂控制的下垂系数ki定义为ΔUdc/ΔPdc，电压对电流下垂控制的下垂系数ki定义为ΔUdc/ΔIdc。联立式(8)、(10)，则有

(11)

式(11)反映的是利用电压对电流下垂控制的功率与直流潮流计算的功率的差值，最终直流潮流收敛，其差值为0。

3.2DC/DC变换器模型

DC/DC变换器能够实现电压的变换，其两侧的功率、电压可以独立控制，变换器的损耗与电压、电流成非线性关系。变换器的损耗主要有开关损耗、变压器损耗、电容损耗、二极管损耗、输出滤波电感损耗等。在建立变换器模型之前，作出如下假设，在直流网络节点p，q处有DC变换器。变换器两端有以下几种控制方式：(1)U-I或者U-P下垂控制；(2)恒P控制；(3)恒U控制。变换器两端控制方式可以是这几种组合，DC/DC换流站模型如图4所示。

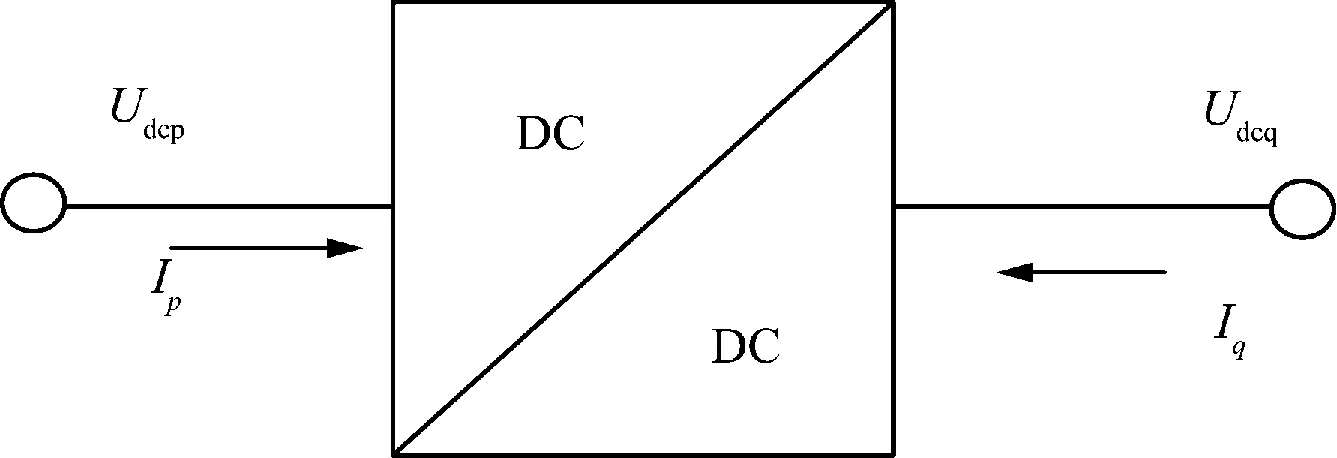
图4 DC/DC变换器模型Fig.4 DC/DC converter model

计及变换器损耗，则有：

(12)

(13)

E=UdcpIp+UdcqIq-Ploss

(14)

式中：Pp、Pq分别为节点p、q的功率；E为功率平衡方程；Ploss为DC/DC变换器的损耗；Ydcpj为节点p、j之间的导纳。损耗与电压、电流成非线性关系，DC/DC变换器的损耗的计算取决于变压器与电子器件材质、电路拓扑，不同电路拓扑损耗的计算公式不同，文献[14-18]对损耗的计算进行了详细的分析，下面给出Buck电路损耗的计算公式。

(15)

(16)

(17)

(18)

(19)

(20)

Ploss=PrDS+PRF+PVF+PrL+PrC

(21)

式中：rc为滤波电容等效电阻；fs为开关频率；L为电感值；rDS为MOSFET管等效电阻；R为负载电阻；UF为二极管等效平均电压；RF为二极管电阻；rL为电感电阻；PrC、PrDS、PRF、PUF、PrL分别为滤波电容、MOSFET管导通电阻、二极管、等效偏置电阻、电感的损耗；D是占空比。

3.3 含DC/DC变换器直流潮流雅克比矩阵

在计算直流潮流前，直流侧注入电流Idci是未知量，需求取换流站直流侧电压，对于DC平衡节点，其直流侧电压是给定的，注入功率是未知量，而其他控制方式的电压是未知量，注入功率是已知量，DC系统方程是非线性方程，用牛顿法[19]进行推导。计算交流潮流，可以得出换流站注入直流侧的功率，若直流母线接入含DC/DC变换器的负荷，这个节点的功率是给定的，其功率流向与换流站注入功率方向相反。不失一般性，假设第1个直流节点为平衡节点，2到m节点为P-U的下垂控制，功率设定为Pdc,0i，i表示第i个节点。m+1到k节点的功率设定为Pdc,i，节点k+1到n为U-I的下垂控制，电流设定Idc,0i，电压设定为Udc,0i，对于含DC/DC变换器的负荷都可归为功率设定为Pdc,i，则功率修正量有：

(22)

式中：上标k表示交直流迭代计算的主循环迭代次数；上标j表示DC潮流计算迭代次数。根据式(5)—式(8)、式(22)按泰勒级数展开，略去高次项后，可得牛顿法潮流方程

ΔP=JΔU

(23)

式中J为雅克比矩阵。节点2到k有如下偏导：

(24)

(25)

(26)

(27)

节点k到n，根据式(11)则有：

(28)

(29)

根据式(24)—式(29)可以写出雅可比矩阵J，不失一般性，假设在p、q节点处接入DC/DC变换器，变换器的p侧是恒功率控制，q侧是恒电压控制，由式(11)—式(13)，可以推出新的直流系统方程为

(30)

根据式(30)，新的雅克比矩阵J′需要增加2列，更新第q行q列的数据，另外需要增加2行节点p处功率和平衡方程与电压以及电流Iq和Ip之间的偏导关系，新的雅可比矩阵为

(31)

由式(14)有新的雅可比矩阵中平衡方程对电压Udcq、电流Iq和Ip之间的偏导关系为：

∂E/∂Udcq=Iq-∂Ploss/∂Udcq

(32)

∂E/∂Ip=Udcp-∂Ploss/∂Ip

(33)

∂E/∂Iq=Udcq-∂Ploss/∂Iq

(34)

对于DC网络有m个这样的DC/DC变换器，则雅可比矩阵可以类似推出，J′将是(n+2m)×(n+2m)矩阵。由式(15)—式(21)可以推出损耗对电流、电压的偏导数。

4 交直流潮流计算

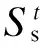
表1 节点等效处理
Table 1 Node equivalent processing

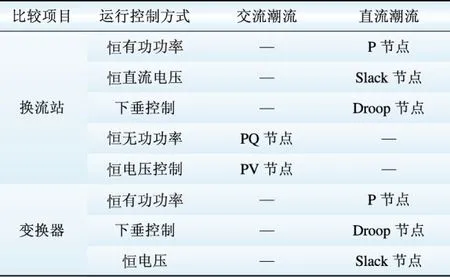
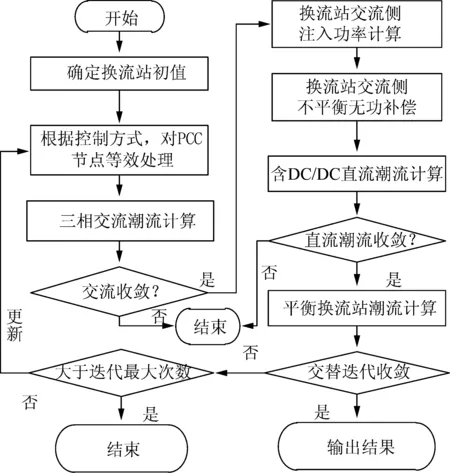
图5 交替迭代求解流程图Fig.5 Flow chart of AC/DC sequential iteration method

5 算例仿真

本文以图6所示的改进型IEEE 34节点的交直流混合系统为例，在IEEE 34算例的806，814，830节点处分别接入1，2，3换流站，换流站的直流侧互相连接，形成1个环网。换流站1，2，3的参数一致，换流变压器的阻抗，Ztf=0.015 pu+j0.112 pu，相电抗器的阻抗Zc=0.000 1 pu+j0.642 8 pu。换流站1的初始功率P1=60 kW,Q1=40 kvar;换流站2的初始功率P2=-30 kW，Q2=70 kvar；换流站3的初始功率P3=-35 kW，Q3=50 kvar。直流侧电压、换流站电压允许范围设为0.9 pu≤U≤1.1 pu，滤波器的电纳Bf=0.088 7 pu，1-6、2-6支路阻抗为0.052 pu，2-3支路阻抗为0.052 pu，1-5、5-4、4-3支路阻抗为0.073 pu，给出的功率参数是实际值，其余均为标幺值。直流系统，交流系统以1 MVA为基值。采用C++语言编程，在VS2010进行测试，交流潮流收敛精度、直流潮流收敛精度、交替迭代收敛精度ε均设为0.000 1，在直流节点4，5，6处接入DC/DC变换器，分别为变换器1，2，3。变换器2，3变换的电压为10kV/6kV，二极管阻抗 0.001 3Ω，电感6mH，开关频率为300kHz。变换器1变换的电压为20kV/10kV，与风机连接，开关频率200kHz，风机额定功率为30kW，忽略风机的损耗。算例结合变换器和换流站各种控制方式，对以下几种情况进行了测试。

控制组合方式1：换流站1为平衡换流站，换流站2为P-U下垂控制，换流站3恒P控制，变换器2和3两端都为恒P控制，变换器1与风机相连一端采用恒U控制，另一端恒P控制。

控制组合方式2：换流站1和2均为U-P下垂控制，换流站3恒P控制，变换器2和3两端都为恒P控制，变换器1与风机相连一端采用恒U控制，另一端为U-I下垂控制。

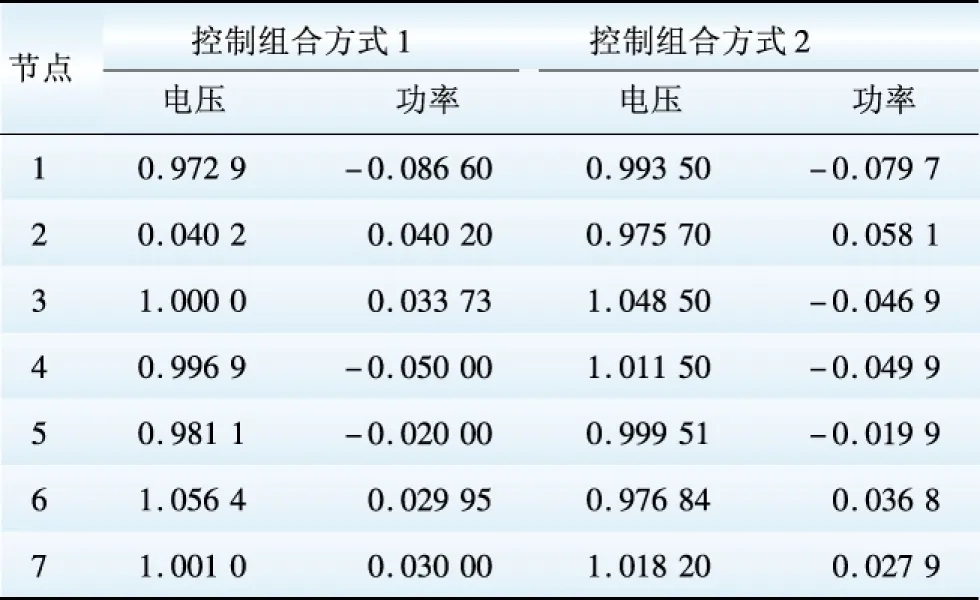
表2—4是通过不同换流站、变换器运行于不同组合控制方式下交直流迭代计算得到。限于篇幅关系，给出控制方式组合1仿真得到的交流节点电压标幺值，如表2所示。另外，表3—4是2种组合方式下仿真结果，表3是换流站注入功率标幺值，表4是直流节点电压标幺值和直流功率标幺值。以1 MVA为基值，交流侧选取69，24.9，4.16 kV作为电压基准值，直流侧选取20，10 kV作为电压基值，控制组合方式1和2，交直流相互之间交替迭代次数分别为3、4次，直流潮流均为3次迭代就可以收敛，程序具有良好的收敛性能，验证了所提算法的有效性和正确性。从潮流计算结果可以得到，不同控制方式下直流电网的潮流分布存在明显差异。另外对控制组合方式1的换流器、变换器、直流线路损耗进行了计算，换流站损耗50.39%，变换器30.28%,线路损耗19.33%，损耗数据表明，变换器的损耗不能够忽略不计。

表2 交流节点电压值
Table 2 Voltage of AC buses pu

图6 改进的IEEE 34节点算例Fig.6 Improved IEEE 34 node example

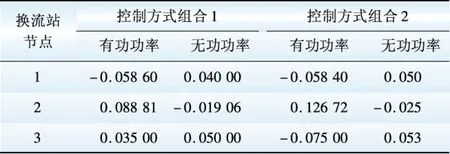
表4 直流节点电压值与功率值Table 4 Voltageof DC buses pu

6 结论

本文从VSC-MTDC和交流不平衡模型出发，建立了DC/DC换流器模型，修改了DC网络的雅可比矩阵，计及换流站和变换器各种控制方式，基于推导修正的雅可比矩阵，提出了一种适用于配电网交直流混合系统潮流的交替求解算法，最后通过改进的仿真算例，对改进型IEEE 34节点算例进行了仿真，结果表明程序收敛性能良好，同时还表明在进行交替迭代过程中，DC/DC变换器的损耗不能忽视。采用交替迭代潮流计算简单清晰，程序通用性好。易将上述算法扩充到多个AC和DC的配电网系统。

[1]叶李心， 江道灼，尹瑞，等. 直流配电实验系统初探[J].电力建设，2014，35(3)：49-53. YE Lixin，JIANG Daozhuo，YIN Rui，et al.Preliminary investigation on DC power distribution experimental system[J]. Electric Power Construction，2014，35(3)：49-53.

[2]BARADAR M, GHANDHARI M.Amulti-option unified power flow approach for hybrid AC/DC grids incorporating multi-terminalVSC-HVDC[J].IEEE Transactions on Power Systems，2013，28(3)：2376-2383.

[3]ARBOLEYA P,DIAZ G,COTO M. Unified AC/DC power flow for traction systems: A new concept[J]. IEEE Transactions on Vehicular Technology,2012,61(6):2421-2430.

[4]FENG W，TUAN L A，TJERNBERG L B，et al.A new approach for benefit evaluation of multiterminal VSC-HVDC using a proposed mixed AC/DC optimal power flow[J].IEEE Transactions on Power Delivery，2014，29(1)： 432-443.

[5]HAILESELASSIE T M，UHLEN K.Impact of DC line voltage droops on power flow of MTDC using droop control[J].IEEE Transactions on Power Systems，2012，27(3)：1441-1449.

[6]WANG W，BARNES M.Power flow algorithms for multi-terminal VSC-HVDC with droop control[J].IEEE Transactions on Power Systems，2014，29(4)： 1721-1730.

[7]王锡凡， 方万良，杜正春. 现代电力系统分析[M].北京：科学出版社，2003：186-187.

[8]袁旭峰，程时杰，文劲宇. 基于CSC和VSC的混合多端直流输电系统及其仿真[J]．电力系统自动化，2006，30(20)： 32-36． YUAN Xufeng，CHENG Shijie，WEN Jinyu. Simulation study for a hybrid multi-terminal HVDC system based on VSC and CSC[J].Automation of Electric Power Systems, 2006，30(20)：32-36．

[9]陈谦， 唐国庆，王浔.多端VSC-HVDC系统交直流潮流计算[J].电力自动化设备，2005，25(6)：1-6. CHEN Qian，TANG Guoqing，WANG Xun.AC-DC power flow algorithm for multi-terminal VSC-HVDC systems[J].Electric Power Automation Equipment，2005，25(6)：1-6.

[10]ANGELES-CAMACHO C，TORTELLI OL， ACHA E. Inclusion of a high voltage DC-voltage source converter model in a Newton-Raphson powerow algorithm[J].IEEE Proceedings-Generation， Transmission and Distribution，2003，150(6)：691-696.

[11]BEERTEN J，COLE S，BELMANS R. Generalized steady-state VSC MTDC model for sequential AC/DC power flow algorithms[J].IEEE Transaction on Power System，2012，27(2)：821-829.

[12]薛振宇， 房大中.基于双向迭代的交直流互联电力系统潮流计算[J].电力系统自动化，2013，37(5)：61-67. XUE Zhenyu，FANG Dazhong.A power flow calculation algorithm for AC/DCinterconnected power systems based on bi-directional iteration[J].Automation of Electric Power Systems，2013，37(5)：61-67.

[13]DUGAN R C，MCDERMOTT T E.Anopen source platform for collaboratingon smart grid research[C]// 2011 IEEE Power and Energy Society General Meeting. San Diego, CA : IEEE，2011:1-7.

[14]欧阳长莲. DC-DC开关变换器的建模分析与研究[D].南京：南京航空航天大学，2005. OUYANG Changlian.The study and modeling analysis for DC-DC switching converter[D].Nanjing：Nanjing University of Aeronautics and Astronautics，2005.

[15]BARRADO A，PLEITE J，LAZARO A，et al.Utilization of the power losses map in the design of DC/DC converters[C]//Power Electronics Specialists Conference.Fukuoka：IEEE，1998：1543-1547.

[16]PAWLAK M，RADOMSKI G，KAPLON A.Experimental verification of DC/DC boost converter calculation model considering conduction losses[C]//Selected Problems of Electrical Engineering and Electronics.Kielce：IEEE，2015：1-6.

[17]谷雨. 双向高效率DC-DC变换器的研究[D].哈尔滨：哈尔滨工业大学，2011. GU Yu.The research on high-efficiency bidirectional DC-DC converter[D].Haerbin：Harbin Institute of Technology，2011.

[18]赵成勇， 李路遥，翟晓萌，等.新型模块化高压大功率DC-DC变换器[J].电力系统自动化，2014，38(4)：72-75. ZHAO Chengyong，LI Luyao，ZHAI Xiaomeng，et al.A new of modular high-voltage high-power DC-DC converter[J].Automation of Electric Power Systems，2014，38(4)：72-75.

[19]PIZANO-MARTINEZ A, FUERTE-ESQUIVEL C R, AMBRIZ-PEREZ H, et al. Modeling of VSC-Based HVDC systems for a Newton-Raphson OPF algorithm[J]. IEEE Transactions on Power Systems, 2007, 22(4):1794-1803.

(编辑 蒋毅恒)

Power Flow Calculations for AC/DC Hybrid Distribution Network with Multi-Terminal DC

LIU Yaohua1,2,PEI Wei1, YANG Yanhong1, ZHAO Zhenxing1, DENG Wei1, YU Ting3, HUANG Renle4

(1.Institute of Electrical Engineering, Chinese Academy of Science, Beijing 100190, China;2.School of Electronic, Electrical and Communication Engineering,University of Chinese Academy of Sciences,Beijing 100190, China;3.China Electric Power Research Institute,Beijing 100192, China;4.State Grid Beijing Electric Power Company,Beijing 100031,China)

The traditional AC/DC power flow calculation method is mainly used for transmission network, but the AC /DC distribution network needs to consider many problems, such as three-phase unbalance on the AC side, low voltage multi-terminal DC (MTDC) access in to distributed generation on the DC side, and so on. To solve those problems, this paper proposes the MTDC power flow calculation sequential method for AC/DC hybriddistribution networkwith considering three-phase unbalance.Firstly, we construct the unbalanced three-phase model for AC system and converter station. Then,we derive DC power flow equation with considering different control modes of converter station. On this basis, we derive the modified equation for DC power flow calculation with DC/DC converter. According to different control modes for DC/DC converter and converter station, we propose the different equivalent solution ways for AC/DC power flow calculation. At last, an improved IEEE 34 node example is presented to verify the proposed algorithm. The simulation results show that the proposed power flowcalculation method of AC/DC distribution network for processing three-phase unbalance, distributed generation for DC and other problems has better convergence performance, under different control modes of MTDC.

multi-terminal DC; distribution network;compensating current; DC/DC converter; AC/DC sequential method

国家高技术研究发展计划项目(863计划)(2015AA050102)；国家自然科学基金项目(51507164)

TM 751

A

1000-7229(2016)05-0083-08

10.3969/j.issn.1000-7229.2016.05.016

2016-03-23

刘耀华(1989)，男，硕士，主要研究方向为交直流配电网运行技术与智能电网；

裴玮(1982)，男，博士，研究员，通信作者，主要从事含分布式能源的电力系统分析、微电网运行控制和智能电网的研究；

杨艳红(1985)，男，助理研究员，主要从事微电网、交直流配电网的计算分析与运行优化的研究；

赵振兴(1985)，男，硕士，助理研究员，主要研究方向分布式发电；

邓卫(1983)，男，博士，副研究员，主要研究方向为分布式能源运行控制技术；

于汀(1984)，男，博士，副研究员，主要从事电网调度技术研究；

黄仁乐(1963)，男，硕士，教授级高级工程师，长期从事电力系统自动化和电网技术的研究和管理工作。

Project supported by the National High Technology Research and the Development of China (863 Program) (2015AA050102), and the National Natural Science Foundation of China(51507164)