两部制电价机制下的发电权双边交易谈判模型
林昶咏, 文福拴,2, 蒙文川, 冷媛, 张翔, 宋艺航
(1. 浙江大学电气工程学院,杭州市 310027; 2. 文莱科技大学电机与电子工程系, 文莱斯里巴加湾 BE1410; 3. 南方电网科学研究院, 广州市 510080)
两部制电价机制下的发电权双边交易谈判模型
林昶咏1, 文福拴1,2, 蒙文川3, 冷媛3, 张翔3, 宋艺航3
(1. 浙江大学电气工程学院,杭州市 310027; 2. 文莱科技大学电机与电子工程系, 文莱斯里巴加湾 BE1410; 3. 南方电网科学研究院, 广州市 510080)
发电权交易有利于优化电源结构, 促进节能降耗。发电权交易可以通过集中竞价或双边谈判实现。针对基于双边谈判的发电权交易模式, 研究了两部制电价机制下的发电权双边交易谈判策略, 建立了基于贝叶斯模型的多目标谈判模型。首先, 提出了两部制电价机制下发电权买卖双方的交易效益计算模型; 然后, 利用贝叶斯学习模型逐步修正对谈判对象价格底线的估计, 并在此基础上综合考虑议题权重及最大风险度来确定新一轮报价, 通过多轮谈判后获得最终谈判价格;最后, 通过算例对所提出方法进行了说明。计算结果表明, 最终交易价格收敛于理论最优解附近, 且受谈判双方出价策略影响。
发电权; 两部制电价; 双边交易; 贝叶斯模型
0 引 言
发电权交易作为引导低能耗机组替代高能耗机组发电的重要手段, 有利于优化电源结构, 促进节能降耗, 因而在国内受到普遍重视。发电权交易指发电公司之间通过买卖交易方式交换计划发电量, 系建立在原有发电计划基础之上的再分配手段, 对电力系统内资源的合理配置具有重要意义。国家电力监管委员会于2008年3月颁布了《发电权交易监管暂行办法》, 标志着发电权交易进入了实施阶段。针对发电权交易的模式、模型、优化等方面, 国内学者开展了很多研究工作。
发电权交易模式主要包括集中竞价模式和双边交易模式两大类。文献[1]探讨了集中竞价模式的机理和相关理论问题, 分析了通过经纪人进行发电权交易的经济效益;文献[2]考虑了集中竞价过程中的成本损耗, 设计了一种激励相容的发电权交易模式;文献[3]分析了这2类交易模式的利弊, 并针对3种情况设计了发电权交易机制及价格测算方式。
发电权交易模式不同, 相关的交易模型也不同。文献[4]提出了集中竞价模式和双边交易模式的协调方法, 设计并比较了10种发电权交易模型;文献[5]基于期权理论构造了一种发电权双边交易模型;文献[6]基于利益相关者理论, 设计了一种能体现不同发电权交易商利益需求的发电权交易模型;文献[7]综合考虑了双边交易市场、月度和日前集中竞价市场, 建立了基于水火电置换的发电权调节市场, 并建立了置换电量在发电权交易主体中的优化分配模型。
在发电权交易优化方面, 现有文献主要针对与发电权相关的网损分配、阻塞调度、收益分配等方面展开研究。文献[8]在发电权交易中考虑了网损成本, 确定了网损成本与交易电量之间的关系, 并对集中竞价模式做了改进;文献[9]提出了以最大化社会效用、最大化成交量、考虑能耗约束的最大化成交量为目标函数的3种阻塞调度模型, 并对这3种模型进行了比较分析;文献[10]运用合作博弈理论中夏普利值法与核心法分析了发电权集中竞价交易中的利润分配结果, 以吸引更多机组参与发电权交易;文献[11]考虑了两部制电价机制下的发电权集中交易模式, 并给出了相应的计算模型。
发电权双边交易方面的研究主要是针对发电权交易双方的报价策略开展的。文献[12]基于Zeuthen决策与贝叶斯学习过程设计了一种发电权双边交易模型。该模型考虑了由于谈判双方无法准确把握对手信息而导致谈判破裂或在交易中承受不公平结果的情况, 通过采用多轮贝叶斯学习和Zeuthen策略来逐步获取对方成本信息, 进而推动谈判进展。算例仿真表明,采用该模型双方报价会逐步收敛, 有助于最终达成交易, 谈判效率较高。文献[13]研究了发电权双边交易的均衡问题, 利用静态不完全信息博弈中的贝叶斯纳什均衡定理,针对完全开放的发电权交易市场,建立了供需双方叫价拍卖不完全信息贝叶斯博弈模型,得到了供需双方的均衡报价策略, 并给出了交易流程。在该模型中, 买卖双方在使自身利益最大化的优化决策过程中考虑了交易成交概率。研究表明,当买卖双方均采用线性策略时, 得到的均衡状态的净剩余高于其他贝叶斯均衡状态, 该模型有利于最大化整体社会效益, 能够引导资源优化配置。
现有针对发电权交易的研究大多集中于集中竞价模式, 对于双边交易模式则研究较少。在此背景下,本文针对发电权双边交易模式, 在两部制电价机制下, 采用贝叶斯学习模型和合作博弈谈判理论, 构造发电权双边交易谈判模型, 研究买卖双方的策略学习过程及报价机制, 并对采用不同谈判策略时所获得的谈判结果进行分析。
1 基于两部制电价的发电权交易效益分析
1.1 容量电价效益分析
容量电价主要反映机组以投资成本为主的固定成本, 由政府依据不同发电机组的投资成本进行核准。新建机组一般为大容量、低能耗机组, 投资成本高, 还贷压力大, 其容量电价也相对较高。容量电价与实际发电量无关, 但在发电权交易过程中, 需要将容量电价按照机组的实际可用容量和可用小时数进行折算, 以实现与电量电价的同步结算。相关计算公式为[14]
(1)
式中:Pcon为折算后的容量电价;Ec为每年回收的总容量费用;Ea为机组可用容量;H为机组年可用小时数。
发电权交易实施后,由于发电权买方的实际发电量较计划发电量有所增加,如果按照原有的容量电价结算方式直接进行结算, 则买方折算后的容量电价Pcon将会降低; 另一方面,由于发电权卖方的实际发电量减小,卖方折算后的容量电价将会上升。同时, 发电权交易买方一般为大型机组, 建设成本高, 还贷压力大, 希望在容量电价市场中获得稳定收益来确保机组投资建设费用的回收; 而发电权交易卖方一般为小型机组或老旧机组, 基本已完成投资回收任务, 对容量电价市场收益需求相对较低。为保证发电权交易双方的公平性, 发电权卖方需根据折算的容量电价支付给买方一定的补偿费用, 用于弥补买方因发电权交易导致的损失, 该补偿费用即为发电权交易容量电价价格。在引入该补偿价格之后, 发电权买方的总容量电价获益即为卖方对买方的补偿费用; 发电权卖方的总容量电价获益即为卖方在支付给买方容量电价补偿费用之后的额外容量电价收益。这样, 买卖双方的容量电价收益分别为:
Rc,buy=pcΔQ-Fc,buyΔQ
(2)
Rc,sell=(Pc,sellQ0,sell-pcΔQ-Fc,sellΔQ)-
Pc,sell(Q0,sell-ΔQ)
(3)
式中:Rc,buy和Rc,sell分别表示发电权买卖双方的容量电价收益;pc表示发电权交易容量电价结算价格;ΔQ表示单位时间内发电权交易电量;Fc,buy和Fc,sell分别表示买卖双方单位发电权交易量在容量电价谈判过程中消耗的成本;Pc,sell表示卖方交易前折算后的容量电价;Q0,sell表示卖方交易前的初始发电量。
则买卖双方单位发电权交易量的容量电价收益Vc,buy和Vc,sell分别为:
(4)
(5)
式(4)和式(5)中除pc外, 其余参数均为定值。这样, 发电权交易过程中买卖双方的单位发电权交易量的容量电价收益是关于pc的线性函数。买卖双方的容量电价价格底线Bc,buy与Bc,sell分别为:
Bc,buy=Fc,buy
(6)
Bc,sell=Pc,sell-Fc,sell
(7)
1.2 电量电价效益分析
电量电价主要反映机组的变动成本。以燃煤火电机组为例, 变动成本主要指燃料费。燃煤机组的发电成本与发电量之间一般采用二次函数表示[15]:
C(Q)=aQ2+bQ+c
(8)
式中a、b、c为燃煤机组的煤耗或成本系数。
根据燃煤机组的煤耗特性函数可知, 当机组进行发电权交易时, 假设单位时间内发电权交易量为ΔQ, 则买卖双方的发电燃煤成本变化量分别为:
ΔCbuy=C(Q0,buy+ΔQ)-C(Q0,buy)= (abuyΔQ+2abuyQ0,buy+bbuy)ΔQ
(9)
ΔCsell=C(Q0,sell-ΔQ)-C(Q0,sell)= (asellΔQ-2asellQ0,sell-bsell)ΔQ
(10)
在交易过程中, 买方和卖方从电量电价中获得的收益Re,buy和Re,sell分别为[12]:
Re,buy=peΔQ-ΔCbuy-Pe,buyΔQ-Fe,buyΔQ=
(pe-Pe,buy-2abuyQ0,buy-abuyΔQ-bbuy-Fe,buy)ΔQ
(11)
Re,sell=Pe,sellΔQ-ΔCsell-peΔQ-Fe,sellΔQ=
(Pe,sell-pe+2asellQ0,sell-asellΔQ+bsell-Fe,sell)ΔQ
(12)
式中:Re,buy和Re,sell分别表示发电权买卖双方的电量电价收益;pe表示发电权交易电量电价结算价格;Fe,buy和Fe,sell分别表示买卖双方单位发电权交易量的电量电价在谈判过程中消耗的成本;Pe,buy和Pe,sell分别表示买卖双方的上网电量电价。
则买卖双方单位发电权交易量的电量电价收益Ve,buy和Ve,sell分别为:
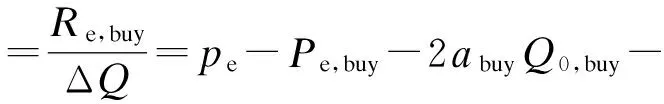
(13)

(14)
若买卖双方的发电权交易量是确定的, 则式(13)和式(14)中除pe外, 其余参数均为定值。这样, 发电权交易过程中买卖双方的单位发电权交易量的电量电价收益是关于pe的线性函数。买卖双方的电量电价价格底线Be,buy与Be,sell分别为:
Be,buy=Pe,buy+2abuyQ0,buy+abuyΔQ+bbuy+Fe,buy
(15)
Be,sell=Pe,sell+2asellQ0,sell-asellΔQ+bsell-Fe,sell
(16)
在发电权交易过程中, 双方均应处于盈利状态, 否则谈判无法达成。这样, 发电权交易最终成交时应满足下述约束:
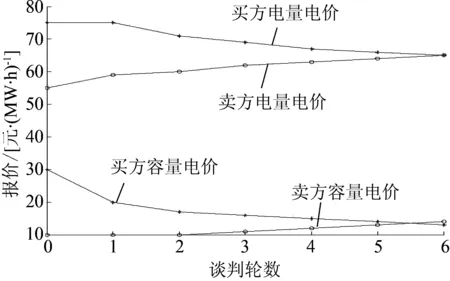
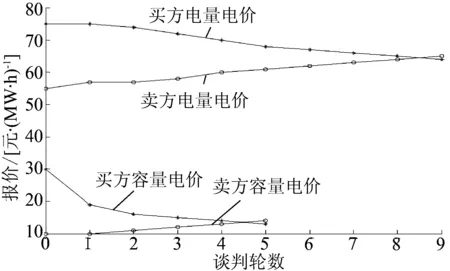
Bc,buy+Be,buy (17) 2.1 贝叶斯学习模型 贝叶斯学习模型运用贝叶斯统计实现概率预测, 基于贝叶斯公式利用所获得的信息对学习对象的先验知识进行修正, 从而更准确地获得预测信息。 贝叶斯公式可以表述为: 存在与事件H有关的一组事件A1,A2,…,An, 满足[16]: (1)P(Ai)>0; (2)Ai∩Aj=φ,i≠j; (3)∪(Ai)=Ω。 则贝叶斯公式定义为 (18) 式中:P(Ai)为先验概率, 表示在贝叶斯学习前对学习对象的先验知识;P(Ai|H)为后验概率, 表示经过贝叶斯学习修正后对学习对象的认识;P(H|Ai)为条件概率, 表示事件Ai发生的条件下事件H发生的概率。 2.2 发电权买卖双方的贝叶斯学习模型 在发电权双边交易谈判过程中, 发电权买卖双方准确知道自身容量电价与电量电价的价格底线, 但不知道对方的价格底线从而需要估计, 这些估计值即为贝叶斯学习模型的先验知识, 双方在谈判过程中的报价可通过贝叶斯学习模型进行修正。发电权交易双方都有动机通过改善对对方价格底线的估计值来获得在谈判过程中的优势地位。 现在从买方角度分析容量电价的贝叶斯学习过程。设卖方交易的容量电价价格底线为B, 将买方对卖方容量电价价格底线的估计值分为I个区间, 即买方估计卖方有I个价格底线区间, 第i个容量电价价格底线估计区间为Bi(i=1,2,…,I), 且假设在每个Bi区间内的价格底线服从均匀分布。对应每个Bi, 买方进一步将估计的卖方容量电价报价分为J个区间, 卖方报价属于第j个容量电价报价区间的概率为pi,j(j=1,2,…,J)。谈判开始前, 买方对卖方容量电价交易底线的期望为 (19) 当发电权卖方报价后, 买方基于卖方报价利用贝叶斯公式对原先估计的卖方报价区间的概率分布情况进行修正, 即发电权买方对卖方的贝叶斯学习模型为 (20) 修正后的买方对卖方容量电价交易底线的估计值的均值为 (21) 式(20)和式(21)为经过修正后买方对卖方容量电价报价分布概率和期望的估计, 即为下一轮谈判中的贝叶斯学习的先验知识。在卖方更新容量报价后, 买方对卖方容量电价底线估计的均值进行修正, 经过多轮谈判后买方的估计逐渐逼近卖方的容量电价底线。 在贝叶斯学习过程中, 买卖双方分别按照对方报价情况调整自身对对方价格底线区间的概率分布的估计。上述学习模型可用于发电权买卖双方对对方容量电价和电量电价的学习与估计。 3.1 两部制电价下发电公司收益的最大风险度 最大风险度反映发电公司的收益风险情况。最大风险度越高, 则发电公司在最终拍卖成交时利益受损的可能性就越大。在发电权交易谈判过程中, 发电公司不仅要计算己方的最大风险度, 还需要估计对方的最大风险度以分析对方的报价策略, 再根据己方及估计的对方最大风险度确定谈判策略。 定义发电权买卖双方在两部制电价机制下的最大风险度分别为: (22) (23) (24) (25) 式中:rc,buy、re,buy、rc,sell和re,sell分别表示发电权买方容量电价风险度、买方电量电价风险度、卖方容量电价风险度、卖方电量电价风险度;pc,buy、pe,buy、pc,sell和pe,sell分别表示买方容量电价报价、买方电量电价报价、卖方容量电价报价和卖方电量电价报价。 对于发电权买方, 其容量电价、电量电价的收益函数可以通过式(4)和式(13)求得精确函数表达式, 但其对卖方容量电价、电量电价的收益需要通过贝叶斯学习模型去不断修正对卖方报价底线的估计来得到, 进而用估计的收益函数估计卖方最大风险度。在收益函数确定的情况下, 最大风险度r的取值范围在[0,1]之间。然而, 由于谈判过程中买方无法获知卖方精确的价格底线及收益函数, 在谈判初期买方对卖方的初始价格底线估计可能与卖方的实际价格底线有较大偏差, 这样就可能出现卖方收益估计值为负的情况, 即r可能会在谈判初期大于1。随着谈判的进行, 买方逐步修正对卖方价格底线的估计,r的取值就局限于[0,1]之间。对于发电权卖方, 情况类似。 3.2 两部制电价机制下的最小谈判让步幅度 在发电权交易谈判过程中, 买卖双方都会根据当前双方报价情况计算己方容量电价和电量电价的最大风险度, 同时根据先验知识估计对方容量电价和电量电价的最大风险度。当计算出己方最大风险度低于对方时, 为了让谈判进行下去, 己方可以做出些让步, 以诱导对方进一步报价, 促使谈判朝收敛方向推进。如果计算出己方最大风险度高于对方, 则保留原报价, 等待对方做出让步, 以保证己方权益不受损失。双方在谈判过程中采用贝叶斯学习模型不断修正对谈判对象价格底线的估计, 进而更新对谈判对象收益函数的估计; 如此循环, 引导谈判逐步收敛到最终交易价格。 由于在两部制电价机制下针对发电权交易的双边谈判过程需针对容量电价和电量电价分别进行谈判, 故引入权重因子φ(0<φ<1), 用于描述不同谈判方对不同议题的重视程度。谈判权重因子越大, 则谈判方对该议题重视程度越高, 参与谈判的发电公司越希望通过放慢谈判速度来逐步试探对方价格底线, 以获得更好的谈判结果。采用4个权重因子φc,buy、φe,buy、φc,sell、φe,sell分别表示买方容量电价、电量电价谈判的权重和卖方容量电价、电量电价谈判的权重, 且满足如下约束: (26) 此外, 引入让步因子k(0≤k≤1), 用于描述谈判方在谈判过程中的让步速度及谈判的收敛速度。k值越大, 则谈判中双方的让步速度越慢。对买卖双方的谈判过程设定统一的k值, 其受谈判时间、谈判出价轮数限制, 用于调节全局谈判速度, 与买卖双方采取的谈判策略无关。 (27) 在此轮谈判中, 买方的最小让步幅度为 (28) 3.3 两部制电价机制下的发电权双边交易谈判流程 在两部制电价机制下的发电权双边交易谈判过程中, 容量电价和电量电价的谈判同步进行, 待容量电价与电量电价谈判结果分别收敛到一个最终价格时, 谈判结束, 双方发电权交易成功。若其中任意一项谈判不能收敛到双方认同的价格或谈判轮数超出给定值, 则谈判失败。谈判具体流程如下: (1)双边基于自身价格底线, 提交容量电价和电量电价的初始报价; (2)根据对方报价, 修正对谈判对象价格底线的估计值及报价分布; (3)计算最大风险度, 选择让步或保留原报价; (4)提交新一轮报价, 检验谈判是否收敛, 如谈判收敛, 则谈判成功, 谈判过程结束; 若谈判不收敛, 且在允许谈判轮数内, 则返回步骤(2), 否则谈判失败; (5)确认发电权交易结果; (6)根据最终谈判结果签署发电权交易合同。 给定参与发电权交易的买卖双方在单位时间内发电权交易量为100 MW·h。买卖双方初始报价如下: 买方容量电价报价为30元/(MW·h), 电量电价报价为75元/(MW·h); 卖方容量电价报价为10元/(MW·h), 电量电价报价为55元/(MW·h)。 需要指出, 本文中所讲的买方与卖方是针对“发电权”的买卖进行, 与一般的商品买卖关系不同。发电权的买方是替代发电的大机组, 购买发电权后进行发电; 发电权的卖方是被替代发电的小机组, 发电量转让给了买方。在最终结算时, 发电权的卖方付钱给买方, 所以卖方希望支付的费用越少越好, 而买方希望获得的收益越大越好。发电权的买方应该理解为电量的卖方, 相当于多发电卖给小机组。 买卖双方发电机组相关参数如表1所示[12]。设定允许的谈判最多轮次为15, 市场让步因子k为0.5。 表1 机组参数 4.1 容量电价谈判过程 4.1.1 买方谈判过程 买方根据对卖方的先验知识, 对卖方的容量电价价格底线的分布概率及报价概率进行估计。给定买方对卖方的价格底线分布概率估计如表2所示。 表2 买方对卖方容量电价价格底线分布概率的估计 在不同的容量价格底线水平下, 卖方的报价策略一般也不同。不同容量电价价格底线水平下的卖方报价策略如表3所示。 表3 买方对不同容量电价价格底线下卖方报价策略的估计 元·(MW·h)-1 在谈判开始时, 买方首先根据买方的先验知识对卖方的容量电价价格底线进行估计。根据表2的先验知识及式(19), 可以获得买方对卖方容量电价价格底线的估计值为25元/(MW·h)。根据式(6)计算得知买方的容量电价价格底线为0.5元/(MW·h)。发电权买方获得的容量电价收益实质上为卖方对发电权买方损失的折算容量电价的补偿, 该部分电价买方并无其他成本, 故价格底线较低。 在买方获知卖方容量电价报价为10元/(MW·h)后, 根据贝叶斯公式及表3, 对卖方的容量电价价格底线估计进行修正, 获得新的卖方价格底线分布期望, 更新表2数据, 同时根据式(19)将对卖方的价格底线估计值调整为25.10元/(MW·h)。 进一步, 买方根据己方价格底线及估计的卖方价格底线, 求得买卖双方的容量电价最大风险度分别为0.678 0和1.324 2。假设买方对发电权交易的容量电价与电量电价重视程度相同, 即买方的谈判权重因子φc,buy=φe,buy=0.5, 此时买方的最大风险度小于卖方, 即rc,buy<(1-φc,buy+k)rc,sell, 故买方根据让步策略需要做出主动让步。根据式(27)可以计算出买方第2阶段报价为20元/(MW·h), 即该轮谈判中买方的让步幅度Δpc,buy=10元/(MW·h)。买方在降低己方报价后, 等待卖方下一步行动。在卖方新一轮报价之后, 买方再重复上述过程并做出决策, 直至谈判成功或达到限制轮数为止。 4.1.2 卖方谈判过程 与买方的谈判过程类似, 卖方对买方的容量电价价格底线分布概率进行估计, 如表4所示。 在不同容量电价价格底线水平下的买方的报价策略如表5所示。 表4 卖方对买方容量电价价格底线分布概率的估计 表5 卖方对不同容量电价价格底线下买方报价策略的估计Table 5 Seller’s estimation of strategy of buyer’s offers over different acceptably lowest capacity prices 元·(MW·h)-1 根据表4的先验知识和式(19), 可计算出卖方对买方容量电价价格底线的估计值为1.1元/(MW·h), 根据式(7)可求得卖方的容量电价价格底线为27.5元/(MW·h)。在买方提出其容量电价报价为30元/(MW·h)后, 卖方根据表5内容进行贝叶斯学习, 修正得到卖方新的价格底线为1.14元/(MW·h)。 同样假设卖方对发电权容量电价和电量电价的重视程度相同, 即卖方的谈判权重因子φc,sell=φe,sell=0.5。卖方根据己方价格底线及估计的买方价格底线, 求得买卖双方的容量电价最大风险度分别为0.692 9和1.142 9, 此时己方容量电价的加权最大风险度大于买方, 即rc,sell>(1-φc,sell+k)rc,buy, 故卖方选择保留原报价, 等待买方做出让步。在买方做出新一轮报价后, 卖方重复上述过程并做出决策, 直至谈判成功或达到限制轮数为止。 4.2 电量电价谈判过程 与容量电价谈判过程类似, 在电量电价谈判过程中, 买卖双方分别就对方的电量电价价格底线和报价概率进行估计, 结果如表6—9所示。 表6 买方对卖方电量电价价格底线分布概率的估计 表7 买方对不同电量电价价格底线下卖方报价策略的估计Table 7 Buyer’s estimation of strategy of seller’s offers over different acceptably lowest energy prices 元·(MW·h)-1 表8 卖方对买方电量电价价格底线分布概率的估计Table 8 Seller’s estimation of probability distribution of buyer’s acceptably lowest energy price 表9 卖方对于不同电量电价价格底线下买方报价策略的估计Table 9 Seller’s estimation of strategy of buyer’s offers over different acceptably lowest energy prices 元·(MW·h)-1 买卖双方分别根据己方的先验知识及对方报价情况进行贝叶斯学习, 修正对对方电量电价价格底线的估计值, 并计算双方最大风险度; 之后通过比较最大风险度决定己方谈判策略, 并重复这一过程直至谈判结束。 4.3 不同策略对交易谈判结果的影响分析 (1) 买卖双方对容量电价和电量电价同等重视 当买卖双方对容量电价和电量电价同等重视时,φc,buy=φe,buy=0.5,φc,sell=φe,sell=0.5, 此时买卖双方的报价收敛速度一致, 如图1所示; 2个电价谈判均需要6次才能达成最终交易, 最终成交的容量电价和电量电价价格分别为13.5元/(MW·h)和65元/(MW·h)。此时,买方和卖方容量电价收益分别为13元/(MW·h)和14元/(MW·h),电量电价收益分别为12.5元/(MW·h)和14.26元/(MW·h)。 图1 双方对容量电价和电量电价同等重视情况下的谈判过程Fig.1 Negotiation process for situation with equal weights on capacity price and energy price from both buyer and seller (2) 买卖双方均更重视电量电价 对于买卖双方均更重视电量电价的情形, 给定双方权重因子分别为φc,buy=φc,sell=0.4,φe,buy=φe,sell=0.6, 此时容量电价谈判让步幅度大, 收敛速度较快; 电量电价市场谈判出价谨慎, 让步幅度小, 收敛速度较慢, 如图2所示。最终, 容量电价谈判仅需5轮就结束, 而电量电价谈判需9轮谈判才收敛。观察电量电价谈判曲线可以发现, 在进行最后一轮报价时, 买方的电量电价报价比卖方的低, 此时双方报价虽未收敛到同一价格, 但已满足交易成交条件。给定此情况下最终成交价格为买方报价与卖方报价的平均值。这样, 最终成交的容量电价与电量电价价格分别为13.5元/(MW·h)与64.5元/(MW·h)。此时, 买方容量和电量电价收益分别为13元/(MW·h)和12元/(MW·h), 而卖方容量和电量电价收益分别为14元/(MW·h)和14.76元/(MW·h)。 图2 双方均更重视电量电价情况下的谈判过程Fig.2 Negotiation process for situation with a larger weight on energy price from both buyer and seller (3) 买方和卖方分别更重视电量电价和容量电价 对于买方和卖方分别更重视电量电价和容量电价的情形, 给定双方权重因子分别为φc,buy=0.4,φe,buy=0.6,φc,sell=0.6,φe,sell=0.4。此时, 买方在电量电价交易谈判时让步幅度较小, 在容量电价交易谈判时让步幅度较大, 而卖方则正好相反。如图3所示。此时, 最终成交的容量电价和电量电价价格分别为13元/(MW·h)和66元/(MW·h); 买方的容量和电量电价收益分别为12.5元/(MW·h)和13.5元/(MW·h); 卖方的容量和电量电价收益分别为14.5元/(MW·h)和13.26元/(MW·h)。由于买方的电量电价的权重因子更大, 其在电量电价交易中获得了更高的收益, 但在容量电价交易中获得的收益有所下降。 图3 买方和卖方分别更重视电量电价和容量电价情况下双方谈判过程Fig.3 Negotiation process for situation with a larger weight on energy price from buyer and a larger weight on capacity price from seller 4.4 谈判模型效用分析 在该算例中, 发电权买卖双方的容量电价价格底线分别为0.5元/(MW·h)和27.5元/(MW·h), 电量电价价格底线分别为52.5元/(MW·h)和79.26元/(MW·h)。就谈判双方的总体效益最优和双边交易的公平性问题, 可在纳什谈判解的合作博弈理论框架下进行分析。具体地, 当谈判双方谈判能力相同时, 实现双方总体效益水平最大化的成交价格应满足纳什福利函数[17]: max[Vc,buy(pc)+Ve,buy(pe)][Vc,sell(pc)+Ve,sell(pe)] (29) 在完全信息情况下, 根据买卖双方容量电价与电量电价价格底线, 可得到容量电价和电量电价的全局最优成交价格分别为14元/(MW·h)和65.88元/(MW·h), 对应的纳什福利函数最大值为722.53。事实上, 由于买卖双方无法准确获知对方的价格底线, 只能通过谈判逐步接近最优结果。谈判成交电价越接近全局最优成交价格, 谈判效率就越高。4.3节中描述的3种情形下的谈判结果的纳什福利函数分别为720.63、719.00和721.76, 均与最优解相当接近。这说明本文所设计的基于两部制电价的发电权双边交易谈判模型的最终成交价格都在最优成交价格附近, 且最终谈判结果受谈判双方出价策略的影响, 从而可以引导买卖双方在两部制电价机制下合理进行谈判决策, 谈判效率较高。 在两部制电价机制下, 构建了发电权双边交易谈判模型, 通过采用加权谈判方式对容量电价和电量电价展开同步谈判, 并利用贝叶斯学习模型更新对谈判对象价格底线的估计, 为买卖双方构造了一种可行的谈判策略。算例结果表明, 权重因子对谈判进程具有引导作用, 权重因子越大, 最终谈判收益越高, 但谈判时间也越长; 买卖双方可以逐步修正对谈判对象价格底线的估计, 谈判效率较高。 本文描述的引入谈判因子的谈判方法为在两部制电价机制下的发电权双边交易谈判研究提供了新的思路, 但研究工作还比较初步。下一步将扩展本文的研究工作, 包括用连续概率分布来模拟买卖双方对谈判对象容量电价和电量电价的价格底线估计, 在谈判过程中同时对价格底线和报价策略进行估计等。 [1]黎灿兵, 康重庆, 夏清, 等. 发电权交易及其机理分析[J]. 电力系统自动化, 2003, 27(6): 13-18. LI Canbin, KANG Chongqing, XIA Qin, et al. Generation rights trade and its mechanism[J]. Automation of Electric Power Systems, 2003, 27(6): 13-18. [2]王雅娟, 王先甲. 一种激励相容的发电权交易双边拍卖机制[J]. 电力系统自动化, 2009, 33(22): 25-28. WANG Yajuan, WANG Xianjia. An incentive compatible double auction mechanism of generation rights trade[J]. Automation of Electric Power Systems, 2009, 33(22): 25-28. [3]张森林, 孙延明, 张尧. 南方电力市场省间合约转让与置换交易机制研究[J]. 电网技术, 2012, 36(12): 262-268. ZHANG Senglin, SUN Yanming, ZHANG Yao. Research on mechanism of inter-provincial contract transfer and replacement transaction in south China electricity market[J]. Power System Technology, 2012, 36(12): 262-268. [4]尚金成. 基于节能减排的发电权交易理论及应用: (一)发电权交易理论[J]. 电力系统自动化, 2009, 33(12): 46-52. SHANG Jincheng. Generation right trade theory and its applications based on energy-saving and emission-reducing: part one generation right trade theory[J]. Automation of Electric Power Systems, 2009, 33(12): 46-52. [5]姚建刚, 周启亮, 张佳启, 等. 基于期权理论的发电权交易模型[J]. 中国电机工程学报, 2005, 25(21): 76-81. YAO Jiangang, ZHOU Qiliang, ZHANG Jiaqi, et al. Generation rights trade mode based on option theory[J]. Proceedings of the CSEE, 2005, 25(21): 76-81. [6]田帅. 基于利益相关者理论的发电权交易模式及其竞价策略[J]. 电力建设, 2014, 35(1): 122-126. TIAN Shuai. Generation rights trading model and bidding strategy based on stakeholder theory[J]. Electric Power Construction, 2014, 35(1): 122-126. [7]王雁凌, 张粒子, 杨以涵. 基于水火电置换的发电权调节市场[J]. 中国电机工程学报, 2006, 26(5): 131-136. WANG Yanling, ZHANG Lizi, YANG Yihan. Adjusting market of generation rights based on hydro-thermal exchange[J]. Proceedings of the CSEE, 2006, 26(5): 131-136. [8]黄大为, 刘志向, 杨春雨, 等. 计及网损成本的发电权交易模式[J]. 电力系统自动化, 2010, 34(5): 38-42. HANG Dawei, LIU Zhixiang, YANG Chunyu, et al. Generation right trading model considering transmission losses cost[J]. Automation of Electric Power Systems, 2010, 34(5): 38-42. [9]肖健, 文福拴. 发电权交易的阻塞调度[J]. 电力系统自动化, 2008, 32(18): 24-29. XIAO Jian, WEN Fushuan. Congestion dispatch for generation rights trade[J]. Automation of Electric Power Systems, 2008, 32(18): 24-29. [10]李莉, 丁亚伟, 谭忠富, 等. 发电权交易机制下基于合作博弈的利润分配模型[J]. 华东电力, 2009, 37(11): 1803-1806. LI Li, DING Yawei, TAN Zhongfu, et al. Profit distribution models based on game theory under power generation right trading mechanism[J]. East China Electric Power, 2009, 37(11): 1803-1806. [11]伍玉林, 文福拴, 丁剑鹰, 等. 基于两部制电价的发电权交易模式[J]. 华北电力大学学报, 2010, 37(5): 16-22. WU Yulin, WEN Fushuan, DING Jianying, et al. A two-part electricity price based generation-right trading mechanism[J]. Journal of North China Electric Power University, 2010, 37(5): 16-22. [12]宋艺航, 唐晓瑭, 张会娟, 等. 基于Zeuthen决策与贝叶斯学习的发电权双边交易模型[J]. 电力系统自动化, 2013, 37(11): 51-57. SONG Yihang, TANG Xiaotang, ZHANG Huijuan, et al. A generation rights bilateral trade model based on Zeuthen strategy and Bayesian learning[J]. Automation of Electric Power Systems, 2013, 37(11): 51-57. [13]廖屹. 基于博弈理论的发电权交易研究[D]. 成都: 西南交通大学, 2008. LIAO Yi. Study on a generation rights trade based on game theory[D]. Chengdu: Southwest Jiaotong University, 2008. [14]金明成, 金福国, 张健男. 浅谈两部制电价[J]. 东北电力技术, 2006, 27(8): 30-32. JIN Mingcheng, JIN Fuguo, ZHANG Jiannan. A brief introduction of double-system electricity price[J]. Northeast Electric Power Technology, 2006, 27(8): 30-32. [15]徐帆, 姚建国, 耿建, 等. 机组耗量特性的混合整数模型建立与分析[J]. 电力系统自动化, 2010, 34(10): 45-50. XU Fan, YAO Jianguo, GENG Jian, et al. Modeling and analysis of unit I/O characteristics based on mixed-integer programming[J]. Automation of Electric Power Systems, 2010, 34(10): 45-50. [16]谭忠富, 李莉, 王成文. 迭代竞价机制下发电商的贝叶斯学习模型[J]. 中国电机工程学报, 2008, 28(25): 118-124. TAN Zhongfu, LI Li, WANG Chengwen. Generations’ Bayesian learning model under iterative bidding mechanism[J]. Proceedings of the CSEE, 2008, 28(25): 118-124. [17]蒋国华. 基于博弈模型的智能电网需求响应管理及定价策略[D]. 杭州: 浙江工业大学, 2013. JIANG Guohua. Game theory model based demand response management and pricing strategy in smart grid[D]. Hangzhou: Zhejiang University of Technology, 2013. 林昶咏 (1992), 男, 硕士研究生, 主要从事电力经济与电力市场、智能电网等方面的研究工作; 文福拴 (1965), 男, 教授, 博士生导师, 通信作者, 主要从事电力系统故障诊断与系统恢复、电力经济与电力市场、智能电网与电动汽车等方面的研究工作; 蒙文川 (1976), 男, 博士, 高级工程师, 主要从事电力网络规划、能源经济等方面的研究工作; 冷媛 (1986), 女, 硕士, 工程师, 主要从事电力供需、能源电力发展领域研究工作; 张翔 (1988), 男, 硕士, 助理研究员, 主要从事能源经济、电力系统规划领域研究工作; 宋艺航 (1986), 男, 博士, 经济师, 主要从事电力能源经济领域研究工作。 (编辑 张小飞) Generation-Right Bilateral Transaction Negotiation Model Based on Two-Part Electricity Price LIN Changyong1, WEN Fushuan1,2, MENG Wenchuan3, LENG Yuan3, ZHANG Xiang3, SONG Yihang3 (1. School of Electrical Engineering, Zhejiang University, Hangzhou 310027, China;2. Department of Electrical and Electronic Engineering, Institut Teknologi Brunei, Bandar Seri Begawan BE1410, Brunei;3. Electric Power Research Institute, China Southern Power Gird, Guangzhou 510080, China) Generation-right trade is beneficial to optimize power structure and promote energy saving and consumption reduction, which can be implemented by centralized price bidding or bilateral negotiation. According to the generation-right trade mode based on bilateral negotiation, this paper studies the negotiation strategy of generation-right bilateral transaction based on two-part electricity price mechanism, and constructs the multiple-objective negotiation model based on Bayesian model. Firstly, we present the calculation model of trading benefits for both sides participating in generation-right trade based on two-part electricity price mechanism. Then, we adopt the Bayesian learning model to gradually improve the estimation of the opponent’s base price. On this basis, we comprehensively consider the weights of issues and the greatest risk degree to determine the bidding price in next round. After several rounds of negotiations, the final settlement price can be determined. Finally, the proposed method is demonstrated through example, whose results show that the settlement price is converged to the theoretical optimal solution, and dependent on the bidding strategies of both sides. generation-right; two-part electricity price; bilateral transaction; Bayesian model 国家重点基础研究发展计划项目(973项目)(2013CB228202);南方电网科学研究院科研项目(CSGTRC-K153018) TM 61; F416.6 A 1000-7229(2016)03-0090-09 10.3969/j.issn.1000-7229.2016.03.014 2015-12-24 Project supported by the National Basic Research Program of China (973 Program) (2013CB228202)2 发电权双边交易的贝叶斯学习模型
3 基于两部制电价的发电权交易谈判模型

4 算例分析
Table 1 Parameters of units
Table 2 Buyer’s estimation of probability distribution of seller’s acceptably lowest capacity price
Table 3 Buyer’s estimation of strategy of seller’s offers over different acceptably lowest capacity prices
Table 4 Seller’s estimation of probability distribution of buyer’s acceptably lowest capacity price
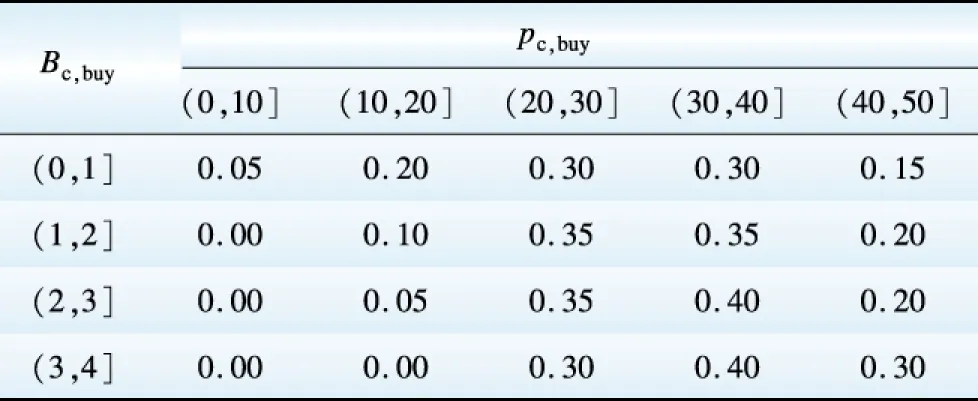
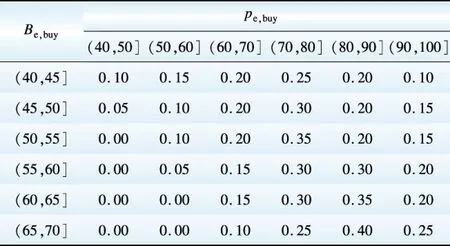
Table 6 Buyer’s estimation of probability distribution of seller’s acceptably lowest energy prices



5 结 语

