考虑源荷不确定性的概率最优潮流

代景龙，白晓清，鲍海波

(广西电力系统最优化与节能技术重点实验室(广西大学)，广西南宁　530004)

Probabilistic Optimal Power Flow by Considering the Uncertainty of Source and Demand Side DAI Jinglong, BAI Xiaoqing, BAO Haibo

(Guangxi Power System Optimization and Energy-saving Technique Key Lab, Guangxi University, Nanning 530004,China)



考虑源荷不确定性的概率最优潮流

代景龙，白晓清，鲍海波

(广西电力系统最优化与节能技术重点实验室(广西大学)，广西南宁530004)

Probabilistic Optimal Power Flow by Considering the Uncertainty of Source and Demand Side DAI Jinglong, BAI Xiaoqing, BAO Haibo

(Guangxi Power System Optimization and Energy-saving Technique Key Lab, Guangxi University, Nanning 530004,China)

0引言

为更加可靠、全面地评估系统的线路安全情况、电压水平、市场运营的成本及盈利情况，新的电力市场优化模型与计算方法应该能够合理计及新能源出力、负荷功率和发电商报价的不确定特征。概率最优潮流[1]是在已知系统中影响优化计算的主要不确定变量概率分布的基础上，经过采样、优化、变换等步骤，获取系统运行特征量(目标函数，发电机有功、无功出力，电压，线路功率等)的统计信息。

目前概率最优潮流的研究领域涉及电压稳定的概率评估[2]、电力市场[1-3]、风电随机变量的最优场景[4]和风电能力分析[5]等；研究的方法主要有蒙特卡洛模拟[6-7](Monte Carlo simulation, MCS)法、点估计法[8-9]、解析法[10]、半不变量法[11-12]等。MCS从已知的概率分布中对随机变量进行模拟抽样，但较大的模拟次数要求严重限制了其工程应用；点估计法采用随机变量的高阶矩构造估计样本，是一种求解效果较好的方法，在电力市场的概率最优潮流计算中已有一定应用[8]；解析法线性化的过程将降低其计算精度，且随着变量的增大其计算量迅速增长，故难以处理复杂问题；半不变量法求解速度虽然很快，但文献[8]指出其需要从对数障碍函数内点法中提取二阶海森矩阵，计算较为复杂。

无迹变换(unscented transformation, UT)[13-15]方法处理概率分析问题速度快、精度高，无需正交变换或Nataf变换即可高效处理随机变量相关性。它不仅克服了MCS需要大量模拟样本、解析法计算量指数增加以及半不变量法计算相对复杂的缺点，而且具有与2n+1采样规模的三点估计法基本相当的计算精度。

本文考虑新能源出力、负荷功率、发电厂商报价的不确定性，建立了电力市场的概率最优潮流模型，并采用对称采样策略的UT结合现代内点法[16]求解系统运行特性的概率特征。其中，UT方法中不仅引入了比例及高阶信息参数以减小局部效应及高阶项误差，而且考虑了变量相关性的影响。IEEE30和118节点系统计算结果表明：与MCS的结果相比，UT方法实现简单，可高效求得系统运行特征量的概率信息。

1计算模型

1.1电力市场的优化模型

考虑潮流方程约束、发电机容量约束、电压幅值约束、线路传输功率约束，以市场收益R(PGi,PDi)最大化为目标，构建概率最优潮流计算模型：

(1)

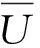
式(1)的电力市场优化模型是确定性的，现将风电出力、光伏发电系统出力、发电商报价以及负荷功率不确定性考虑到上述模型中，则式(1)就转变为发电侧开放竞价市场的概率最优潮流模型。

1.2风、光、荷、发电商报价的概率模型

风力发电和光伏发电的出力主要取决于风速和光照强度，然而风速和光照强度具有较强的波动性，分别采用典型的Weibull和Beta[17]分布概率模型对风速和光照强度建模。概率密度函数：

(2)

(3)

式中:v为风速；K和C分别为Weibull分布的形状参数和尺度参数；r、rmax分别为实际和最大辐照度，W/m2；α、β为Beta分布的形状参数；Γ为Gamma函数。

风力发电机组、光伏发电系统的出力分别为

(4)

(5)

式中：PWT为风电机组的实际输出功率；vin和vout分别为切入风速和切出风速；vr为额定风速；Pr为风电机组的额定输出功率；k1=Prvin/(vin-vr)和k2=Pr/(vr-vin)为常数；PPV为光伏发电系统的出力；A为光伏阵列总面积；η为光电转换效率。

假设风电和光伏发电恒功率因数运行，则两者的无功功率为

(6)

(7)

式中：φWT和φPV分别为风电和光伏发电的功率因数。

假设系统负荷功率服从正态分布：

(8)

(9)

式中，σD为负荷功率的标准差，本文取为5%；PD,b和QD,b分别为基态负荷有功、无功功率。

电力市场本身较为复杂，进行准确的市场定价相当困难，因为发电商的报价需要考虑到系统负荷需求、风电功率预测、竞争对手的报价情况等不确定因素。故本文假设发电商报价服从高斯分布：

(10)

式中:μρG为发电商报价均值；σρG为对应的标准差，取为μρG的5%。

2求解算法和流程

2.1UT的基本原理

UT通过非线性变换传递概率分布信息，即根据输入随机变量的概率信息、选定的采样策略，确定性地抽取Sigma样本点，对其进行非线性变换、加权处理，求得输出随机变量的概率分布。

UT的采样策略对采样规模、计算精度至关重要，主要有对称采样策略[15]、最小偏度单形采样策略[18]和超球体单形采样策略[19]等，本文选择求解精度较高且稳定性较好的对称采样策略进行电力市场概率最优潮流的求解。

2.2对称采样策略的UT

对称采样策略的UT需抽取N=2n+1个样本，其中n为输入变量个数。实现步骤可概括为：①采样；②非线性变换；③加权处理并输出。

2.2.1采样

(11)

2.2.2非线性变换

(12)

2.2.3加权处理并输出

对点集{yi}加权处理，得到输出随机变量y的均值uy和协方差矩阵Cyy。

(13)

随着输入随机变量维数n的增加，样本点与中心点ux的距离随之变大，即Sigma样本点较为分散，将造成样本的非局部效应，进而导致高阶项的误差增大。在不确定变量的高阶矩信息处理方面，UT方法并未在算法中直接体现其三阶、四阶矩等高阶参数，而是通过引入比例及高阶信息参数以减小局部效应及高阶项误差。

引入比例修正参数的对称采样的Sigma点为

(14)

(15)

(16)

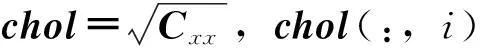
各Sigma点的均值权重及协方差权重为

(17)

(18)

式中:β为高阶项信息参数，用于包含先验分布的高阶矩知识。

2.3UT、MC的相关性处理方法对比

一方面，对于相近区域的风电场、光伏电站和用户，受区域性天气和用户消费习惯的影响；另一方面，发电商的报价又要考虑风电预测、负荷预测等因素；故系统的风速、光照强度、负荷功率和发电商报价之间具有较强的相关性,即体现为具有类似的统计特征。当系统接近运行边界时，相关性会增加系统越限的概率，因而研究随机变量的相关性可更加真实、准确地评估系统的运行情况[20-22]。

研究变量相关性的关键是生成具有特定相关系数且服从指定概率分布的样本，即根据各随机变量的标准差σi以及变量之间的相关性系数φij，经过变换后使得各随机变量具有相关性。各概率求解算法对相关性的处理的不同主要体现在对相关系数矩阵的变换上，下面对UT和MCS的相关性处理方法进行比较。

(19)

2.3.1UT方法

首先，构造协方差矩阵Cxx，然后只需对式(19)的协方差矩阵Cxx进行Choleskey分解，最后按照式(15)、(16)耦合到算法中即可，即UT算法本身集成了处理相关性矩阵的功能，无需其它变换，故其处理随机变量的相关性非常方便高效。

(20)

2.3.2MCS方法

首先，对于式(20)的相关系数矩阵Rxx，MCS生成具有相关性的样本，处理步骤如下：

①对相关系数矩阵Rxx进行choleskey分解以获得三角矩阵L，即Rxx=LLΤ；然后对其进行逆变换以获得正交矩阵B=L-1；

②初始化独立的服从标准正态分布随机样本矩阵us；

侧根与主根相比，其根系粗度较细，而且随着侧根的生长其粗度变化不明显，在程序设计中可以用画线函数进行绘制，为达到平滑侧根生长曲线的目的，采取以若干线段替代直线的方法，每两条线段之间具有一定夹角。

③生成具有式(20)的相关系数且服从正态分布的样本矩阵，即ys=us×B；

④通过式(19)获得具有式(20)相关系数且具有特定均值μ和标准差σ的样本矩阵M。

(21)

式中：diag(σ)为向量σ的对角矩阵。

可以看出，与MCS方法相比，UT方法处理相关性时更为简单、高效，避免了正交变换等复杂过程，在处理相关性方面具有先天优势。

2.4概率最优潮流的计算流程

选择适当的比例缩放参数α和高阶信息参数β。基于UT对式(2)～(10)风、光、荷和发电商报价的概率模型进行抽样，将样本分别代入式(1)的优化模型采用内点法确定性求解，最后UT对结果样本进行加权处理以得到电力市场概率最优潮流模型的运行特征量分布，计算流程如图1所示。

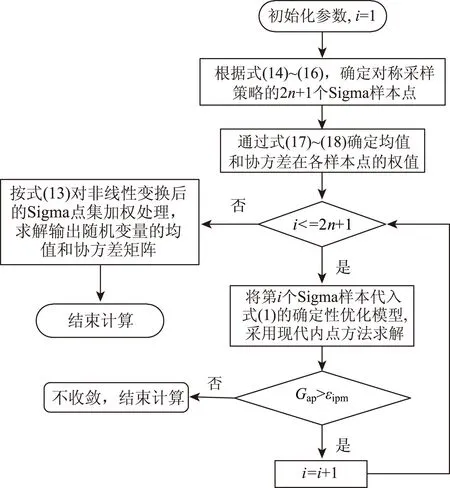
图1　基于UT的概率最优潮流求解流程图

3计算结果及讨论

3.1系统说明

3.2求解性能比较

定义UT与MCS求解结果的相对误差为ε=|(xUT-xMCS)/xMCS|×100%，其中，xUT、xMCS分别为UT和MCS方法的计算输出。计算结果如表1、2所示。

表1　计算时间比较

由表1可以看出：①与MCS方法相比，UT方法的计算效率可提高数十倍，这主要因为UT只需2n+1个样本点；②表2为IEEE30节点系统部分运行特性概率输出及其相对误差比较，可以看出：IEEE30节点系统市场收益的均值相对误差仅为0.119%，标准差相对误差为0.963%；与均值相对误差相比，标准差的总体计算误差相对较大的，即二阶误差大于一阶误差；但总体的相对误差低于3.6%，可见，UT方法的计算结果相当精确。

表2　IEEE30节点系统部分运行特性输出及相对误差ε

图2、3分别给出了IEEE30节点系统无功源QR5的出力的概率密度分布情况和线路25-27的有功功率累积概率计算结果，可以看出：MCS与UT的曲线拟合度较高，且线路25-27的有功功率主要在-8.0～0MW之间分布，求得其在-5.03～-3.43MW之间的概率为0.61，可为运行人员提供线路有功功率在特定区间分布的概率信息。

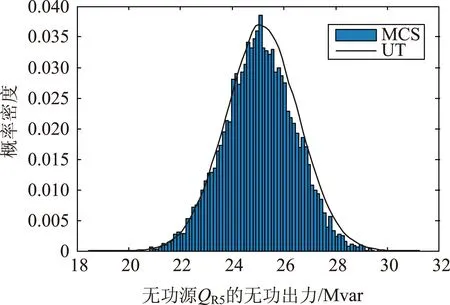
图2　IEEE30节点系统无功源QR5的无功出力

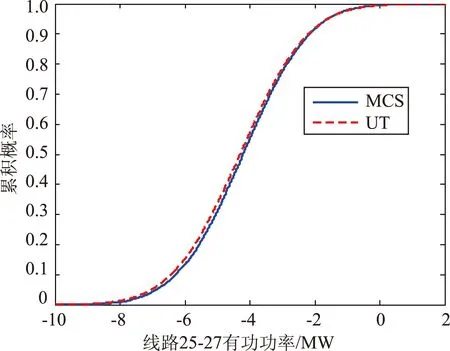
图3　IEEE30节点系统线路25-27的有功功率

表3为MCS和UT计算IEEE118节点系统的部分输出参数及其误差对比，可以看出，UT的均值和标准差输出结果都非常精确，误差均低于2.0%，其中均值误差多数低于1.0%；线路11-13的有功功率均值约为43.4MW，标准差约为4.0，可求出其越限的概率，更便于找到系统线路运行的薄弱环节。

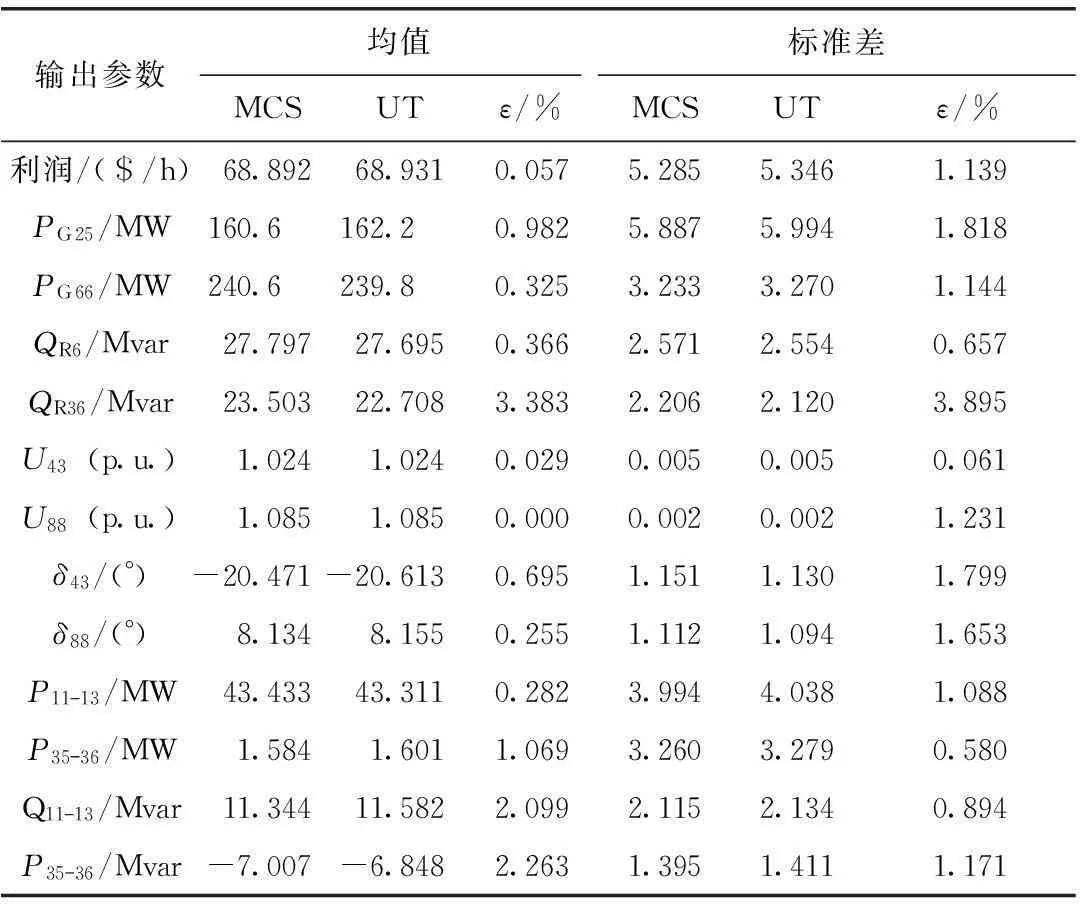
表3　IEEE118节点系统部分运行特性输出及相对误差ε

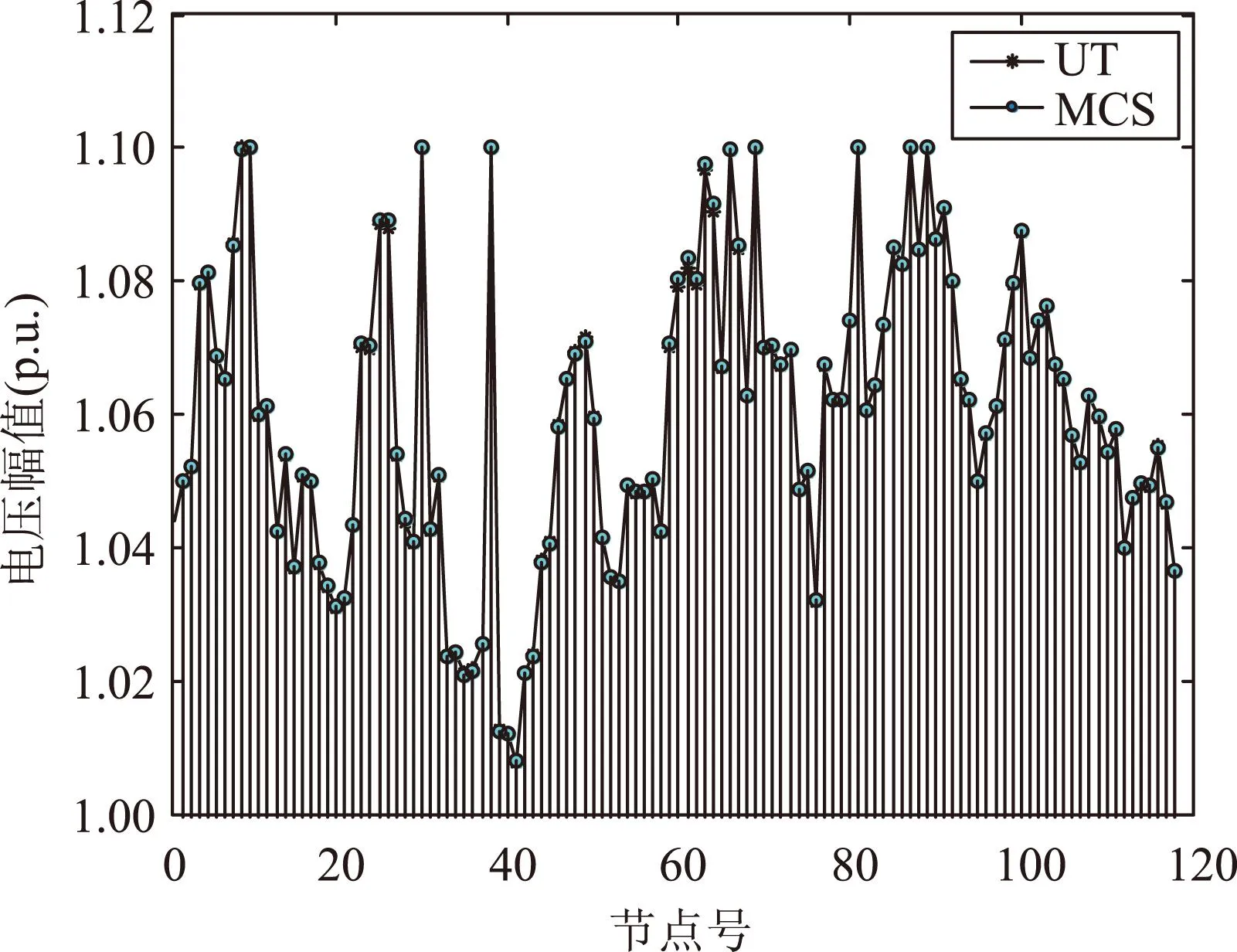
图4　IEEE118节点系统电压幅值

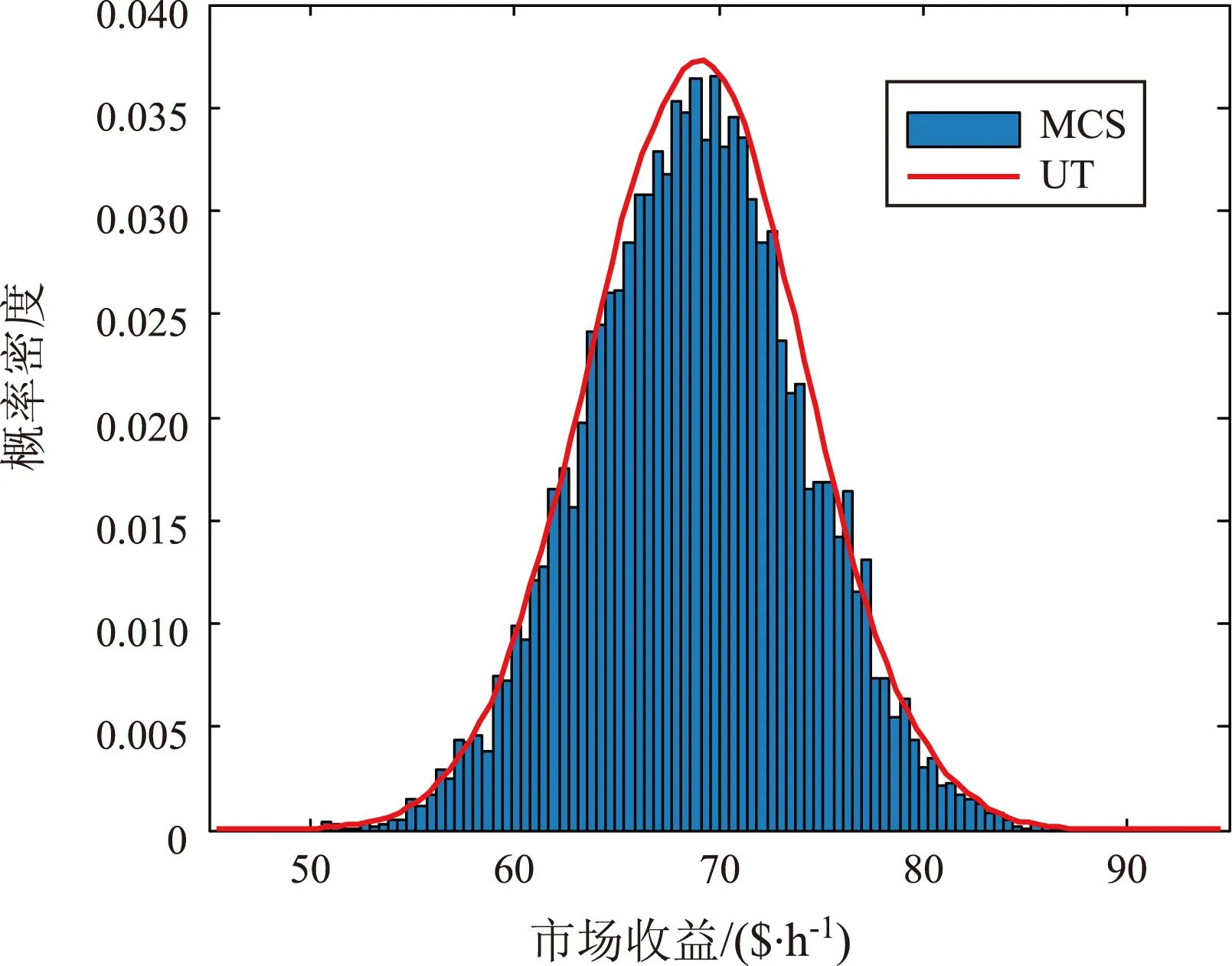
图5　IEEE118节点系统市场收益的概率密度分布

图4为118个节点电压幅值的对比情况，MCS方法的柱状输出与UT方法的电压曲线拟合程度完全满足实际应用的需求。图5为IEEE118节点系统市场收益的概率密度分布情况，市场收益的概率主要分布于52.0～85.0(＄/h)，求得市场收益有0.66的概率分布于63.9～73.9(＄/h)之间，可为市场运行人员准确评估其市场盈利状况提供更为全面的参考。

3.3随机变量相关性分析

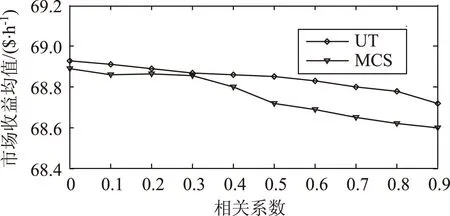
图6　相关性对市场收益均值的影响

图7　相关性对市场收益标准差的影响

由图6、7可以看出，随着相关系数的增加，市场收益的均值在68.6～69.0之间略有变化，但基本保持不变，而其标准差的增加是较为明显的，主要原因是相关性使得各随机变量的波动具有同步性，故增强了电网运行的总体波动性，这也验证了文献[22]指出的相关性对高阶矩的影响相对较大的结论。UT方法对0～0.9范围的相关系数均可处理，且较MCS的计算结果非常接近，但如前文2.3节比较，UT在相关性的处理方面无需正交变换，故优势更加突出。

4结束语

本文针对电力系统中风电、光伏出力，节点负荷功率和发电商报价的不确定性，建立了电力市场环境下的概率最优潮流模型，以准确获取系统运行特征量的统计信息。主要贡献如下：

① 将无迹变换的方法应用于电力市场概率最优潮流的计算，实现方法简单、高效。

② 考虑了风、光、荷以及发电商报价的相关性，并对无迹变换和蒙特卡洛在处理相关性问题上的优缺点进行了比较，验证了无迹变换处理相关性先天优势。

③ 无迹变换输出的系统运行特征量的概率统计信息可为运行人员准确评估系统的市场盈利、系统运行状况，找到运行中的薄弱环节提供更为可靠、全面的参考，以降低市场交易的风险，具有较好的应用前景。

另外，比例缩放参数和高阶项信息参数的取值对UT的求解精度有着重要影响，参数选择策略的研究将是未来改进工作的重点。

参考文献

[1]Gregor Verbic，Claudio A. Caizares.Probabilistic Optimal Power Flow in Electricity Markets Based on a Two-Point Estimate Method[J].IEEE Trans. on Power Systems，2006，21(4)：1883-1893.

[2]王敏，丁明.考虑分布式电源的静态电压稳定概率评估[J].中国电机工程学报，2010，30(25)：17-22.

[3]潘炜，刘文颖，杨以涵.概率最优潮流的点估计算法[J].中国电机工程学报，2008，28(16)：28-33.

[4]黎静华，韦化，莫东.含风电场最优潮流的 Wait-and-See 模型与最优渐近场景分析[J].中国电机工程学报，2012，32(22)：15-23.

[5]王锐，顾伟，孙蓉，等.基于概率最优潮流的风电接入能力分析[J].电网技术，2011，35(12)：214-220.

[6]丁明，李生虎，黄凯.基于蒙特卡罗模拟的概率潮流计算[J].电网技术，2001，25(11)：10-14.

[7]Rodrigues A B，Da Silva M G.Probabilistic assessment of available transfer capacity based on Monte Carlo method with sequential simulation[J].IEEE Trans. on Power Systems，2007，22(1)：484-492.

[8]Morales J M，Perez-Ruiz J.Point estimate schemes to solve the probabilistic power flow[J].IEEE Trans. on Power Systems，2007，22(4)：1594-1601.

[9]杨欢，邹斌.含相关性随机变量的概率潮流三点估计法[J].电力系统自动化，2012，36(15)：51-56.

[10]胡泽春，王锡凡，张显，等.考虑线路故障的随机潮流[J].中国电机工程学报，2005，25(24)：26-33.

[11]Schellenberg A，Rosehart W，Aguado J.Introduction to cumulant based probabilistic optimal power flow[J].IEEE Trans. on Power Systems，2005，20(2)：1184-1186.

[12]石东源，蔡德福，陈金富，等.计及输入变量相关性的半不变量法概率潮流计算[J].中国电机工程学报，2012，32(28)：104-113.

[13]Julier S，Uhlman J.Unscented filtering and nonlinear estimation[J].Proceedings of the IEEE，2004，92(3)：401-422.

[14]Julier S，Uhlman J.A new method for nonlinear transformation of means and covariances in filters and estimators[J].IEEE Trans. on Automation Control，2000，45(3)：477-482.

[15]鲍海波，韦化.基于无迹变换的含大规模风电场电力系统概率最优潮流计算[J].电力系统自动化，2014，38(12)：46-53.

[16]Wei H，Sasaki H，Yokoyama R，et al.A interior point nonlinear programming for optimal power flow problems with a novel data structure [J].IEEE Trans. on Power Systems，1998，13(3)：870-877.

[17]Karaki S H，Chedid R B，Ramadan R.Probabilistic performance assessment of autonomous solar-wind energy conversion systems[J].IEEE Trans. on Energy Conversion，1999，14(3)：766-772.

[18]Julier S，Uhlman J.Reduced sigma point filters for the propagation of means and covariances through nonlinear transformations [C]//Proceedings of the American Control Conference，AK.May 8-10，2002.

[19]Julier S.The spherical simplex unscented transformation [C]//Proceedings of the American Control Conference，USA.June 4-6，2003.

[20]陈雁，文劲宇，程时杰.考虑输入变量相关性的概率潮流计算方法[J].中国电机工程学报，2011，31(22)：80-87.

[21]潘雄，周明，孔晓民，等.风速相关性对最优潮流的影响[J].电力系统自动化，2013，37(6)：37-41.

[22]吴巍，汪可友，李国杰.计及光伏发电相关性的多重积分法概率潮流计算[J].中国电机工程学报，2015，35(3)：568-575.

代景龙(1992-)，男，博士研究生,研究方向为电力系统最优运行与规划，E-mail:jinglong92@163.com；

白晓清(1969-)，女，博士，副教授,研究方向为凸优化理论在电力系统的应用，涉及电动汽车的优化调度、机组组合和经济调度等，E-mail:baixq@gxu.edu.cn。

(责任编辑：杨秋霞)

附录

附表1　IEEE30系统风电场参数

附表2　IEEE118系统风电场参数

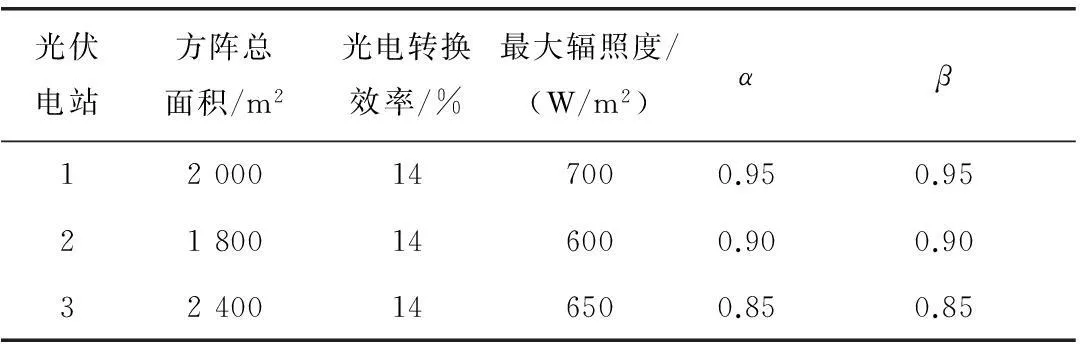
附表3　太阳能光伏发电系统参数

附表4　分布式电源的接入情况

摘要：本文建立了电力市场环境下的概率最优潮流模型，并采用基于对称采样策略的无迹变换方法求解。模型中考虑了新能源出力、负荷和发电商报价的不确定性，揭示了概率性背后隐藏的市场规律和系统运行的薄弱环节；无迹变换方法通过非线性变换传递概率信息，引入比例及高阶信息参数以减小局部效应及高阶项误差，而且对随机变量的相关性影响进行了分析。IEEE30和118节点系统计算结果表明无迹变换方法实现简单高效，可精确求解电力市场的概率最优潮流问题，输出的运行特征量统计信息可为评估系统的市场运行状况提供更为可靠全面的参考。

关键词：电力市场；概率最优潮流；对称采样策略；无迹变换；相关性

Abstract：In this paper, a probabilistic optimal power flow analysis model under electricity market environment is proposed, and is solved by unscented transform method based on symmetric sampling strategy. In order to reveal the market laws and the weaknesses of the operating system by considering probability, the uncertainties of renewable generation output, load demand and bidding are taken into account in the proposed model. In addition, probability information is transferred through nonlinear transformation by using unscented transform, in which the ratio and high-order information parameters are introduced to reduce the local effect and high order errors, and its correlation impact on stochastic variables have been analyzed. Numerical results of IEEE 30-bus and 118-bus test systems show that the implementation of unscented transformation is simple and efficient, can accurately deal with probabilistic optimal power flow problem of electricity market, and the output statistic information of operation characteristics can provide more reliable, comprehensive references for evaluating operation status of electricity market.

Keywords：electricity market; probabilistic optimal power flow; symmetric sampling strategy; unscented transform; correlation

作者简介：

收稿日期：2015-05-24

基金项目：国家重点基础研究发展计划项目(973项目)(2013CB228205)；国家自然科学 (51367004, 51407036)

中图分类号：TM711

文献标志码：A

文章编号：1007-2322(2016)01-0034-07