镀膜机真空室的有限元分析

刘润一，刘东

（北方工业大学，机械与材料工程学院，北京100144）

镀膜机真空室的有限元分析

刘润一，刘东

（北方工业大学，机械与材料工程学院，北京100144）

有限元法是将连续体离散化，通过对有限个单元做分片插值求解各种力学物理学问题的一种数值方法。利用SolidWorks建立镀膜机真空室三维模型，将其通过接口导入ANSYSW orkbench进行有限元分析，通过网格划分，施加载荷，求解计算对模型进行静力学分析得到真空室的变形情况，并在后续优化设计中提供参考。

真空；建模：有限元法；变形

人们在生活中对镀膜产品的需求量越来越大，对于日常生活生产用品的外观的标准也是越来越高，因此，真空镀膜已被广泛应用于各种塑料、陶瓷、玻璃、蜡、木材等制品的表面，金属化真空镀膜技术在今后会有更加光明的发展前途，真空镀膜机的市场肯定会越来越广阔[1]。真空室体是真空镀膜设备中的重要组成部分，镀膜的工作在真空室体中完成，镀膜过程中在外界大气压力的作用下会产生形变，形变的大小，应力的分布会影响镀膜的质量。因此对真空室在大气压力下进行应力应变分析，可以有效地计算分析出真空室在工作室的应力应变分布情况，加以改进，提高镀膜质量。ANSYSWorkbench作为功能强大、应用广泛的有限元分析软件，具有数据统一，良好优化功能及建模、求解和非线性分析功能强大等优点[2]，本文利用ANSYSWorkbench对真空镀膜机真空室体进行应力应变分析，得出了在真空室体的应力应变数值，找出了设计上的缺陷，之后对结构进行了改进。

1理论基础

线性静力分析是最基础但又是应用最广的一类分析类型，线性分析有两方面的含义：首先就是材料为线性，应力应变关系为线性，变形是可恢复的，另外结构发生的是小位移、小应变、小转动，结构刚度不因变形而变化。所谓静力就是结构受到静态载荷的作用，惯性和阻尼可以忽略。在静态载荷作用下，结构处于静力平衡状态，此时必须充分约束，但由于不考虑惯性，则质量对结构没有影响[3]。

经典力学理论可知，物体的动力学通用方程是：

式中，[M]是质量矩阵；[C]是阻尼矩阵；[K]是刚度矩阵；{x}是位移矢量；{F（t）}是力矢量；{x'}是速度矢量；{x''}是加速度矢量。

而现行结构分析中，与时间t相关的量都将被忽略，于是上式简化为：

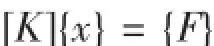
2材料和方法

2.1 三维模型的建立

有限元模型可以直接在ANSYSWorkbench软件中建立，也可以用其他三维软件建立好模型之后导入有限元软件中。本文采用SolidWorks建立好模型，再导入有限元软件中。

镀膜真空室主要由抽气口组件、炉底、炉顶、炉口连接法兰、内筒、外筒、源接口法兰组成，利用SolidWorks三维软件采用拉伸旋转凸台等特征进行建模，附加的功能还包括倒角、切除、阵列等特征方法。为了保证全面准确地反映镀膜机真空的应力应变情况，同时使用有限元模型得到简化，有以下建模原则：

（1）一些明显不会显著影响镀膜机真空室本身整体强度刚度的部位予以简化；

（2）考虑钢板焊接应力及焊缝形式的影响。

本次分析的镀膜机真空室为一空心薄壁圆筒结构，在满足分析要求的前提下，尽量使模型简化，以节省计算时间，所以在建立车架有限元模型时，忽略了一些小零件的作用。在真空镀膜机的真空室模型简化时，三维模型可简化成：主体为Φ495 mm×975 mm的内外圆筒，外接法兰件，把一些无影响的孔洞边角简化掉。如图1所示。

图1 几何模型

2.2 参数及边界条件

边界条件包括约束边界条件和载荷边界条件[4]。真空室主要由各种法兰和圆筒相配合，由焊接而成，在工作中真空室的受力主要来源于真空室和外界大气压的联合作用。不会有在X、Y、Z方向上的移动，真空室的静力分析是计算在固定不变载荷作用下真空室的位移、应力，不考虑惯性和阻尼的影响，所以经过分析为真空室的结构优化设计提供了重要的理论基础以及参考。镀膜机真空室的材料是不锈钢，将不锈钢的材料数据输入到ANSYS中，具体数值如表1所示。

表1 材料参数

2.3 网络划分

网格划分的好坏对于分析结果准确性有重要的影响，ANSYSWorkbench中对于网格划分有扫掠网格划分、四面体网格划分、六面体主导网格划分、以及自动网格划分等方法。根据真空室的工况以及模型的特点，本文采用自由网格划分以及局部细化的组合划分方式，划分后如图2所示。本模型共有159601个节点，77045个单元。

图2 网格划分

2.4 施加载荷并求解

可以在前处理器中对几何模型上市价力载荷和约束。力载荷包括点载荷、分布载荷、体载荷、函数载荷等。施加载荷也可在分析计算中进行，其效果完全一样[5]。如图3、图4所示。

图3 施加约束

图4 施加载荷

（1）对真空室底面施加约束ALLDOF；

（2）对真空室外表面施加1标准大气压，施加室。

2.5 分析结果

后处理是ANSYSWorkbench软件分析最重要的步骤，后处理可以看到真空室在实际工作中的情况和数据，在对结果进行深入的分析之后才能发现三维模型的缺点、优点，之后可以提出进一步的解决办法，提高镀膜机的工作效率以及镀膜质量。这样就可以提前对结构进行更改，节省了现实中的浪费，通过等效应力云图可以直观看出各部位应力的强弱，通过变形云图可以得到各部分之间的变形情况。

镀膜机真空室的静力分析是计算在固定不变载荷作用下的位移、应力，它不考虑惯性和阻尼的影响。真空室为有限元分析的主体，在后处理过程中只显示真空室的变形和应力云图，这样能够简化分析结果，突出重点。真空室的变形如图5所示，应力云图如图6所示，应变云图如图7所示。

图5 真空室的变形图

如图5所示，真空室最小位移处在真空室桶臂顶端，最大位移变形处位于真空室与法兰连接薄板处，最大位移为1.928 mm，真空室的顶端位移变形情况也比较明显，顶端的中心向下凹陷。如图6所示，真空室的最大应力在真空室的筒壁上以及真空室与法兰连接处，大小为291 MPa.为了进一步优化，在筒壁四周加了五根筋板，真空室的变形图、应力云图、应变云图如图8、图9、图10所示。

图8 真空室的变形图

图6 真空室的应力云图

图7 真空室的应变云图

图9 真空室的应力云图

图10 真空室的应变云图

综合以上分析结果，将数据归纳于表2、表3所示。

表2 真空室的有限元分析结果

表3 优化后真空室的有限元分析结果

通过表2和表3的对比可以看出在优化前真空室体模型变化的最大变形量位于法兰与桶壁的连接处，最大变形量为为1.928 1 mm，等效应力为291 MPa，等效应变为0.001 8位于法兰与桶壁的连接处，通过在桶壁两侧加上筋板之后总变形量减小到0.758 5 mm、等效应力减小到185 MPa、等效应变为0.000 1，变形明显减小，进一步提高了镀膜质量。

3结束语

通过应用ANSYSWorkbench软件对镀膜机真空室进行有限元分析，得到了单元和节点的应力应变云图和位移图，可以得到以下结论：镀膜机真空室的顶盖部分以及筒壁有明显的变化情况，有明显的向内凹的趋势，是真空室的应变最大处，而且顶盖中心受向下的压力，向内部凹陷。在优化前真空室体的最大变形量为1.928 1 mm，最大等效应力为291 MPa，最大等效应变为0.001 8m/m，虽然形变量在可接受的范围内，但是为了提高镀膜产品的质量，需要进一步优化进一步减小变形量。针对真空室箱体存在较大变形的位置，在真空室筒壁四周加上筋板，使变形量减小到0.758 5 mm，最大等效应力减小到185 MPa使真空室的形变对真空镀膜过程影响最小，提高了镀膜质量。

[1]邸英浩，胡晓锋，李红娟.浅析真空镀膜技术的现状及进展[J].天津冶金.2004（05）：45-48.

[2]梁俊涛，张莉，梁涛.基于ANSYSWorkbench的工装结构设计与优化[J].设计与研究，2014（2）：21-22.

[3]LI Bing.He Zhengjia.Chen Xuefeng.ANSYS Workbench design.simulation and optimination[M].Beijing Tsinghua Uni versity Press.2012：149-153.

[4]Cong Ming.Zhao Qiang.Han Tao.Influence of different boundry constraint in static and dynamic analysis[C].2010 International Conference on Mechanic Automation and Contral Engineering.June 26.2010-June 28.2010.Wu han.China：IEEE Computer Society.

[5]许进峰.ANSYSWorkbench 15.0完全自学一本通[M].北京：电子工业出版社，2014：199-203.

The Finite Element Analysis of the Vacuum Chamber of the Coating Machine

LIU Run-yi，LIU dong
（School Of Mechanical And Material Engineer，North China University of Technology，Beijing 100144，China）

The finite elementmethod make the continuousmedium discrete，and the slice interpolation method is applied to finite element to solve all kinds ofmechanical problems and physics problems.Then using Solidworks to model the vacuum chamber and simplify the model.Then using the ANSYSWorkbench to mesh the model and apply load to the model then ststic analysis of the model.At last the deformation condition of the model is optimized.

vacuum；modeling；finite elementmethod；deformation condition

TB753.2

A

1672-545X（2016）12-0024-04

2016-09-22

刘润一（1989-），男，北京人，硕士研究生，研究方向：数控加工技术与装备；刘东（1976-），男，山西人，副教授，博士研究生，研究方向：先进制造技术。