“高分四号”卫星面阵凝视相机超分辨技术

刘薇 高慧婷 曹世翔 何红艳 谭伟

（北京空间机电研究所，北京 100094）

“高分四号”卫星面阵凝视相机超分辨技术

刘薇 高慧婷 曹世翔 何红艳 谭伟

（北京空间机电研究所，北京 100094）

“高分四号”（GF-4）卫星是中国首颗高分辨率地球静止轨道卫星，在防灾减灾、环境监测、天气预报等领域具有重大的应用价值。GF-4卫星相机采用面阵探测器，具有凝视观测、时间分辨率高等特点。根据GF-4卫星的成像特点，对GF-4卫星影像进行超分辨重建，可得到分辨率更高的卫星影像。文章针对遥感影像超分辨率重建需要解决的三个问题：图像配准、点扩散函数（Point Spread Function，PSF）的准确测量和超分辨率重建算法进行了研究。使用了精确测量PSF的改进凸集投影超分辨重建方法对 GF-4卫星在轨图像进行了验证。测试结果表明，经超分辨重建后的影像在保持清晰度和信息细节的同时，分辨率得到了较大提高。该方法在面阵凝视空间相机遥感图像的超分辨重建领域具有良好的应用前景。

精确测量点扩散函数 改进凸集投影法 超分辨率 面阵相机 “高分四号”卫星

0 引言

“高分四号”（GF-4）卫星是我国第一颗高分辨率地球静止轨道遥感卫星，携带超大面阵凝视相机，具有观测位置相对固定、时间分辨率高等特点。GF-4卫星相机的成像模式和特点，使其具备了进行序列图像超分辨重建的基础[1]。

超分辨率技术（Super Resolution，SR）[2]是从获取的低分辨率（Low Resolution，LR）影像重建出高分辨率(High Resolution，HR)的影像[3]。超分辨率重建技术的研究与应用，可以充分发掘现有遥感影像数据的潜力[4]，在尽量减少硬件改变的前提下，得到高于系统设计分辨率的遥感影像，更好服务于防灾减灾、环境监测、天气预报等领域。

目前在遥感领域的超分辨率重建应用比较少，较为成功是 SPOT5卫星[5]和 OrbView-3的超模式（Supermode）。其设计是使用两个同样的CCD线阵，在沿轨和垂轨方向各错开0.5个像元来提高影像的采样密度，从而达到提高分辨率的效果。这种超模式是通过硬件直接克服图像配准的问题。理论上空间分辨率可以是原来的2倍，真正的图像品质会略差于理论值，SPOT5获得的超分辨重建图像分辨率大约为原有分辨率的1.7-1.85倍。

另一遥感应用案例是日本ALOS卫星PRISM三线阵传感器，可以同时生成同一地区的三张影像[6]，利用这3张低分辨率影像来生成高分辨的影像。ALOS卫星PRISM三线阵传感器遥感影像进行超分辨重建的分辨率提高倍数目前没有评估。

SPOT5、OrbView-3和ALOS卫星都采用推扫成像，在硬件上采用多个传感器同时成像的方法得到同一地物的序列图像。与这些卫星不同，GF-4卫星上装载面阵凝视相机，可在很短时间内对同一场景进行重复采样得到序列图像，为超分辨重建提供了实现前提。

GF-4卫星遥感影像超分辨率重建需要解决三个问题：1）图像配准[7-9]；2）点扩散函数（Point Spread Function，PSF）的准确测量；3）超分辨率重建算法。

1 图像配准

（1）图像分块

选取子块，对每一个子块SubA与SubB，完成特征点选取、特征向量生成、同名点匹配操作：

1）特征点选取[10]：构建SubA与SubB的尺度空间，需完成6次高斯滤波，从滤波结果中选取局部的极值点作为特征点。

高斯滤波记为：

式中 x,y表示图像子块的位置，σ表示尺度。

从中间3层DOG每个像元出发，比较其上下和周边26像元，确定当前像元是否为极值，作为特征点P。图1为多组尺度空间特征点提取示意。

2）特征向量生成：计算特征点P周围的梯度直方图，将区域划分为4×4个子区域，其中，每个区域有八个梯度向量，按照高斯窗加权累计到P点，得到主方向Φ，并将坐标按照主方向进行旋转，以达到旋转不变性，最后得到4×4×8=128维向量D：，并对它进行整体归一化，从而最终得到特征点的描述向量。

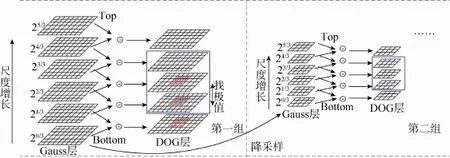
图1 构造SIFT分层Fig.1 The octave and layer construction of SIFT

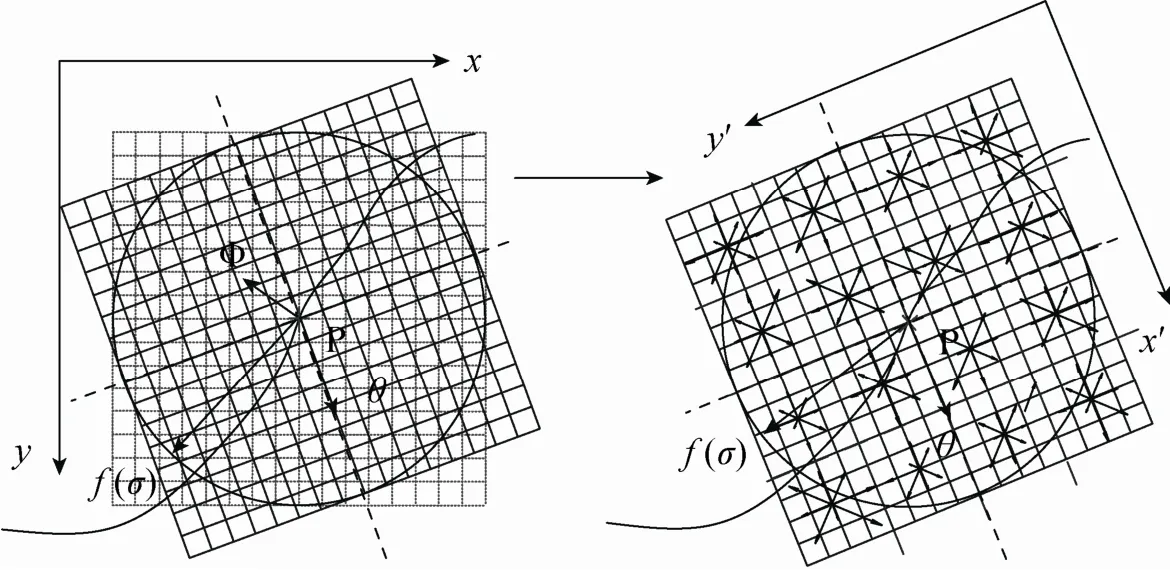
图2 生成特征向量Fig.2 Feature description using principle direction

3）同名点匹配：按次近、最邻近比值完成两幅子块间的特征向量对应，同时得到特征点匹配结果，即寻找图像A中某一特征向量在B中的最小距离d0和次最小距离d1，当时，认为最小距离对应的向量点为匹配点。

（2）计算图像关系

根据所有的特征点像元对应关系，计算两个图像的多项式变换结果。P2( x, y)、P2( x, y)分别为两个图像的特征点集。按最小二乘求解两个图像特征点集的二次方程式多项式系数 (a0, a1, a2, a3, a4, a5)和(b0, b1, b2, b3, b4, b5)，然后即可计算两幅图像的相对关系：

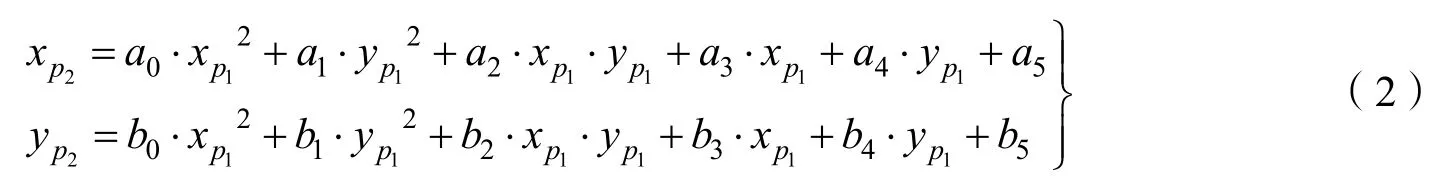
式中 (xp1,yp1)和 (xp2,yp2)两幅图像中对应的点，作为超分前的配准结果。

2 PSF测量

PSF是光学系统的模糊核，也是各种复原和超分辨重建方法的基础[11]，准确测量光学系统和探测器的PSF能为超分辨重建奠定坚实基础，大幅提高重建品质[12]。

根据GF-4卫星相机特点，本文进行了基于相位PSF靶标的GF-4卫星全色面阵相机分视场PSF测量，通过相位靶标设计来保证PSF准确性，通过多次测量来降低图像噪声和统计涨落的影响。精确测量PSF能为超分辨重建提供准确物理约束，提高重建图像的正确性。

2.1 靶标设计

受实验室测试平台振动等实验条件影响，为了保证实验室测试数据有效性，设计错相位星点靶标阵列控制相位靶标，保证每帧图像至少有一个星点在一个像元内成像，从而保证PSF测量的准确性。此外，通过多次采样测量，降低图像噪声和统计涨落的影响。

图3 相位PSF靶标Fig.3 Phase PSF Target

2.2 PSF计算

1）对相位 PSF靶标成像 100帧以上，对每一帧图像的点源进行相位筛选。点源为pi, j(i =0,1,… ,9; j =0,1,… ,9)，设p0,0相位为 (θx0,0,θy0,0)，则点源pi, j的相位为：

式中 mod表示取余数。根据式（3），得到100组子块灰度分布矩阵 DNx, y（即点源相位模板），其中x=0,1,… ,9； y=0,1,… ,9。

为了确定待测点源的准确相位，提取待测点源子窗口图像 DNm, n，图像大小与相位模板相同，设计目标函数J( x, y)如下：

式中 J( x, y)表示两组向量比值均方根，J( x, y)最小值时，表示 DNx, y与 DNm, n最接近时，对应 DNx, y对应的相位即为待测点源的准确相位：

2）对每一帧靶标图像的满足相位为(0,0)的星点利用高斯函数 N(μ1, μ2,σ1,σ2)进行拟合，得到每一帧图像高斯分布点扩散函数方差和。

3）计算每一帧图像的高斯分布点扩散函数方差，最终得到高斯分布点扩散函数方差序列σp1和σp2，对σp1和σp2作直方图分布统计，得到直方图序列，并将该直方图序列拟合得到高斯分布函数N(μh1,μh2,σh1,σh 2)， N (0,0,σh1,σh2)即为GF-4卫星相机的点扩散函数。

2.3 分视场PSF测量

在传统凸集投影（Project onto Convex Sets，POCS）算法中，通常选用盲的高斯模糊核函数，而单一的模糊核函数无法真实描述全图像的模糊情况，为了保证测量的PSF能进行准确的超分辨重建，本文采用了分视场PSF测量，一共进行了GF-4卫星相机9个视场的PSF测量。

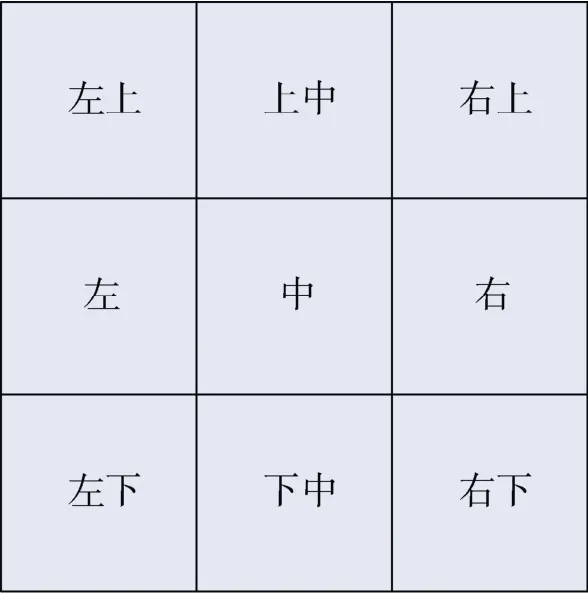
图4 测量视场示意图Fig.4 Measurement field of vision

3 改进POCS超分辨重建方法

POCS方法是一种空域超分辨重建方法[13]，这种方法和最大后验概率法（MAP）[14-15]等超分辨重建方法相比，原理直观，算法简单，是目前序列图像超分辨重建的研究热点之一。把成像系统先验知识作为进行图像重建的约束条件[16]，每个约束条件对应于在整个成像空间中的一个含有理想高分辨率影像的凸形约束集。这组凸形约束集代表了期望的高分辨率影像的一些特性，如正定、能量有界等，通过这些约束集就可以得到简化的解空间。

低分辨率图像的超分辨重建可表达为：

式中 yi表示大小r1×r2的LR图像；z表示的HR图像（N表示分辨率提高倍数）；H为点扩散函数；nk为噪声。

3.1 边缘幅度约束因子

传统POCS算法中残差阈值通常选定一个常数，点扩散函数假设为单一的高斯模糊函数，对全局的迭代投影采用相同程度的一致性约束，造成某些位置（例如边缘）出现欠投影或过投影，形成边缘振荡效应。本文算法将基于分视场的精确PSF测量结果，设为点目标的初始高分辨率图像，构造边缘幅度约束因子为：

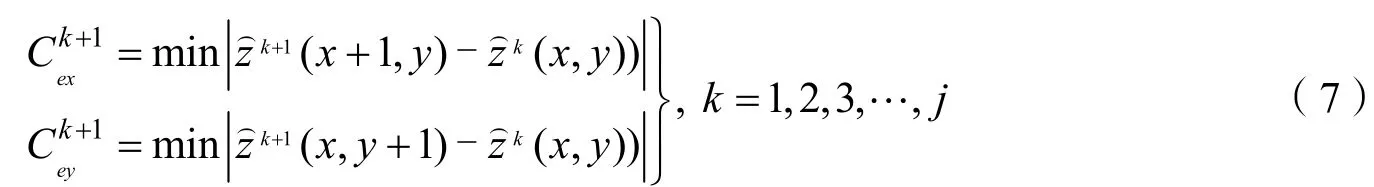
3.2 投影操作

由于精确测量了GF-4不同视场的点扩散函数，本文采用精确测量的分视场PSF进行投影修正。

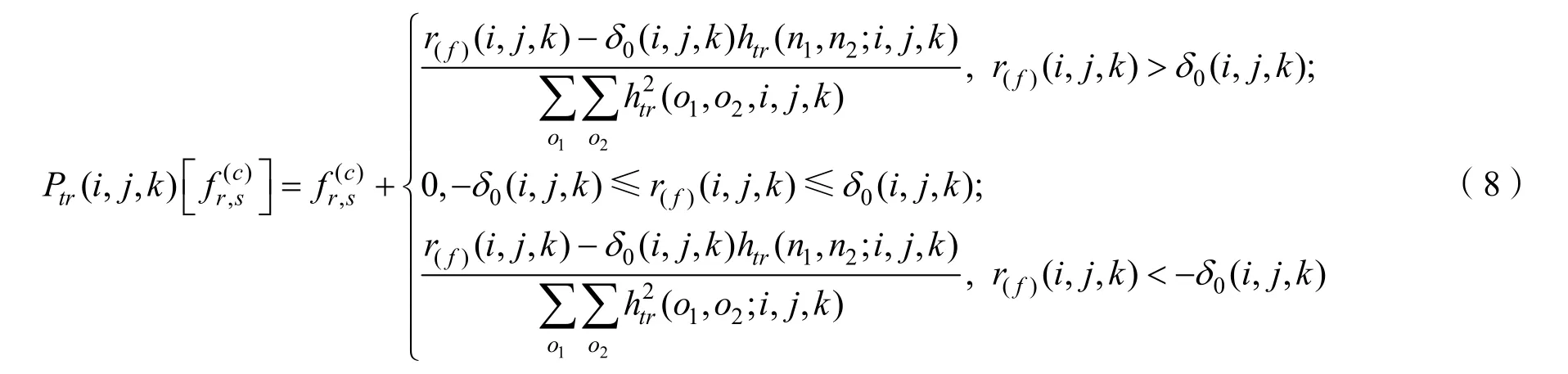
式中 htr(n1, n2; i, j, k)表示图像的模糊核PSF。

在上述投影操作下，HR图像的估计值 ˆ(c) f 可以从所有低分辨图像中迭代求解得到，可以采用投影算子Ptr和PA。理论上要求迭代到最终的高分辨率图像估计值位于所有限制集的交集中。

3.3 分视场图像边缘修正

由于 GF-4卫星图像经过不同视场点扩散函数投影操作后，在视场边缘有可能出现不均匀的边缘现象。由于视场边缘是由不同视场的PSF共同影响下得到的图像，所以本文采用分视场边缘图像权重修正法进行。分视场边缘的图像修正根据下式进行：

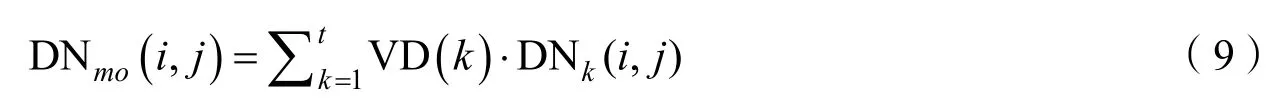
式中 DNmo（i, j）为修正后的图像灰度值； VD（ k）为边缘像元到第k个分视场的空间距离；DNk(i, j)为第k个分视场(i, j)位置上的图像数值。

3.4 超分辨重建详细算法

Step1：确定参考帧图像，采用双线性或三次样条内插得到初始高分图像。

Step2：设置迭代次数。

Step3：对每一帧低分辨图像进行迭代计算：

Step3.1：进行图像精配准，得到每一帧低分图像相对参考帧的运动向量；

Step3.2：计算每一个迭代步数的投影约束集；

Step3.3：根据精确测量的PSF对每帧低分辨率图像进行投影迭代；

Step3.4：计算每一步的迭代残差；

Step3.5：根据残差修正高分辨率图像。

Step4：检查是否达到迭代次数，并进行分视场图像边缘修正，得到超分辨重建图像。

4 GF-4在轨图像验证

4.1图像处理结果

根据文中提出的基于精确测量PSF的改进POCS超分辨重建方法，选用三组（每组6帧）GF-4卫星在轨图像作为试验对象进行测试，是很短时间内对同一场景成像的多幅图像。同时，使用基于盲估计PSF的POCS超分辨重建方法和最大后验概率法的超分辨率重建方法对这三组图像进行了处理，图像处理结果如下：

图5 低分变率图像和不同超分辨率重建方法处理图像Fig.5 LR Picture & HR picture of different method

从图5可见，由于GF-4卫星图像幅宽大，使用基于盲估计PSF的POCS超分辨重建方法处理的图像在图像的一部分区域处理效果好，但另一部分处理效果不好，说明盲估计的PSF不能适用于GF-4图像的全局处理；使用 MAP超分辨率重建方法处理的图像部分区域出现锯齿噪声；而本文方法在提高分辨率的同时很好的保持了图像细节，分块处理的方法避免了PSF的区域效应，边缘幅度约束因子也保证了不会出现边缘振荡效应。

4.2 相关指标计算

对以上三组实验进行超分辨处理的品质量化指标评价，采用指标包括分辨率提高、图像清晰度（图像中景物边缘的锐利程度，用边缘灰度变化程度表征，代表图像对景物细节的还原能力和微小细节的感知能力，数值越大越好）、信息熵（代表图像信息量，数值越小代表图像信息量越大）、峰值信噪比（PSNR数值越大，代表图像失真越少）、均方误差（MSE，图像平均误差，数值越小越好）。

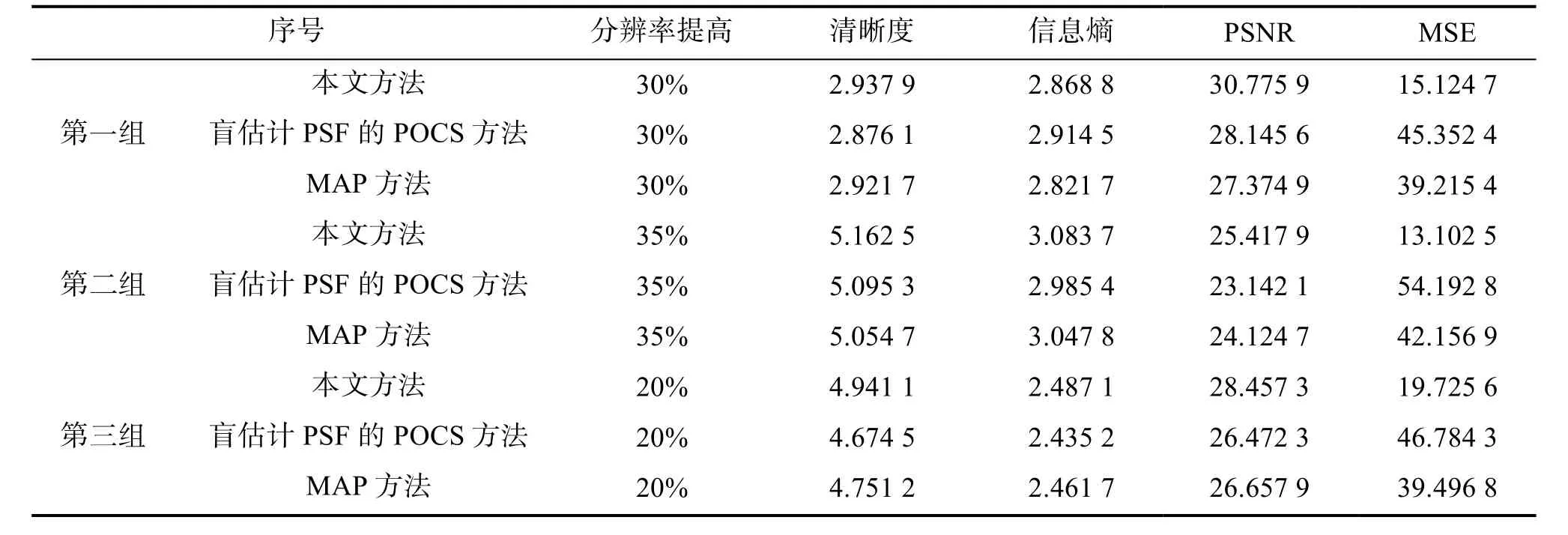
表1 不同方法指标Tab. 1 Different method index

从表1可以看出，本文方法在图像分辨率提升一样的前提下，清晰度[17-18]、信息熵等指标好于其他两种方法，说明恢复的图像高频信息多于其他两种方法；峰值信噪比、均方误差指标好于其他两种方法，说明在提升分辨率，恢复高频信息的同时，在噪声抑制方面也表现更好。

5 结束语

本文提出的改进POCS方法是建立在对GF-4成像系统（相机）测试精确PSF基础上的，与其他方法相比，能得到接近真实的约束集。而且，本文提出的方法能有效的抑制边缘振荡效应，在提高图像分辨率的同时，清晰度和信息量等方面也得到了明显提升。

本文提出的方法已经经过了在轨图像的验证，可以为面阵凝视型相机的超分辨重建工程应用提供借鉴。

References)

[1] STARK H, OSKOUI P. High Resolution Image Recovery from Image-plane Arrays, Using Convex Projections[J]. Journal of the Optical Society of America Optics & Image Science, 1989, 6(11): 1715-1726.

[2] BAKER S, KANADE T. Limits on Super-resolution and How to Break Them[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2000, 2(9): 1167-1183.

[3] FASIU S, ROBINSON D, ELAD M, et al. Advances and Challenges in Super-resolution[J]. International Journal of Imaging System & Technology, 2004, 14(2): 47-57.

[4] GETREUER P. Image Interpolation with Geometric Contour Stencils[J]. Image Processing On Line, 2011, 4(3): 954-979. DOI: 10.5201/ipol.2011.g_igcs

[5] TAN Bing, XING Shuai, XU Qing, et al. A Research on SPOT5 Supermode Image Processing[J]. Remote Sensing Technology & Application, 2004, 19(4): 249-252.

[6] 范冲, 龚健雅, 朱建军, 等. ALOS-PRISM遥感影像超分辨率重建[J]. 遥感学报, 2009, 13(1): 75-82.

FAN Chong, GONG Jianya, ZHU Jianjun, et al. Super-resolution Reconstruction of ALOS-PRISM Remote Sensing Images[J]. Journal of Remote Sensing, 2009, 13(1): 75-82. (in Chinese)

[7] DONG Weisheng, ZHANG Lei, SHI Guangming, et al. Image Deblurring and Super-resolution by Adaptive Sparse Domain Selection and Adaptive Regularization[J]. IEEE Trans. Image Processing, 2011, 20(7): 1838-1857.

[8] FONSECAL M G, COSTAM H M. Automatic Registration of Satellite Images: IEEE Brazilian Symposium on Computer Graphics and Image Processing[C]. Campos do Jordao: IEEE, 1997: 219-226. DOI:10.1109/SIGRA.1997.625182.

[9] HSIEH J W, LIAOH Y M, FAN K C, et al. Image Registration Using a New Edged-approach[J]. Computer Vision and Image Understanding, 1997, 67(2): 112-130.

[10] DONG Weisheng, SHI Guangming, ZHANG Lei, et al. Super-resolution with Nonlocal Regularization Sparse Representation: Visual Communication and Image Processing 2010[C]. Huangshan: SPIE, 2012. DOI: 10.1117/12.863368.

[11] LIU Changmen, CHEN Xi. Point Spread Function (PSF) Measurement for Cell Phone Camera with a High Resolution PSF of the Imaging Lens and a Sub-pixel Digital Algorithm[C]//SPIE Proceedings Vol. 7072: Optics and Photonics for Information Processing II. SPIE, 2008. DOI: 10.1117/12.796034.

[12] TAKACS P Z, KOTOV I, FRANK J, et al. PSF and MTF Measurement Method for Thick CCD Sensor Characterization[J]. Proc. SPIE, 2010, 7742(9): 774207-774207-12.

[13] FAN Chong, GONG Jianya, ZHU Jianjun. POCS Super-resolution Sequence Image Reconstruction Based on Image Registration[J]. Acta Geodaetica Et Cartographica Sinica, 2006, 35(4): 358-363.

[14] YANG Xin, WANG Chongqing, FEI Shumin. An Adaptive Technology for SAR Image Blind Super-resolution Based MAP[J]. Journal of Astronautics, 2010, 31(1): 217-221.

[15] HARDIE R C, BARNARD K J, AMSTRONG E E. Joint MAP Registration and High-resolution Image Estimation Using a Sequence of Undersampled Images[J]. IEEE Trans image Processing, 1997, 6(10): 1621-1633.

[16] LU Yao, INAMURA M. Spatial Resolution Improvement of Remote Sensing Images by Fusion of Subpixel-shifted Multi-observation Images[J]. International Journal of Remote Sensing, 2003, 24(23): 4647-4660.

[17] 刘薇, 高慧婷, 王治强, 等. “实践九号”A卫星图像的直接解调成像方法[J]. 航天返回与遥感, 2013, 34(5): 63-69.

LIU Wei, GAO Huiting. WANG Zhiqiang, et al. Direct Demodulation Method Applied in Remote Sensing Images of SJ-9A Satellite[J]. Spacecraft Recovery & Remote Sensing, 2013, 34(5): 63-69.(in Chinese)

[18] 谭伟, 杨秉新, 何红艳. 一种新的遥感影像清晰度评价方法[J]. 中国空间科学技术, 2016, 36(2): 50-57.

TAN Wei, YANG Bingxin, HE Hongyan. A New Definition Evaluation Method for Remote Sensing Image of Satellite[J]. Chinese Space Science and Technology, 2016, 36(2): 50-57.(in Chinese)

Study on Super Resolution of GF-4 Satellite Staring Plane Array Camera

LIU Wei GAO Huiting CAO Shixiang HE Hongyan TAN Wei

（Beijing Institute of Space Mechanics & Electricity, Beijing 100094, China）

GF-4 Satellite is the first Chinese high resolution geostationary orbit satellite, and it has important application value in disaster prevention and reduction, environmental monitoring, weather forecast and so on. The camera of GF-4 satellite adopts array detector, which has the characteristics of staring observation and high time resolution. According to the imaging characteristics of GF-4 satellite, we can get a higher resolution satellite image with a super resolution reconstruction of the GF-4 satellite image. The article studies three following problems need to be solved for the remote sensing image super resolution reconstruction: image registration, the accurate measurement of point spread function and algorithm of super resolution reconstruction. An improved project onto convex sets super resolution reconstruction method based on accurate measurement is used to verify the images of GF-4 satellite. The verification results show that after super resolution reconstruction, the resolution of images are greatly improved while maintaining clarity and details of the information. This method has a good application prospect in the field of super resolution reconstruction of the image of plane array staring space camera.

accurate measurement of camera point spread function; improved project onto convex sets method; super resolution; plane array camera; GF-4 satellite

V443.5

: A

: 1009-8518(2016)04-0087-09

10.3969/j.issn.1009-8518.2016.04.012

刘薇，女，1977年生，2006年获中国科学院空间物理专业博士学位，高级工程师。研究方向为遥感图像处理与应用。E-mail：liuweibee@126.com。

（编辑：毛建杰）

2016-06-08

高分辨率对地观测系统重大专项（50-Y20A08-0508-15/16）