中厚煤层综采工作面支架实时工作阻力确定
陈磊
(中国矿业大学(北京) 资源与安全工程学院, 北京 100083)
中厚煤层综采工作面支架实时工作阻力确定
陈磊
(中国矿业大学(北京) 资源与安全工程学院, 北京 100083)
为研究中厚煤层综采工作面液压支架实时工作阻力随顶板断裂的演化过程,建立了基于弹性基础梁的采场顶板力学模型,分析了顶板运移规律,指出上覆岩层超前工作面断裂,给出了超前断裂距的解析解。结合工程实际,分析了工作面初次来压和周期来压时顶板破断形式,得到了周期来压期间支架实时工作阻力的计算公式。研究结果表明:单个来压周期内老顶发生2次断裂,初次破断前,支架工作阻力是关于老顶悬露长度的非线性函数,当悬露长度达到极限破断距时,老顶发生破断,支架工作阻力达到最大值;二次破断前,支架工作阻力随工作面推进呈二次函数式增大,老顶发生破断时达到最大值。
煤炭开采; 围岩控制; 液压支架; 支架工作阻力; 弹性基础梁; 超前破断距; 来压步距
0 引言
近年来,随着煤炭开采技术的不断发展,综合机械化采煤技术日趋成熟,逐渐实现了矿井安全高效生产。随着采场围岩控制理论研究的不断完善[1-2],工作面液压支架工作阻力的确定逐渐科学化,但还无法达到准确求解的程度[3]。王家臣等[4]通过研究薄基岩破断特征,提出利用顶板动载荷估算液压支架工作阻力的新方法;杨胜利等[5]采用试验、数值模拟等方法研究了大采高覆岩变形特征,分析了不同顶板结构形态下支架工作阻力的确定方法;煤炭科学研究总院对现场观测数据进行统计分析,建立了一种确定支架工作阻力的统计方法,并给出了支架支护强度的计算公式[6];还有一些学者针对不同的开采条件,研究了厚煤层综放开采时支架工作阻力的确定方法[7-8]。在工程实际应用中,最简单且最常用的方法是选取工作面采高的4~8倍岩柱质量作为支架的额定工作阻力。以上方法都可以确定支架的额定工作阻力。采煤工作面推进过程中,液压支架的实时工作阻力依靠现场观测数据计算得出[9]。本文选取某煤矿某综采工作面,在分析老顶及上覆岩层岩性的基础上,研究采场覆岩运移规律,通过分析采场矿压显现规律,找到确定工作面液压支架实时工作阻力的理论计算方法。
1 顶板运移基本规律
采煤工作面沿开切眼向前推进,顶板悬露在采空区,当悬露长度达到其极限跨距时,老顶发生破断。老顶初次破断前,形成两端固支、两侧半无限长的弹性基础梁结构,如图1(a)所示,其中F为固支端反力,M为固支端弯矩,q为载荷。两端的支座为破碎垮落的直接顶,视为垫层。设垫层系数(使地基产生单位沉陷所需的压强)为k0,沉陷量为ω,则单位面积的垫层对顶板的支撑力为k0ω[10]。
老顶初次破断前,顶板的受力可简化成如图1(b)所示的弹性基础梁与悬臂梁的组合结构。取采空区右侧边界为坐标原点o建立直角坐标系,采空区中部的横坐标为-l,可将老顶视为带有向下均布载荷q的悬臂梁。可得单位宽度梁的挠曲方程为[11]
式中:E为老顶的弹性模量;I为老顶截面惯性矩;ω为老顶挠度。
将边界和连续条件代入式(1)和式(2),即可求出老顶挠度,进而可求解出弯矩和剪力。
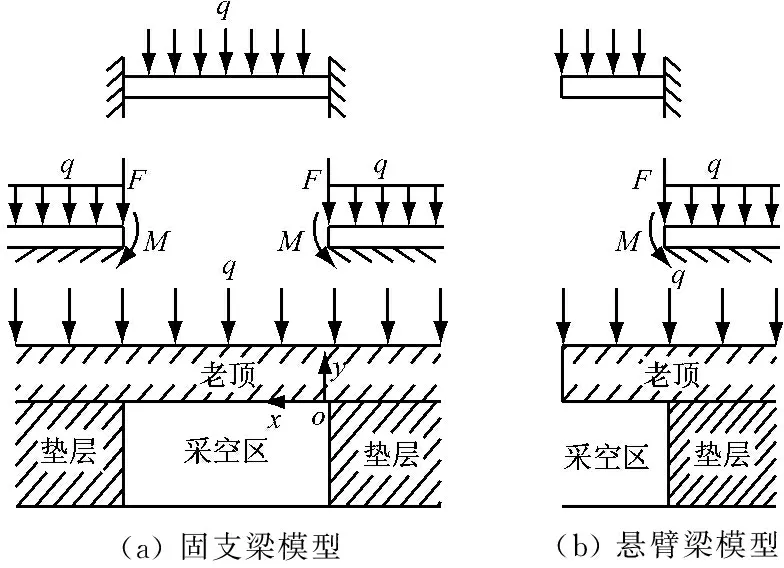
图1 弹性基础梁力学模型
当老顶发生周期破断时, 老顶在x≥0处的挠曲方程为[11-12]
(3)

将顶板视为悬臂梁,则破坏位置发生在弯矩最大值处,而整个梁结构弯矩最大值在x≥0处。当y(3)=0时,弯矩取得最大值,其位置记为xβ,则有
(4)
由式(4)可知,xβ恒大于0,即老顶弯矩最大处在采空区边界之前,则老顶发生周期破断时,破断位置总是超前工作面。超前破断距与悬臂梁悬露长度及梁的特征系数有关。
2 采场覆岩破断形式
以某煤矿15201综采工作面为工程背景,研究采场顶板的破断形式和工作面来压情况。15201综采工作面煤层厚度为2.37~2.76 m,平均厚度为2.53 m,煤层倾角平均为6°;采用倾斜长壁一次采全高采煤方法,工作面长度为200 m。其采场顶板物理和力学性质见表1。直接顶为泥岩,随采随落,起支撑顶板作用。参照文献[13],设置垫层系数k0=0.3 GN/m3。支架中心距a=1.5 m,控顶距c=6 m。
2.1 工作面初次来压
采场覆岩由多层岩石组成,每一层同时受上覆岩层和下部岩层的作用,上覆岩层的作用简化为载荷,下部岩层的支撑作用等效为弹性地基。建立如图2所示的采场覆岩破断模型,直接顶随采随冒,老顶的悬露长度不断连续变长,在老顶破断之前,对上部岩层始终起支撑作用。当老顶悬露长度达到其极限跨距时,老顶首次破断,支架工作阻力增大.但单层岩层破断带来的压力不一定能达到来压的程度,因此定义除老顶外多层顶板破断时工作面才会来压。

表1 采场顶板物理和力学性质
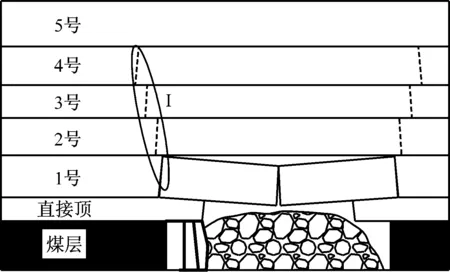
图2 采场覆岩破断模型
如图2所示,若老顶上部岩层的极限跨距小于老顶的极限跨距,当老顶发生破断时,上部岩层失去老顶的支撑作用,其悬露长度大于极限跨距,必然导致上部岩层和老顶一起破断,同时发生破断的顶板层数与极限跨距小于其下位岩层极限跨距的顶板层数相等。因此,当老顶发生破断时,发生工作面初次来压,来压步距即老顶极限跨距,为
(5)
式中:h为老顶厚度;σs为老顶抗拉强度。
这种形式下,采场覆岩的每一层破断都与老顶相似,可利用式(5)计算各层的极限跨距。根据表1数据,计算各岩层极限跨距,结果见表2。

表2 各岩层极限跨距
从表2可看出,2号顶板极限跨距为34.7 m, 1号顶板极限跨距为34.0 m,所以当1号顶板破断时,2号顶板不会发生破断,而且2号顶板之上的岩层由于其支撑作用也不会破断。这与上文分析结果矛盾,因此需对采场覆岩破断模型进行改进。改进模型如图3所示。

图3 改进的采场覆岩破断模型
图3中,老顶初次破断后,其上一层顶板失去老顶的支撑而悬露,但因为该层的极限跨距大于老顶的极限跨距,其悬露长度小于极限跨距,因此,该岩层并不会发生破断,且保持对其上部岩层的支撑作用,使上部岩层不会发生破断。直到老顶再次发生破断,使上层顶板悬露长度急剧增大,超过其极限跨距发生破断(通过分析顶板条件,老顶破断3次上部岩层才破断的情况几乎没有)。这种情况下,工作面的初次来压步距将是老顶前2次垮落步距之和。
工程实际中,可按固支梁模型与悬臂梁模型计算的跨距之和作为初次来压步距,如式(6)所示。可以看出,该情况下来压步距约为式(5)计算结果的1.4倍。
(6)
2.2 周期来压
由于顶板的超前破断规律,当顶板破断后,依旧对下位岩层产生压力,在悬臂梁模型中,可将这种压力看作作用在下位岩层端头的集中力F。建立单个周期来压时老顶第1次破断模型,如图4所示。第2次破断模型如图5所示。

图4 周期来压时覆岩第1次破断模型
设上位岩层容重为γ1,层厚为h1,老顶上位岩层的破断距为l20,则F=γ1h1l20/2。若老顶第1次破断的破断距为l21,第2次破断的破断距为l22,则根据图4和图5可建立方程组:
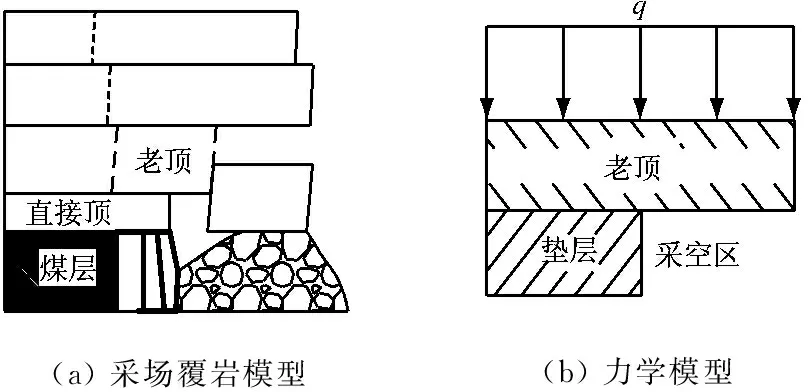
图5 周期来压时覆岩第2次破断模型
(9)
进一步求解可得
可以看出,老顶连续2次垮落步距是不同的,且第2次垮落步距大于第1次。周期来压步距还要根据支架工作阻力做出相应判断。若老顶2次破断时的支架工作阻力都大于来压判据,则老顶2次垮落时工作面都可认为来压,周期来压步距分别为l21和l22;若只有1次垮落时满足来压判据,则老顶破断2次工作面才会来压,周期来压步距为l20。
3 支架工作阻力的确定
回采工作面支架是控制采场矿山压力的基本手段之一。支架的工作阻力是反映顶板运动、围岩控制效果的直观现象,其值受顶板条件、采煤方法、回采工艺及支架性能等的共同作用。在其他条件相同的情况下,支架工作阻力主要与顶板的破断和运移规律有关。
利用前文创建的弹性基础梁模型,可以求出老顶对支架上方直接顶的作用力,加之直接顶本身的重力,即可得到支架的实时工作阻力。直接顶作为弹性基础梁,其对老顶的支撑力p=k0ω。老顶对支架上方直接顶的作用力为
(13)
将式(3)代入式(13)可得
p′=exp(-βc)[(Q0+2βM0)sin (βc)-Q0cos(βc)+Q0exp(βc)]
(14)
设直接顶厚度为h0,容重为γ0,则老顶破断前支架工作阻力为
P=aexp(-βc)[(Q0+2βM0)sin(βc)-Q0cos (βc)+Q0exp(βc)]+ach0γ0
(15)
放顶煤开采情况下,式(15)还要考虑顶煤的重量。
3.1 单个周期内老顶初次破断前支架工作阻力
单个来压周期内老顶初次破断前,老顶除受上部均布载荷作用外,还受到上部破断岩层作用在端点的集中力作用,因此Q0=ql+γ1h1l20/2,M0=ql2/2+γ1h1l20l/2。将其代入式(15),可求得支架实时工作阻力为
(16)
由式(16)可看出,支架工作阻力是关于老顶悬露长度的非线性函数。由于悬露长度是正数,而l>0时,支架工作阻力随老顶悬露长度的增大而增大。当悬露长度达到极限破断距l0时,支架工作阻力达到最大值,发生破断。
将Q0=ql+γ1h1l20/2,M0=ql2/2+γ1h1l20l/2代入式(4),并令l=l21,可求得老顶超前破断距为
(17)
则式(16)中l的取值范围为(0,l21-x1),老顶破断后,支架受力发生改变。如图6所示,单个周期内老顶初次破断后到支架推过破断处期间,支架的工作阻力为
(18)
其中l的取值范围为(l21-x1,l21)。

图6 单个周期内老顶初次破断后支架工作阻力模型
比较式(16)和式(18)可看出,老顶破断后支架工作阻力有一个骤然减小的过程,即除去移架的影响,支架工作阻力曲线将出现一个“山峰状”波动。
3.2 单个周期内老顶二次破断前支架工作阻力
随着工作面继续推进,单个周期内初次破断的老顶掉落采空区,此时式(3)和式(15)中的Q0=q(l-l21),M0=q(l-l21)2/2。将其带入式(4)可求得老顶二次超前破断距为
(19)
由式(15)可求得老顶二次破断前支架工作阻力为
P2=aq(l-l21)exp(-βc)[(βl-βl21+1)×
sin (βc)+exp(βc)-cos (βc)]+acd0γ0
(20)
其中l的取值范围为(l21,l20-x2)。
可以看出,工作阻力随工作面推进也呈二次函数式增大,并且在达到最大值时发生破断。破断后,顶板结构转化成初次破断期间模型,只是在工作面推过破断处前,支架还受到破断的老顶重力作用,如图7所示。

图7 单个周期内老顶二次破断后支架工作阻力模型
在此期间,支架工作阻力为
(21)
其中l的取值范围为(l20-x2,l20)。
可以看出,老顶第二次破断前后支架工作阻力也经历了一次骤然下降的过程,出现了第2个“山峰状”波动。至此支架工作阻力的变化完成一个完整循环。
将采煤工作面有关数据代入式(16)、式(18)、式(20)、式(21),绘制出单个周期内支架工作阻力的变化曲线,如图8所示。求得单个周期内支架工作阻力的平均值为4.77 MN,均方差为0.06 MN。依据来压判据可知,老顶2次破断时都可认为工作面来压,则来压步距分别为5.6,10 m,来压持续长度分别为4.1,3.9 m。

图8 周期来压期间支架实时工作阻力
15201工作面支架阻力实测结果如图9所示,实测周期来压步距为9.1,15.4 m。模型计算结果与实测结果接近。
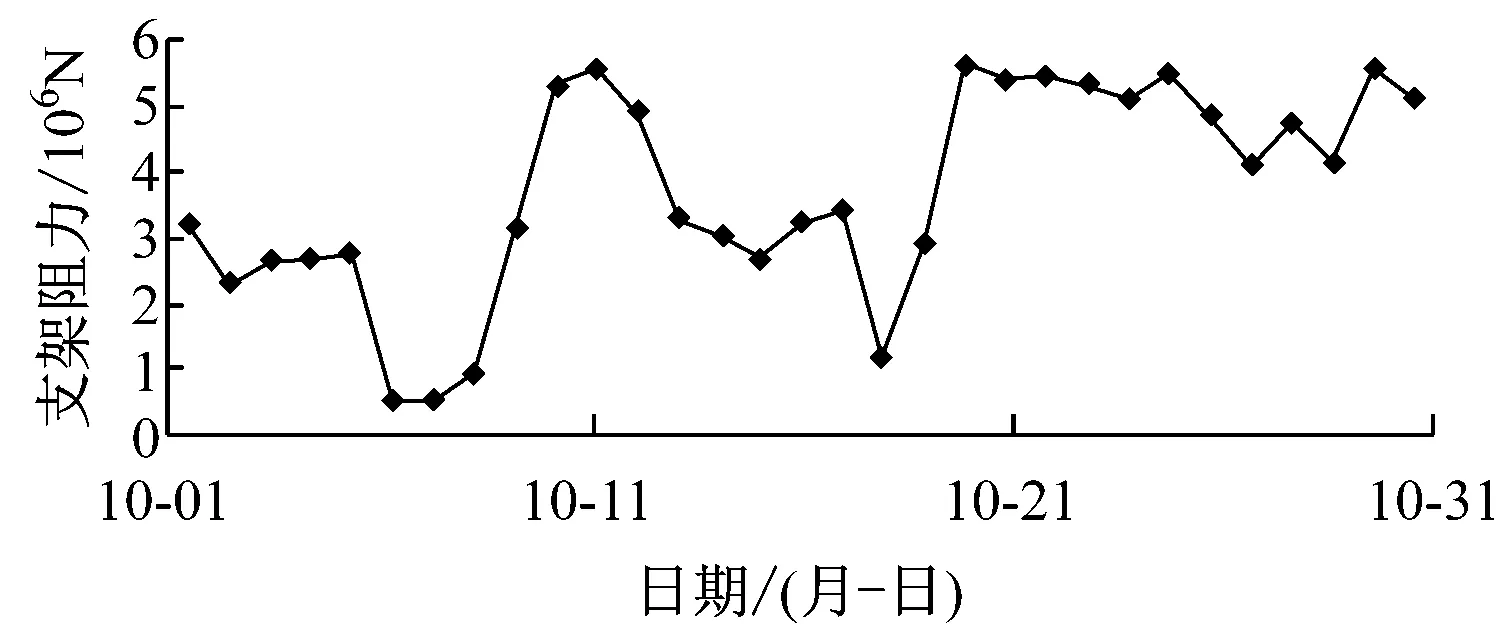
图9 15201工作面支架阻力实测结果
4 结论
(1) 以某煤矿15201综采工作面为工程背景,分析了采场覆岩破断形式。当老顶上位岩层极限跨距大于老顶极限跨距,老顶发生2次破断时,工作面初次来压,初次来压步距为老顶前2次垮落步距之和。
(2) 单个周期来压期间,老顶发生2次垮落,且第2次垮落步距大于第1次。若老顶2次破断时的支架工作阻力都大于来压判据,则老顶2次垮落时工作面都可认为来压;若只有1次垮落时满足来压判据,则老顶破断2次工作面才会来压。
(3) 支架实时工作阻力是关于老顶悬露长度的非线性函数,其随老顶悬露长度的增大而增大。周期来压期间,支架实时工作阻力曲线出现“山峰状”波动。
(4) 将模型计算结果与15201工作面某支架压力实测结果进行对比分析,2种结果接近。但本文模型没有考虑开采强度及断层等地质因素的影响,还需进一步完善。
[1] 屠世浩,袁永.厚煤层大采高综采理论与实践[M].徐州:中国矿业大学出版社,2012.
[2] 王金华.特厚煤层大采高综放开采关键技术[J].煤炭学报,2013,38(12):2089-2098.
[3] 王家臣,王蕾,郭尧.基于顶板与煤壁控制的支架阻力的确定[J].煤炭学报,2014,39(8):1619-1624.
[4] WANG Jiachen,YANG Shengli.A dynamic method to determine the supports capacity in longwall coal mining[J].International Journal of Mining Reclamation and Environment,2014,28(1):277-288.
[5] 杨胜利,王兆会,孔德中,等.大采高采场覆岩破断演化过程及支架阻力的确定[J].采矿与安全工程学报,2016,33(2):199-207.
[6] 史元伟.采煤工作面围岩控制原理和技术[M].徐州:中国矿业大学出版社,2003.
[7] 于雷,闫少宏,刘全明.特厚煤层综放开采支架工作阻力的确定[J].煤炭学报,2012,37(5):737-742.
[8] 王红伟,伍永平,解盘石,等.大倾角特厚煤层综放液压支架工作阻力确定[J].辽宁工程技术大学学报(自然科学版),2014,33(8):1021-1024.
[9] 杜锋,杨本水.KBJ-60Ⅲ-1型数字压力计在单体工作面矿压监测中的应用[J].工矿自动化,2007,33(2):51-52.
[10] 龙驭球.弹性地基梁的计算[M].北京:人民教育出版社,1982:54-64.
[11] 陈杰,杜计平,张卫松,等.矸石充填采煤覆岩移动的弹性地基梁模型分析[J].中国矿业大学学报,2012,41(1):14-19.
[12] 钱鸣高,缪协兴,许家林,等.岩层控制的关键层理论[M].徐州:中国矿业大学出版社,2003:10-14.
[13] 李洪,代进.支撑压力的弹性基础梁解算初探[J].矿山压力与顶板管理,2005(2):4-6.
Determination of real-time working resistance of support infully-mechanized working face of medium-thickness coal seam
CHEN Lei
(School of Resource and Safety Engineering, China University of Mining and Technology(Beijing), Beijing 100083, China)
In order to study evolution of real-time working resistance of hydraulic support with roof breaking in fully-mechanized working face of medium-thickness coal seam, a mechanical model of main roof was established based on elastic foundation beam, and law of main roof movement was analyzed. It was pointed out that breaking position of overlying strata was in front of working face, and analytical solution of pre-breaking distance was given. The roof breaking form of the initial weighting and period weighting of working face were analyzed combined with engineering practice, and calculation formulas of real-time working resistance of support during period weighting were obtained. The research results are as following. Main roof fractures twice in a single weighting cycle. Working resistance of support is a nonlinear function of suspension length of main roof before the first breaking. When the suspension length is equal to limit breaking distance, working resistance of support reaches the maximum value with main roof breaking. Before the second breaking of main roof, working resistance of support increases with working face advance distance as a quadratic function, and reaches the maximum value with main roof breaking.
coal mining; rock control; hydraulic support; working resistance of support; elastic foundation beam; pre-breaking distance; weighting step distance
2016-08-17;
2016-10-19;责任编辑:李明。
高等学校博士学科点专项科研基金资助项目(20120023110023);地质灾害防治与地质环境保护国家重点实验室开放基金资助项目(SKLGP2014K016)。
陈磊(1982-),男,安徽太和人,讲师,博士研究生,现从事矿山压力与岩层控制、煤矿充填开采等方面的研究工作,E-mail:chenlei@cumtb.edu.cn。
1671-251X(2016)12-0036-06
10.13272/j.issn.1671-251x.2016.12.008
TD325
A
时间:2016-12-01 10:27
http://www.cnki.net/kcms/detail/32.1627.TP.20161201.1027.008.html
陈磊.中厚煤层综采工作面支架实时工作阻力确定[J].工矿自动化,2016,42(12):36-41.

